平面直角坐标系新题秀

文/秦丽萍

平面直角坐标系新题秀

文/秦丽萍

平面直角坐标系是研究数与形的重要工具，随着新课程的全面实施，与平面直角坐标系相关的中考题与时俱进，令人耳目一新.现选取几例，供你学习时参考.

一、规律探究型

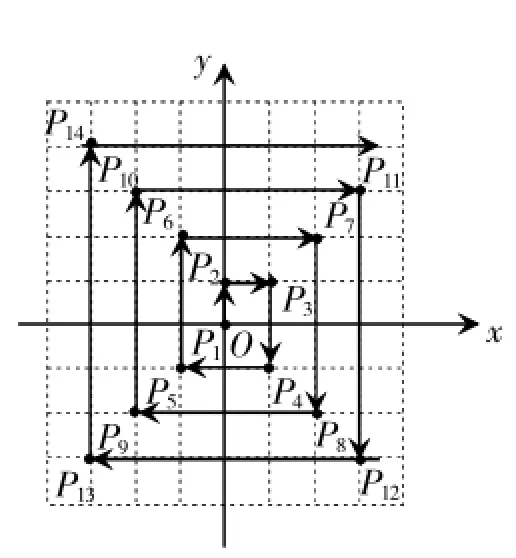
图1

例1（2016年岳阳卷）如图1，在平面直角坐标系中，每个最小方格的边长均为1个单位长，P1，P2，P3，…，均在格点上，其顺序按“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，-1），P5（-1，-1），P6（-1，2），…，根据这个规律，点P2016的坐标为．

分析:根据图象可得，下标为4的倍数的点在第四象限角平分线上，被4除余1的点在第三象限角平分线上，被4除余2的点不在第二象限角平分线上，被4除余3的点在第一象限角平分线上，因此，点P2016在第四象限角平分线上，且横坐标为2016÷4，根据第四象限角平分线上点的特征得出答案．

解：由规律可得，2016÷4=504，∴点P2016在第四象限角平分线上，

∵点P4（1，-1），点P8（2，-2），点P12（3，-3），

∴点P2016（504，-504）.

二、新定义型

例2（2016年常德卷）平面直角坐标系中有两点M（a，b），N（c，d），规定（a，b）⊕（c，d）=（a+c，b+d），则称点Q（a+c，b+d）为M，N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形，则称这个四边形为“和点四边形”，现有点A（2，5），B（-1，3），若以O，A，B，C为顶点的四边形是“和点四边形”，则点C的坐标是．

解：∵以O，A，B，C为顶点的四边形是“和点四边形”，

∴点C的坐标为（2-1，5+3），即填（1，8）．

三、运动变化型

例3（2016年青岛卷）如图2，线段AB经过平移得到线段A′B′，其中点A，B的对应点分别为点A′，B′，这四个点都在格点上．若线段AB上有一个点P（a，b），则点P在A′B′上的对应点P′的坐标为（）

A．（a-2，b+3）．B．（a-2，b-3）．

C．（a+2，b+3）．D．（a+2，b-3）．

解：由图2可得，线段AB向左平移2个单位，向上平移了3个单位，则P′（a-2，b+3）．选A．

图2

图3

四、信息迁移型

例4（2016年北京卷）如图3，在平面直角坐标系中，x轴∥m，y轴∥n，点A（-4，2），点B（2，-4），则坐标原点为（）

A.O1．B.O2．C.O3．D.O4．

解析：A（-4,2），则原点在点A的右边，下方2个单位处，B（2，-4），则原点在点B的左边，上边4个单位处.如图4，O1符合.选A．

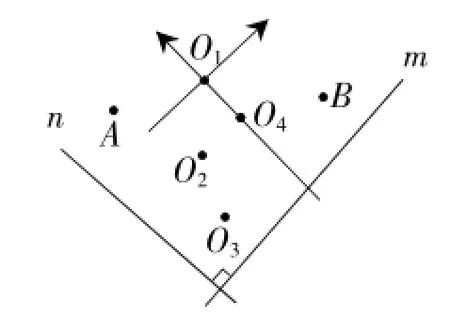
图4

五、实际应用型

例5（2016年山西卷）如图5是利用网格画出的太原市地铁1，2，3号线路部分规划示意图.若双塔西街点的坐标为（0，-1），桃园路点的坐标为（-1，0），则表示太原火车站的点（在网格上）的坐标是．

解：太原火车站的点的坐标是（3，0）．

图5