石墨烯的摩擦力和刚度关系的分子动力学模拟
董 赟 刘晨晗 段早琦 Gueye Birahima 陶 毅张 艳 陈云飞
(1东南大学机械工程学院, 南京 211189)(2兰州理工大学机电工程学院, 兰州 730050)(3东南大学江苏省微纳生物医疗器械设计与制造重点实验室, 南京 211189)
石墨烯的摩擦力和刚度关系的分子动力学模拟
董 赟1,2,3刘晨晗1,3段早琦1,3Gueye Birahima1,3陶 毅1,3张 艳1,3陈云飞1,3
(1东南大学机械工程学院, 南京 211189)(2兰州理工大学机电工程学院, 兰州 730050)(3东南大学江苏省微纳生物医疗器械设计与制造重点实验室, 南京 211189)
采用分子动力学方法建立了基底支撑的多层石墨烯摩擦力模型,统计了不同层数石墨烯在法向载荷作用下的摩擦系数,确立了摩擦力随层数的变化关系;通过针尖吸附薄片所受的范德华力和石墨烯法向变形能与摩擦力的对应关系,得出了法向变形能和界面褶皱势是导致摩擦产生的直接原因,定量分析了界面势垒高度与法向刚度对摩擦力的贡献.结果表明:在不同载荷作用下,3层石墨烯的摩擦系数比1层的摩擦系数高36%、比2层的摩擦系数高40%,1~3层石墨烯的摩擦力均大于范德华力,且随着层数的增加摩擦力与范德华力差值增大;石墨烯层间以刚度串联方式连接,当法向载荷恒定时,3层石墨烯的法向变形能约为2层的1.5倍、1层的3倍,每层石墨烯的变形能对摩擦力的贡献相同,石墨烯摩擦力的产生是层间法向刚度与界面褶皱势刚度共同竞争作用的结果.
分子动力学模拟;石墨烯;势垒高度;法向刚度
摩擦本质上是接触表面原子相互作用下的不可逆能量耗散,涉及复杂的非平衡态热力学过程.石墨烯是一种具有原子级厚度的二维碳材料,具有大比表面积结构,是理想的摩擦力研究材料[1-3].同时由于石墨烯层间较弱的范德华力和较强的层内共价键作用,多层石墨烯可以作为理想的固体润滑剂[4-5].随着原子尺度摩擦理论的发展,人们基于传统Prandtl-Tomlison模型同时结合大量的实验和理论研究得出:当基底为刚体时,界面褶皱势刚度的大小与摩擦力的变化趋势相同[6-7].然而,石墨烯等一般为非刚体,当探针在石墨烯基底上相对滑动时,石墨烯会发生弹性形变,摩擦过程中的黏滑运动是接触表面弹性变形能积累和释放的过程.基于层间弹性对原子尺度摩擦的重要影响,研究摩擦力随法向刚度(层数)的变化规律在纳米摩擦领域引起了广泛关注[8].实验已经证明,法向刚度对摩擦力有非常重要的影响[9].因此,结合界面褶皱势刚度与基底法向刚度的耦合影响是探索原子尺度摩擦产生机理的一种新途径.
目前,关于基底法向刚度和褶皱势刚度对原子尺度摩擦力影响的研究国内外学者得到的结果并不一致.Buldum等[10]最先基于分子动力学以滑块拉动单原子在无限长的弹簧原子链上滑动模拟摩擦力仪的实验过程,分析法向刚度对摩擦力的影响.结果表明,法向载荷不变的条件下,在某一法向刚度区间范围内法向弹性变形对摩擦力有较大影响.Filleter等[11]、Li等[7]和Smolyanitsky等[8]分别就不同层数石墨烯引起的基底法向刚度变化而导致的摩擦力变化进行了理论和实验分析得出:随着层数的增大,法向刚度增大,但摩擦力减小.而Kajita等[12]得出了相反的结果:随着层数的增大,刚度增大,摩擦力增大.Xu等[13]得出另外一种结论:随着层数的增大,刚度减小,摩擦力增大.Zhang等[14]利用MD将单层石墨烯固定在一个弹簧床上,采用改变弹簧床刚度的方法来模拟石墨烯层数的变化,结果表明,随着法向支撑刚度的增大,摩擦力呈指数下降.综上,学者们对法向刚度和界面褶皱势刚度随层数的变化以及摩擦力变化的结论不一致且没有给出统一的理论机理.
摩擦力的产生来源于界面的相对滑动和基底法向变形2部分.本文采用分子动力学方法建立了基底支撑的多层石墨烯摩擦力模型,统计了不同层数石墨烯在法向载荷作用下的摩擦系数,确立了摩擦力随层数的变化关系;通过针尖吸附石墨烯薄片所受的范德华力和多层石墨烯法向变形能与摩擦力的对应关系,定量界面势垒高度与法向刚度对摩擦力的贡献,揭示了法向变形能和界面褶皱势是导致摩擦产生的直接原因和摩擦过程中的能量耗散机制,为构筑纳米摩擦机理提供理论指导.
1 分子动力学模型
本文建立的原子系统包括模拟原子力显微镜(AFM)探针针尖吸附的石墨烯薄片和1~3层的基底支撑多层石墨烯.系统中的支撑体是多层石墨烯的最底层,可以约束其3个方向的位移和速度,因而将最底层设置为支撑刚体.为了模拟AFM探针的扫描过程,将模拟针尖吸附的石墨烯薄片用弹簧连接于外界的滑块(以恒速v=3 m/s滑动),探针滑动方向为锯齿形(zigzag)方向.多层石墨烯以AB方式堆垛,尺寸大小为10.3 nm×10.3 nm(4 032个原子),层间距离为0.335 nm.针尖吸附薄片的尺寸为2.6 nm×2.6 nm(264个原子).将基底Y方向设置成周期性边界条件,X方向最外行原子为固定边,次外行原子为调温边,探针沿X方向滑动.模型如图1所示.
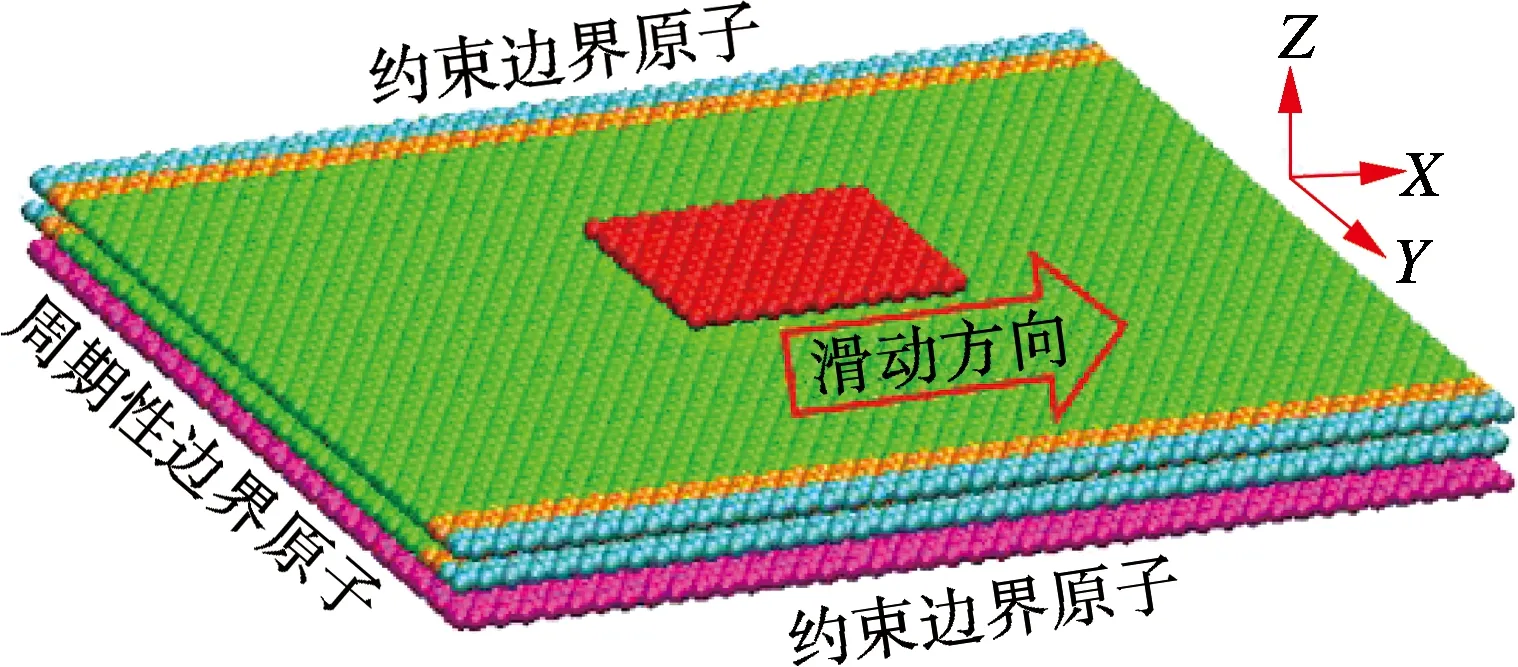
图1 基底支撑的两层石墨烯模型
模型模拟薄片在无限长的多层石墨烯基底上滑动,同层原子之间的作用势采用Tersoff-Brenner势,夹层原子之间的作用势采用耦合强度较弱的Lennard-Jones势,势阱常数为3.73 meV,平衡常数为0.34 nm,截断半径为0.884 nm.模拟力控制接触模式的AFM扫描过程,用反馈信息调整针尖吸附薄片在Z方向的位置,在确保法向载荷恒定的同时尽量减小针尖吸附薄片的振荡.本文所有计算都是在0.5 ns内完成的,系统采用Langevin调温法,温度为300 K,所有的模拟都是通过LAMMPS软件包[15]实现.
2 石墨烯摩擦力-法向及界面刚度
2.1 摩擦力与层厚的关系
采用分子动力学模型,分别对不同层数的石墨烯施加96~288 nN的法向载荷,并通过摩擦力黏滑曲线计算出平均摩擦力,得到摩擦力-法向载荷对应拟合曲线,如图2所示.摩擦系数表示为
(1)
式中,Ffave为平均摩擦力;Fc为法向面载荷.
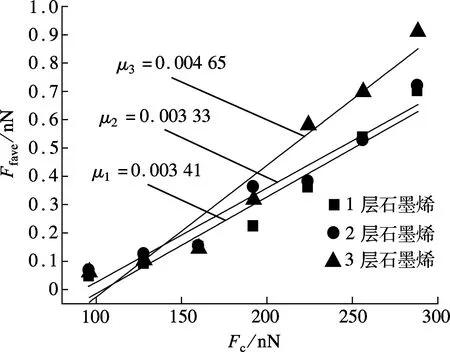
图2 不同层数摩擦系数
模拟结果表明,1层和2层石墨烯的摩擦系数变化不大,而3层的摩擦系数比1层的摩擦系数增加了36%,比2层增加了40%.2层石墨烯的摩擦系数μ=0.003 33与实验结果μ=0.03[16]相差不大,引起差异的原因可能是样品尺寸、扫描速度以及约束方式的不同.
对3层石墨烯上的探针吸附薄片施加Z方向288 nN的接触面载荷,观察其黏滑行为.滑块和探针吸附薄片之间的所有弹簧力总和等于摩擦力Ff,同时计算出探针吸附薄片和基底之间X方向的范德华力Fvx,得出滑动位移-力曲线,如图3所示.

图3 三层石墨烯的黏滑曲线

2.2 摩擦力与界面褶皱势的关系
针尖吸附薄片在滑动过程中受到基底各层原子对其产生的范德华力作用而耗散能量,这是因为2个分子之间的作用力是短程力,远离针尖的石墨烯对针尖吸附薄片的作用力很小.因此可以认为针尖吸附薄片与基底之间的范德华力仅反映由顶层石墨烯界面势垒高度引起的作用力.分别统计不同层数不同法向载荷作用下的范德华力和摩擦力,定量确定势垒高度对摩擦力的影响,如图4所示.
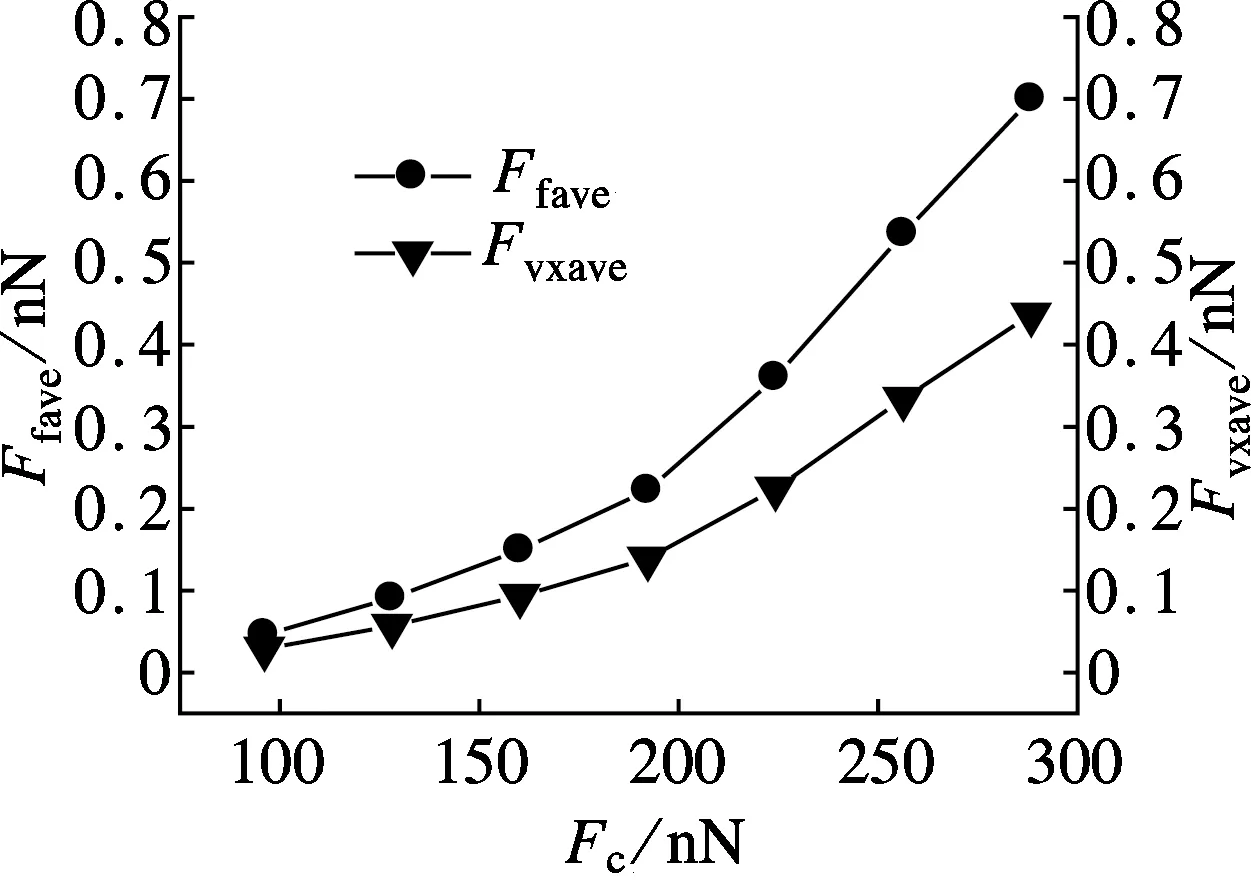
(a) 1层石墨烯

(b) 2层石墨烯

(c) 3层石墨烯
由模拟结果可以看出,摩擦力和范德华力都随法向载荷单调增大.随着法向载荷的增大,原子之间的嵌入深度趋于饱和,导致势垒高度变大,需要更大的外力作用才能使原子克服势垒的阻碍,这将会引起更多的摩擦能耗.因此,反应界面势垒高度的范德华力是引起摩擦力的重要原因.与摩擦系数相同,当法向载荷相同时,反映界面褶皱势强弱的范德华力在1层和2层石墨烯变化不明显,3层石墨烯显著变大.当2层石墨烯在法向载荷为192 nN时,出现摩擦力和范德华力突变增大,造成这种现象的原因可能是此时滑移状态发生变化,增大了单位滑移长度的能量耗散(耗散率),导致摩擦能耗增大,摩擦力曲线出现凸峰.
石墨烯层数不同会引起法向刚度变化,导致法向变形能有所差异,因此定量法向刚度对摩擦力的影响也很关键.
2.3 摩擦力与法向刚度的关系
以AFM为物理模型,当计算探针吸附薄片压入区域的深度时,将基底顶层石墨烯针尖吸附薄片正下方与薄片大小相同的264个原子作为压入区域(见图1),统计不同法向载荷作用下压入区域质心原子的法向位移.由于石墨烯为非刚体,探针吸附薄片在基底表面扫描过程中引起薄片前端的表面区域产生褶皱,实际上增大了薄片和基底之间的接触面积.统计每个原子在不同法向载荷Fc作用下顶层石墨烯压入区的压入深度δ,建立法向载荷-深度的曲线,如图5所示.
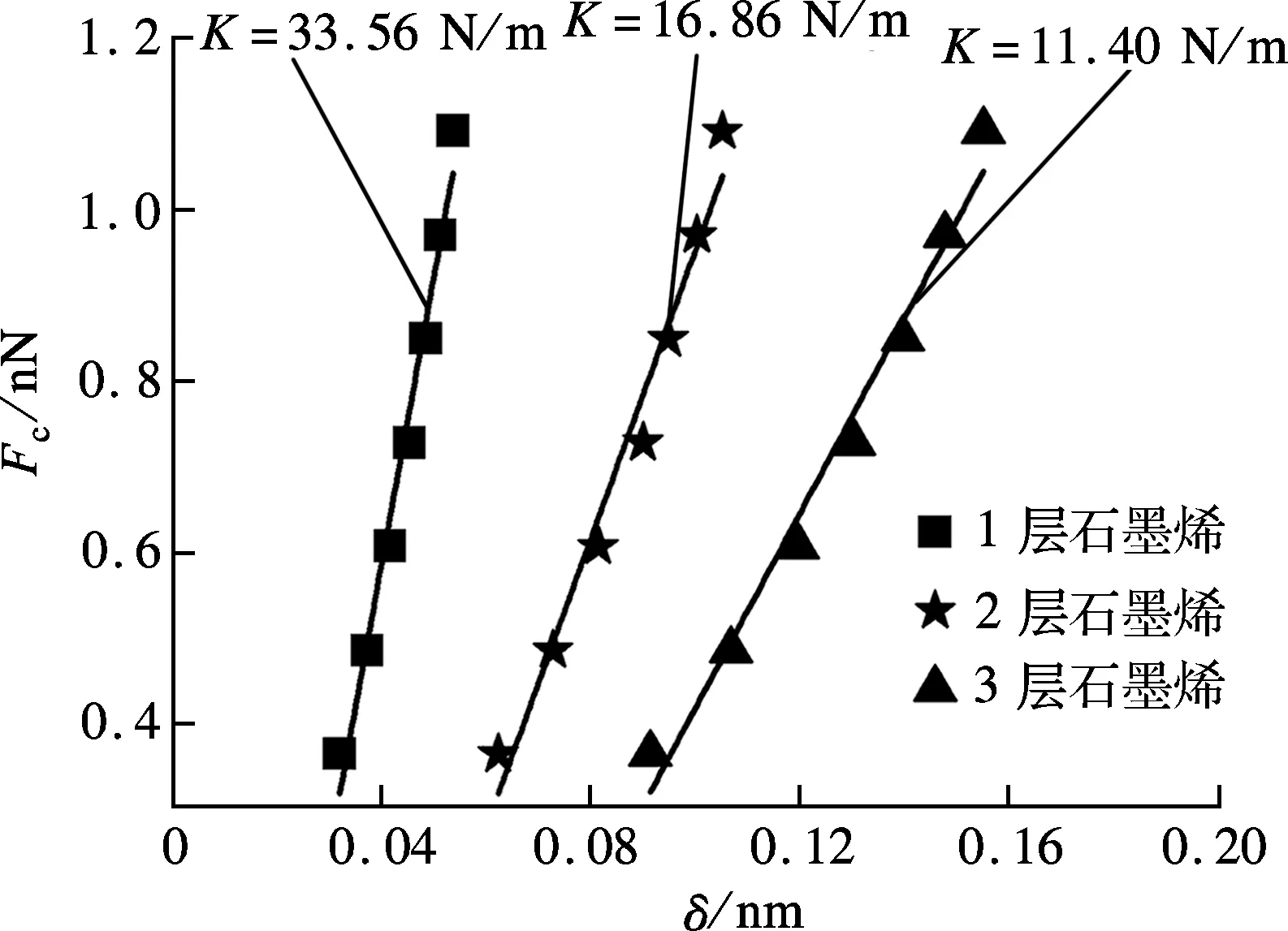
图5 不同层数的法向载荷-压入深度曲线
从图中可以看出,相同载荷作用下,层数越大,压入深度越深,这表明其法向刚度越小.根据下式计算出不同层数石墨烯单原子的法向刚度:
(2)
计算结果表明,法向刚度随着层数的增大呈线性递减.这是因为石墨烯层间以刚度串联方式连接,总刚度K满足
(3)
式中,Ki为第i-1与第i层之间的法向刚度,且为恒值;n为石墨烯层数.这与文献[13]的规律完全吻合.而法向刚度不同时引起的变形能也不同,从而对摩擦力的贡献也不同.利用文献[8]中的假设,变形能为
(4)
统计出不同法向载荷作用下顶层石墨烯压入区的变形能,如图6所示.
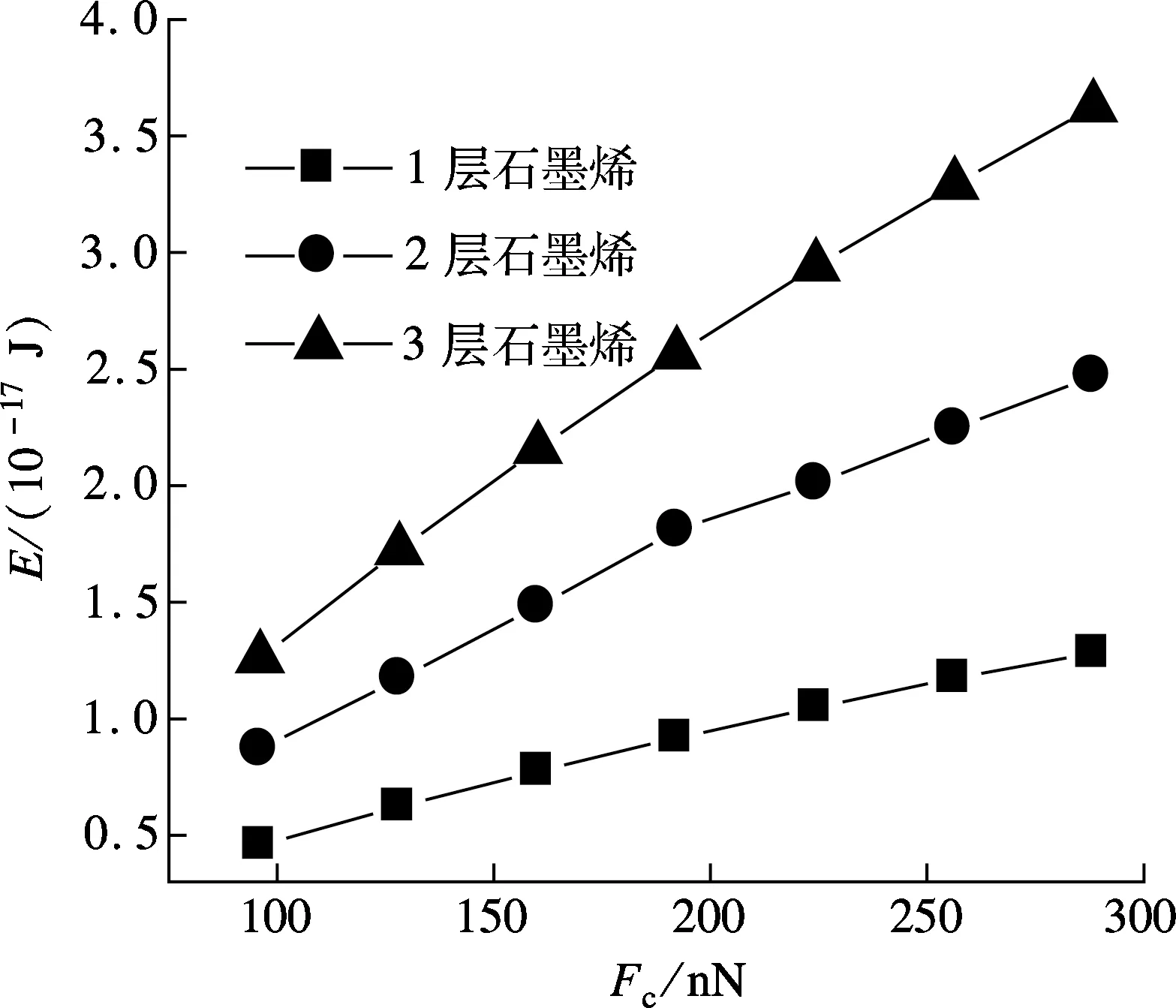
图6 不同层数的法向变形能
从图中可以看出,相同法向载荷作用下变形能随着层数的增大几乎成倍数增大,并且层数相同时,法向变形能随着法向载荷的增大呈线性增大.如当法向载荷Fc=288 nN时,3层石墨烯的法向变形能为 3.63×10-17J,约为1层时 1.28×10-17J 的3倍,2层石墨烯的法向变形能为 2.47×10-17J,约为1层时的2倍,可以认为,每层石墨烯对变形能的贡献相同.变形能越大,在滑动过程中耗散的能量越大,产生的摩擦越大.
不同层数法向载荷对应的摩擦力与范德华力的差值Fe(见图7)并不完全与法向变形能相对应.导致这种结果的原因可能是,石墨烯层数的增加改变了法向方向声子耗散的模态和主导频率,造成单层石墨烯要比2层和3层石墨烯的摩擦声子耗散速率快,这种耗散速率的不同抵消了法向变形能对摩擦力的贡献,造成1层和2层石墨烯的摩擦力和范德华力几乎相等,3层石墨烯的摩擦力和范德华力并不是1层的3倍.
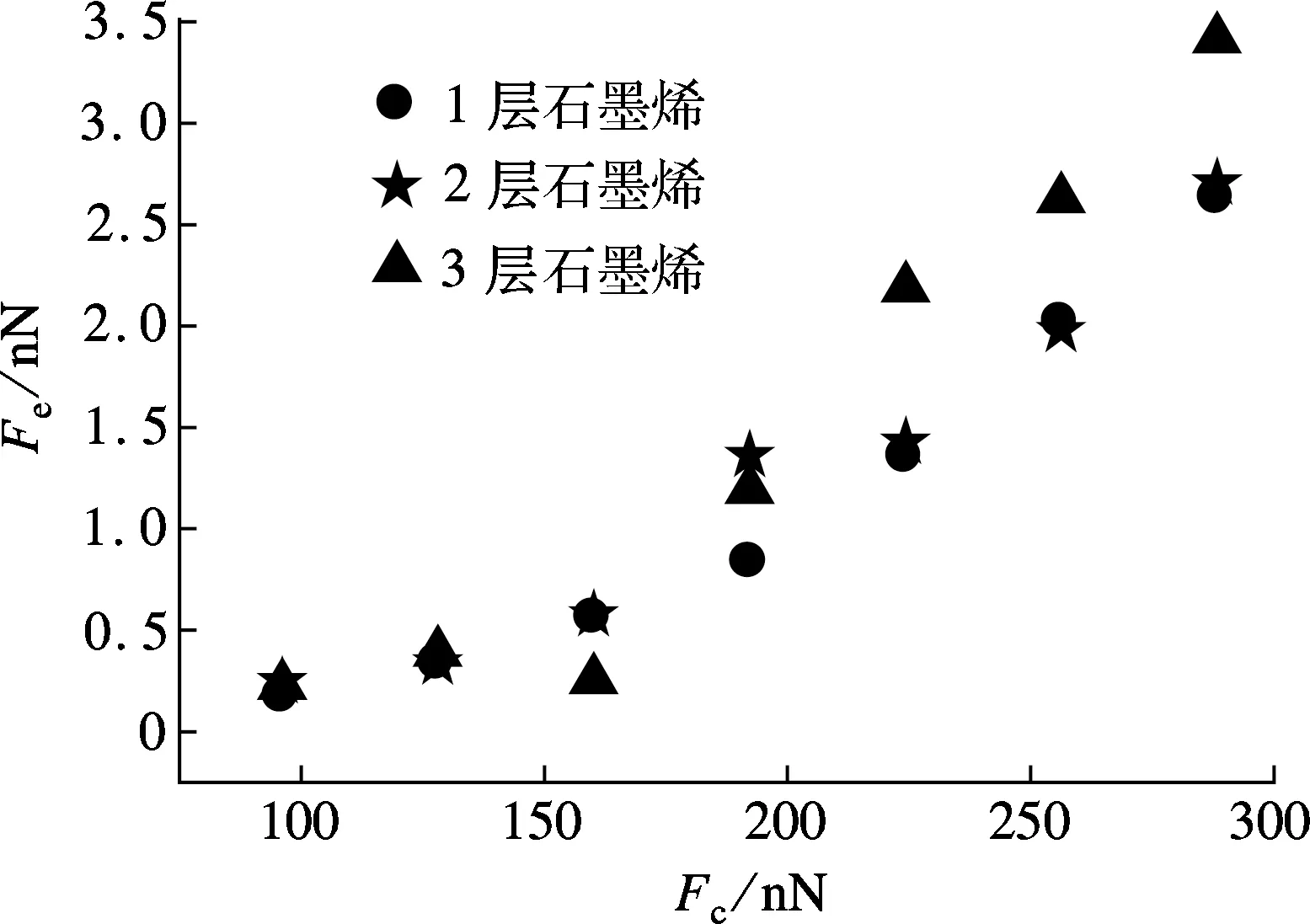
图7 摩擦力与范德华力差值
随着法向刚度的增大,变形能逐渐减小,界面原子之间的相互嵌入作用趋于平缓,嵌入能增大率降低,势垒高度趋于平稳,由界面刚度引起的摩擦力接近极限值;当法向刚度增大到基底接近刚体时,界面原子的嵌入能达到饱和,势垒高度不变,此时由界面刚度贡献的摩擦力达到定值,而法向刚度引起的变形能趋于零.因此,石墨烯摩擦力的产生是层间法向刚度与界面褶皱势刚度共同竞争作用的结果.
3 结语
采用分子动力学方法建立了基底支撑的多层石墨烯摩擦力模型,统计了不同层数石墨烯在法向载荷作用下的摩擦系数,建立了摩擦力随层数的变化关系;通过计算法向变形能和针尖吸附薄片所受的范德华力与摩擦力的对应关系,得出了法向变形能和界面褶皱势是导致摩擦产生的直接原因.研究结果表明,在不同载荷作用下,3层石墨烯的摩擦系数明显高于1层和2层,1~3层石墨烯的摩擦力均大于范德华力,且随着层数的增加摩擦力与范德华力差值越大;石墨烯层间以刚度串联方式连接,当法向载荷恒定时,3层石墨烯的法向变形能约为2层的1.5倍、1层的3倍,每层石墨烯的变形能对摩擦力的贡献相同,石墨烯摩擦力的产生是由层间法向刚度与界面褶皱势刚度共同竞争作用的结果.本文揭示了摩擦过程中的能量耗散机制,为构筑纳米摩擦能量耗散机理提供理论指导.
References)
[1]Geim A K. Graphene: Status and prospects [J].Science, 2009, 324(5934): 1530-1534. DOI:10.1126/science.1158877.
[2]Chang T, Zhang H, Guo Z, et al. Nanoscale directional motion towards regions of stiffness [J].PhysicalReviewLetters, 2015, 114(1): 015504-1-015504-5. DOI:10.1103/PhysRevLett.114.015504.
[3]Yang J, Liu Z, Grey F, et al. Observation of high-speed microscale superlubricity in graphite [J].PhysicalReviewLetters, 2013, 110(25): 255504-1-255504-5. DOI:10.1103/PhysRevLett.110.255504.
[4]Kim K S, Lee H J, Lee C, et al. Chemical vapor deposition-grown graphene: The thinnest solid lubricant [J].ACSNano, 2011, 5(6): 5107-5114. DOI:10.1021/nn2011865.
[5]Berman D, Erdemir A, Sumant A V. Graphene: A new emerging lubricant [J].MaterialsToday, 2014, 17(1): 31-42. DOI:10.1016/j.mattod.2013.12.003.
[6]Wang Z J, Ma T B, Hu Y Z, et al. Energy dissipation of atomic-scale friction based on one-dimensional Prandtl-Tomlinson model [J].Friction, 2015, 3(2): 170-182. DOI:10.1007/s40544-015-0086-2.
[7]Li Q, Lee C, Carpick R W, et al. Substrate effect on thickness-dependent friction on graphene [J].PhysicaStatusSolidiB, 2010, 247(11/12): 2909-2914. DOI:10.1002/pssb.201000555.
[8]Smolyanitsky A, Killgore J P, Tewary V K. Effect of elastic deformation on frictional properties of few-layer graphene [J].PhysicalReviewB, 2012, 85(3): 035412-1-035412-6. DOI:10.1103/physrevb.85.035412.
[9]Lee C, Li Q, Kalb W, et al. Frictional characteristics of atomically thin sheets [J].Science, 2010, 328(5974): 76-80. DOI:10.1126/science.1184167.
[10]Buldum A, Ciraci S. Atomic-scale study of dry sliding friction [J].PhysicalReviewB, 1997, 55(4): 2606-2611. DOI:10.1103/physrevb.55.2606.
[11]Filleter T, McChesney J L, Bostwick A, et al. Friction and dissipation in epitaxial graphene films [J].PhysicalReviewLetters, 2009, 102(8): 086102-1-086102-4. DOI:10.1103/PhysRevLett.102.086102.
[12]Kajita S, Washizu H, Ohmori T. Deep bulk atoms in a solid cause friction [J].EurophysicsLetters, 2009, 87(6): 66002-1-66002-5. DOI:10.1209/0295-5075/87/66002.
[13]Xu L, Ma T B, Hu Y Z. et al. Vanishing stick-slip friction in few-layer graphenes: The thickness effect [J].Nanotechnology, 2011, 22(28): 285708-1-285708-6. DOI:10.1088/0957-4484/22/28/285708.
[14]Zhang H, Guo Z, Gao H, et al. Stiffness-dependent interlayer friction of graphene [J].Carbon, 2015, 94: 60-66. DOI:10.1016/j.carbon.2015.06.024.
[15]Plimpton S. Fast parallel algorithms for short-range molecular dynamics [J].JournalofComputationalPhysics, 1995, 117(1): 1-19. DOI:10.1006/jcph.1995.1039.
[16]Shin Y J, Stromberg R, Nay R, et al. Frictional characteristics of exfoliated and epitaxial graphene [J].Carbon, 2011, 49(12): 4070-4073. DOI:10.1016/j.carbon.2011.05.046.
Molecular dynamics simulations of stiffness-dependent friction of graphene
Dong Yun1,2,3Liu Chenhan1,3Duan Zaoqi1,3Gueye Birahima1,3Tao Yi1,3Zhang Yan1,3Chen Yunfei1,3
(1School of Mechanical Engineering, Southeast University, Nanjing 211189, China) (2School of Mechanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China) (3Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments, Southeast University, Nanjing 211189, China)
Based on molecular dynamics simulations,a supported multilayer graphene friction model was constructed. First, the statistics on the friction coefficient of graphene with different layers under normal loads was carried out, and the relationship between the friction and layer numbers was obtained. Then the contributions of van der Waals force of the tip and the elastic deformation on the top layer of the multilayer graphene substrate on the friction force were analyzed. Finally, it was demonstrated that the effects on normal deformation energy and surface compliance were directly related to the observed friction force, and the contributions of surface energy barrier height and normal stiffness on the friction were quantitatively analyzed . The results indicate that under different loads the friction coefficient of 3 layers is 36% higher than that of 1 layer, and 40% higher than that of 2 layers; all friction forces are greater than van der Waals forces and the difference value between them becomes larger with the numbers of layers increasing; when the normal load is constant, the elastic energy of 3 layers is about 1.5 times as much as that of 2 layers and threefold of that of 1 layer, that is, the elastic energy of each layer has equal contribution to the friction due to the stiffness between layers is in series, the friction of graphene is caused by the competition between the stiffnesses of normal deformation energy and surface compliance.
molecular dynamics simulations; graphene; energy barrier; surface compliance

第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.006
2016-06-16. 作者简介: 董赟(1984—),男,博士生;陈云飞(联系人),男,博士,教授,博士生导师,yunfeichen@seu.edu.cn.
国家自然科学基金资助项目(51665030,51435003,51575104).
董赟,刘晨晗,段早琦,等.石墨烯的摩擦力和刚度关系的分子动力学模拟[J].东南大学学报(自然科学版),2017,47(1):28-32.
10.3969/j.issn.1001-0505.2017.01.006.
O484.2
A
1001-0505(2017)01-0028-05

