基于译码可靠性的系统Polar码删余方法
赵生妹 邵珠要 陈汉武
(1南京邮电大学通信与信息工程学院, 南京 210003)(2东南大学计算机科学与工程学院, 南京 210096)
基于译码可靠性的系统Polar码删余方法
赵生妹1邵珠要1陈汉武2
(1南京邮电大学通信与信息工程学院, 南京 210003)(2东南大学计算机科学与工程学院, 南京 210096)
为了研究删余系统Polar码的性能,提出了一种基于译码可靠性的系统Polar码删余方法.考虑到信道噪声对不同码字比特译码结果的影响并不相同,通过高斯近似的方法计算码字中每个比特的译码可靠性值并对其排序,选择可靠性值较低的码字比特位置作为删余位,构造删余系统Polar码.分析了不同删余方法对误比特率(BER)性能的影响,并将系统Polar码与非系统Polar码的性能进行了对比.仿真结果表明:在同等删余码率下,基于译码可靠性删余法的Polar码性能优于随机删余法的Polar码性能;与等条件下非系统Polar码相比,基于译码可靠性删余法的系统Polar码具有更好的误比特率性能.
删余;译码可靠性;系统Polar码;高斯近似
Polar码是由Arikan[1]提出的一种新型信道编码方法.基于信道极化理论,Polar码已被证明能够达到对称二进制离散无记忆信道的信道容量.它是至今为止理论上唯一可达到香农限的信道编码方法,而且是一种具有低复杂度的编译码方法.自提出以来,Polar码引起了人们极大的关注[2-4].文献[5]通过设计不同的巴氏参数对各种信道下Polar码的性能进行了分析,并给出了不同信道下Polar码的构造方案.文献[6]将Polar码应用到纠错延后量子秘钥协商协议中,通过信道编码完成纠错过程,提高了协商协议的可靠性和安全性.此外,Polar码在编码调制系统中也发挥着重要的作用[7-8].
通信系统的结构并不需要因为码字的删余而改变,因此,通常将删余方法用于通信系统中以实现时变信道的码率兼容.发送端先根据最差信道环境的要求,构造一个低码率的纠错码字(如s位);然后根据时变信道特性需求和选择的删余方法确定码字中的删余位置(如t位),删除部分比特,删余后码字的码长为s-t;随后,将码长为s-t的删余后码字在信道中传输.在接收端,首先将接收码s-t位按删余位置补零方法,获得长度为s的接收码,然后根据译码算法对补零后的接收码进行译码,获得发送信息.由于能够使用相同的发射机、接收器实现不同码率的通信,删余操作在满足无线信道时变特性要求的同时,大大降低了发射机的复杂度,提高了传输效率.
删余的位置影响着删余后码字的性能,即不同的删余方法具有不同的性能.针对Polar码,学者们已经提出了一些删余方法.例如,Eslami等[9]提出了随机删余法和截止树删余法.随机删余法是在码字中随机地选择删余位置;截止树删余法则是通过计算每个码字比特在截止树中出现的次数,将出现次数较少的码字比特作为删余位置.文献[10]分析了这2种删余方法在不同信道下删余Polar码的性能以及在图像传输中的应用.
Polar码可分为系统Polar码和非系统Polar码.与非系统Polar码相比,系统Polar码具有更好的误比特率性能[11],且信息比特位置可以在系统码中显著表现出来.
本文提出了一种基于译码可靠性的系统Polar码删余方法.首先,通过高斯近似的方法[12-13]计算出每个系统码字比特的译码可靠性;然后,将码字比特的译码可靠性进行排序,选择译码可靠性较低的码字比特作为删余位置,构造出删余系统Polar码,并且比较和分析基于译码可靠性删余法的系统Polar码的性能.
1 系统Polar码
标准形式下的Polar码为非系统码.对于长度为N的Polar码,其编码过程可表示为
x=uGN
(1)

信息序列u包含信息位和冻结位.若集合A为集合{1,2,…,N}中的一个子集,且A和Ac分别表示信息位和冻结位的集合,则u=[uAuAc],式(1)可改写为
x=uAGA+uAcGAc
(2)
式中,GA和GAc为GN的子矩阵,分别由GN中信息位和冻结位所在的行向量构成.
在系统Polar码[11,14]中,编码后的码字x被分成2个部分,即x=[xBxBc],其中B为集合{1,2,…,N}中的一个子集,Bc为B的补集.式(2)可改写为
xB=uAGAB+uAcGAcB
(3)
xBc=uAGABc+uAcGAcBc
(4)
式中,GAB,GABc,GAcB,GAcBc均为GN的子矩阵.
系统Polar码中,信息位被直接映射到码字中,信息比特明显可见.与非系统Polar码中uA类似,xB为用户数据,uAc为非系统Polar码中的冻结位比特.式(3)和(4)在uA和xB可能的取值之间建立了一一对应关系.因此,给定一个用参数(A,uAc)表示的非系统Polar码编码,系统Polar码的编码便可以用参数(B,uAc)来表示.
若定义生成矩阵形式为GN=F⊗n,则GN是可逆的,且GN的任意子矩阵也是可逆的.为了建立xB和uA之间的一一对应关系,并且保证GAB是可逆的,系统Polar码中可以通过令B=A来完成信息比特集合的选取.因此,式(3)和(4)可写为
xA=uAGAA+uAcGAcA
(5)
xAc=uAGAAc+uAcGAcAc
(6)
其中,GAA,GAcA,GAAc,GAcAc均为GN的子矩阵.
由此可知,当Polar码经过系统形式的编码操作后,信息比特能够被明显地区分出来.
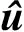
(7)
2 基于译码可靠性的删余方法
以码长为8的Polar码为例,基于译码可靠性的Polar码删余模型如图1所示.图中,u1~u4为输入的信息比特;x1~x8为编码后的码字比特;p1~p8为每个码字比特对应的可靠性值.

图1 基于译码可靠性的Polar码删余模型
首先对输入的信息序列进行编码,然后依据计算出来的码字比特的译码可靠性值大小对码字比特进行排序,根据删余码率确定删余位数,将可靠性值较低的位置选作删余位,对编码比特进行删余,仅对删余后剩余的码字进行传输.

(8)
(9)

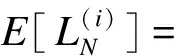
(10)
式中,φ(x)的表达式为[15]
φ(x)
(11)

(12)

(13)
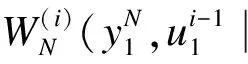
下面将提出的基于译码可靠性的删余方法应用在系统Polar码中,构造删余系统Polar码.生成矩阵的形式为GN=F⊗n,系统码中的信息比特集合B对应信息序列u中信息位的集合A,集合Bc对应冻结位集合Ac.计算出各比特信道的译码可靠性值并确定删余位数后,删余位集合包含于集合Bc中,只需将码字x中对应可靠性值较低的位删除即可得到删余后的码字.
图2为基于译码可靠性删余法的系统Polar码传输系统框图.基于译码可靠性的系统Polar码删余方法的详细步骤如下:
① 采用高斯近似的方法计算出每个比特信道的错误概率,进而计算出每个比特信道的可靠性值,并对可靠性值进行排序.
② 将可靠性值较高的比特信道位置选作信息位集合A,将可靠性值较低的位置作为冻结位集合Ac,以此构造母码.
③ 将信息序列u送入编码器,采用系统Polar码的编码方法进行编码,其中B=A,并提取出xB.
④ 令初始化长度为N的向量p={p1,p2,…,pN}为零向量,根据设计的删余码率计算出删余位数m,将计算出的可靠性值最低的m位对应于p中的位置设置为1.
⑤ 对码字x进行删余,删除的码字为{xi:pi=1},其中xi为x中第i个码字比特.
⑥ 删除的码字不经信道传输,仅传输剩余码字.
⑦ 在接收端,将删余位置的信息补充完整,即将删余位置的似然比赋值为1.

图2 基于译码可靠性删余法的系统Polar码传输系统框图
3 仿真及性能分析
本文通过数值仿真来分析基于译码可靠性删余法的系统Polar码性能.选取的母码码长N=1 024,码率为0.5,在此基础上构造删余系统Polar码.采用高斯近似的方法计算每个比特信道的译码可靠性值,编码比特删余位置的选择取决于其对应可靠性值的大小.仿真时,将删余码率a分别选取为0.6,0.7,0.8,并将这3种删余码率下的仿真性能进行了对比.同时,在每一种删余码率下,将随机删余法与基于译码可靠性删余法进行对比,并将基于译码可靠性删余法下的系统Polar码与非系统Polar码的性能进行了对比.仿真时,最大帧数设为1×104.
图3给出了码长为1 024、信噪比为1 dB时各比特信道的可靠性值.由图可知,各比特信道的可靠性值不同.实际过程中,选取可靠性值较低的512位比特信道编号作为冻结位集合,剩下可靠性值较高的512位比特信道编号作为信息位集合.进行删余时,依据可靠性值从低到高的顺序将码字中相应位删除.当a=0.6时,编码比特中需删余的位数为1 024-512/0.6=171.同理,a=0.7,0.8时对应的删余位数分别为293和384.
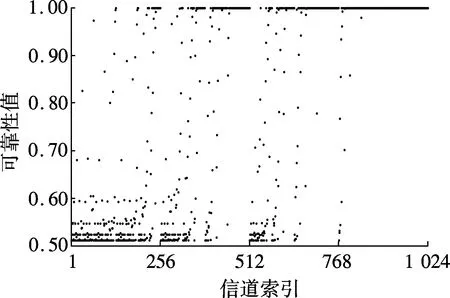
图3 各比特信道的可靠性值
图4给出了a=0.6,0.7,0.8时误比特率随信噪比变化曲线.当a=0.6时,随机删余法的误比特率要比基于译码可靠性删余法的误比特率高,且信噪比越大,二者的差距越明显,当信噪比达到5 dB时,基于译码可靠性删余法的Polar码的误比特率已降到10-4.同时,系统Polar码的性能明显优于非系统Polar码.当信噪比为5 dB时,系统Polar码的误比特率达到10-5,而当信噪比达到6 dB时,系统码的误比特率接近10-7.
当a=0.7,0.8时,相比随机删余法和可靠性删余法下的非系统Polar码,基于译码可靠性删余法的系统Polar码性能更优越.删余码率的提高增加了译码过程中的不确定性,导致误比特率增大,但与非系统Polar码相比,系统Polar码仍具有较低的误比特率.考虑到系统Polar码的构造方法,系统Polar码在抑制误差传播方面具有更好的鲁棒性.因此,将基于译码可靠性的删余方法应用在系统Polar码中所构造的删余系统Polar码可以获得良好的性能.

图4 误比特率随信噪比变化曲线
4 结语
本文提出了一种基于译码可靠性的系统Polar码删余方法.首先利用高斯近似的方法计算出每个码字比特的译码可靠性,删除可靠性值较低的码字比特,构造出删余系统Polar码;然后,分析该删余系统Polar码在高斯信道下的误比特率性能.同时,对基于译码可靠性的删余法和随机删余法下的非系统Polar码性能进行了仿真.研究结果表明,基于译码可靠性删余法优于随机删余法;基于译码可靠性删余法的系统Polar码的性能明显优于非系统Polar码.因此,基于译码可靠性删余法的系统Polar码具有良好的性能,可在实现码率兼容的同时,保证较低的误比特率.
References)
[1]Arikan E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels [J].IEEETransactionsonInformationTheory, 2009, 55(7): 3051-3073. DOI:10.1109/tit.2009.2021379.
[2]Zhang Y X, Liu A J, Pan K G, et al. A practical construction method for polar codes [J].IEEECommunicationsLetters, 2014, 18(11): 1871-1874. DOI:10.1109/lcomm.2014.2358228.
[3]Miloslavskaya V. Shortened polar codes [J].IEEETransactionsonInformationTheory, 2015, 61(9): 4852-4865. DOI:10.1109/TIT.2015.2453312.
[4]钱凯, 赵生妹, 施鹏. 高斯窃听信道中删余Polar码的设计方法研究[J]. 信号处理, 2014, 30(11): 1345-1348. Qian Kai, Zhao Shengmei, Shi Peng. Design of the Gaussian wiretap channel with punctured polar codes [J].JournalofSignalProcessing, 2014, 30(11): 1345-1358. (in Chinese)
[5]Zhao S M, Shi P, Wang B. Designs of Bhattacharyya parameter in the construction of polar codes[C]//2011 7thInternationalConferenceonWirelessCommunications,NetworkingandMobileComputing. Wuhan,China, 2011: 1-4. DOI:10.1109/wicom.2011.6040179.
[6]肖红, 施鹏, 赵生妹. 基于Polar码的纠错延后量子协商协议[J]. 中国科学:科学技术, 2015, 45(8): 843-848. Xiao Hong, Shi Peng, Zhao Shengmei. A reconciliation protocol with delayed error correction for quantum key distribution[J].ScientaiSinicaTechologica, 2015, 45(8): 843-848.(in Chinese)
[7]陈贤卿. 高效调制通信系统中的检测与信道编码研究[D]. 南京:东南大学信息科学与工程学院, 2012.
[8]樊婷婷, 杨维, 许昌龙. 基于Polar码的BICM系统在AWGN信道中的性能[J]. 东南大学学报(自然科学版), 2016, 46(1): 18-22. Fan Tingting, Yang Wei, Xu Changlong. Performance of BICM system based on polar code in AWGN channel[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016, 46(1): 18-22. (in Chinese)
[9]Eslami A, Pishro-Nik H. A practical approach to polar codes [C]//2011IEEEInternationalSymposiumonInformationTheoryProceedings. St.Petersburg,Russia, 2011: 16-20. DOI:10.1109/isit.2011.6033837.
[10]施鹏. 删余Polar码及其在纠错延后协商协议和图像传输中的应用研究[D]. 南京: 南京邮电大学通信与信息工程学院, 2014.
[11]Arikan E. Systematic polar coding [J].IEEECommunicationsLetters, 2011, 15(8): 860-862. DOI:10.1109/lcomm.2011.061611.110862.
[12]Li H J, Yuan J H. A practical construction method for polar codes in AWGN channels [C]//2013IEEETENCONSpringConference. Sydney, Australia, 2013: 223-226. DOI:10.1109/tenconspring.2013.6584444.
[13]Wu D, Li Y, Sun Y. Construction and block rate analysis of polar codes over AWGN channel based on Gaussian approximation [J].IEEECommunicationLetters, 2014, 18(7): 1099-1102. DOI:10.1109/lcomm.2014.2325811.
[14]Vangala H, Hong Y, Viterbo E. Efficient algorithms for systematic polar encoding [J].IEEECommunicationsLetters, 2016, 20(1): 17-20.DOI:10.1109/lcomm.2015.2497220.
[15]Zhang Z, Zhang L, Wang X. A split-reduced successive cancellation list decoder for polar codes [J].IEEECommunicationsLetters, 2016, 34(2): 292-302.
Puncturing method for systematic Polar code based on decoding reliability
Zhao Shengmei1Shao Zhuyao1Chen Hanwu2
(1College of Telecommunications and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China) (2School of Computer Science and Engineering, Southeast University, Nanjing 210096, China)
To study the performance of the punctured systematic Polar code, a puncturing method for the systematic Polar code based on decoding reliability is proposed. Considering different effects of channel noise on the decoding results of different code bits, the decoding reliability of each bit is calculated by using the Gaussian approximation method and sorted. The code bits with lower decoding reliability are chosen as the punctured positions to construct the punctured systematic Polar code. The influences of different puncturing methods on the bit error rate (BER) performance are analyzed. The BER performance of the systematic Polar code is compared with that of the non-systematic Polar code. The simulation results show that, with the same puncturing rate, the performance of the Polar code based on the puncturing method with decoding reliability is superior to that based on the random puncturing method. Meanwhile, compared with the non-systematic Polar code under the same condition, the systematic Polar code based on the puncturing method of decoding reliability exhibits better BER performance.
puncturing; decoding reliability; systematic Polar code; Gaussian approximation
第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.005
2016-07-26. 作者简介: 赵生妹(1968─), 女, 博士, 教授, 博士生导师, zhaosm@njupt.edu.cn.
国家自然科学基金资助项目(61271238, 61475075)、江苏省研究生培养创新工程资助项目(KYLX16_0663).
赵生妹,邵珠要,陈汉武.基于译码可靠性的系统Polar码删余方法[J].东南大学学报(自然科学版),2017,47(1):23-27.
10.3969/j.issn.1001-0505.2017.01.005.
TN911.2
A
1001-0505(2017)01-0023-05

