直觉模糊序信息系统的变精度与程度“逻辑差”粗糙集*

李志明，唐永中

河西学院 信息技术中心，甘肃 张掖 734000

直觉模糊序信息系统的变精度与程度“逻辑差”粗糙集*

李志明+，唐永中

河西学院 信息技术中心，甘肃 张掖 734000

将直觉模糊集合中元素的隶属度、非隶属度和犹豫度充分地结合起来，在直觉模糊信息系统中定义了二次加权得分函数。基于此得分函数定义了直觉模糊信息系统中的优势关系，进一步地，通过“逻辑差”的方式将变精度粗糙集和程度粗糙集结合起来，提出了变精度与程度“逻辑差”粗糙集模型，并研究了其相关性质，发现“逻辑差”组合能够同时考虑变精度和程度的双重量化信息。最后，通过实例分析，进一步体现了研究意义，为直觉模糊序信息系统的知识发现提供了理论基础。

变精度粗糙集；程度粗糙集；逻辑差；直觉模糊序信息系统

1 引言

粗糙集理论是由文献[1]提出的一种解决信息不完备、不精确系统的有效数学工具，广泛应用于数据挖掘、人工智能、决策分析和智能信息处理与知识获取等领域中[2-5]。经典的粗糙集是以完备信息系统为研究对象，以等价关系为基础的理论。然而在实际问题中很多信息系统是基于优势关系的[6-7]，经典的粗糙集理论已不适用于解决此类问题。

由于经典粗糙集的等价类与概念集之间的包含关系太过严格，没有考虑某种程度上的子集关系和知识等价类与概念集相交关系的相对量化信息，其在实际应用中具有一定的局限性。于是Ziarko在1993年通过引入误差参数提出了变精度粗糙集模型[8]，对属性之间没有函数关系的数据问题进行处理。Yao和Lin[9]在1996年通过研究粗糙集与模态逻辑间的关系构建了程度粗糙集模型。变精度粗糙集模型[10]与程度粗糙集模型[11-12]分别从相对量化和绝对量化的角度对近似空间进行描述，它们从两个不同的角度去刻画同一概念，两个指标既有其优势及适用环境，又是相辅相成的关系。因此，变精度与程度粗糙集模型的复合研究具有深远意义。

经典Pawlak粗糙集中的等价关系要求过于严苛，因此基于优势关系将变精度、程度粗糙集通过逻辑组合结合起来研究具有重要的理论价值。相关学者已经在序信息系统下对变精度相对量化信息和程度绝对量化信息的复合模型做了部分研究[13-14]。本文在此基础上，基于变精度与程度粗糙集的逻辑组合，构建了直觉模糊信息系统的变精度与程度“逻辑差”粗糙集模型，并对其粗糙区域和基本性质进行深入研究，以形成对近似空间变精度相对量化与程度绝对量化的复合描述。最后通过案例分析该理论的有效性和实用性。

2 预备知识

3 直觉模糊序信息系统下变精度与程度“逻辑差”粗糙集

上文对序信息系统、优势关系下变精度粗糙集、程度粗糙集的基本知识进行了简要介绍，下面基于直觉模糊序信息系统，研究变精度与程度“逻辑差”粗糙集的内容，并深入讨论该模型的重要性质。

首先，因为隶属度、非隶属度和犹豫度3个因素会同时对决策评价产生影响，而且减少单个因素对评价的影响可以使决策更加贴近实际，所以在直觉模糊信息系统中，定义了二次加权得分函数。此加权得分函数除了0和1两个极端值之外，在区间(0，1)能够减少单因素（线性加权[14]Sa(x)=ω1μa(x)-ω2νa(x)-ω3πa(x)）对加权得分函数的影响，其效果如图1所示。

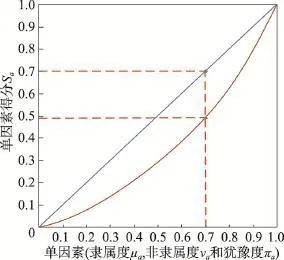
Fig.1 Comparison of linear weighted and square weighted图1 线性加权与二次加权的比较

4 算法设计

为了验证本文所提出的定义和定理的有效性和可行性，设计了相应的算法（算法1）来求解X的上近似集、下近似集和负域（因正域恒为空集，所以不用求解），并分析了算法的求解步骤与时间复杂度。

算法1计算直觉模糊序信息系统的上、下近似集和负域

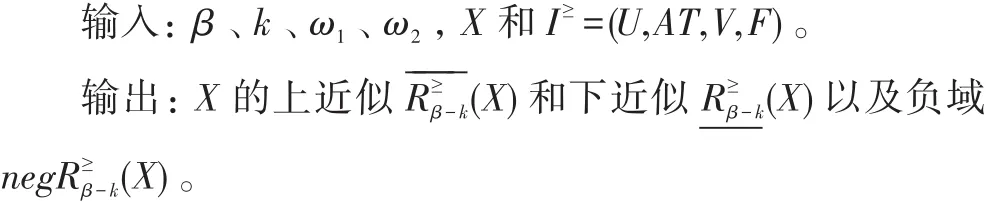
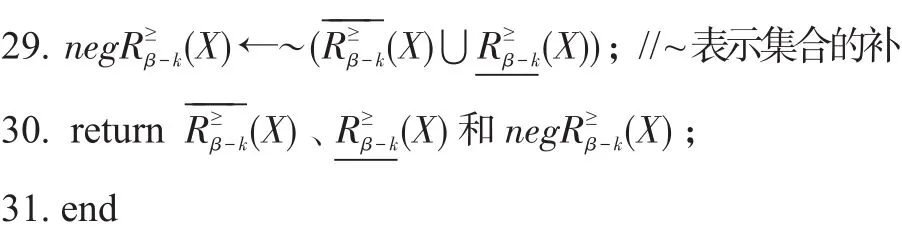
在算法1中，第2步将X的上、下近似集初始化为∅；第3步到第7步计算论域U上所有对象在属性集AT下的二次加权得分；第8步到第28步求解“逻辑差”上下近似，其中第10步到第21步求解x在属性集AT下的优势类，第22步到第24步求解X的上近似集，第25步到第27步求解X的下近似集；第29步计算X的负域；第30步返回X的上近似集和下近似集。第2步的时间复杂度为O(1)，第3步到第7步的时间复杂度为O(|U|×|AT|)，第8步到第28步的时间复杂度为O(|U|2×|AT|)，第29步的时间复杂度为O(U)，第30步的时间复杂度为O(1)，因此算法1的时间复杂度为O(|U|2×|AT|)。

5 案例研究

在装备采购中，存在多个装备供应商可供选择，对供应商的资格评价是供应商选择的关键问题。某型军用装备邀请招标，已经投标入围的有5家供应商，分别为a1、a2、a3、a4、a5，但合同仅授予其中的一家。特邀20名专家U={x1,x2,…,x20},对入围的5家供应商进行评判，现将专家当时的满意程度与不满意程度列在表1。表1中的直觉模糊数可通过专家是否满意的形式来获取，如专家x1对于属性a4的隶属度与非隶属度，可通过下面的方法来确定：邀请10位专家，对5名供应商进行投票，若有4个满意，5个不满意，1个弃权，即有1位专家在满意与不满意之间持犹豫意见。这时认为专家x1对属性a4的隶属度为0.4，非隶属度为0.5，而犹豫度为0.1，记作f(x1,a4)=〈0.4,0.5＞，其他的直觉模糊数可类似得到。

这里，隶属度权重ω1和非隶属度权重ω2分别表示满意程度和不满意程度的权重，ω1和ω2可根据不同的需求来设置。一般而言对于满意和不满意程度，人们往往更看中满意程度，对于不满意程度和犹豫度往往不太看重，因此本文设置ω1=0.6，ω2=0.2，那么犹豫度ω3=0.2。对于精度β和程度k往往会根据需求而自行选择，因此本文设置β=0.6，k=1。通过定义5计算得到二次加权得分如表2。

Table 1 Satisfaction and dissatisfaction of experts for suppliers表1 专家对供应商的满意程度与不满意的程度

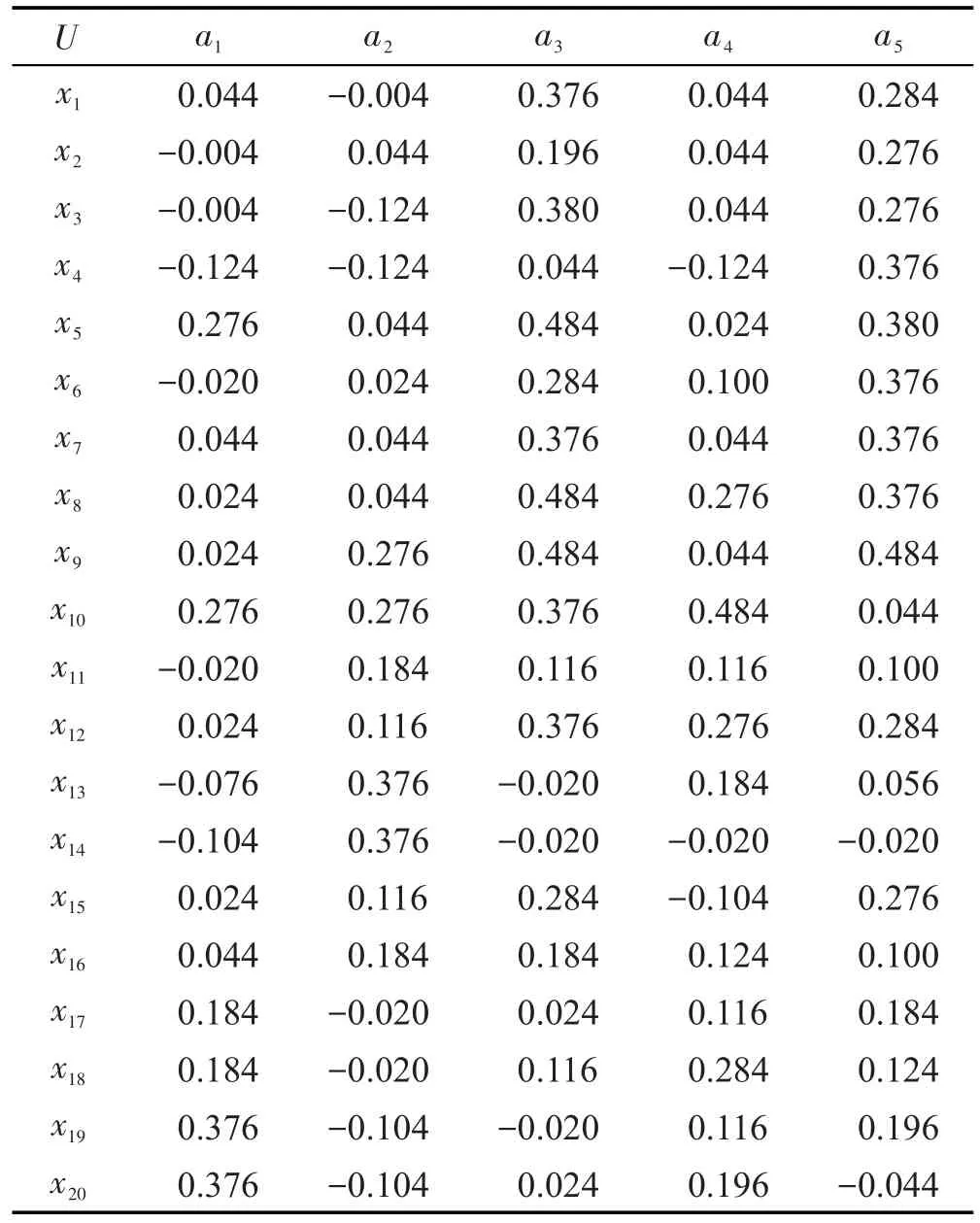
Table 2 Square weighted score表2 二次加权得分表

运用表2的二次加权得分和定义6可以计算论域U中所有对象的优势类，所有的优势类见表3。

随机抽取一部分对象集X={x2,x4,x5,x6,x11,x12,x15,x16,x17,x20}作为研究对象。X的上、下近似集分别为：

进而，X的正域和负域分别为：

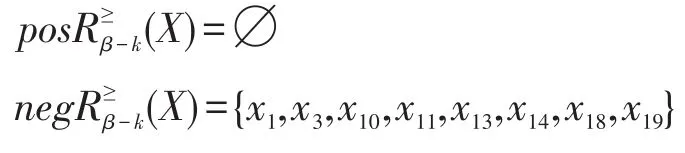
通过X的上、下近似集可以得到X的更为精确的描述，X的上近似集排除了对象x2、x4、x6、x11、x15，X的下近似集只剩下对象x2和x4。那么当进行决策时可以重点考虑x2和x4两位专家的意见，次要地考虑x5、x12、x16、x17、x20这5位专家的意见，可以不用考虑x6、x11、x15这3位专家的意见，从而可以减少因专家之间的不同意见而难以得出最终的决策。

Table 3 Dominance class of all objects inU表3 论域U中所有对象的优势类

6 结论

本文通过定义二次加权得分函数得到一种新的排序规则，在此规则下定义了直觉模糊序信息系统，并通过“逻辑差”的方式把该序信息系统下的变精度粗糙集与程度粗糙集结合起来，使信息系统的量化更加精确。最后，通过实例对本文提出的定义与定理进行分析。本文的相关工作为直觉模糊序信息系统中的知识发现奠定了理论基础。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.

[2]Pawlak Z.Rough set theory and its applications in data analysis[J].Cybernetics and Systems,1998,29(7):661-688.

[3]Greco S,Matarazzo B,Slowinski R.Rough sets theory for multi-criteria decision analysis[J].European Journal of Operational Rrsearch,2001,129(1):1-47.

[4]Pawlak Z,Skowron A.Rough sets:some extensions[J].Information Sciences,2007,177:28-40.

[5]Chen Jinkun,Li Jinjin.An application of rough sets to graph theory[J].Information Sciences,2012,201:114-127.

[6]Dembczyński K,Pindur R,Susmaga R.Domnance-based rough set classifier without induction of decision rules[J]. Electronic Notes Theory Computer Science,2003,82(4): 84-95.

[7]Dembczyński K,Pindur R,Susmaga R.Generation of exhaustive set of rules within dominance-based rough set approach[J].Electronic Notes Theory Computer Science,2003, 82(4):96-107.

[8]Ziarko W.Variable precision rough set model[J].Journal of Computer System Science,1993,46(1):39-59.

[9]Yao Y Y,Lin T Y.Generalization of rough sets using modal logics[J].Intelligent Automation and Soft Computing,1996, 2(2):103-120.

[10]Zhang Xianyong,Mo Zhiwen.Variable precision rough sets [J].Pattern Recognition and Aartificial Intelligence,2004, 17(2):151-155.

[11]Liu Caihui,Miao Duoqian,Zhang Nan.Graded rough set model based on two universes and its properties[J].Knowledge-Based Systems,2012,33(3):65-72.

[12]Zhang Xianyong,Mo Zhiwen,Xiong Fang,et al.Comparative study of variable precision rough set model and graded rough set model[J].International Journal of Approximate Reasoning,2012,53(1):104-116.

[13]Li Mengmeng,Xu Weihua.Rough fuzzy set of logical and operation of variable precision and grade based on dominance relation[J].Journal of Frontiers of Computer Science and Technology,2016，10(2):277-284.

[14]Hu Meng,Guo Yanting,Xu Weihua.The“logical or”rough set theory of variable precision and grade based on dominance relation in intuitionistic fuzzy information system[J]. Operations Research and Fuzziology,2016,6(2):66-77.

[15]Xu Weihua.Ordered information systems and rough sets theory[M].Beijing:Science Press,2013.

附中文参考文献：

[10]张贤勇,莫志文.变精度粗糙集[J].模式识别与人工智能，2004,17(2):151-155.

[13]李蒙蒙,徐伟华.优势关系下变精度与程度的“逻辑且”粗糙模糊集[J].计算机科学与探索,2016,10(2):277-284.

[14]胡猛,郭艳婷,徐伟华.优势关系下直觉模糊信息系统的变精度与程度“逻辑或”粗糙集[J].运筹与模糊学,2016,6 (2):66-77.

[15]徐伟华.序信息系统与粗糙集[M].北京:科学出版社,2013.

LI Zhiming was born in 1980.He received the M.S.degree from Northwest Normal University in 2014.Now he is a lecturer at Hexi University.His research interests include artificial intelligence,computer network management and machine learning.

李志明（1980—），男，甘肃民乐人，2014年于西北师范大学获得硕士学位，现为河西学院讲师，主要研究领域为人工智能，计算机网络管理，机器学习。

TANG Yongzhong was born in 1964.He is a professor at Hexi University.His research interests include computer network management and machine learning.

唐永中（1964—），男，甘肃民勤人，河西学院教授，主要研究领域为计算机网络管理，机器学习。

“Logical Difference”Rough Set Theory of Variable Precision and Grade in Intuitionistic Fuzzy Ordered Information System*

LI Zhiming+,TANG Yongzhong
Center for Information Technology,Hexi University,Zhangye,Gansu 734000,China
+Corresponding author:E-mail:lzm@hxu.edu.cn

This paper comprehensively combines the membership,non-membership and hesitancy degree of the elements of intuitionistic fuzzy set,and defines the square weighted score function in the intuitionistic fuzzy information system.Based on the score function,this paper constructs the dominance relation of intuitionistic fuzzy information system,furthermore,proposes the“logical difference”rough set model of variable precision and grade,and studies related properties of the model,which takes into account the“logic difference”combination of the variable precision and grade at the same time.Finally,the significance of the theory is embodied by a case of analysis,which provides a theoretical basis for the knowledge discovery of the intuitionistic fuzzy ordered information system.

variable precision rough set;graded rough set;logical difference;intuitionistic fuzzy ordered information system

10.3778/j.issn.1673-9418.1606036

A

TP18

*The Research Foundation forYoung Teachers of Hexi University under Grant No.QN2014-25(河西学院青年教师科研基金资助项目).

Received 2016-06,Accepted 2016-08.

CNKI网络优先出版:2016-08-15,http://www.cnki.net/kcms/detail/11.5602.TP.20160815.1659.014.html

LI Zhiming,TANG Yongzhong.“Logical difference”rough set theory of variable precision and grade in intuitionistic fuzzy ordered information system,Journal of Frontiers of Computer Science and Technology,2017, 11(2)：333-340.