高效求解方法的核典型相关分析算法*

林克正，王海燕，李 骜，荣友湖

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

高效求解方法的核典型相关分析算法*

林克正+，王海燕，李 骜，荣友湖

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

针对高维小样本数据在核化图嵌入过程中出现的复杂度问题，引入基于核化图嵌入（kernel extension of graph embedding）的快速求解模型，提出了一种新的KGE/CCA算法（KGE/CCA-St）。首先将样本数据投影到维数远低于原样本空间维数的总体散度矩阵对应的秩空间，然后采用核典型相关分析进行特征提取，整个过程减少了核矩阵的计算量。在Yale人脸库和JAFFE人脸库上进行仿真实验，结果表明这种KGE/CCA算法的识别率明显优于KFD、KLPP和KNPE算法的识别率；和传统的KGE/CCA算法相比，在不影响识别率的情况下，KGE/CCA-St算法有效减少了计算时间。

核化图；典型相关分析；降维处理；散度矩阵

1 引言

人脸识别过程主要包括人脸图像检测、特征提取、模式识别匹配等几个流程，其中特征提取环节是人脸识别整个流程中最核心的步骤[1]。线性特征提取方法，是对原始样本进行线性映射并变换到一个低维空间进行鉴别信息的提取，提取出来的是人脸图像的线性特征。目前，产生了大量经典的线性特征提取方法，在各个领域得到了广泛的应用，其中主要有主成分分析（principal component analysis，PCA）[2]、线性鉴别分析（linear discriminant analysis，LDA）[3]等方法。

典型相关分析（canonical correlation analysis，CCA）方法，也是一种线性特征提取方法，提取的是人脸数据的线性特征。该方法通过找到两组特征之间的相关性，并使其最大化[4]，去除了特征间的冗余信息，最后将两组特征融合成一个特征。CCA融合后的特征具有统计不相关性，同时增加了特征信息量，然而人脸图像数据中非线性的鉴别信息没有被充分地挖掘出来，而这些未被挖掘出来的非线性的鉴别信息往往是人脸识别分类的关键。核方法是一种有效的方法，用核方法来增强典型相关分析方法，不仅能剔除冗余信息，增强鉴别信息，还能解决人脸图像特征线性不可分问题，挖掘出非线性因素。经核方法扩展后的典型相关分析，表征能力更强[5]，更有助于人脸识别。近年来，还涌现出了核算法与一些经典线性算法相结合的算法[4]，如核主成分分析方法（kernel principal component analysis，KPCA）[6]、核线性鉴别分析（kernel linear discriminant analysis，KLDA）[7]、核Fisher判别（kernel Fisher discriminant analysis，KFD）[8]、核局部保持投影（kernel locality preserving projection，KLPP）[9]、核邻域保持嵌入（kernel neighborhood preserving embedding，KNPE）[10]等。这些基于核函数的方法都可以被归纳为核化图嵌入（kernel extension of graph embedding，KGE）[11]。

在核典型相关分析算法的研究中发现，在核的图嵌入过程中，核矩阵中的内积运算的时间复杂度由样本数量和样本矢量维数决定。针对核化图算法中核矩阵计算量大的问题，引入了一种基于核化图高效求解的方法，即在对样本进行核化图嵌入之前就先对样本进行降维处理，大大减少了计算量；然后对降维后的样本数据进行核映射处理；最后再找出投影到高维特征空间的投影矢量之间的典型相关关系。这样得出了一种高效求解方法的核典型相关分析算法，达到减少存储空间和计算时间的目的。这个处理过程为高效快速的人脸识别打好了基础[12]。

2 典型相关分析

典型相关分析研究的是两个随机矢量的相互关系[13]，将两组随机矢量之间的研究简化成几对变量特征的研究[14]，是一种非常有效的多元统计方法。此方法应用到人脸识别领域中的特征提取过程时，就是在线性空间下，建立两组特征向量之间的相关准则函数，求得投影矢量集，然后将两组特征矢量之间的典型相关性特征作为有效鉴别信息[15]，既达到了信息融合的目的，还消除了特征之间的冗余信息[16]。设有两个样本分别为，CCA方法的目标是对两个等式和进行组合求解，找出使这两个等式之间的相关性达到最大的两组基向量φx∈ℜp和φy∈ℜq。假设变量Cxx和Cyy分别表示样本X和Y的协方差矩阵，Cxy表示样本X和样本Y的互协方差矩阵，E[·]表示期望。因此CCA方法的目标函数可表示为：

式（1）中：

根据式（1）中定义的相关系数，CCA方法的准则函数可转化为求解式（2）：

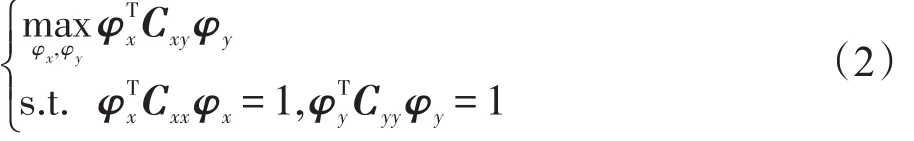
求投影轴φx和φy方向上的特征值，且求得的特征值满足。在所求得的特征值中选d对(d≤r)非零的特征值，求解出这d对特征值对应的特征向量，这些特征向量将被当作典型投影方向φxi和φyi，i=1,2,…,d，因此φxi和φyi可作为提取特征x∗和y∗。

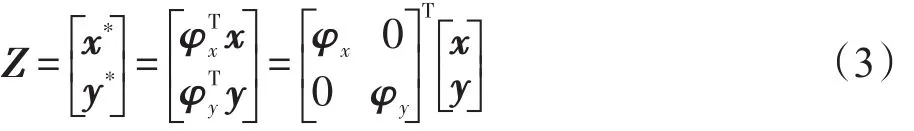
3 核化图嵌入算法

图嵌入的基本思想是找到原始训练样本的低维特征结构，同时保留高维特征空间顶点的相似性，也即找到符合这两个要求所对应的投影矢量a或者投影矩阵A（如果需要多个投影矢量）。对于一个原始训练样本数据X={x1,x2,…,xN}∈Rp×N，假设变量W为其相似度矩阵，图G={X,W}是一个无向有权图。原始样本中的每一个点xi表示这个图中的一个顶点，而矩阵中的每个度量表示样本间的相似度，衡量样本间近邻点的相似度。因此相似度矩阵中的矩阵度量值可表示如下：

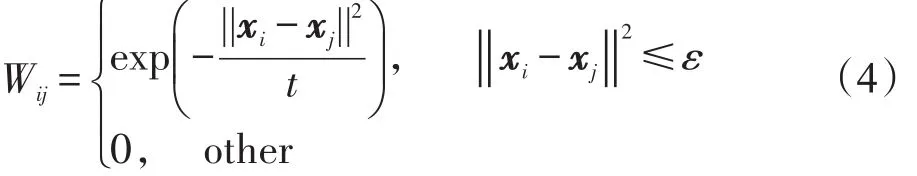
假设图G的拉普拉斯矩阵为L，则拉普拉斯矩阵的定义式可以用相似度矩W和一个对角矩阵D来定义，它的对角元素的值为W对应的一行元素值的和，如式（5）所示：

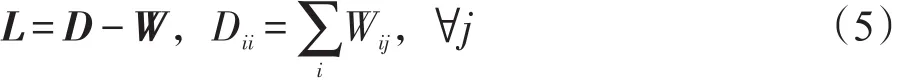
因此，图嵌入就是在保留高维空间中顶点相似性的同时，找到一个原始数据的低维表示，即X∗=ATX。由以上分析可以得到一个线性图嵌入框架的准则函数如式（6）：

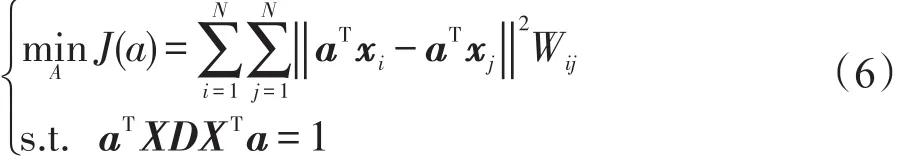
通过求解式（7），可得最优投影矢量a∗：

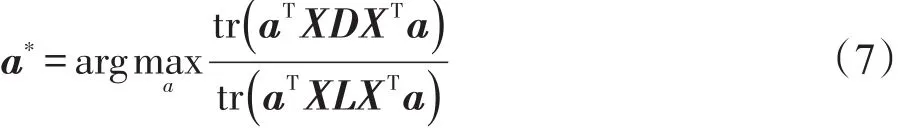
核化图嵌入则是在线性图嵌入框架的基础上，引入了非线性映射K，替换了线性内积，解决了原始样本中存在低维空间不可线性化问题[17]。设原始训练样本为X，则原始样本经过非线性映射K后，样本可表示为K(X)={K(x1),K(x2),…,K(xN)}。因此在原始训练样本通过非线性映射后，由于满足aTK(X)LK(X)Ta=1，核化图嵌入框架的最优投影可表示为：

a∗可通过求解下式的最大特征值所对应的特征向量得到：

4 高效求解方法的KGE/CCA算法

4.1 KGE/CCA算法的具体理论推导

假设原始训练样本中有两个样本分别为X={x1,x2,…,xN}∈Rp×N和Y={y1,y2,…,yN}∈Rq×N，这两个样本无向有权图可分别表示为G={X,Wx}，G={Y,Wy}，其中Wx和Wy分别为X和Y相似度矩阵，矩阵中的度量表示样本间的相似度，分别代表X和Y中的样本i和j的相似度，它们的定义可参考式（4）。

假设两个样本最后求得的最优投影为α∈Rp和β∈Rq，设分别为两个样本核化后在高维特征空间中测试样本的均值向量，则有表达式和表达式。核函数的均值化处理，使得小样本问题下高维特征空间中有效鉴别信息得到了较好的保留。根据式（8）可得两个样本的在高维特征空间的KGE方法的目标函数分别为式（10）和（11）：

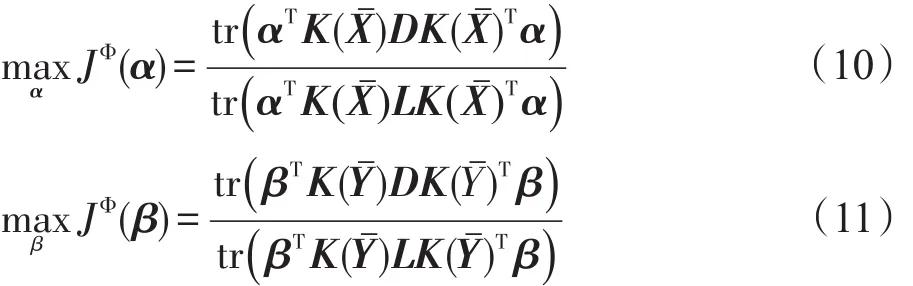
原始样本在高维特征空间的投影可通过式（10）和（11）来计算，这样便将原始样本投影到低维特征空间，提取了样本数据的非线性特征。为了保证提取的非线性特征具有统计不相关性，再采用CCA方法，找到核化图嵌入后的映射到高维特征空间中向量之间的相关关系，找到鉴别矢量，最终融合成一个特征。找到投影到高维特征空间中两个向量之间的典型相关性，即找到投影方向上和投影方向上的相关性最大。其中假设变量Cxx和Cyy分别表示样本X和Y的协方差矩阵，Cxy表示样本X和样本Y的互协方差矩阵，由典型相关分析方法的原理，可得KGE/ CCA方法的目标函数为式（12）：

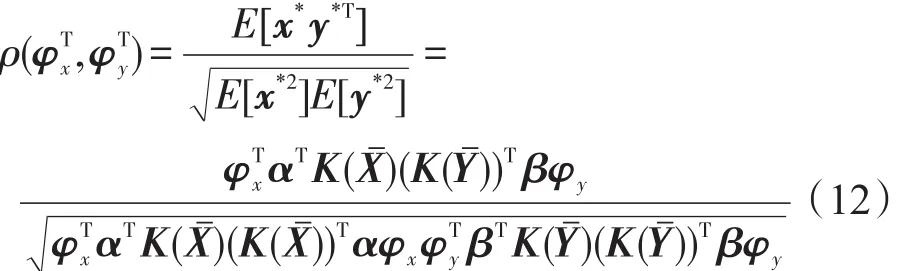
等价于式（13）：

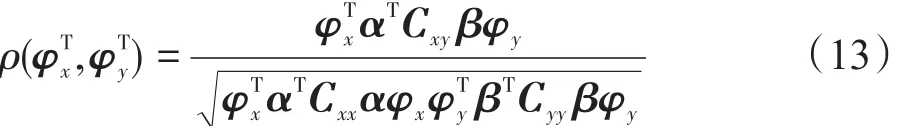
其中，Cxx、Cyy、Cxy分别定义如下：

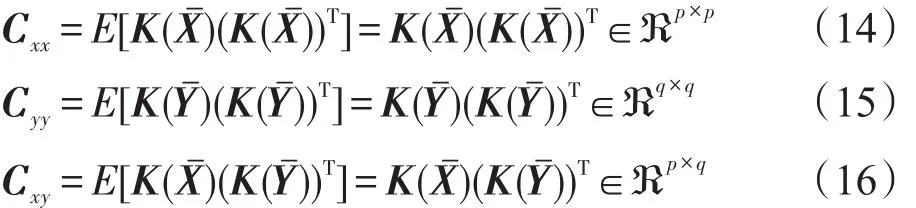
又由于

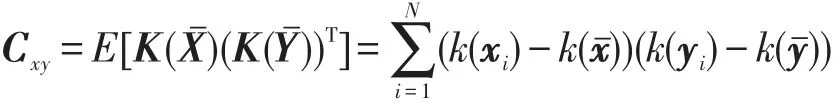
且存在以下两个等式：

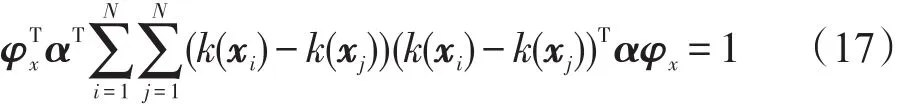
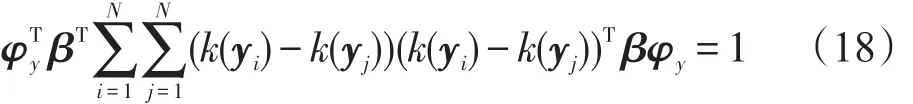
因此，KGE/CCA方法的准则函数为：

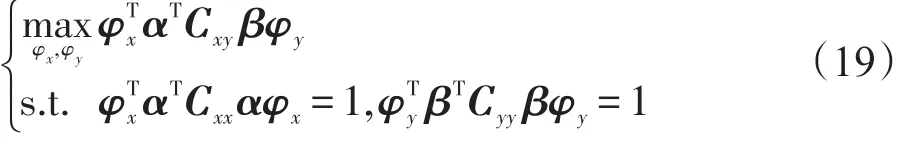
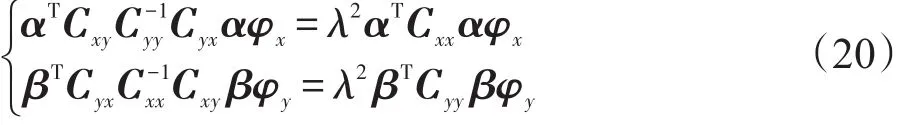
4.2 核化图嵌入算法的高效求解模型的引入

KGE/CCA方法融合了核化图嵌入算法和典型相关分析算法，对两个样本进行处理的过程中需要大量的计算。整个算法过程中，在核化图嵌入之前，先对样本进行降维处理。将一种减少计算量的同时不影响最终结果的求解模型引入进来，形成的新方法暂且记为KGE/CCA-St。先将样本降维到一个低维的特征空间，以减少维数。这个低维特征空间可以由总体散度矩阵St的非零特征值所对应的特征向量来求得。由于St的秩远远小于维数，故这种方法能够起到降维的目的。总体散度矩阵St由下式计算：

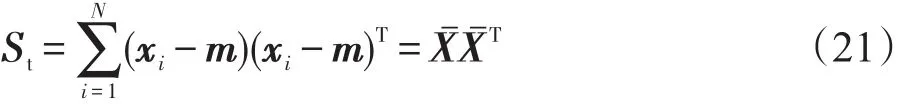
对原始样本采用PCA算法降维，投影到总体散度矩阵St的非零特征值对应的特征空间，记为H。在这个秩空间H中存在一个子空间Φt=span{α1,α2,…,αm}，并且设在这个H空间中St为总体散度矩阵，为H空间中子空间Φt的正交补空间。由此可知，这个正交补空间为协方差矩阵的零空间，则式（22）成立：

由上式可知，假设ϕ∈Φt，δ∈，φ∈H，则φ=ϕ+δ成立，由于为协方差矩阵的零空间，则式（23）成立：

以西门子MM420变频器为例，为使S7-200 PLC与MM420变频器以USS协议通讯，需要对MM420变频器做的参数设置如下[8]：

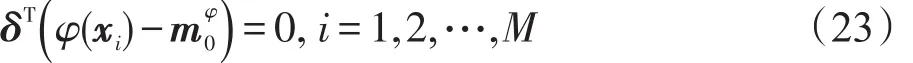
也就是等式Jφ(φ)=Jφ(ϕ)成立，因此对于核化图嵌入算法的目标函数式（8）中为了不损失任何有效的鉴别信息，可以从ϕ中选取鉴别矢量。将原始样本转换到总体散度矩阵对应的秩空间，之后进行核化图操作，不影响鉴别信息的提取。因此，此种模型可以作为核典型相关分析的一种节省时间的快速求解方法。

4.3 KGE/CCA-St算法描述

根据KGE/CCA-St算法理论的具体推导过程，可以得到KGE/CCA-St算法的结构图如图1所示。

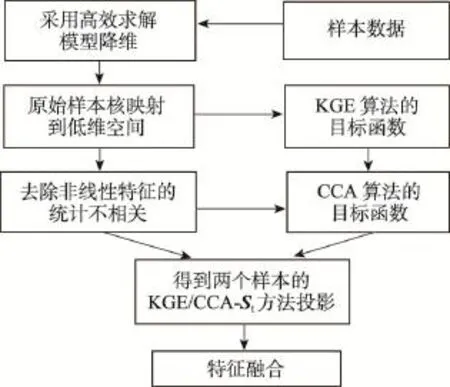
Fig.1 Steps of KGE/CCA-St图1 KGE/CCA-St算法步骤图

人脸图像的正确分类识别需要完成三部分的工作：采集人脸图像数据、特征提取和人脸识别。本文提出的快速求解方法的核典型相关分析算法（KGE/ CCA-St）的人脸识别流程如下：

5 实验结果与分析

选择在Yale和JAFFE标准的人脸库上进行仿真实验，采用高斯核函数k(x,y)=exp(||x-y||2σ)，σ= 5.5E+7。

（1）对基于核方法的4种降维算法，如KFD、KLPP、KNPE算法，与KGE/CCA算法进行比较实验，验证KGE/CCA算法的有效性。

（2）验证KGE/CCA算法和KGE/CCA-St算法的识别率的等效性。

首先在Yale标准人脸库上，在每个人脸类别里选择4幅图像作为实验的训练样本集，将其他的作为测试样本集。而在JAFFE人脸表情库上，每个人脸类别随机抽取5幅图像作为训练样本集，其他剩余的人脸图像将作为测试样本集。通过这两个人脸库的实验，考查KFD、KLPP、KNPE、KGE/CCA这4种算法的识别率随着特征维数的变化情况，结果如图2所示。

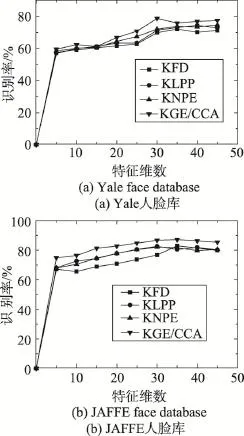
Fig.2 Comparison of recognition rate of 4 algorithms on different feature dimensions图2 不同特征维数下4种算法的识别率比较

由图2可知，在Yale人脸库中训练样本数为4时，本文KGE/CCA算法在特征维数为30时，识别率达到最高的78.7%，且算法的最高识别率相对其他3种算法的识别率都有较明显提高。在特征维数为20时，4种算法的识别率基本差不多，特征维数大于20之后，KGE/CCA算法表现出了优越性。在JAFFE人脸库的实验中，KGE/CCA算法在特征维数为35时，识别率达到最高的87.1%。本次实验结果图（b）较实验结果图（a）中的点相对稀疏，也就是说算法间的识别率差别较明显。这是由于JAFFE人脸库是一个表情变化较大的表情库，充分验证了本文提出的KGE/ CCA算法对于表情复杂的情况识别率较理想。KLPP、KNPE两种算法的图线波动变化不大，总体识别率较接近，而KGE/CCA较其他3种算法都有很明显的优势。

5.2 识别率与训练样本数的关系

分别在Yale和JAFFE标准的人脸库上做实验，考查4种识别算法在选择不同的训练样本个数i(i=2, 3,4)时，识别精度的变化范围。对实验所选的训练样本数组都重复实验10次，4种算法的识别率随不同训练样本数变化的情况如表1和表2所示。

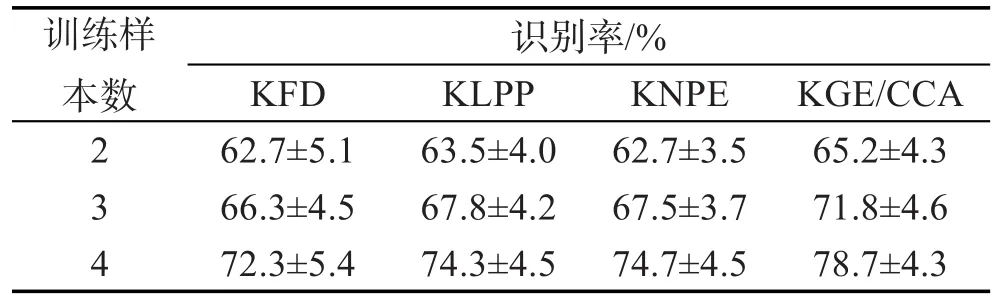
Table 1 Recognition rate comparison on Yale face database with different methods表1 在Yale人脸库中不同算法的识别率对比

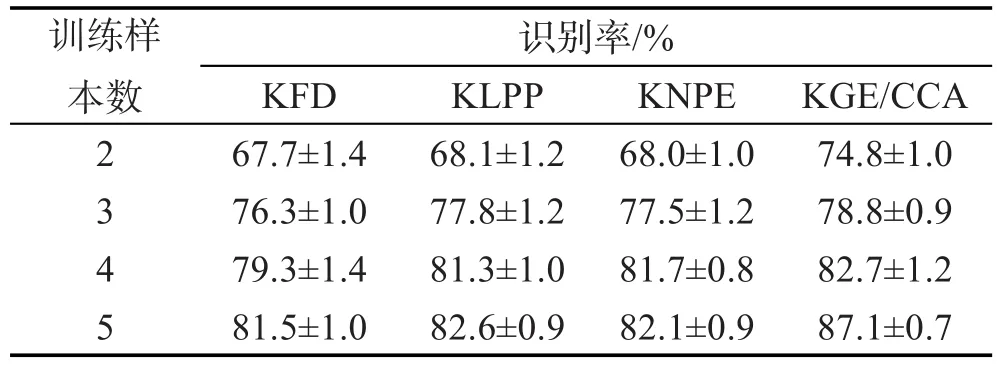
Table 2 Recognition rate comparison on JAFFE face database with different methods表2 在JAFFE人脸库中不同算法的识别率对比

由表1可知，在取样本数为2、3、4时，各算法间识别率差别不大，但是由识别率后面的数字可知，各算法在重复进行实验时，识别率波动范围较大。在不同的训练样本数下，KGE/CCA算法都较其他3种算法有明显的优越性。

由表2可得，4种算法在训练样本数较低的情况下的识别性能与较高时的识别性能差别较大，在取不同的训练样本数重复进行实验时，由识别率后面的数字可知，较上次实验中，波动范围较小，也就是算法的稳定性较高。无论训练样本个数选择多少，KGE/CCA算法的识别性能都明显高于其他3种算法。

5.3 KGE/CCA-St和KGE/CCA识别时间和识别率的比较

由于本文在核化图嵌入之前进行了降维处理，对于KGE/CCA算法整体引进了一种核化图嵌入算法的高效求解方法，引入求解模型的算法记为KGE/ CCA-St。对KGE/CCA-St和KGE/CCA算法的计算时间做了对比。首先在Yale标准人脸库上对每个不同的类别随机分别选择4幅图像作为实验的训练样本集，将其他的作为测试样本集。而在JAFFE人脸表情库上每个人脸类别随机抽取7幅图像作为训练样本集，其他剩余的人脸图像作为测试样本集。每次实验独立重复10次。表3为KGE/CCA-St和KGE/ CCA算法不同样本下计算时间的比较。

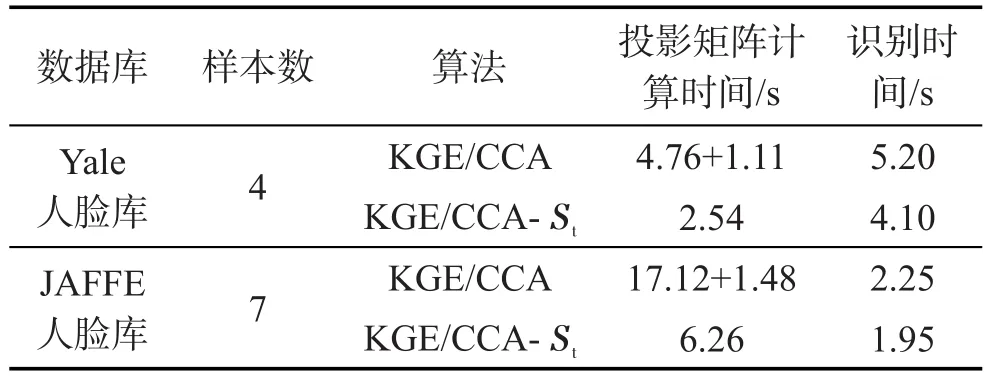
Table 3 Comparison of computing time between KGE/CCA-Stand KGE/CCA表3 KGE/CCA-St和KGE/CCA计算时间的比较

由表3的结果可以看出，本文KGE/CCA-St算法有效减少了计算时间，提升了计算速度，随着样本数的增加，计算过程所减少的时间占比也呈增加趋势。本实验中，样本数为4时，已经比KGE/CCA算法的时间减少了将近1/2，而样本数为7时，时间减少了将近2/3。

6 结束语

本文综合考虑核化图算法与典型相关分析算法的优点，结合核化图的一种高效求解方法，提出了一种基于核化图高效求解方法的核典型相关分析算法。一方面解决了人脸图像数据因光照、姿态、表情等原因引起的线性不可分的问题，找出了样本数据之间的相关关系，去除了冗余信息，同时在考虑样本零空间的基础上，充分挖掘了非零空间的鉴别信息；另一方面，核化图嵌入算法高效求解方法的引入，解决了计算量大和存储空间大的问题。实验结果证明了KGE/CCA-St算法具有较好的识别率和较低的运行时间。然而，本文在识别分类阶段，采用的是最简单的最近邻分类器，分类规则过于简单，在进一步的研究中，可以考虑其他分类器，或者加一些限制分类规则，从而取得更高的识别率。

[1]Wang Mingjun.Study of face recognition algorithm based on compressive sensing[D].Xi'an:Xidian University,2012.

[2]Worley B,Halouska S,Powers R.Utilities for quantifying separation in PCA/PLS-DA scores plots[J].Analytical Biochemistry,2013,433(2):102-104.

[3]Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[4]Hou Shudong,Sun Quansen.Sparsity preserving canonical correlation analysis with application in feature fusion[J]. ActaAutomatica Sinica,2012,38(4):659-665.

[5]Liu Fumin,Zhang Zhibin,Shen Jiquan.Emotion recognition based on multi-features fused by kernel canonical correlation analysis[J].Computer Engineering and Applications,2014,50(9):193-196.

[6]Zhao Jianhua,Wang Shunfang,Zhang Feilong.Face recognition study with combination-kernel-based KPCA[J].Computer Engineering and Design,2014,35(2):631-635.

[7]Lu Guifu,Lin Zhong,Jin Zhong.Uncorrelated kernel extension of graph embedding[J].Journal of Image and Graphics, 2011,16(4):618-624.

[8]Mika S,Ratsch G,Weston J,et al.Fisher discriminant analysis with kernels[C]//Proceedings of the 1999 IEEE Signal Processing Society Workshop,Neural Networks for Signal Processing IX,Aug 25,1999.Piscataway,USA:IEEE,1999: 41-48.

[9]Feng Guiyu,Hu Dewen,Zhang D,et al.An alternative formulation of kernel LPP with application to image recognition[J].Neurocomputing,2006,69(13):1733-1738.

[10]Lin Yu'e,Li Jingzhao,Liang Xingzhu,et al.Fast model for extension of graph embedding[J].Application Research of Computers,2012,29(12):4758-4760.

[11]Han P Y,Jin A T B,Kar A T.Kernel discriminant embedding in face recognition[J].Journal of Visual Communication and Image Representation,2011,22(7):634-642.

[12]Hu Haifeng,Zhang Ping,Ma Zhengming.Direct kernel neighborhood discriminant analysis for face recognition[J]. Pattern Recognition Letters,2009,30(10):902-907．

[13]Zhang Jianming,Yang Lirui,Wang Liangmin.Facial expression recognition based on hybrid features fused by CCA[J]. ComputerApplications,2008,28(3):643-647.

[14]Zhao Song,Zhang Zhijian,Zhang Peiren.Enhanced CCAand its applications in feature fusion of face recognition[J]. Journal of Ccomputer-Aided Design&Computer Graphics, 2009,21(3):394-399.

[15]Sun Quansen,Zeng Shenggen,Yang Maolong,et al.Combined feature extraction based on canonical correlation analysis and face recognition[J].Journal of Computer Research and Development,2005,42(4):614-621.

[16]Cheng Weiyue,Lin Kezheng,Liu Shuai,et al.Locally maintaining projection of typical correlation analysis[J].Joural of Harbin University of Science and Technology,2013,18 (5):65-69.

[17]Lu Guifu,Lin Zhong,Jin Zhong.Optimal discriminant analysis based on kernel extension of graph embedding and face recognition[J].Journal of Software,2011,22(7):1561-1570.

附中文参考文献：

[1]王明军.基于压缩感知人脸识别算法研究[D].西安:西安电子科技大学,2012.

[4]侯书东,孙权森.稀疏保持典型相关分析及在特征融合中的应用[J].自动化学报,2012,38(4):659-665.

[5]刘付民,张治斌,沈记全.核典型相关分析算法的多特征融合情感识别[J].计算机工程与应用,2014,50(9):193-197.

[6]赵剑华,王顺芳,张飞龙.基于组合核函数KPCA的人脸识别研究[J].计算机工程与设计,2014,35(2):631-635.

[7]卢桂馥,林忠,金忠.具有统计不相关性的核化图嵌入算法[J].中国图象图形学报,2011,16(4):618-624.

[10]林玉娥,李敬兆,梁兴柱,等.一种核化图嵌入算法的快速求解模型[J].计算机应用研究,2012,29(12):4758-4760.

[13]张建明,杨丽瑞,王良民.基于典型相关分析特征融合的人脸表情识别方法[J].计算机应用,2008,28(3):643-647.

[14]赵松,张志坚,张培仁.增强的典型相关分析及其在人脸识别特征融合中的应用[J].计算机辅助设计与图形学学报,2009,21(3):394-399.

[15]孙权森,曾生根,杨茂龙,等.基于典型相关分析的组合特征抽取及脸像鉴别[J].计算机研究与发展,2005,42(4): 614-621.

[16]程卫月,林克正,刘帅,等.典型相关分析的局部保持投影算法[J].哈尔滨理工大学学报,2013,18(5):65-69.

[17]卢桂馥,林忠,金忠.基于核化图的最佳鉴别分析与人脸识别[J].软件学报,2011,22(7):1561-1570.

LIN Kezheng was born in 1962.He received the Ph.D.degree in control theory and control engineering from Harbin Engineering University in 2001.Now he is a professor and M.S.supervisor at Harbin University of Science and Technology.His research interests include image processing,machine vision and pattern recognition,etc.

林克正（1962—），男，山东蓬莱人，2001年于哈尔滨工程大学控制理论与控制工程专业获得博士学位，现为哈尔滨理工大学教授、硕士生导师，主要研究领域为图像处理，机器视觉，模式识别等。发表学术论文70余篇，主持完成了黑龙江省教育厅科研基金项目，承担过国家科技攻关项目。

WANG Haiyan was born in 1988.She is an M.S.candidate at Harbin University of Science and Technology.Her research interests include image processing and pattern recognition,etc.

王海燕（1988—），女，黑龙江齐齐哈尔人，哈尔滨理工大学计算机科学与技术专业硕士研究生，主要研究领域为图像处理，模式识别等。

LI Ao was born in 1986.He received the Ph.D.degree in communication and information systems from Harbin Engineering University in 2014.Now he is a lecturer at Harbin University of Science and Technology.His research interests include sparse representation,image restoration and computer vision,etc.

李骜（1986—），男，黑龙江哈尔滨人，2014年于哈尔滨工程大学通信与信息系统专业获得博士学位，现为哈尔滨理工大学讲师，主要研究领域为稀疏表示，图像复原，计算机视觉等。主持国家自然科学基金1项、黑龙江省自然科学基金1项，参与船舶工业国防科技预研项目1项，发表学术论文10余篇，授权发明专利1项。

RONG Youhu was born in 1989.He is an M.S.candidate at Harbin University of Science and Technology.His research interests include image processing and pattern recognition,etc.

荣友湖（1989—），男，江西萍乡人，哈尔滨理工大学计算机应用技术专业硕士研究生，主要研究领域为图像处理，模式识别等。

Kernel Canonical CorrelationAnalysis Based on Solving Method with High Efficiency*

LIN Kezheng+,WANG Haiyan,LIAo,RONG Youhu
School of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China
+Corresponding author:E-mail:link@hrbust.edu.cn

Aiming at the problem of the complexity of high dimensional small sample data during the process of KGE (kernel extension of graph embedding),by a fast calculation model based on KGE,this paper proposes a new KGE/ CCA algorithm(KGE/CCA-St)which can reduce the computational complexity of kernel matrix.Firstly,sample data are projected into corresponding rank space of total scatter matrix in which the dimension is far lower than that in original sample space.Then,kernel canonical correlation analysis is used for feature extraction,the calculation of kernel matrix is decreased in this process.Through the simulation experiments on Yale face database and JAFFE face database,the results show that the recognition rate of the KGE/CCA algorithms is significantly better than that of KFD, KLPP and KNPE algorithms.Compared with the traditional KGE/CCA algorithm,KGE/CCA-Stcan effectively reduce the computation time without affecting the recognition rate.

kernel extension of graph;canonical correlation analysis;dimension reducing processing;scatter matrix

10.3778/j.issn.1673-9418.1512064

A

TP391.4

*The National Natural Science Foundation of China under Grant No.61501147(国家自然科学基金);the Natural Science Foundation of Heilongjiang Province under Grant No.F2015040(黑龙江省自然科学基金).

Received 2015-12,Accepted 2016-04.

CNKI网络优先出版:2016-04-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160408.1642.004.html

LIN Kezheng,WANG Haiyan,LI Ao,et al.Kernel canonical correlation analysis based on solving method with high efficiency.Journal of Frontiers of Computer Science and Technology,2017,11(2)：286-293.