基于特征值多阈值修正的声矢量圆阵信源数检测
时胜国,祝文昭,李赢,朱中锐
(1.哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;2.哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)
基于特征值多阈值修正的声矢量圆阵信源数检测
时胜国1,2,祝文昭2,李赢2,朱中锐1,2
(1.哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;2.哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)
为了解决水下远程目标被动探测问题,提出了一种声矢量圆阵的信源数检测方法。该方法构造了声矢量圆阵声压与振速联合处理的协方差矩阵,并借鉴图像处理中双阈值检测概念,对协方差矩阵的特征值进行多阈值修正处理,利用信息论检测准则实现了声矢量圆阵的信源数检测。理论分析和仿真实验结果表明,本文算法可以有效地提高信息论检测准则的检测性能。水池试验结果也表明本文算法具有更好的噪声抑制能力以及更好的目标检测性能,进一步验证了算法的有效性。
声矢量圆阵;目标检测;声压振速联合处理;多阈值;特征值修正
声矢量传感器可空间共点同步的拾取声场中某点处的声压和质点振速的三个正交分量,较声压传感器可获取更多的声场信息。文献[1-2]将声矢量传感器的振速分量作为独立阵元的信息来处理,指出矢量阵列信号处理与声压阵列信号处理可由Kronecher积联系起来,然而这些算法并没有充分利用声矢量阵中声压和振速相干性。惠俊英等[3]提出基于平均声能流概念的声压振速联合处理具有良好的抗各向同性噪声的能力;文献[4]理论分析结果也进一步证实了各向同性噪声场中声压和振速是互不相关的。在上述信号处理思想基础上,白兴宇等[5-6]提出了一种基于声压振速联合处理的声矢量阵信源数检测与方位估计方法,将子空间方法的高分辨能力与声矢量阵的抗噪能力有机结合起来,实现了远程目标的检测与方位估计。
与声矢量线阵丰硕的研究成果相比,声矢量圆阵相关的研究报道较少,而关于目标检测方面研究成果则未见报道。圆阵具有360°无模糊的目标检测和方位估计性能,具有很大的优越性,因此在声呐和雷达系统中有着比较广泛的应用。贡彦飞等[7]在圆阵条件下通过GDE(gerschgorin disk estimator)方法实现了信源检测。张杰等[8]提出了基于对角加载技术的信源检测方法,通过实验验证了基于圆阵的该方法有效性。杨德森等[9]则提出了一种基于声压振速联合处理的声矢量圆阵相位模态域MUSIC估计算法,将声压振速联合处理的抗噪能力与圆阵的全方位估计性能相结合,实现了远程高分辨的目标定位。
本文提出了一种基于声压振速联合处理的声矢量圆阵目标信源数检测方法。首先构造了声矢量圆阵的声压振速联合处理的协方差矩阵借鉴图像处理中双阈值检测概念,对协方差矩阵的特征值进行多阈值修正处理,然后利用信息论检测准则实现对目标信源数的检测。
1 声矢量圆阵信号处理基础
1.1 声矢量圆阵接收信号模型
假设M元声矢量圆阵位于xOy平面内,半径为r,以x方向作为圆阵的0°方向。声矢量传感器振速分量x、y通道正轴方向分别沿着圆阵的径向、切向方向布放,如图1所示。针对浅海远程目标探测,本文不考虑振速垂直分量,只考虑振速水平分量。假设有K个不相关的远场窄带声源信号入射到声矢量圆阵上,则声矢量圆阵接收信号可写为如下形式:
(1)
式中:P(t)、Vr(t)、Vφ(t)分别为接收的声压信号、径向振速信号和切向振速信号,Ap(θ)、Avr(θ)、Avφ(θ)分别为声矢量圆阵的声压通道、径向振速通道、切向振速通道的阵列流型,S(t)为入射信号,Np(t)、Nvr(t)、Nvφ(t)分别为声矢量圆阵声压通道、径向振速通道、切向振速通道接收噪声。它们可以表示为
式中:
式中:apm表示第m个声矢量传感器接收的声压信号的导向矢量,avrm、avφm分别表示第m个声矢量传感器振速径向、切向分量对应的导向矢量,θi表示第i个声源信号的入射角度(i=1,2,…,K),λ表示信号波长。
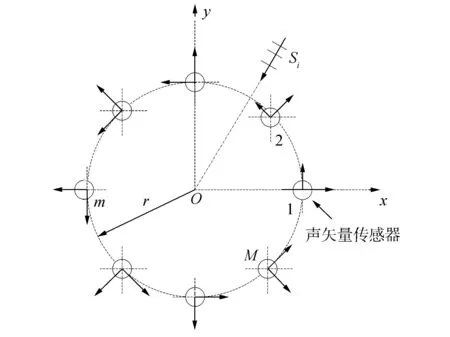
图1 声矢量圆阵示意图Fig.1 Schematic diagram of the uniform circular acoustic vector sensor array
1.2 基于声压振速联合处理协方差矩阵构造
将声矢量圆阵阵元振速切向和径向分量接收数据投影到笛卡尔坐标系xOy平面内x、y轴方向上,则第m个阵元接收振速信号变为
(2)
接收到的背景噪声变为
(3)
由理论可推得,投影变换并未改变声矢量圆阵接收的噪声场相关性和信号场的特征[9]。经过投影变换后,声矢量圆阵接收数据变换为
(4)
式中:P(t)表示声压信号,Vx(t)、Vy(t)分别表示投影后的振速x通道信号和振速y通道信号,Nx(t)、Ny(t)分别表示变换后的振速x、y通道的噪声信号,θi表示第i个入射信号的入射角度,且
通过电子旋转可得到组合振速Vc(t)、Vs(t):
(5)
式中:φ为指定观测方向,可采用Givens变换确定。
根据平均声能流概念,可得互协方差矩阵:
(6)
展开可得
(7)
式中:
(8)
对于各向同性噪声场,空间共点同步接收的声压振速信号是不相关的。假设声矢量圆阵不同阵元上接收的声压振速信号也是不相关的,则可得
(9)
所以
(10)
将式(10)代入式(7)得
(11)
其中
(12)
2 特征值的多阈值修正
2.1 声压振速互协方差矩阵特征值分析
假设存在K个不相关或不完全相干信号,由(11)式可知,理论上有
(13)
式中:λi和ui为第i个特征值及对应的向量。
将M个特征值由大到小排列:
(14)
但由于采样快拍有限及非均匀噪声等因素的影响,实际噪声特征值关系有
(15)
实际上,基于特征值的信源数检测准则(如AIC、MDL)是依据噪声特征值相似度进行信源数估计,式(14)会导致基于特征值的检测方法性能下降甚至失效。尽管由于上述限制导致噪声特征值发散,但M个特征值仍满足大特征值对应信号子空间、小特征值对应噪声子空间的关系。即在一定的信噪比条件下,信号特征值与噪声特征值之间的差值较大,而噪声特征值之间的差值较小。
2.2 信号与噪声子空间特征值的重划分
在理想条件下,且在信噪比较高时,噪声特征值之差较小,而信号特征值与噪声特征值的差异较大,特征值之差满足如下条件[10]:
(16)
根据文献[10]中参数设置,可设置一固定检测门限Lt1实现信号特征值与噪声特征值区分。在此基础上,借鉴图像处理中双阈值检测思想[11],再设置多个较小的检测门限,可实现对协方差矩阵的特征值进行多阈值修正处理。
具体步骤如下:
1)设置大小不同的两个阈值Lt1、Lt2,对特征值集合Cλ进行划分,得到信号特征值集合Cs1(λi≥Lt1)、争议区域CDis(Lt1>λi≥Lt2)以及噪声特征值集合Cn2(Lt2>λi);
2)定义待修正特征值集合CRev=CDis∪Cn2。
3)将CRev中特征值由小到大排列;设置一个新阈值Lti。
①若阈值Lti>Lt2,则可通过阈值Lti对待修正特征值集合CRev的特征值进行重新划分,形成两个特征值集合Csi和Cni,则可得特征值集合Cλ经过多阈值修正后的信号和噪声对应特征值集合Cs=Cs1∪Csi、CRev=Cni;
②若阈值Lti≤Lt2,则修正结束。
4)若阈值Lti>Lt2,重复步骤3)进行多次划分,形成信号对应特征值集合Cs与噪声对应特征值集合Cn=CRev。
为了实现特征值修正,还需对噪声对应的特征值集合Cn进行平均化修正处理,得到噪声对应修正后特征值λn。

(17)
其中:fix表示向下取整,Add表示加载值。
7)采用信息论检测准则[12-13]MDL方法实现信源数检测。
3 仿真实验及性能分析
在声压振速联合处理基础上,通过多阈值修正方法划分信号与噪声特征值,可提高噪声特征值的相似度,从而提高信息论检测准则的检测性能。下面对基于特征值多阈值修正的信息论检测准则信源数检测性能进行对比分析,仿真实验选取MDL信息论检测准则方法。本文方法阈值划分如下式:
(18)
3.1 声压和质点振速独立处理及声压振速联合处理对比分析
假设声矢量均匀圆阵元数为12元,阵半径r=0.7λ,信源入射方向60°,快拍数1 000,指定观测方向60°。仿真计算结果如图2所示,声压振速联合处理抗噪性能优于声压及质点振速处理方法。

图2 声压和质点振速独立处理及其联合处理方法对检测性能的影响Fig.2 The detection performance of acoustic pressure process, the independent process of acoustic pressure and particle velocity, and combined processing of acoustic pressure and particle velocity
3.2 不同检测方法仿真性能分析
假设声矢量均匀圆阵阵元数为12元,阵半径r=0.7λ,信源入射方向60°,快拍数1k,指定观测方向为60°。盖式圆检测准则GDE[14]的检测因子D(L)取值为1。仿真计算结果如图3所示,本文方法低信噪比下检测性能优于其他方法。
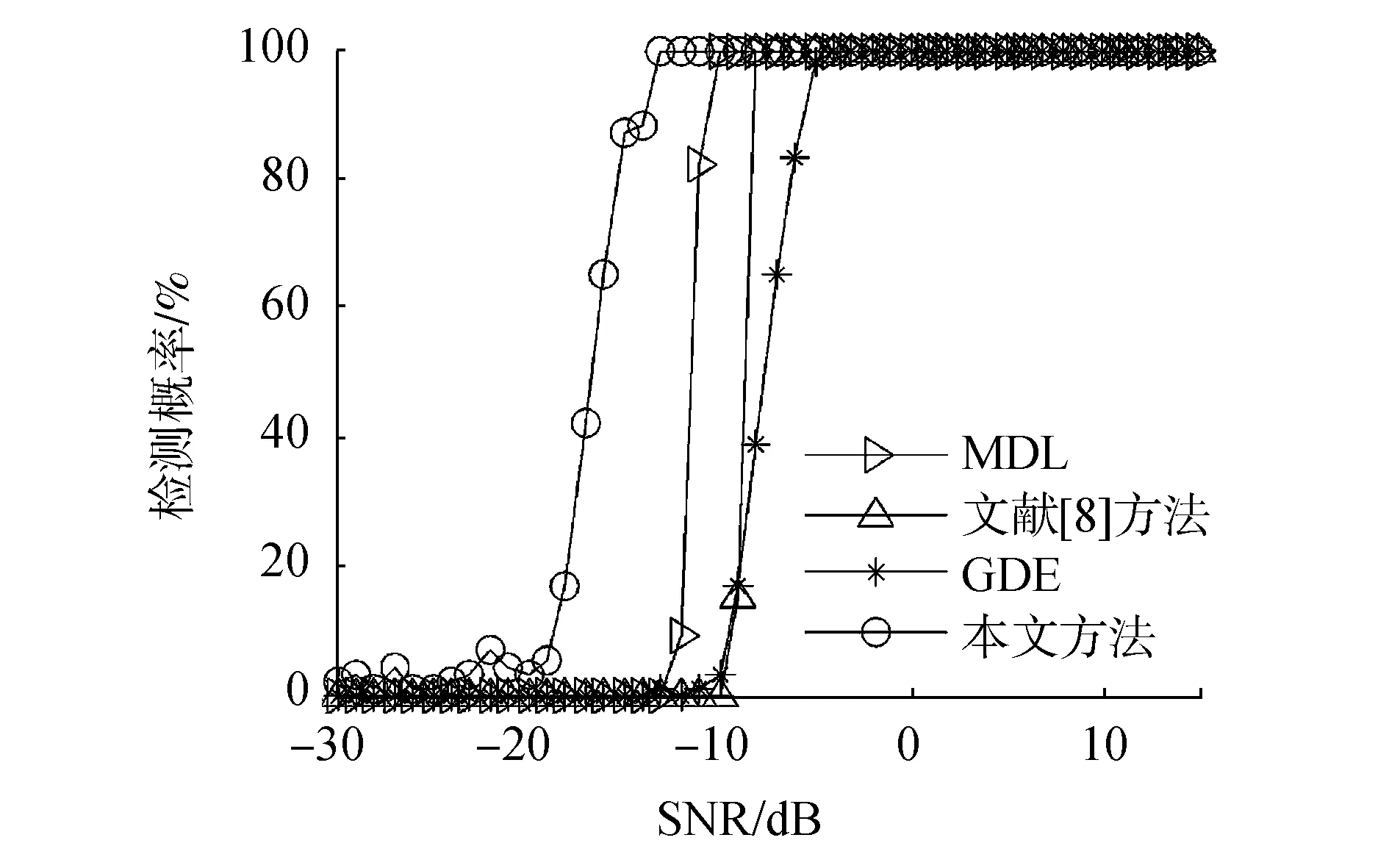
图3 不同检测方法的检测性能分析Fig.3 Analysis the detection performance of different methods
3.3 快拍数对检测性能的影响
假设声矢量均匀圆阵阵元数为12元,阵半径r=0.7λ,双信源入射方向分别为20°、35°,信噪比-10 dB,采用Givens变换确定指定观测方向。快拍数由100增至10 000。仿真计算结果如图4所示,MDL方法小快拍数条件下性能最佳,对比文献[8]方法及GDE方法,本文方法在小快拍数的条件下也具有较好的检测性能。

图4 快拍数对检测性能的影响Fig.4 Detection performance vs different number of snapshots
4 水池实验结果分析
为了进一步验证本文算法的可行性,开展了远程目标检测水池实验测试。实验阵列为8元声矢量圆阵,阵半径为0.35 m,如图5所示。每个声矢量传感器x和y正方向分别与该处的径向、切向重合。
实验中目标声源发射单频信号,声源距声矢量圆阵约16 m,位于6号声矢量传感器vx方向。滤波器通带频率500~5 000 Hz。定义信噪比SNR为
(19)
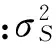
数据处理快拍数为1 000,指定观测方向为220°。声压、质点振速独立及其联合处理方法的检测结果如图6所示。质点振速独立处理方法的实质是将矢量传感器振速通道作为独立阵元处理,当背景噪声中存在非均匀噪声时,质点振速独立处理方法扩大了非均匀噪声的影响,使算法性能下降。并且由于实际的阵元布放并不能满足理想条件,声压振速联合处理方法性能下降,但仍优于其他两种方法。

图5 8元声矢量圆阵Fig.5 Uniform circular array with 8 acoustic vector sensors
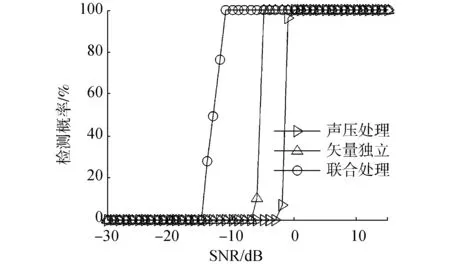
图6 声压和质点振速独立处理及其联合处理方法结果分析Fig.6 The pool experimental results of acoustic pressure process, the independent process of acoustic pressure and particle velocity, and combined processing of acoustic pressure and particle velocity
不同检测方法对比分析的检测结果如图7所示。MDL方法在噪声场中存在非均匀噪声的条件下失效;文献[8]方法与仿真实验1结果相比,其在非均匀噪声干扰的条件下性能下降;GDE方法可在信噪比大于-8 dB的条件下检测概率达到1;本文方法在信噪比大于-13 dB时检测概率为1。
综上所述,MDL方法只适用于噪声场中仅存在高斯白噪声的情况下,当噪声场中存在色噪声或非均匀噪声时估计器性能恶化甚至失效。文献[8]方法利用对角加载技术抑制了小特征值的扩散,但低信噪比下性能不佳。GDE方法鲁棒性较好,可适用于多种条件下的信源检测,但检测因子D(L)值的确定限制了GDE方法的工程实用性,本文方法低信噪比下性能优于上述3种方法,并且本文方法具有一定的鲁棒性。另外,对于各向同性噪声场圆阵接收信号的噪声特征值大小是基本相等的,而对于非均匀噪声场则接收信号噪声特征值大小存在差异,本文采用的特征值多阈值修正方法对噪声特征值进行了修正,可以一定程度地抑制噪声特征值的大小差异,所以本文算法可适用于存在非均匀噪声条件下的信源数检测。
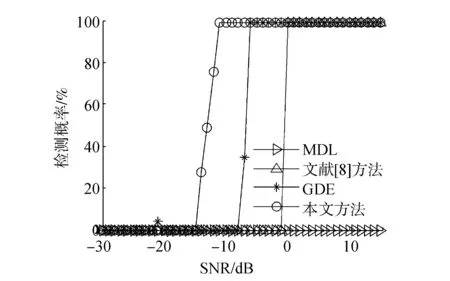
图7 不同检测方法性能实验结果分析Fig.7 The pool experimental results analysis of the detection performance of different methods
5 结论
本文基于声矢量圆阵的声压振速联合处理理论基础,并借鉴图像处理中的双阈值检测思想,提出了一种基于特征值多阈值修正的声矢量圆阵信源数检测方法:
1)理论和实验研究结果验证了该方法可以有效地提高声矢量圆阵的信源数检测性能。
2)该方法充分地将声矢量阵的良好抗噪性能与特征值多阈值修正信息论检测方法进行了有机的结合,具有更好的噪声抑制能力以及更好的目标检测性能,明显降低了可处理的信噪比门限,新方法在远程目标检测方面具有良好的性能。
[1]NEHORAI A, PALDI E. Acoustic vector-sensor array processing[J]. IEEE transactions on signal processing, 1994, 42(9): 2481-2491.
[2]HAWKES M, NEHORAI A. Acoustic vector-sensor beamforming and capon direction estimation[J]. IEEE transactions on signal processing, 1998, 46(9): 2291-2304.
[3]惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探[J]. 声学学报, 2000, 25(4): 303-307. HUI Junying, LIU Hong, YU Huabing, et al. Study on the physical basis of pressure and particle velocity combined processing[J]. Acta acustica, 2000, 25(4): 303-307.
[4]HAWKES M, NEHORAI A. Acoustic vector-sensor correlations in ambient noise[J]. IEEE journal of oceanic engineering, 2001, 26(3): 337-347.
[5]白兴宇, 姜煜, 赵春晖. 基于声压振速联合处理的声矢量阵信源数检测与方位估计[J]. 声学学报, 2008, 33(1): 56-61. BAI Xingyu, JIANG Yu, ZHAO Chunhui. Detection of number of sources and direction of arrival estimation based on the combined information processing of pressure and particle velocity using acoustic vector sensor array[J]. Acta acustica, 2008, 33(1): 56-61.
[6]白兴宇, 杨德森, 赵春晖. 基于声压振速联合信息处理的声矢量阵相干信号子空间方法[J]. 声学学报, 2006, 31(5): 410-417. BAI Xingyu, YANG Desen, ZHAO Chunhui. The coherent signal-subspace method based on combined information processing of pressure and particle velocity using the acoustic vector sensor array[J]. Acta acustica, 2006, 31(5): 410-417.
[7]贡彦飞. 基于盖尔圆准则的信源个数估计算法比较[J]. 无线电通信技术, 2002, 38(4): 57-59. GONG Yanfei. Performance comparison of source number estimation methods based on Gerschgorin disk criterion[J]. Radio communications technology, 2002, 38(4): 57-59.
[8]张杰, 廖桂生, 王珏. 对角加载对信号源数检测性能的改善[J]. 电子学报, 2004, 32(12): 2094-2097. ZHANG Jie, LIAO Guisheng, WANG Jue. Performance improvement of source number detection using diagonal loading[J]. Acta electronica sinica, 2004, 32(12): 2094-2097.
[9]杨德森, 朱中锐, 时胜国, 等. 声矢量圆阵相位模态域目标方位估计[J]. 声学学报, 2014, 39(1): 19-26. YANG Desen, ZHU Zhongrui, SHI Shengguo, et al. Direction-of-arrival estimation based on phase modal space for a uniform circular acoustic vector-sensor array[J]. Acta acustica, 2014, 39(1): 19-26.
[10]谢纪岭, 司锡才. 基于协方差矩阵对角加载的信源数估计方法[J]. 系统工程与电子技术, 2008, 30(1): 46-49. XIE Jiling, SI Xicai. Determining the number of sources based on diagonal loading to the covariance matrix[J]. Systems engineering and electronics, 2008, 30(1): 46-49.
[11]CANNY J. A computational approach to edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 1986, PAMI-8(6): 679-698.
[12]AKAIKE H. A new look at the statistical model identification[J]. IEEE transactions on automatic control, 1974, 19(6): 716-723.
[13]WAX M, KAILATH T. Detection of signals by information theoretic criteria[J]. IEEE transactions on acoustics, speech, and signal processing, 1985, 33(2): 387-392.
[14]WU H T, YANG J F, CHEN F K. Source number estimators using transformed Gerschgorin radii[J]. IEEE transactions on signal processing, 1995, 43(6): 1325-1333.
Source number detection based on multi-threshold eigenvalue correction using uniform circular acoustic vector sensor array
SHI Shengguo1,2,ZHU Wenzhao2,LI Ying2,ZHU Zhongrui1,2
(1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China; 2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)
To solve the passive detection problems of underwater remote targets, we propose a method for detecting source numbers with a uniform circular acoustic vector sensor array. First, we constructed a combined covariance matrix of the pressure and the acoustic particle velocity of the uniform circular acoustic vector sensor array. Then, based on the double-threshold detection concept, we adopted a multi-threshold image processing technology to correct the eigenvalue of the covariance matrix. Ultimately, the source number can be estimated using the information criteria approach. Results from our theoretical analyses and computer simulations show that, the proposed method can effectively improve detection performance of the infrmation criteria. The pool experimental results also demonstrate that it exhibits better detection performance and a stronger noise suppression ability than other methods,further verifying the effectiveness of our proposed method.
uniform circular acoustic vector sensor array; source detection; combined information processing of the acoustic pressure and the acoustic particle velocity; multi-threshold technology; eigenvalue correction
2015-11-15.
时间:2016-12-12.
国家自然科学基金项目(11404076);长江学者和创新团队发展计划项目(IRT-16R17).
时胜国(1973-),男,教授,博士生导师.
时胜国,E-mail:shishengguo@hrbeu.edu.cn.
10.11990/jheu.201511028
TB566
A
1006-7043(2017)01-0120-06
时胜国,祝文昭,李赢,等.基于特征值多阈值修正的声矢量圆阵信源数检测[J]. 哈尔滨工程大学学报, 2017, 38(1): 120-125. SHI Shengguo,ZHU Wenzhao,LI Ying,et al. Source number detection based on multi-threshold eigenvalue correction using uniform circular acoustic vector sensor array[J]. Journal of Harbin Engineering University, 2017, 38(1): 120-125.
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20161212.1632.038.html

