蒸散量双线性曲面回归模型的改进及验证

邵月红，刘永和，吴俊梅



蒸散量双线性曲面回归模型的改进及验证

邵月红1，刘永和2，吴俊梅3

（1. 南京信息工程大学水文气象学院，南京 210044； 2. 河南理工大学资源环境学院，焦作454000；3. 昆山市气象局，昆山 215300）

潜在蒸散发是水文循环和能量循环的一项重要组成，准确估算蒸散发对农业水资源有效利用具有重要的理论和现实意义。为获得精度稳定可靠的蒸散发估计值同时只需较少的气象资料，以沂沭河上游流域（临沂控制站）为研究区，提出改进的双线性曲面回归模型（bilinear surface regression model，BSRM）计算站点的潜在蒸散量。以实测蒸发数据折算的陆面潜在蒸散量为标准，同时以彭曼公式（P-M）为参考与之对比，检验和评价3种BSRM模型的精度，并分析各气象因子对潜在蒸散量的影响。结果表明：3种BSRM模型中，基于日照百分率、气温和相对湿度建立的双线性曲面回归模型模拟精度最高，以基于日照百分率计算的太阳辐射、气温、相对湿度建立的双线性曲面回归模型次之，以基于Hargreaves-Allen方程计算的太阳辐射、气温和相对湿度建立的双线性曲面回归模型模拟精度最差。基于日照百分率、气温和相对湿度建立的BSRM模型的模拟精度略优于P-M公式，但所需的气象因子较少，计算方法简单；且受气象因子的变化影响较少，模拟精度稳定可靠，是一种有效的替代方法。

蒸散量；气温；太阳辐射；彭曼公式（P-M）；双线性曲面回归模型（BSRM）

0 引 言

蒸散发是水文循环和能量循环的重要组成。因此，蒸散发的估算和准确测定对气候变化影响、农业水资源利用评价等都具有重要的现实意义[1-2]。签于观测的实际蒸散发的缺乏，通常由潜在蒸散发来估算实际蒸散发。目前常用的模型估算方法主要可以分为5类：水量平衡法、温度法、辐射法、质量传导法和综合法[3-4]。水量平衡法的原理清晰简单，但在实际测量中，由于土壤深层渗漏等平衡要素无法准确获得，导致实际应用中其准确率并不高[5-6]。温度法主要基于温度计算潜在蒸散发，由于只需温度这一基本气象因子，因此在资料较少的地区得到广泛应用。由于仅考虑了温度这一影响因子，估算的精度并不高，特别是在区域内潜在蒸散发受到多气象因素共同作用和影响时，模拟效果并不理想[7-8]。辐射法是基于辐射平衡建立的方法，最具代表性的是Priestley-Taylor模型（P-T）。该方法不考虑土壤热通量的影响，假设下垫面足够湿润，蒸散发量主要有辐射平衡决定。因此，假设条件成立时蒸散发模拟效果较好，反之相反[9-10]。Fisher在P-T模型的基础上进一步改进，引入了物理修正因子分别计算土壤蒸发、植被蒸发和植被截留降雨蒸发，最后求出三部分总和。虽然改进的P-T模型具有较好的模拟效果，但模型的复杂程度和所需参数的增加使其推广应用受到一定的限制[11-12]。质量传导法主要根据水汽压梯度、风速和温度建立的经验模型，实质上是彭曼模型中的干燥力。由于水表面温度及其饱和气压差未知，需要用露点温度代替水表面温度，空气温度的饱和气压差代替水表温度的气压差，会对模拟结果产生一定影响。同时需要当地的资料进行率定才能达到一定的模拟效果[13]。综合法是综合考虑了空气动力学原理和能量平衡的一种计算方法。其中最具代表性的就是Penman-Monteith模型（P-M），作为联合国粮农组织推荐的一种标准方法，其精度已在不同气候区域进行验证，得到全球广泛认可[14-16]。但P-M公式需要太阳辐射等诸多气象资料，在数据缺乏地区难以使用，很大程度上限制了该模型的实际应用。前人的研究表明不同的估算方法具有各自不同的适应性及精度，针对特定区域需要重新率定参数或进行结果修正及评估[17-19]。因此有必要研究所需资料少且精度稳定可靠的潜在蒸散发估算方法。邵月红等[17]基于区域气候模式输出的太阳辐射、温度和相对湿度构建双线性曲面回归模型来模拟蒸散量，取得了一定的效果。但是模式输出的太阳辐射与观测值又有一定程度的误差，同时大部分站点没有观测的太阳辐射使得该方法应用受到限制。本文利用沂沭河上游流域的6个气象站点的气象数据，在前期构建的双线性曲面回归模型基础上，对变量进行改进，主要通过太阳辐射与温度和日照百分率的关系来间接计算太阳辐射这个变量，同时以日照百分率直接作为变量，分3种情况来估算潜在蒸散发，并与模拟效果显著的P-M公式进行比较，以评价该模型的精度；在此基础上，进一步分析气象要素的影响，评判模型的稳定性。

1 材料与方法

1.1 研究区概况

研究区选择为沂沭河上游流域（临沂控制站），经纬度范围为：34.37°～36.38°N，117.40°～119.18°E。流域地处鲁中南低山丘陵区东南部和鲁东丘陵南部，属于暖温带半湿润季风气候区。研究区的地形主要包括平原、丘陵和山地，地势西北高东南低，最高海拔为1 125 m，水系复杂，流域空间分布如图1所示。流域内多年平均温度12 ℃左右，相对湿度约65%，水面蒸发量约839 mm。

1.2 气象数据来源

1）蒸散发数据：流域站点2006－2007年的逐日蒸散量，主要来自20 cm口径蒸发器观测仪器观测。其中费县站有20 cm口径蒸发器和E601型蒸发器同时观测蒸散发，利用费县站的2种蒸发器转换系数可以间接推算出其他5个站点的E601型蒸散发[20]。2种蒸散发转换系数在不同月份之间差异较大，首先利用一元线性回归分析拟合出各月的2种蒸散发的折算系数，然后将折算系数与20 cm口径蒸发器相乘计算出E601型蒸散发。E601型测得的蒸发量与实际水面蒸发量更为接近，以此为参考标准来检验各方法计算得到的蒸散量结果的优劣。2）其他数据：主要包括2006－2007年站点的气温（最高、最低和平均）、水汽压、风速、日照时数相关资料。沂沭河流域的莒县站有1990－2003年的实测太阳辐射资料，根据实测太阳辐射和日照时数的关系可以推算临沂子流域内6个研究站点的太阳辐射值。

1.3 蒸散量估算方法

1.3.1 改进双线性曲面回归模型

在前期构建的双线性曲面回归模型[17]基础上，对模型的太阳辐射变量进行改进。由于大部分气象站点没有观测的太阳辐射值，文中主要通过太阳辐射和日照百分率及温度的关系来间接计算太阳辐射值，再回归拟合出蒸散发量；同时将按月划分的日照百分率直接替代太阳辐射变量进行回归拟合，并与间接计算的太阳辐射回归拟合结果进行比较，进一步深入分析不同情况下的模拟精度。

蒸散发过程主要受到水分供给（由下垫面决定）、能量供给（由太阳辐射决定）和水汽输送（主要由温度、湿度和风速决定）三方面的条件控制。考虑到研究区下垫面的性质基本一致，因此蒸散量的大小主要由太阳辐射、气温、相对湿度和风速决定。研究表明[21-22]，4个气象因子对蒸散发的影响大小依次为太阳辐射、气温及相对湿度、风速。基于前3个敏感气象因子，利用性能稳定和具有自适应性的双线性曲面回归模型拟合出经验系数，由经验系数和3个气象因子可计算出不同时空上的蒸散量。双线性曲面方程[17,23-24]的基本形式为

()01·2·3··（1）

式中为日蒸散量ET0，mm/d；和为变量；0～3分别为回归系数。在第1步的BSRM中，代表太阳辐射R（MJ/(m2·d)）或者日照百分率/（%），代表相对湿度R(%)；在第2步中，变量同上，代表温度（℃）；在第3步中，分别代表第1步拟合的日蒸散量1（mm/d）和第2步拟合的日蒸散量2（mm/d）。改进双线性曲面方程进行蒸散量估算步骤如图2所示。

如图2所示，逐日蒸散量拟合步骤主要包括：1）根据ET0和R（或）、R2个因子的关系建立BSRM，按照均方差误差最小的原则拟合出其系数1～4；2）根据ET0和R（或/）、2个因子的关系建立BSRM，回归拟合出其系数1～4；最后根据ET0和上2步求出的1、2的关系再一次建立最终的BSRM模型并求其系数1～4。

本研究流域里的气象站点都属于国家二级站点，没有实测的太阳辐射数据，因此在进行BSRM拟合时，根据太阳辐射计算方式不同分3种情况考虑：

1）通过太阳辐射R和日照百分率的关系来计算太阳辐射，模型简称为BSRM，其基本公式为

R=(+·/)R（2）

式中R是大气顶太阳辐射，MJ/(m2d)；和为经验系数。

2）如果没有/时，可利用最高气温和最低气温根据Hargreaves-Allen方程[25]计算太阳辐射，模型简称为BSRM。

R=K·(max–min)0.5·R（3）

式中K是调节系数，内陆地区通常取0.17 ℃1/2，沿海地区为0.19 ℃1/2 [26]。

3）根据/和R随着季节和月份的变化呈很好的线性相关性，不计算R，直接利用/、和R进行BSRM模拟，模型简称为BSRM/N，以便与第1种情况的模拟效果进行比较。

1.3.2 修正的彭曼公式

彭曼公式是联解热量平衡方程和湍流扩散方程而导出的计算水面蒸发的理论公式，其理论基础扎实，考虑因子全面。考虑到一些因子或参数需要重新修正，本文采用修正的彭曼公式来计算蒸发量，需要气象观测资料（气温、湿度、日照、风速），其基本形式为

式中为饱和水汽压-气温关系斜率，hPa/℃；为干湿计常数；R为净短波辐射，mJ/(m2·d)；R为黑体长波辐射，mJ/(m2·d)；E为干燥力，mm/d；式中各项因子的具体计算公式参见文献[27-28]。本文中主要利用当地实测资料对P-M公式中的R和E进行修正[29]。首先利用莒县站的观测资料R和/，采用最小二乘法回归拟合求出回归方程R=（0.188+ 0.507/）·R。然后利用费县站的E-601蒸发器观测的日蒸散量和饱和差（e−e）之商同百叶箱高度的风速1.5建立回归方程=(0.204+0.1311.5)·(e−e)，根据干燥力的定义，如果将饱和水汽压差(e−e)代替饱和差(e−e)，式中的就变成干燥力E了，即E=(0.204+0.1311.5)·(e−e)，其中e为实际水汽压，hPa；e和e分别为空气温度和水面温度下的饱和水汽压，hPa。

根据图2所示的逐日蒸散量的计算流程拟合3种BRSM模型的回归系数，如表1所示。

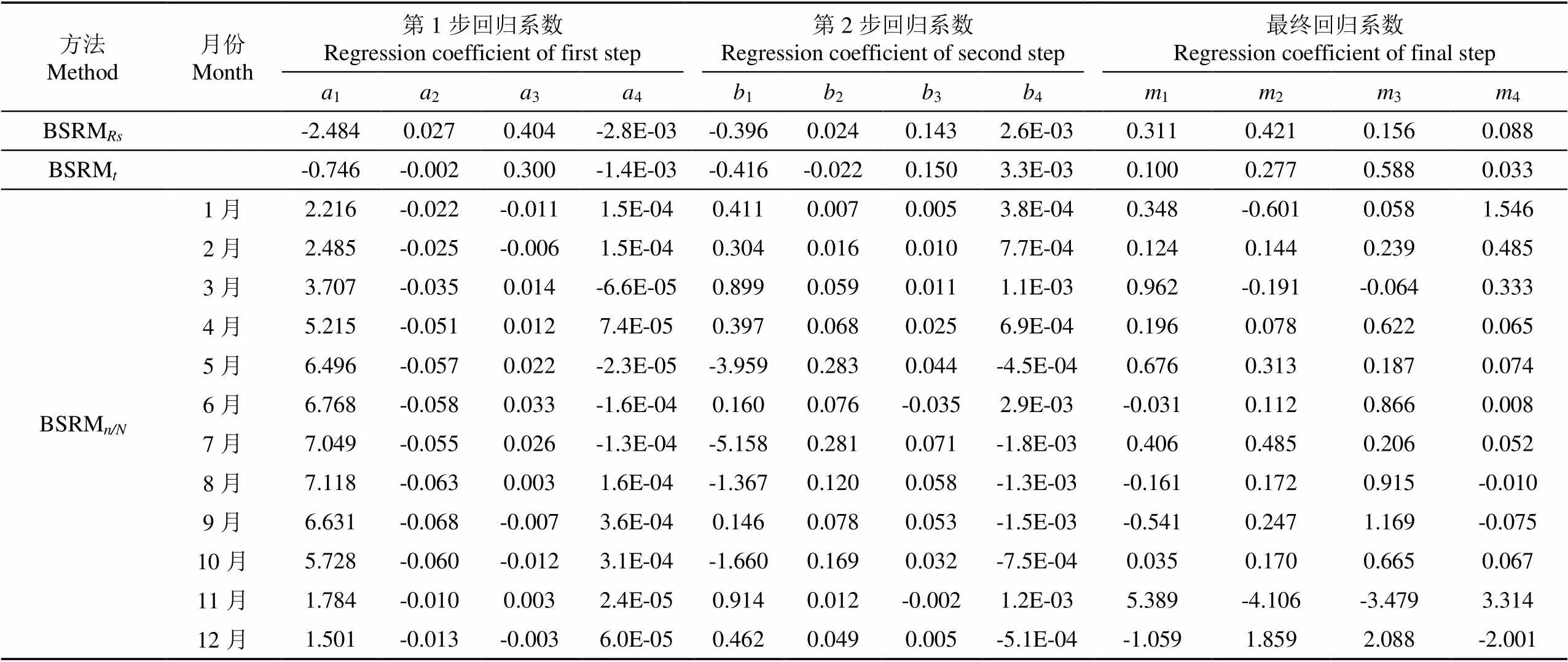
表1 基于不同气象要素获取的双线性回归模型的系数

注：BSRM基于日照百分率计算的太阳辐射、气温、相对湿度；BSRM基于Hargreaves-Allen方程计算的太阳辐射、气温、相对湿度；BSRM/N基于日照百分率、气温、相对湿度；下同。

Note: BSRMis based on relative insolation duration-based solar radiation, temperature and relative humidity; BSRMis based on solar radiation calculated by using Hargreaves-Allen equation, temperature and relative humidity; BSRM/Nis based on relative insolation duration, temperature and relative humidity; same as below.

1.4 模型比较方法

采用平均绝对偏差（mean absolute of error，MAE）、平均相对均方根差（root mean square of error，RMSE）、相关系数（）和相关曲线斜率（）4个指标评估BSRM模型的精度。4个指标可以综合反映出不同方法计算的蒸散量的精密度和准确度。具体计算公式参见文献[17,30]。在此基础上，进一步采用方差分析和检验对模拟值和观测值的均值进行差异显著性检验。

2 结果与分析

2.1 蒸散量估算方法比较

表2为沂沭河上游流域不同蒸散量方法的计算结果。由表可知，从MAE和RMSE都可以看出BSRM模拟的蒸散量的误差最小（MAE为0.48 mm、RMSE为0.64 mm），即BSRM/N模拟的蒸散量与观测的潜在蒸散量最接近，数据比较集中且精密度较高。从数据系列的相关系数来看，P-M模拟的蒸散量与观测值相关性最好，3种BRSE模型中BSRM/N的相关性最好，与P-M公式相当。相关曲线的斜率结果表明，3种BRSE模型中BSRM的模拟精度最好，斜率与1最接近；其次是BSRM/N的模拟精度，斜率小于1，存在一定程度的低估现象；BSRM的模拟效果最差，存在明显的低估现象。尽管BSRM/N的斜率显示有一定的低估，但综合考虑其他3个指标，BSRM/N模拟的蒸散量与观测蒸散量更接近，能更真好地反映蒸散量的实际情况。

表2 沂沭河上游流域不同方法计算的蒸散量比较

表3进一步分析模型模拟值与观测值的均值之间差异显著性。从表3的检验结果可知，P-M公式模拟精度较差，6个站点和站点平均都达到了0.01的显著性水平，即模拟的蒸散量和观测值的均值差异较大；其次是BSRM模型，除了沂南站点外，其他站点也都达到了0.01的显著性水平；BSRM和BSRM/N模拟精度要好于P-M公式和BSRM，大部分站点都没有通过0.05的显著性水平，即模拟值和观测值吻合的较好，但是站点间还是存在较大的差异。从站点平均来看，BSRM/N模拟精度最好。

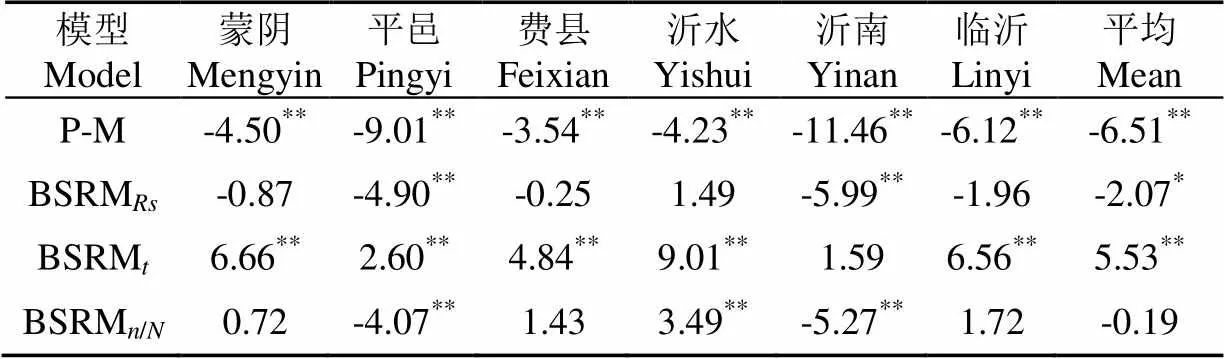
表3 不同蒸散量方法的t检验结果

注：*为通过0.05显著性检验，**为通过0.01显著性检验。

Note: * is significance at 0.05 level and ** is extreme significance at 0.01 level.

图3为流域逐日蒸散量的模拟值和观测值的比较，其中图3a和图3b为蒙阴站点P-M公式和3种BSRM模型模拟蒸散量和观测值的离散性和相关曲线斜率的比较，图3c和图3d为流域站点平均的比较。

结果表明（图3），流域站点平均的模拟效果要优于单一站点（蒙阴站）的结果，4种模型的离散性和相关曲线斜率显示P-M和BSRM/N的模拟精度要明显高于BSRM和BSRM。从相关曲线斜率来看，P-M公式优于BSRM/N的，但从散点图的离散性和趋近45°对角线（1:1线）看，P-M公式的离散度较大，特别是模拟的蒸散量在2～6 mm的范围内有一定程度的高估现象；综合来看P-M和BSRM/N2个模型模拟结果相当，与观测值相一致。3种BSRM模型中，BSRM模拟的精度最低，模拟过程不稳定、离散度较大，模拟的蒸散量比实际观测值偏低，并且误差随着蒸散增强而增大，存在明显的低估现象。低估的可能原因是模拟过程只考虑了温度这一因子，与实际过程中蒸散量受到多个因子共同主导不一致造成的。BSRM模拟的精度介于其他2种BSRM模型之间，模型同样存在不稳定问题，在低蒸散量部分模拟偏低，高蒸散量范围模拟偏高。

图4为不同方法计算的月累计蒸散量。由图可知，BSRM/N计算的月累计蒸散量与实测值最接近，特别是流域站点平均与实测值吻合很好。主要原因可能是基于R和/与月份的良好相关性建立的逐月BSRM/N模型使得整个过程的模拟精度都较高。BSRM和P-M次之，都比实测值偏高，特别是在7－9月具有明显的高估现象。其主要原因可能是：在BSRM和P-M中，R都是通过最小二乘法拟合的经验函数计算得到的，固定的经验系数对气象因子的变化敏感性较差，由较高温度计算的R和R都较大。而在现实环境中，该流域属于典型的暖温带大陆性季风气候，受副热带高压影响夏季炎热多雨，较高的湿度和较少的辐射叠加影响使得实际的潜在蒸散量并不是很大，因而造成模拟值偏高。BSRM模拟结果最差，整个过程都存在低估现象，误差随着蒸散发的增强而增大。其原因可能为：通过最高最低气温差和R的经验函数计算得到的太阳辐射较其他方法都低，而R对蒸散量的影响又是最强的，因此只把气温作为主要因子经过2次线性回归必然存在较大的误差，这与刘昌明等[21-22]的研究结果也是一致的。

2.2 气象要素影响分析

蒸散量的大小主要由太阳辐射、气温、相对湿度和风速决定，其中太阳辐射又受到日照百分率和气温等因子的影响。本研究首先给出研究区域内气温、相对湿度和风速3个气候因子之间的相互关系，接着分析日照百分率、气温、相对湿度的变化对蒸散量的影响。由图5温度和相对湿度的关系图可知，二者并不存在明显的相关性；流域的相对湿度较大，即使在温度最高的月份，大于60%的相对湿度仍占绝大部分，温度的变化对湿度的影响较小。由风速与相对湿度的相互关系可知，流域的风速强度不大，强风出现的频率较少，风速主要集中在1～3 m/s，相对湿度主要集中在50%～90%，风速的增强会减弱相对湿度的大小，但是该流域湿度较大，风速较小，基本体现不出这一变化规律。

进一步探讨日照百分率、气温、相对湿度的变化对蒸散量的影响，对3种BSRM模型精度进行评估（图6）。由于BSRM和BSRM具有相同的理论基础，在图6中只列举了精度较高的BSRM随气候因子变化产生的偏差。由图6中日照百分率的变化影响得知，通常日照百分率与太阳净辐射存在较好的正相关，太阳净辐射值随着增加而增加，进而蒸散量也随之增加。由图可知，BSRM/N受/的影响较小，无论是在阴雨天(/<33%)、多云(/为33%～67%)，还是晴天(/>67%)，模拟值都与实测值接近。BSRM受/影响较大，模拟的蒸散量随着/的减少而偏低，特别是在阴雨天时，低估程度和误差最大。其主要原因可能是BSRM模型中的太阳辐射主要通过最高最低气温差和外空辐射计算得到的，一般阴雨天的最高最低气温差较小，这样计算的R就比实际偏低，进而估测的蒸散发也偏低。图6显示在风速较大时，BSRM/N和BSRM计算的蒸散量偏差都较大。由图6中温度变化对蒸散量的影响可知，BSRM/N模拟的蒸散量受温度变化的影响较小，不管在低温还是高温，模拟的蒸散量都与实测值较接近，平均偏差较小。BSRM在温度较低的情况下模拟较好，但随着温度升高，模拟的蒸散量低估程度增加，特别是在温度>20 ℃时，存在明显的低估现象。其原因可能是随着气温升高，太阳净辐射可化为蒸散当量的数值越高，蒸散发就越强烈，同时风速增强又加速了蒸散发的过程，使得蒸散发变得就越强烈；而BSRM模拟的蒸散量主要取决于温度这一因子，经过经验公式得到的固定经验系数对温度的敏感性不够，模拟的蒸散量整体偏低，低估程度随着蒸散发增强而增大。

由图6中相对湿度变化对蒸散量的影响可知，2种BSRM模型都是在相对湿度高的情况下模拟效果较好。相对于BSRM而言，BSRM/N受相对湿度变化的影响较小，模拟值与实测值接近。在相对湿度较小（<50%）且风速较大时，2种模型模拟都存在一定程度的低估，可能原因是相对湿度和风速的叠加效应，加剧了蒸散发；而BSRM模型只考虑气温因子并经过2次线性回归得到的固定经验系数对外界变化激烈的环境因子的敏感性较差，因而模拟的蒸散量要低于实际值。

综上可知，BSRM/N模型模拟值与观测值相一致，模拟效果受日照百分率、气温和相对湿度的变化影响较小，模拟精度稳定可靠；BSRM模型不稳定，受日照百分率等因子的变化影响较大，随着因子的变化呈现不同程度的低估现象。只有大的风速伴随高温干燥的天气时，才会对蒸散发产生明显的影响。

3 结论与讨论

蒸散发方法估算结果表明，在3种BSRM模型中，BSRM/N模拟精度最高，BSRM次之，BSRM最差。BSRM/N模拟的蒸散量的准确度略低于P-M公式，但精密度要高于P-M；检验表明P-M公式和BSRM模拟效果较差，存在0.01的显著性差异；从月蒸散量的模拟来看，BSRM/N与实测值最接近。综合来看，BSRM/N模拟精度要略优于P-M公式。

主要气象要素影响分析表明，BSRM/N法受主要气象要素的影响最小，模拟的蒸散量几乎不随日照百分率、气温和相对湿度的变化而变化，BSRM次之，BSRM受其影响最大，在较低的日照百分率、相对湿度和较高的气温下，模拟的蒸散量有明显的低估现象，并且这一现象随着风速增强而加剧。

BSRM/N相比P-M而言，所需的气象因子较少，计算方法简单，受气象因子的变化影响小，模拟精度稳定可靠，其精度与P-M相当，是一种比较有效的替代方法。3种BSRM模型中，首选BSRM/N，其次BSRM，如果没有日照数据时，可参考BSRM。

[1] 杨邦，任立良，王贵作，等. 基于水文模型的流域蒸散发规律[J]. 农业工程学报，2009，25(增刊2)：18－22.

Yang Bang, Ren Liliang, Wang Guizuo, et al. Estimaton of evapotranspiration in catchment based on distributed watershed hydrological model[J]. Transactions of the Chinese Society of Agricultural ngineering (Transactions of the CSAE), 2009, 25(Suppl 2): 18－22. (in Chinese with English abstract)

[2] 赵玲玲，夏军，许崇育，等. 水文循环模拟中蒸散发估算方法综述[J]. 地理学报，2013，68(1)：127－136.

Zhao Lingling, Xia Jun, Xu Chongyu, et al. A review of evapotranspiration estimation methods in hydrological models[J]. Acta Geographica Sinica, 2013, 68(1): 127－136. (in Chinese with English abstract)

[3] Xu C Y, Singh V P. Evaluation and generalization of temperature-based methods for calculating vaporation[J]. Hydrological Processes, 2001, 15: 305－319.

[4] 陶新娥，陈华，许崇育. 潜在蒸散发公式2种修正方法及其在闽江流域的应用研究[J]. 亚热带资源与环境学报，2014，9(3)：12－19.

Tao Xin’e, Chen Hua, Xu Chongyu. Potential evapotranspiration equations: Two modification methods and their application in Minjiang river basin[J]. Journal of Subtropical Resources and Environment, 2014, 9(3): 12－19. (in Chinese with English abstract)

[5] Allen R G, Pereira L, Howell T A, et al. Evapotranspiration information reporting: Factors governing measurement accuracy[J]. Agricultural Water Management, 2011, 98(6): 899－920.

[6] 宋璐璐，尹云鹤，吴绍洪. 蒸散发测定方法研究进展[J]. 地理科学进展，2012，13(9)：1186－1195.

Song Lulu, Yin Yunhe, Wu Shaohong. Advancements of the metrics of evapotranspiration[J]. Progress in Geography, 2012, 13(9): 1186－1195. (in Chinese with English abstract)

[7] 张晓琳，熊立华，林琳，等. 五种潜在蒸散发公式在汉江流域的应用[J]. 干旱区地理，2012，35(2)：229－237.

Zhang Xiaolin, Xiong Lihua, Lin Lin, et al. Application of five potential evapotranspiration equations in Hanjiang Basin[J]. Arid Land Geography, 2012, 35(2): 229－237. (in Chinese with English abstract)

[8] 刘晓英，李玉中，王庆锁. 几种基于温度的参考作物蒸散量计算方法评价[J]. 农业工程学报，2006，22(6)：12－18.

Liu Xiaoying, Li Yuzhong, Wang Qingsuo. Evaluation on several temperature-based methods for estimating reference crop evapotranspiration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(6): 12－18. (in Chinese with English abstract)

[9] Priestley C H B, Taylor R J. On the assessment of surface heat flux and evaporation using large scale parameters[J]. Monthly Weather Review, 1972, 100(2): 81－92.

[10] 赵捷，徐宗学，左德鹏，等. 基于辐射的潜在蒸散发量估算方法在黑河流域的适用性分析[J]. 干旱区资源与环境，2013，27(10)：107－114.

Zhao Jie, Xu Zongxue, Zuo Depeng, et al. Radiation-based methods to estimate potential vapotranspiration in the Heihe River basin[J]. Journal of Arid Land Resources and Environment, 2013, 27(10): 107－114. (in Chinese with English abstract)

[11] Fisher J B, Tu K P, Baldocchi D D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-Ⅱdata, validated at 16 FLUXNET sites[J]. Remote Sensing of Environment, 2008, 112(3): 901－919.

[12] Vinukollu R K, Wood E F, Ferguson C R, et al. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches[J]. Remote Sensing of Environment, 2011, 115(3): 801－823.

[13] Singh V P, Xu C Y. Sensitivity of mass-transfer-based evaporation equations to errors in daily and monthly input data[J]. Hydrological Processes, 1997, 11: 1465－1473.

[14] Allen R G, Pereira L S, Raes D, et al. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirement[M]. Irrigation and Drainage Pape 56. Rome: FAO, 1998.

[15] 王海波，马明国. 基于遥感和Penman-Monteith 模型的内陆河流域不同生态系统蒸散发估算[J]. 生态学报，2014，34(19)：5617－5626.

Wang Haibo, Ma Mingguo. Estimation of transpiration and evaporation of different ecosystems in an inland river basin using remote sensing data and the Penman-Monteith equation[J]. Acta Ecologica Sinica, 2014, 34(19): 5617－5626. (in Chinese with English abstract)

[16] Ershadi A, McCabe M F, Evans J P, Wood E F. Impact of model structure and parameterization on Penman–Monteith type evaporation models[J]. Journal of Hydrology, 2015, 525: 521－535.

[17] 邵月红，张万昌，刘永和，等. 利用区域气候模式RIEMS产品分析日蒸散量及其影响[J]. 高原气象，2012，31(4)：983－992.

Shao Yuehong, Zhang Wanchang, Liu Yonghe, et al. Daily Evapotranspiration calculated with RIEMS model output and its effect[J]. Plateau Meteorology, 2012, 31(4): 983－992. (in Chinese with English abstract)

[18] Westerhoff R S. Using uncertainty of Penman and Penman-Monteith methods in combined satellite and ground-based evapotranspiration estimates[J]. Remote Sensing of Environment, 2015, 169: 102－112.

[19] Ershadi A, McCabe M F, Evans J P, et al. Multi-site evaluation of terrestrial evaporation models using FLUXNET data[J]. Agricultural and Forest Meteorology, 2014, 187: 46－61.

[20] 盛琼，申双和，顾泽. 小型蒸发器的水面蒸发量折算系数[J].南京气象学院学报，2007，30(4)：561－565.

Sheng Qiong, Shen Shuanghe, Gu Ze. Conversion coefficient between small evaporation pan and theoretically calculated water surface Evaporation in China[J].Journal of Nanjing Institute of Meteorology, 2007, 30(4): 561－565. (in Chinese with English abstract)

[21] 刘昌明，张丹. 中国地表潜在蒸散发敏感性的时空变化特征分析[J]. 地理学报，2011，66(5)：579－588.

Liu Changming, Zhang Dan. Temporal and spatial change analysis of the sensitivity of potential evapotranspiration to meteorological influencing factors in China[J]. Acta Geographica Sinica, 2011, 66(5): 579－588. (in Chinese with English abstract)

[22] 杨林山，李常斌，王帅兵，等. 洮河流域潜在蒸散发的气候敏感性分析[J]. 农业工程学报，2014，30(11)：102－109.

Yang Linshan, Li Changbin, Wang Shuaibing, et al. Sensitive analysis of potential evapotranspiration to key climatic factors in Taohe River Basin[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(11): 102－109. (in Chinese with English abstract)

[23] Alexandris S, Kerkides P, Liakatas A. Daily reference evapotranspiration estimates by the ‘‘Copais’’ approach[J]. Agricultural Water Management, 2006, 82: 371－386.

[24] Chatzithomas C D, Alexandris S. Solar radiation and relative humidity based, empirical method, toestimate hourly reference evapotranspiration[J]. Agricultural Water Management, 2015, 152: 188－197.

[25] Gavilán P, Lorite I J, Tornero S, et al. Regional calibration of Hargreaves equation for estimating reference ET in a semiarid environment[J]. Agricultural Water Management, 2006, 81: 257－281.

[26] 刘钰，Pereira L S. 气象数据缺测条件下参照腾发量的计算方法[J]. 水利学报，2001(3)：11－17.

Liu Yu, Pereira L S. Calculation methods for reference evapotranspiration with limited weather data[J]. Journal of Hydraulic Engineering, 2001(3): 11－17. (in Chinese with English abstract)

[27] 王书功，康尔泗，金博文，等. 黑河山区草地蒸散发量估算方法研究[J]. 冰川冻土，2003，25(5)：558－565.

Wang Shugong, Kang Ersi, Jing Bowen, et al. A Study of estimation of evapotranspiration on grass land in the mountains of Hei river basin[J]. Journal of Glaciology and Geocryology, 2003, 25(5): 558－565. (in Chinese with English abstract)

[28] 赵丽雯，吉喜斌. 基于FAO-56双作物系数法估算农田作物蒸腾和土壤蒸发研究—以西北干旱区黑河流域中游绿洲农田为例[J]. 中国农业科学，2010，43(19)：4016－4026.

Zhao Liwen, Ji Xibin. Quantification of transpiration and evaporation over agricultural field using the FAO-56 dual crop coefficient approach-a case study of the maize field in an oasis in the middle stream of the Heihe river basin in Northwest China[J]. Scientia Agricultura Sinica, 2010, 43(19): 4016－4026. (in Chinese with English abstract)

[29] John D V. Simplified versions for the Penmanevaporation equation using routine weather data[J]. Journal of Hydrology, 2006, 331: 690－702.

[30] 邵月红，林炳章，叶金印，等. 基于Elman 动态神经网络的降雨-径流模拟研究[J]. 大气科学学报，2014，37(2)：223－228.

Shao Yuehong, Lin Bingzhang, Ye Jinyin, et al. Application of rainfall-runoff simulation based on Elman recurrent dynamic neural network model[J]. Transactions of Atmospheric Sciences, 2014, 37(2): 223－228. (in Chinese with English abstract)

Improvement and validation of bilinear surface regression model for daily evapotranspiration estimation

Shao Yuehong1, Liu Yonghe2, Wu Junmei3

(1.210044,;2.454000,;3.215300,)

The accurate estimation of potential evapotranspiration (ET0) is an important content of hydrological cycle and flux cycle, which has an important theoretical and practical significance for effective use of agricultural water resources in the context of climate change. In order to acquire stable and reliable estimation method of evapotranspiration that need only a small number of climatic factors, an improved ET0estimation method of bilinear surface regression model (BSRM) was used to calculate the daily evapotranspiration based on the observed meteorological data from 6 weather stations in the upper Yishu River watershed (34.37°-36.38°N, 117.40°-119.18°E). Three types of BSRM models were considered according to the difference in computing solar radiation in this study. In the first method, the relative insolation duration and the ET0estimation was based on the calculated solar radiation, relative humidity and air temperature (BSRM/N). In the second method, relative humidity, air temperature and solar radiation computed by relative insolation duration and extra-terrestrial radiation were used for ET0estimation (BSRM). In the third method, three variables of solar radiation computed by Hargreaves-Allen equation, relative humidity and air temperature were used for ET0estimation (BSRM). Meanwhile, Penman-Monteith (P-M) equation was used to estimate the ET0as a reference and comparison method. The precision of the 3 kinds of BSRM approaches was tested and evaluated based the standard of land surface potential ET0calculated by the means of conversion coefficient and observed evapotranspiration. On the base of above studies, the influential factors of ET0were further analyzed. The results showed that the model precision forET0estimation was highest in BSRM/N, followed by BSRMand BSRM. The BSRM/Nmethod has the minimum mean absolute of error and root mean square of error (0.48 and 0.64 mm). The P-M equation and BSRM/Nmethod could yield the reliable ET0estimation, however the P-M equation could overestimate the results in daily ET0between 2-6 mm. The general tendency of ET0estimation from the 3 kinds of BSRM methods and P-M equation were consistent with that of the observation for monthly ET0, while the accuracy of ET0from BSRM/Nwas closer to the observation. Studying the impacts of major meteorological factors on ET0showed that the BSRM/Nmethod had the least effect on the ET0, followed by BSRMand BSRMmethod. The simulated ET0from the BSRM/Nmethod was in accordance with the observed value at various relative insolation duration, relative humidity and air temperature. The underestimation and bias from BSRMincreased at the higher temperature, the lower relative insolation duration and relative humidity. The stronger wind speeded up the process of evapotranspiration. The estimated precision from the BSRM/Nmodel was slightly higher than the P-M model, and the former was little influenced by meteorological factors. The input meteorological variables were relatively less and convenient to obtain, which suggested that the proposed BSRM/Nmodel may become a stable and reliable alternative for routine daily evapotranspiration estimation in the study area.

evapotranspiration; temperature; radiation; Penman-Monteith model; Bilinear surface regression model (BSRM)

10.11975/j.issn.1002-6819.2017.02.013

P426.2

A

1002-6819(2017)-02-0094-08

2016-04-01

2016-09-10

国家自然科学基金（41105074）；江苏省自然科学基金项目（BK20141001）；淮河流域气象开放基金（HRM201502）；江苏省气象局青年科研基金项目资助（Q201602）。

邵月红，女，山西侯马人，讲师，博士，研究方向为水文统计、水文气象及其应用。南京 南京信息工程大学水文气象学院，210044。 Email：syh@nuist.edu.cn

邵月红，刘永和，吴俊梅. 蒸散量双线性曲面回归模型的改进及验证[J]. 农业工程学报，2017，33(2)：94－101. doi：10.11975/j.issn.1002-6819.2017.02.013 http://www.tcsae.org

Shao Yuehong, Liu Yonghe, Wu Junmei. Improvement and validation of bilinear surface regression model for daily evapotranspiration estimation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 94－101. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.02.013 http://www.tcsae.org