基于QG-SA算法的纯电动公交动力系统参数优化

曾禹乔 刘平 徐琪

（西南交通大学，成都 610031）

基于QG-SA算法的纯电动公交动力系统参数优化

曾禹乔 刘平 徐琪

（西南交通大学，成都 610031）

为提高纯电动公交车的爬坡性能、加速性能以及续驶里程，通过AVL_Cruise建立了双轴双电机驱动的纯电动公交车模型，结合量子遗传算法和模拟退火算法的优点，提出了一种QG-SA算法对纯电动公交车的动力系统参数进行了优化。结果表明，与模拟退火算法相比，QG-SA算法不仅缩短了优化时间，且优化效果更好，有效改善了纯电动公交车的动力性和经济性。

1 前言

纯电动公交车的爬坡性能、加速性能以及续驶里程等与其动力系统的参数配置有着紧密的联系，因此需要对其动力系统参数进行优化。动力系统参数优化属于非线性、不连续的优化问题[1]，可采用模拟退火算法（Simulated Annealing，SA）进行优化，但此方法优化速度较慢。随着量子计算的发展，研究者着手将量子遗传算法（Quantum GeneticAlgorithm，QGA）与其它的智能算法相结合以改进该算法的性能，但是在面对复杂的优化问题时，量子遗传算法也存在陷入局部最优的缺陷。本文针对此优化问题，结合模拟退火算法与种群规模小、计算速度快、效率高的量子遗传算法的优点提出了一种QG-SA算法，并利用该算法对纯电动公交车的动力系统参数进行了优化，进而提高了纯电动公交车的动力性和经济性。

2 优化模型的建立

2.1 整车模型的建立

所研究的纯电动公交车动力系统采用双电机双轴驱动的方式，即前/后轴电机、离合器和驱动桥均采用组合驱动方式，其结构如图1所示。本文利用AVL_Cruise建立纯电动公交车模型进行仿真，整车仿真模型如图2所示，模型参数见表1。

图l双电机双轴驱动的纯电动公交车结构示意

图2 纯电动公交车整车模型

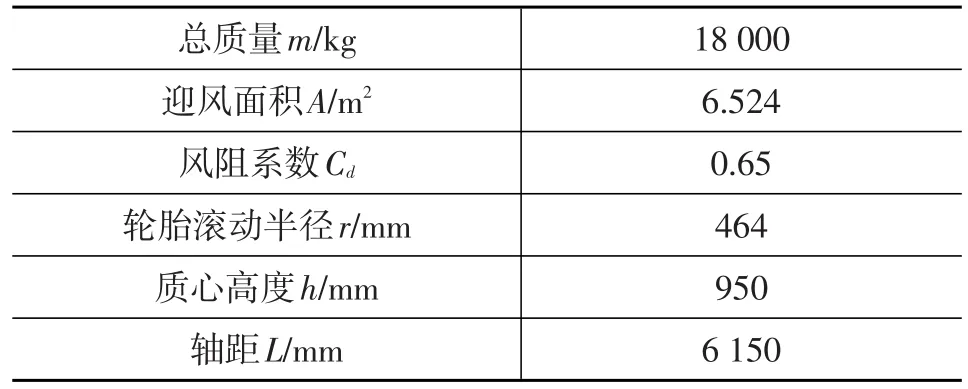
表1 纯电动公交车整车模型参数

2.2 优化目标建立

对纯电动公交车的动力系统参数进行优化需要考虑其动力性和经济性，本文利用爬坡度和加速时间评价动力性，利用续驶里程评价经济性。采用权重系数法建立优化目标函数：

式中，p和e分别为动力性和经济性权重因子；α、β和γ分别为爬坡度、加速时间和续驶里程权重因子；分别为爬坡度、加速时间和续驶里程。

本文采用的优化参数包括前/后电机的峰值转速和额定转速、前/后主减速器速比及电池容量。

3 QG-SA优化算法实现原理

QG-SA优化方法的核心思想是综合运用模拟退火算法和量子遗传算法的优点，设置一定的边界条件，从而既提高优化速度，又可实现全局最优。

3.1 模拟退火算法

模拟退火算法是基于Monte-Carlo迭代求解策略的一种随机寻优算法，该算法来源于固体退火过程，包括加温、等温和降温三部分。首先将固体加热到足够高的温度，加强粒子的热运动，消除之前存在的非均匀状态。然后缓慢降温，分子以低能状态排列，当分子能量达到最低时，系统达到稳定[2，3]。

当温度为T时，分子处于i状态的概率满足如式（2）的Boltzmann分布[2]：

式中，Ei表示处于i状态的能量；k表示玻尔兹曼常数。

由式（2）可知，模拟退火算法的基本思想为首先设置一个初始温度，随着温度的逐渐降低至最低温度，分子停留在低能量状态的概率增大，当温度趋近于0时，随机搜索过程以概率1停在最优解。为保证系统状态有充足的时间在每个温度下达到平衡，温度下降的速度需要足够缓慢。起始温度和温度下降系数是高质量解的关键参数。

3.2 量子遗传算法

量子遗传算法首先将量子比特几率幅应用于染色体编码使染色体可以表达为多个状态，以增加种群的多样性，使算法能在较小的种群规模下求得最优解，然后利用量子门更新染色体达到寻求最优解的目的[4]。

3.3 QG-SA优化算法

3.3.1 基本思想

QG-SA算法分为两个阶段：第1阶段是通过量子遗传算法对问题进行优化求解，通过这一阶段可以寻找到一个适应度较高的种群；第2阶段是将适应度较高的种群作为模拟退火算法的初始值，使模拟退火算法拥有一个好的初始状态从而缩短优化时间。

3.3.2 量子遗传算法终止条件

为保证量子遗传算法能给模拟退火算法提供一个较优的初始值，需要设置一个合适的终止条件。本文编写的量子遗传算法的终止条件由最开始设定的最大进化代数、连续n代的最大适应度和平均适应度共同决定。因为实际运行时，代数越大适应度值也逐渐增大，当代数足够大时适应度值趋于稳定，相邻两代的适应度差值也保持在一定范围内，此时种群的适应度较高。因此考虑在允许的最大代数内，当连续n代的最大适应度和平均适应度基本保持不变时作为算法的终止条件，即

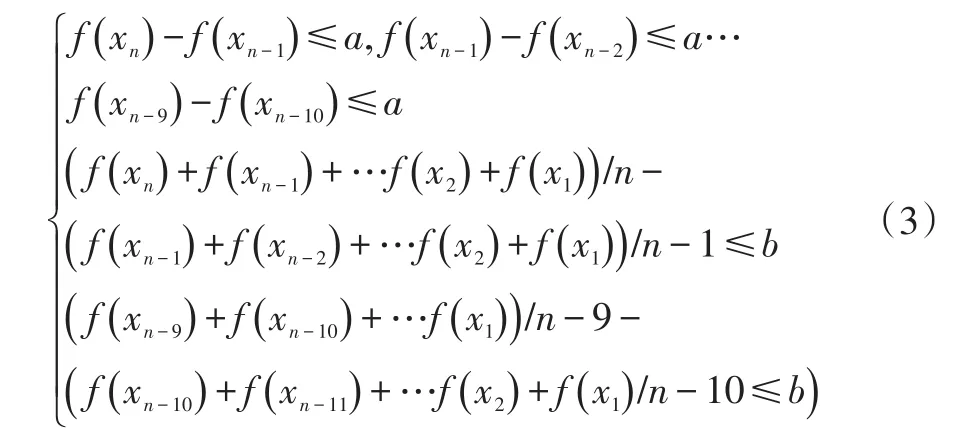
3.3.3 算法实现

利用QG-SA算法对动力系统参数进行优化的流程如图3所示。首先通过量子遗传算法进行优化，若满足终止条件则为较优解；否则，一直计算直至达到最大代数时终止计算。然后将量子遗传算法求得的解作为模拟退火算法的初始值，再运行模拟退火算法求得全局最优解。

图3 优化流程

量子遗传算法通过Matlab编写，实现原理如下[5]：

a.初始化种群，随机生成n个以量子比特为编码的染色体。

b.对初始化种群的每个个体进行测量，得到对应的确定解，该解为二进制串，串长由优化参数的精度决定，经计算本文将所有参数的串长取为17。

c.通过式（1）对确定解进行适应度评估，并记录最优个体和适应度。

d.判断是否满足终止条件，若满足则退出；否则量子门更新种群。本文将连续10次相邻两代的最大适应度的差小于a及平均适应度的差小于b作为量子遗传算法终止计算的条件，a、b分别取为0.01、0.01。

e.重复步骤a～d，满足终止条件或达到最大代数时结束计算。

模拟退火算法是将AVL_Cruise与Isight相结合来实现动力系统参数优化，为使最终得到的解为最优解，将起始温度设置为1，退火系数设置为0.9。进行优化计算时，将基于AVL_Cruise建立的车辆动态分析模型作为后台软件运行，与Isight软件通过联合仿真实现优化数据的更新。

4 仿真结果分析

量子遗传算法主要用于对模拟退火算法进行优化，因此分别采用QG-SA算法和模拟退火算法对动力系统参数进行优化对比分析。两种算法的进化过程见图4，纯电动公交车动力系统参数优化前、后对比结果见表2，参数优化前、后整车车性能对比结果见表3，其中动力性用公交车车速由0增加到25 km/h和由车速0增加到50 km/h时的加速时间和爬坡度来表征，经济性用续驶里程来表征。

图4 两种算法的进化过程

表3 动力参数优化前、后纯电动公交车性能对比

由图4可看出，经过200代的计算，QG-SA算法从91代已经开始收敛，远小于模拟退火算法开始收敛的代数，由此可知，QG-SA算法通过量子遗传算法求得一个较优解作为模拟退火算法的初始值可大大提高模拟退火算法寻找全局最优值的速度。

由表3可知，采用QG-SA算法进行参数优化后，在车速由0增加到25 km/h时的加速时间减少了0.2 s，在车速由0增加到50 km/h时的加速时间减少了0.46 s，最大爬坡度增加了4.43%，续驶里程增加了32.700 57 km；当采用模拟退火算法进行优化后，在车速由0增加到25 km/h时的加速时间减少了0.2 s，在车速由0增加到50 km/h时的加速时间减少了0.46 s，最大爬坡度增加了4.37%，续驶里程增加了13.580 24 km。优化结果表明，两种算法对纯电动公交车的动力性和经济性均有所改善，但是采用QG-SA算法优化后，该车的续驶里程增加的更长，即对改善该车的经济性效果更好。

图5、图6分别为在1个NEDC循环工况下，纯电动公交车动力系统参数优化前、后的SOC对比曲线和电机效率对比曲线。

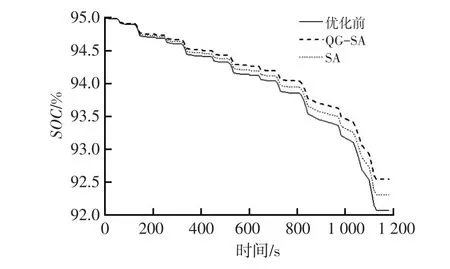
图5SOC曲线

图6 电机效率曲线

从图5可看出，在初始电量相同的情况下，采用两种算法优化后的SOC曲线都比优化前的SOC曲线高，表明优化后电量消耗减少，经济性有所提高；由图6可看出，利用两种算法优化后，电机效率在大部分工作点大于优化前，提高了电机在高效率区域工作的可能性。从上述结果可知，采用两种算法对纯电动汽车动力系统参数进行优化均可有效改善电池能量消耗和电机效率，且QG-SA算法对电池能量消耗和电机效率改善最好。

5 结束语

为了能使纯电动公交车发挥出最佳的动力性和经济性，本文通过AVL_Cruise建立了双轴双电机驱动的纯电动公交车模型，结合量子遗传算法和模拟退火算法优点提出了一种QG-SA算法，利用QG-SA算法对纯电动公交车的动力系统参数进行了优化。通过对仿真结果的分析表明，QG-SA算法不仅提高了模拟退火算法的收敛速度，也改善了纯电动公交车的经济性和动力性，并且起到了比模拟退火算法更好的效果，因此QGSA算法可作为一种新的公交车辆动力系统优化方法。

1 张佩佩.基于量子遗传算法的Plug-in混合动力汽车的匹配优化研究.内燃机，2014（6）:29～32，36.

2 Dao T T,Zelinka I,Duy V H.Use of Simulated Annealing for Adaptive ControlSystem.International Journal of Energy Optimization&Engineering,2013,2（3）:42～54.

3 M.Locatelli.Convergence of a Simulated Annealing Algo⁃rithm for Continuous Global Optimization.Journal of Global Optimization,2000,183.

4 梁昌勇,柏桦,蔡美菊,等.量子遗传算法研究进展.计算机应用研究,2012,29（7）:2401～2405.

5 吴凇,陈钢.改进量子遗传算法在电机结构优化中的应用.鱼雷技术,2015（1）:49～54.

（责任编辑 文 楫）

修改稿收到日期为2016年7月13日。

Power System Parameters Optimization of Electric Transit Bus Based On QG-SA Algorithm

Zeng Yuqiao,Liu Ping,Xu Qi
（Southwest Jiaotong University,Chengdu 610031）

To improve gradeability,accelerating ability and driving range of electric transit bus,an electric transit bus model driven by double-shaft dual-motor was built with AVL Cruise,and a QG-SA algorithm was proposed to optimize power system parameters of this bus based on advantages of quantum genetic algorithm and simulated annealing algorithm.The results show that,compared with simulated annealing algorithm,QG-SA algorithm not only shortens optimization time, but also has better optimization effect,moreover,it improves power performance and economy of electric transit bus.

Electric transit bus,Power system parameter,Optimization

纯电动公交车 动力系统参数 优化

U469.72

A

1000-3703（2017）01-0048-04