改化的有理函数模型在卫星影像定位中的应用

王鹏生，贺少帅，刘排英

（1.石家庄铁路职业技术学院 测绘工程系，河北 石家庄 050041；2. 中国航天空气动力技术研究院，北京 100074）

改化的有理函数模型在卫星影像定位中的应用

王鹏生1，贺少帅2，刘排英1

（1.石家庄铁路职业技术学院 测绘工程系，河北 石家庄 050041；2. 中国航天空气动力技术研究院，北京 100074）

近年来，鉴于高分辨率卫星传感器参数的保密性和构建模型的复杂性常使用有理函数模型进行高分辨率卫星高精度几何定位。但是，在解算有理函数模型参数时，在影像的行和列方向上会产生较大的系统误差，从而影响几何定位精度。因此，提出了一种基于像方坐标系的有理函数优化模型，并将其用于IRS-P5立体像对几何定位。结果表明，在地形较复杂的地区定位效果改善明显，可将该模型推广用于实现高分辨率卫星影像高精度几何定位。

有理函数模型；仿射变换；优化模型；立体影像；几何定位

1 RPC优化模型

1.1 RPC模型[5]

RPC 模型是关于地面点空间坐标(X,Y,Z)与其对应的像点坐标(r,c)的比值多项式。在实际应用中，往往将地面坐标和像点坐标正则化或标准化（平移和缩放）到-1～1之间，从而增强参数求解的稳定性，对于一景影像，比值多项式定义为：

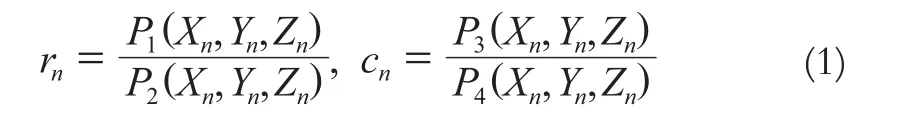
式中，(Xn,Yn,Zn)为正则化的地面点坐标；(rn,cn)为正则化的像点坐标。由于RPC模型是独立于像点和地面点坐标系统的，即可选用任意像点和地面点坐标系统。对于卫星遥感影像，一般是根据实际需要（如高斯坐标、大地坐标等坐标系统）选用像点坐标和对应的地面坐标系。有理函数的分子、分母具有相同的形式和阶次，多项式P1、P2、P3、P4为：

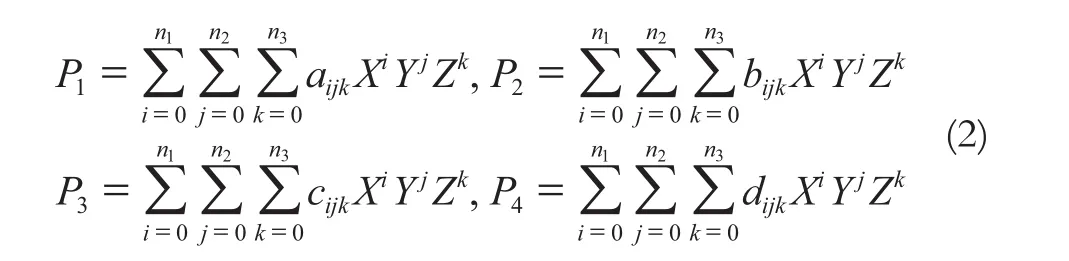
多项式的系数幂满足的条件为：0≤n1≤3，0≤n2≤3，0≤n3≤3且n1+n2+n3=3。每个多项式P1、P2、P3、P4都是包含了20个系数的三次多项式且满足：

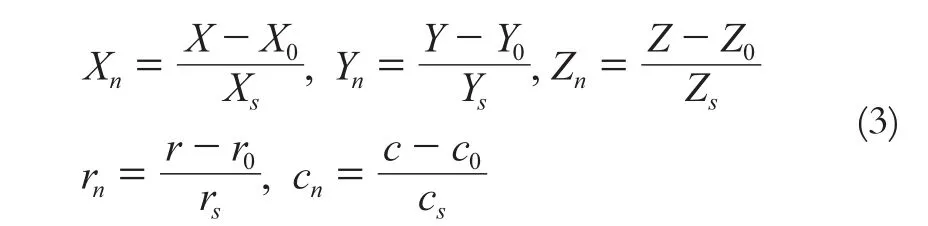
式中，X0、Y0、Z0、Xs、Ys、Zs为地面坐标的正则化平移和比例参数；r0、c0、rs、cs为像点坐标的正则化平移和比例参数；aijk、bijk、cijk、dijk为多项式系数，且b0、d0通常取值为1。正则化参数与RPC模型4个多项式的80个系数组成影像的辅助参数RPC文件。

1.2 RPC参数的优化方法[6-8]

由于RPC模型存在系统误差会影响解的稳定性，若直接使用则大大降低了卫星遥感影像的几何定位精度，因此需要通过优化RPC模型来提高卫星影像几何定位精度。

对于窄视场角的CCD推扫式传感器，系统误差主要体现在影像的行向和列向，可通过定义在影像像面的仿射变换模型来减小行向和列向的系统误差，优化模型为：

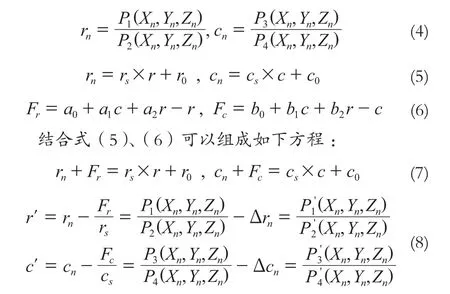
将原始RPC模型的ak替换为ak−∆Lnbk，ck替换为ck−∆Sndk(k=1,2,3,…,20)，从而消除RPC系统误差，其中(x, y)为控制点在影像面的量测坐标，(s,l)为控制点利用RPC模型的地面坐标投影值，该变换参数和RPC模型参数一起等同于严格成像几何模型的卫星系统参数。该方法简单有效，能在得到影像的原始RPC系数之后，通过对新增GCPs的计算和影像坐标量测得到计算坐标和量测坐标之间的仿射变换系数从而解求出更为精确的行列坐标(S ',L')，达到优化的目的。

2 实验及分析

2.1 实验数据

实验选择2 m正射影像和30 m ASTER高程模型作为平面和高程控制资料，对2景IRS-P5立体影像进行正射校正。

2.2 实验方法

实验通过IRS-P5影像附带的RPC参数文件，构建有理函数立体定位模型，并结合少量（9个）地面控制点对立体像对进行几何定位。由于卫星影像获取时受诸多因素（大气折射、地球曲率、地形起伏、传感器平台稳定性等）影响，使得影像存在较大的变形，因此可采用基于仿射变换的优化模型，以提高影像的几何定位精度。实验数据立体像对1（2006-10-29成像）、立体像对2（2006-09-26成像）对应的地面控制点分布如图1所示。

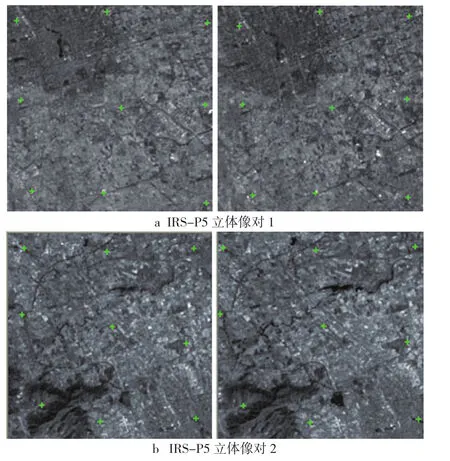
图1 立体像对地面控制点分布图

通过已知的RPC参数文件构建立体定位模型，并使用9个地面控制点完成绝对定向。地面控制点的中误差如表1所示。优化模型IRS-P5立体像对仿射变换系数如表2所示。

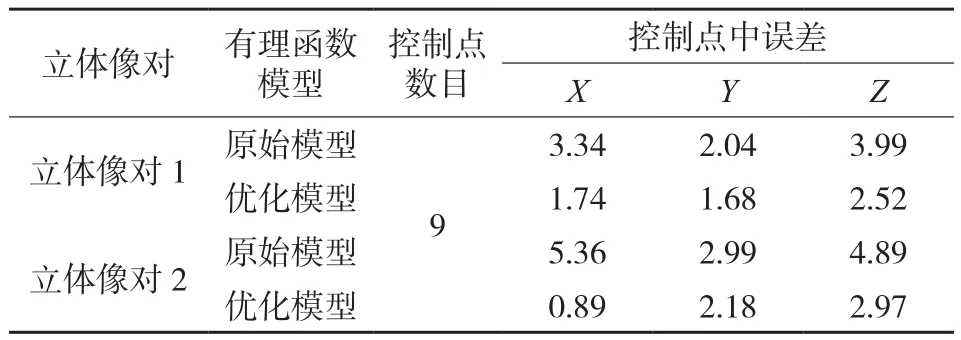
表1 IRS-P5立体像对地面控制点中误差/m

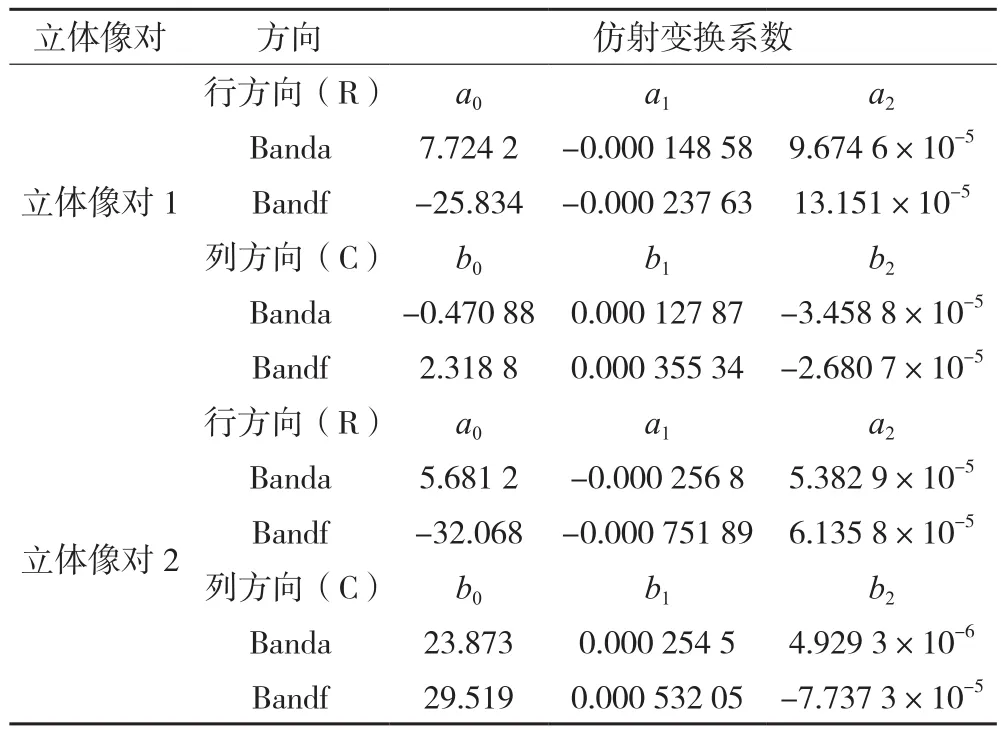
表2 优化模型IRS-P5立体像对仿射变换系数

2.3 实验结果

为了评价优化的RPC定位模型应用于IRS-P5影像立体像对的几何定位精度，可采用目视定性检查和计算检查点较差中误差定量检查相结合的方法。

2.3.1 目视检查

目视检查是将正射影像与参考影像在Erdas9．2窗口中进行卷帘操作观测特征地物的吻合度。图2是立体像对1对应的正射影像的城区河流及城市道路，图3是立体像对2对应的正射影像的城区河流及山间道路。

图2 IRS-P5立体像对1正射影像特征地物叠合目视检查图

图3 IRS-P5立体像对2 正射影像特征地物叠合目视检查图

2.3.2 定量检查

分别在IRS -P5正射影像和参考影像上选择均匀分布的20个地面检查点，计算较差中误差以评价卫星影像的几何定位精度，评价结果如表3所示。

表3 IRS-P5立体像对正射影像平面控制点中误差/m

2.4 结果分析

1）从两个立体像对的目视效果检查可知，不同特征地物的正射影像与参考影像的吻合度良好，几乎看不出线性地物错位。从上述检查点中误差列表中可以看出，同一立体像对1或2，后视成像（Banda）通过有理函数模型生成的正射影像平面精度优于前视成像（Bandf），这与前后视成像的侧摆角有关：前视成像侧摆角为+26°，后视成像侧摆角为-5°。

2）从表3 中可以看出，立体像对1对应的正射影像平面精度在0．5 m左右，可以理解为立体像对1对应的地物和地形主要是在城区，并没有较大的地形起伏，则传感器成像时造成影像的变形较小，因此使用优化模型的效果并不明显；而立体像对2由于地形较为复杂，影像区域为城区和地形起伏山区的混合，使用优化模型较原始模型最大误差减小了4～6 m，约2．5个像素，有效提升了正射影像的平面精度，因此通过构建优化模型生成的IRS-P5正射影像满足国家地图制图1∶25 000精度的要求。

3 结 语

高分辨率卫星影像通常使用严格轨道模型完成影像的高精度几何定位，但一方面由于卫星数据产品商对轨道和传感器参数的保密，另一方面考虑到构建严格轨道模型的复杂性，近年来，广泛使用与严格轨道模型几何定位精度相当的有理函数模型完成卫星影像的高精度几何定位。然而计算有理函数模型参数时，在行向和列向上会产生较大的系统误差，影响了影像的几何定位精度，为此，本文从影像成像时产生的系统误差着手，提出了一种有理函数优化模型，即通过定义在影像像面的仿射变换模型来减小行向和列向的系统误差以提升定位精度。研究结果表明，在地形较复杂的地区定位效果改善明显。当然，有理函数模型解算较为复杂，虚拟格网的构建和迭代算法的选择都会影响最终的参数解算精度。因此，需要进一步对其解算过程的影响因素作详细分析，从而将有理函数优化模型推广应用于国内外高分辨率卫星影像的高精度几何定位中，为卫星遥感影像产品的业务化应用提供技术支持。

[1] 陈静波,宋伟东．基于有理函数模型的IKONOS单片正射纠正方法研究[J]．测绘工程,2008,17(5):19-22

[2] 秦绪文,田淑芳,洪友堂．无需初值的RPC模型参数求解算法研究[J]．国土资源遥感,2005,17(4):7-10,15

[3] 刘军,张永生,王冬红．基于RPC模型的高分辨率卫星影像精确定位[J]．测绘学报,2006,35(1):30-34

[4] Fraser C S, Hanley H B． Bias Compensation in Rational Functions for IKONOS Satellite Imagery[J]． Photogrammetric Engineering & Remote Sensing,2003,69(1):53-57

[5] 袁修孝,汪韬阳． CBERS-02B卫星遥感影像的区域网平差[J]．遥感学报,2012,16(2):310-324

[6] 程春泉,张力． 多源航天光学影像的定位模型[M]．北京:中国测绘科学研究院,2014

[7] 张力,张继贤,陈向阳,等． 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]．测绘学报,2009,38(4):302-310

[8] Jacek G, Gene D． Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]．PE&RS,2003,69(1):59-68

[9] 张永生,刘军．高分辨率遥感卫星立体影像RPC模型定位的算法及其优化[J]．测绘工程,2004,13(1):1-4

P228

B

1672-4623（2017）01-0074-03

10.3969/j.issn.1672-4623.2017.01.023高分辨率卫星影像常使用传感器的姿轨参数和时间码构建严格轨道模型，从而实现高精度的几何定位。然而，由于卫星传感器的保密性等原因，卫星发射商往往不提供卫星轨道和传感器参数，而是使用数学意义上的有理函数模型来替代严格轨道模型完成卫星影像高精度几何定位。国内外不少学者和专家对有理函数模型有着较为深入的研究，陈静波[1]等分析推导了有理函数模型，并将其用于IKONOS高分辨率卫星影像几何定位，在平原和山区可达到5 m左右的定位精度；秦绪文[2]等详细地推导了有理函数模型的各种参数解算过程及其影响因素；刘军[3]等在有理函数模型原型公式的基础上提出了优化模型，并构建了有理函数的区域网平差模型；Fraser C S[4]等将区域网平差模型应用于IKONOS影像，取得了平面和高程均优于±1 像元的定位精度。但是，有理函数模型在解算的过程中会在影像的行和列方向上产生较大的系统误差，影响了几何定位精度；且以往的绝大多数研究成果较偏重于通过有理函数模型实现单片卫星影像的几何定位。基于上述两点，本文提出了一种基于像方坐标系的有理函数优化模型，并将其应用于IRS-P5 卫星立体像对的几何定位中以验证该方法的有效性和可靠性。

王鹏生，硕士，从事测绘科研和教学工作。

2015-12-10。

项目来源：河北省教育厅青年基金资助项目（2011134）。