基于CPSO的UAV编队集结路径规划

邵壮, 周洲, 王彦雄, 祝小平

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 航空学院,陕西 西安 710072;3.西北工业大学 无人机研究所,陕西 西安 710065)

基于CPSO的UAV编队集结路径规划

邵壮1, 周洲2, 王彦雄1, 祝小平3

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 航空学院,陕西 西安 710072;3.西北工业大学 无人机研究所,陕西 西安 710065)

针对多无人机编队集结路径规划问题,提出了具有合作机制的分布式协同粒子群(CPSO)算法。为了满足无人机运动学约束,采用曲率连续的PH曲线作为备选路径。基于协同进化思想提出CPSO算法，为每架无人机规划出一条满足机间协同约束的最优安全可飞行路径。仿真结果表明,规划得到的多条路径能够满足无人机运动学约束、安全性及无人机之间的协同性要求;相比于协同进化遗传算法,CPSO算法搜索成功率更高,稳定性更好。

无人机; 路径规划; 编队集结; PH曲线; 协同粒子群优化

0 引言

如何为多无人机(UAV)规划出能够同时到达编队集结点的安全、可飞行路径,已成为多UAV协同编队的关键技术之一[1]。多UAV编队集结路径规划是一个典型的多机协同同时到达问题。Manathara等[2]提出了基于估计到达集结点时间的一致性算法,采用的Dubins路径具有曲率不连续性,不便于跟踪实现。李杰等[3]提出了基于微分几何与李群的无人机编队会合的方法,直接以路径的曲率和挠率作为控制变量,但工程实现困难。文献[4-5]针对多架UAV同时到达多个目标问题,首先采用协同进化遗传算法为各UAV分别生成多条候选路径;然后通过求解协同函数和协同变量,来确定每架UAV同时到达各自目标点的飞行路径和飞行速度。其中Voronoi图法生成的分段直线路径需要进行后期平滑处理。

当前UAV路径规划中,采用的路径主要有Dubins路径[2]、Clothoid回旋路径、B样条曲线路径[4]和PH曲线路径[6]。本文为由不同起点出发的一组UAV分别规划出一条能够同时抵达编队集结点,并生成期望构型的安全、可飞行路径。由于PH曲线具有曲率连续、曲线平滑及曲线长度和曲率均有有理表达式的特点,因此采用PH曲线作为UAV备选路径。提出具有合作机制的分布式协同粒子群(Cooperative Particle Swarm Optimization,CPSO)算法对PH路径参数进行协同优化,使得各路径满足安全性约束、UAV运动学约束、同时达到约束及互碰避免约束,且路径的整体性能指标趋于最优。

1 问题描述与路径模型

1.1 问题描述

考虑N架UAV协同编队集结问题。假设已知第i架UAV的起点位置和航向(简称位姿)psi=(xsi,ysi,χsi)以及编队集结点处的位姿pf=(xf,yf,χf),且集结点的期望编队构型由固联于集结点的编队坐标系Ofxfyf上的一组相对位置坐标{(xfi,yfi)|i=1,…,N}定义,则该UAV的目标位姿pdi=(xdi,ydi,χdi)可由pf和期望编队构型求得。因此N架UAV协同编队集结路径规划问题描述为:

(1)

为了使各UAV同时抵达集结点时能够以相同的速度进入编队保持阶段,这里假设集结过程中各UAV均以相同的速度匀速飞行,且集结环境中仅存在少量禁飞区和障碍物;因此UAV间同时达到约束,即等价于各路径长度相等或近似相等。

1.2PH曲线路径模型

PH曲线是由Farouki等[7]提出的一种具有有理特性的参数化多项式曲线,其定义如下:

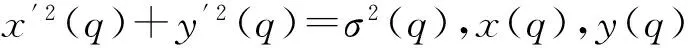
(2)

式中:pk为曲线控制顶点;n为曲线阶数。5次PH曲线是适合于无人机路径规划的最低阶PH曲线[4],因此本文采用5次PH曲线进行路径规划。

(3)

根据微分几何知识,曲线的平滑特性由曲率κ(q)描述。对于UAV,路径曲率与UAV的侧向加速度成正比,因此UAV的曲线路径需满足其自身性能决定的最大曲率约束(即UAV的运动学约束)。曲线上任一点处的曲率求解公式为[4]:

(4)

为定量描述PH曲线的平滑程度,定义曲线的弯曲能量E为曲线曲率沿曲线弧长的积分[4],即:

(5)

2 CPSO协同路径规划算法

目前,协同进化遗传算法(Cooperative Co-evolutionary Genetic Algorithms, CCGA)已经用于UAV的协同路径规划研究[8],然而CCGA算法存在搜索效率低、容易早熟收敛的缺点;因此,本文基于协同进化思想,提出了CPSO算法,实现UAV编队集结路径的协同优化。

2.1 标准粒子群算法(PSO)

设D维搜索空间中有n个粒子,第i个粒子的位置和飞行速度分别用向量Xi=(xi1,…,xiD)和Vi=(vi1,…,viD)表示。把粒子的位置带入定义的适应度函数可求得粒子对应的适应度值。设粒子i所经历过的最好位置记为粒子i的个体极值pbesti=(pi1,…,piD),整个种群所有粒子经历过的最好位置记为群体极值gbest=(g1,…,gD)。每个粒子根据如下公式进行速度和位置更新:

(6)

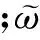
2.2CPSO算法

由前述分析可知,N架UAV协同集结路径规划问题等价于为每架UAV协同寻找一组(m0,m1),使得生成的各PH路径满足各种约束,同时所有路径的总体性能指标趋于最优或次优。将N架UAV的可行解看作N个粒子群,各子种群内的粒子按标准PSO算法独立地进行速度和位置的更新及适应度计算等操作。在进行UAV间协同评价时,各子种群分别选择代表个体进行交换形成合作团体,并对各子种群粒子进行适应度协同修正及个体极值和群体极值更新,使得各子种群分别向满足团体协同性下的最优(或次优)位置靠近。为增强搜索效率,算法采用了精英保留策略。算法流程如图1所示。

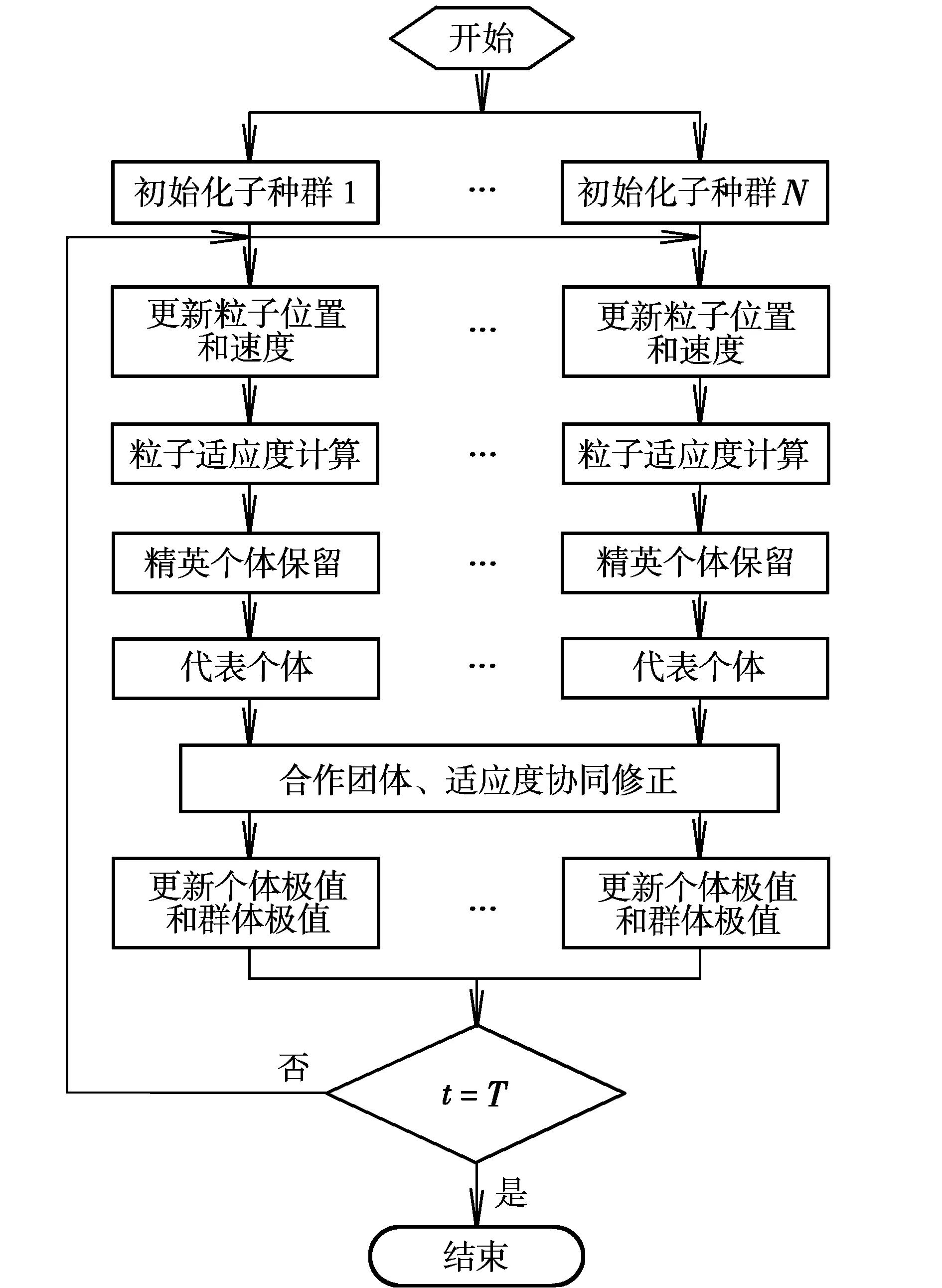
图1 CPSO算法流程Fig.1 Flow Chart of CPSO Algorithm

2.2.1 子种群初始化

由上述分析可知,任意子种群i中的粒子zij=(mij,0,mij,1)代表第i个UAV的一条候选PH路径j,其飞行速度记为Vij=(Vij,0,Vij,1),其中i=1,2,…,N；j=1,2,…,M(M为子种群规模,假设各子种群规模相同)。根据给定的取值空间[Zmin,Zmax]和[-Vmax,Vmax],随机初始化各子种群粒子的位置zij及飞行速度Vij,并采用下面介绍的适应度函数和适应度协同修正方法计算所有粒子的适应度,同时初始化各子种群的个体极值pbestij和群体极值gbesti。

2.2.2 粒子速度和位置更新

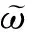
(7)

2.2.3 粒子适应度计算

为了使生成的PH路径安全可飞行,且具有较短的长度和较好的平滑性,这里定义第i个UAV(即子种群i)的适应度函数如下:

(8)

式中:w1为权值;Ji,fuel为路径燃油代价,近似等于路径长度代价;Ji,curve为路径弯曲代价,代表了路径的平滑特性,由路径弯曲能量来描述;Ji,obsc,Ji,nofly,Ji,unflyble分别为UAV避开障碍物、禁飞区以及满足UAV最大曲率约束的惩罚代价。

为便于判断,将PH路径离散为Np个点,当全部离散点均不会与障碍物发生碰撞或穿过禁飞区时,则近似认为该路径能够避开障碍物或禁飞区。此时令Ji,obsc=0或Ji,nofly=0;否则令Ji,obsc或Ji,nofly为一个很大的正数。同样地,若路径上全部离散点处的曲率均不大于UAV的最大曲率约束κmax,即认为该路径满足UAV的运动学约束,则令Ji,unflyble=0,否则为一个很大的正数。

2.2.4 粒子适应度协同修正

为实现各UAV间的空间和时间协同,各子种群完成全部个体适应度计算后,需分别提供一个代表个体(这里选取为各子种群的群体极值),并与其他子种群组成N个合作团体。生成合作团体后,需对各子种群的全部粒子进行适应度协同修正,具体方法为:对于合作团体i,判断其当前子种群i的每个个体是否会与其他子种群的代表个体发生碰撞,若会碰撞则给予一个很大的碰撞罚值,用以保证UAV间的空间协同。同时在全部N个代表个体中找出曲线长度最大的代表个体p,并令其曲线长度为参考长度Lref。若p不属于当前子种群i,则对当前子种群i的每个个体均增加一个时间协同惩罚项,用以保证各UAV的长度趋于相等。且当前个体曲线长度越接近于参考长度,罚值越小,反之罚值越大。协同修正后第i个UAV的适应度函数为:

(9)

其中:

式中:Ji,collision和Ji,dtime分别为UAV碰撞惩罚项和时间协同惩罚项;Li为某一个体的曲线长度。

下面分析UAV间不发生碰撞的条件。考虑第i和第j个UAV的PH路径ri(q)和rj(q),设UAV安全半径分别为Ri和Rj。为简单起见,将PH路径均匀离散为NPH个等分点。由于假设各UAV匀速飞行且同时到达各自目标位置,因此任意时刻下的两UAV间的最短分离距离近似等于ri(q)和rj(q)的所有相同等分点间距的最小值。PH曲线长度可由式(3)求得。因此已知PH曲线长度时,可由Newton-Raphson迭代法反解得到任一等分点处的曲线参数q,再由式(3)可得该等分点的位置坐标。假设已求得ri(q)和rj(q)的任一相同等分点k的坐标分别为(xi,k,yi,k)和(xj,k,yj,k),k=1,…,NPH,则两UAV不发生碰撞的条件可表示为:

(10)

3 仿真验证及结果分析

为验证本文算法的有效性,以3架UAV从不同基地出发集结生成V型编队的路径规划为例进行仿真试验。环境中障碍物和禁飞区分别用圆形和矩形近似,且位置和大小事先已知;各UAV的起点位姿和集结点位姿以及期望编队构型如表1所示。各UAV的安全半径均为0.1 km,最大曲率约束κmax=2 km-1,子种群规模均为M=20,最大进化代数T=50,w1=0.5,Np=NPH=50。

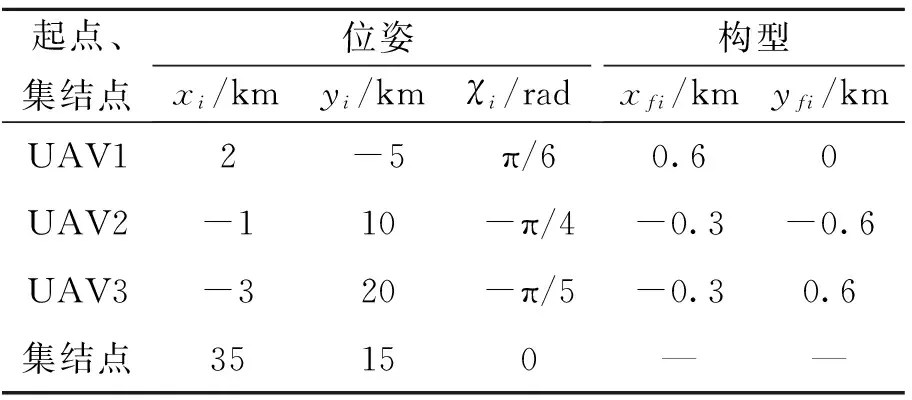
表1 UAV起点和集结点位姿及期望编队构型

仿真结果如图2和图3所示。图2为3架UAV集结路径曲线,图中■为UAV起点;●为编队集结点;▲为各UAV完成集结时的期望队形位置。图3为3条路径的曲率随路径长度的变化曲线。

图2 UAV协同编队集结路径Fig.2 Cooperative formation rendezvous paths of UAVs

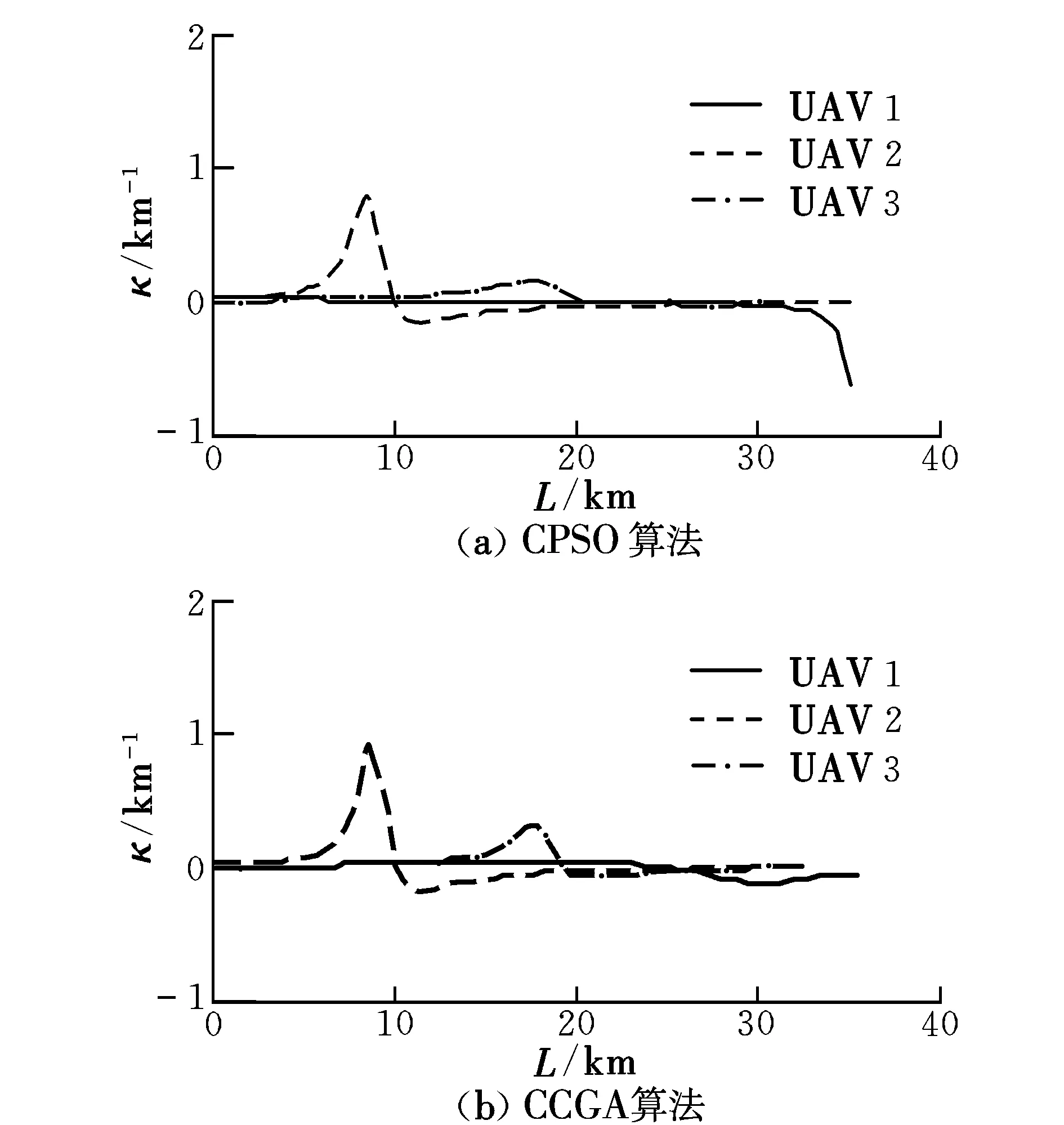
图3 路径曲率Fig.3 Path curvatures

可以看出,两种算法规划得到的3条路径均能避开障碍物和禁飞区,路径曲率连续变化且均未超过UAV的最大曲率约束,即均能满足UAV的运动学约束。表2为不同算法得到的3条路径长度及相互之间的最短分离距离。

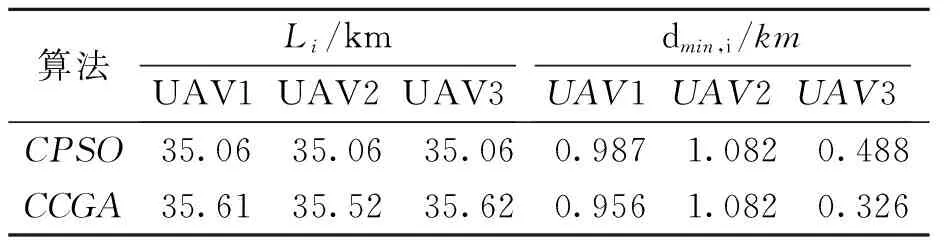
表2 路径长度和最短分离距离

由表2可知,CPSO算法得到的3条路径长度最大相差仅为2.8 m,几乎可以忽略不计。表明3架UAV以相同速度匀速飞行时能够同时到达各自目标点，形成期望编队构型,且任意两条路径间的最短分离距离均大于两架UAV的安全半径之和,即任意两架UAV均不会发生碰撞。对于CCGA算法,规划得到的3条路径长度最大相差100 m,且最大长度值偏大,说明3架UAV以相同速度匀速飞行时不能实现同时到达各自目标位置。

表3 平均长度和标准差

4 结束语

针对无人机编队集结路径规划问题,采用5次PH曲线作为UAV备选路径，并提出具有合作机制的分布式协同粒子群算法,对各UAV的PH路径参数进行协同优化,得到的各路径能够满足UAV间的协同性约束和可飞行性约束。接下来可进一步研究三维复杂环境下多UAV编队集结路径规划问题。

[1] 樊琼剑,杨忠,方挺,等.多无人机协同编队飞行控制的研究现状[J].航空学报,2009,30(4):683-691.

[2] Manathara J G,Ghose D.Rendezvous of multiple UAVs with collision avoidance using consensus[J].Journal of Aerospace Engineering,2012,25(4):480-489.

[3] 李杰,彭双春,安宏雷,等.基于微分几何与李群的无人机编队会合方法[J].国防科技大学学报,2013,35(6):157-164.

[4] 王怿.攻击型无人机协同路径规划研究[D].西安:西北工业大学,2014.

[5] 韩昕锋,叶文,陈海生,等.多UCAV协同航路规划算法[J].海军航空工程学院学报,2010,25(5):535-541.

[6] Neto A A,Macharet D G,Campos M F M.On the generation of trajectories for multiple UAVs in environments with obstacles[J].Journal of Intelligent and Robotic Systems,2010,57(1):123-141.

[7] Farouki R T,Sakkalis T.Pythagorean hodographs[J].IBM Journal of Research and Development,1990,34(5):736-752.

[8] Shorakaei H,Vahdani M,Gholami B I A.Optimal cooperative path planning of unmanned aerial vehicles by a parallel genetic algorithm[J].Robotica,2014,34(4):823-836.

[9] 史峰,王辉,郁磊,等.Matlab智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:129-136.

(编辑：李怡)

Formation rendezvous path planning for multi-UAVs based on CPSO

SHAO Zhuang1, ZHOU Zhou2, WANG Yan-xiong1, ZHU Xiao-ping3

(1.National Key Laboratory of Special and Technology on UAV, NWPU, Xi’an 710065, China;2.School of Aeronautics, NWPU, Xi’an 710072, China;3.UAV Research Institute, NWPU, Xi’an 710065, China)

To solve the problem of UAVs formation rendezvous path planning, a distributed cooperative particle swarm optimization (CPSO) algorithm was proposed. In view of the kinematic constraints of UAVs, PH curve was used because of its curvature continuity. Inspired by co-evolutionary theory, CPSO was proposed to plan a flyable safe path for each UAV, while meeting kinematic constraints of UAVs and the cooperation constraints. Simulations results show that the paths planned with CPSO could meet the kinematic constraints of UAVs, safety constraints, and the cooperation requirements between UAVs. Compared with the co-evolutionary genetic algorithms, the proposed CPSO has a higher success rate and better stability for searching.

UAV; path planning; formation rendezvous; PH curves; cooperative particle swarm optimization

2016-07-06;

2016-10-26;

时间:2016-11-10 09:12

“十二五”国防预研项目资助(41101060101)

邵壮(1987-)，男，安徽蚌埠人，博士研究生，从事多无人机编队控制、多机协同路径规划研究。

V249.1

A

1002-0853(2017)01-0061-05