模糊非基因信息记忆的双克隆选择算法

宋 丹 樊晓平 文中华 黄大足 屈喜龙



模糊非基因信息记忆的双克隆选择算法

宋 丹*①②樊晓平②③文中华①黄大足②③屈喜龙①

①(湖南工程学院计算机与通信学院 湘潭 411104)②(中南大学信息科学与工程学院 长沙 410083)③(湖南财政经济学院信息管理系 长沙 410205)

该文针对传统智能优化算法中虚拟碰撞而导致的全局搜索效率降低的问题，提出一种模糊非基因信息记忆的双克隆选择算法。该算法设计基于模糊非基因信息的搜索机制与克隆选择原理相结合，对抗体进化中的非基因信息进行采集、模糊化并保存到记忆库，运用这些信息引导该抗体后续的双克隆搜索过程，从而减少非优区域的虚拟碰撞，提高全局搜索效率。通过标准测试函数的仿真试验并与其他算法比较，新算法表现出更快的全局收敛速度和更高的全局收敛精度。

克隆选择；智能记忆；模糊信息；数值优化

1 引言

人工免疫系统是效仿人类免疫系统原理构建的一种新型计算智能系统，大多数受免疫系统启发的优化算法是基于克隆选择原理的克隆选择算法。2002年，Castro等人[1]首次构造的克隆选择算法模拟免疫应答过程并基于达尔文进化论实施进化迭代来实现寻优过程。近年来，许多学者采用设计操作算子、置入其他智能机制等方式构建新的优化算法：2010年，Gong和Jiao等人[2]将Baldwinian学习机制置入克隆选择优化算法提高了算法的寻优能力和鲁棒性；2012年，文献[3]设计混合蚁群克隆遗传算法用于全局寻优，2014年，Ho等人[4]将人口增量学习融入克隆蚁群优化算法以增强算法的启发性。2015年，Peng等人[5]设计了混合学习的克隆选择算法。此外，在许多工程应用领域，为解决高维、非线性等各类优化问题，各种新型克隆选择算法被不断设计并广泛应用于工程设计[6]、电磁设计[7]、自动聚类[8]、多目标优化[9]等优化问题。

大部分的智能优化算法是在全局解空间中采用群体采样点进行进化迭代，从而逐步寻优以实现全局优化任务。文献[10]指出虚拟碰撞在以群迭代为特征的各类智能优化算法中普遍存在，频繁的虚拟碰撞将对算法造成采样资源浪费导致算法的搜索效率降低。为了减少虚拟碰撞，各类智能优化算法经常引入记忆机制以提高算法的优化性能：如差分进化算法(differential evolutionary algorithm)[11]，超启发式进化算法(hyper-heuristic evolutionary algorithm)[12]，粒子群算法(particle swarm optimization algorithm)[13]。

依据记忆信息的存储独立性，智能优化算法采用的记忆机制可分为2种：第1种记忆机制通过进化操作本身来实现记忆，如刘若辰等人[14]提出的一种免疫记忆动态克隆策略算法、朱思峰等人[15]提出的简谐振子免疫优化算法；第2种记忆机制通过设置相对独立的数据结构进行记忆，如SPEA[16]与SPEA2[17]设置外部档案记忆非劣解以提高算法收敛速度；CW[18]算法则对选择部分不可行解性存档以利于种群通过不可行区域；邓泽林等人[19]选择邻域中距离对偶抗原最近的抗体为记忆细胞来促进抗体群体的进化。

这些智能优化算法在记忆对象上均侧重于个体或群体的基因信息，在进化迭代中保存具有优秀基因的个体或提取优秀基因片段而提高种群的整体亲和度。但是，在进化迭代中存在大量有价值的非基因信息(如探索方向、探索步长、探索结果等)，非基因信息是指进化种群的群体和个体可以从进化迭代中获取的有益于全局搜索的进化信息(不包含个体本身的基因信息)。大部分智能优化算法忽略了非基因信息的开采和利用。因此，本文在克隆选择算法的基础上提出模糊非基因信息记忆的双克隆选择算法(Double Clonal Selection Algorithm based on Fuzzy non-genetic information memory, FDCSA)，尝试对进化操作中的探索信息(非基因信息)进行相应记忆以指导后续的进化迭代过程，以期减少虚拟碰撞的发生。

2 模糊非基因信息记忆的双克隆选择算法(FDCSA)

2.1 进化迭代中的虚拟碰撞

当两个或两个以上寻优代理之间的相对距离小于由关键域所支承的“安全距离”时，即发生虚拟碰撞[10]。以进化算法在标准测试函数Rastrigin的2维解空间中的随机搜索为例，图1的3个子图均取进化代数100代的个体运动轨迹，图1(a)、图1(b)分别表示个体a和个体b在Rastrigin 2维解空间中的轨迹。图1(c)是图1(a)和图1(b)的叠加，表示个体a和b并行的进化轨迹。

从图1(a)看出，个体a多次重复搜索右下角区域，表明个体a在不同进化代数时反复搜索这一区域，即同一个体自身在多次进化迭代中也存在虚拟碰撞。图1(b)的右上部分也有类似现象出现。随后，将2个个体的运动轨迹进行叠加得到图1(c)，在问题的解空间中，2个个体之间的虚拟碰撞非常频繁。明显地，当种群规模更大时，虚拟碰撞发生的频次更高，将导致全局搜索效率降低，算法则需要付出更多的计算代价来完成全局寻优这一任务。

为了尽量减少算法中虚拟碰撞的产生，本文设计了一种模糊非基因信息记忆的双克隆选择算法。一方面，算法设计了基于模糊非基因信息的搜索机制，对进化迭代中的非基因信息(如个体在进化迭代中的搜索方向、搜索步长、搜索点的优劣信息等)进行采集、模糊化、记忆，进而引导后续进化，可以明显减少同一个体反复搜索同一区域，从而避免同一个体在不同代数时重复搜索而导致的虚拟碰撞；另一方面，算法采用较小的种群规模减少不同个体之间的虚拟碰撞，对于大部分全局优化问题，其每代的初始种群规模为3，远小于其他智能进化算法的初始种群规模。

图1 在Rastrigin函数的2维解空间中虚拟碰撞

2.2 基于模糊非基因信息记忆的双克隆选择机制

一般地，维空间的优化问题可表示为

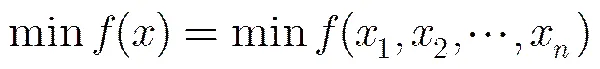
在维解空间中进行全局寻优，搜索连续实函数()的全局极小值。克隆选择算法的种群即抗体群，第个抗体是问题的一个解。由于搜索任务为全局极小值，所以，抗体x的亲和度用函数值的倒数表示。本文将问题的定义域映射到[0,1]区间，在寻优结束后再进行相应解码。

混沌初始化过程中，首先在解空间中随机生第1个随机抗体，随后依据Logistic映射生成其他抗体，产生了个抗体时，构成第1代抗体群1。在初始化过程中对记忆非基因信息的矩阵AM的所有元素设为0。

模糊非基因信息记忆的双克隆选择算法在计算亲和度后选取排名靠前的个抗体构成新一代抗体群G。通过亲和度计算后可得到抗体群G的个体排名并存入数组MR()，则第个抗体的亲和度排名为p，其双克隆次数ND按式(2)计算(设定双克隆后的抗体群规模上限为1.5)。

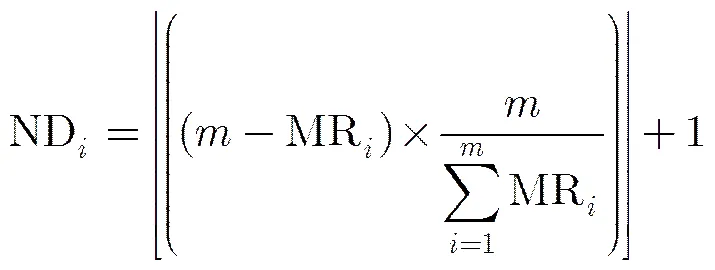
图2表示抗体G在第维上进行一次双克隆操作的具体过程，得到优胜抗体(在原抗体和2个变异抗体中择优)，如果ND大于1，则继续对抗体进行双克隆操作，如此重复进行这一操作，达到ND次为止。

抗体G随机选择其中的1维进行双克隆操作，其一次双克隆操作如图2所示。此外，对抗体G进行连续的双克隆操作时，其变异选择的维度可能不同，但由于记忆非基因信息的矩阵AM对每一维的上一次变异的非基因信息进行存储，因而能有效指导每一维的后续进化过程。这种随机性可以避免高维问题优化中维度进化不均衡的弊端。设置记忆库用以保存抗体的各个维度上一次搜索的非基因信息，上一次搜索可能发生在这一代内，也可能发生在许多代以前，通过记忆库则实现非基因信息的独立存储，有利于信息的跨代运用。

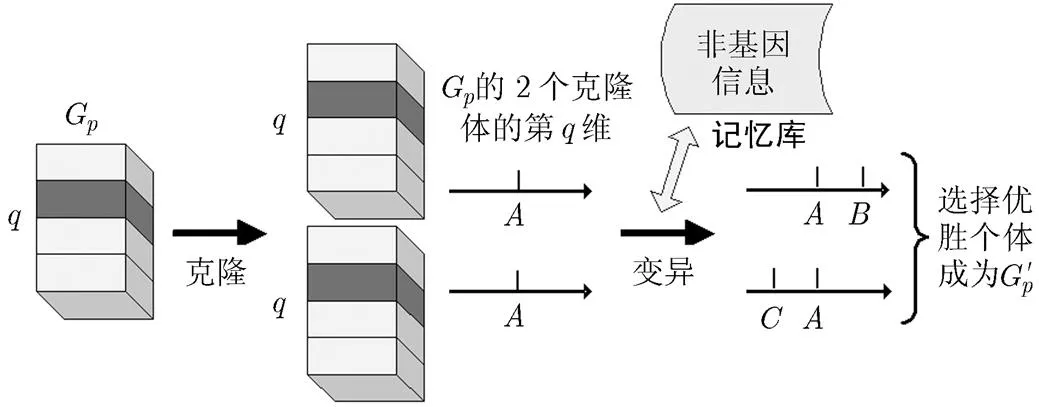
图2 FDCSA算法的单次双克隆选择操作示意图

图2中的变异采取基于模糊非基因信息记忆的变异方式进行。人类个体在成长中后天因素(非先天基因)占据主导作用，效仿人类社会的教育和后天培养机制，本文设计了非基因信息的记忆机制。从进化算法的视角出发，非基因信息是指在以群体的点迭代操作进行全局寻优的进化算法中，种群及其个体在进化中所获取的进化信息(如个体在祖辈中的搜索方向、搜索步长、搜索的目标点是否更优等信息)，不包含个体在解空间中的坐标信息(基因信息)。

图2的非基因信息记忆库通过矩阵AM(,,3)实现，AM(,,1)记录种群中第个抗体的第维的上一次搜索是否成功，如成功，标记为1，否则，标记为0; AM(,,3)记录第个抗体的第维上进行双克隆搜索的次数，为避免算法深陷局部最优的“泥潭”，设置双克隆搜索周期阈值1，当AM(,, 3)等于1时开始新一轮模糊非基因信息的双克隆搜索。

AM(,,2)记录上一次搜索尺度的模糊化信息，算法对问题的解空间映射到[0,1]区间，对[0,1]区间依据10的幂级进行细分，为区间1,为区间为区间对上一次搜索尺度对应区间标号进行记忆，以便引导下一步搜索。

基于模糊非基因信息记忆的搜索伪代码如表1所示(以抗体G为例)。

为有效使用记录的非基因信息，新算法的搜索机制采用一定概率在上次搜索尺度所属区间或相邻区间+1,-1内生成搜索尺度。以上次搜索失败为例，分配给区间,+1的概率分别为1/3, 2/3，其认为上次搜索失败时，可以给予较大的概率采用更小步长进行细微搜索来提高局部寻优精度。

基于模糊非基因信息记忆的搜索机制对父代的非基因信息进行采集、模糊化和记忆等操作，对父代的搜索尺度区间化并利用相邻区间的精度成指数级变化的特点来快速调整搜索步长，可以在一定程度上减少重复搜索，从而减少虚拟碰撞发生的概率，有利于局部搜索速度的提高；其次，双克隆的操作在相逆方向上进行探索能够避免算法在错误的单方向上进行多次的无效搜索；此外，设置适当的双克隆搜索周期阈值1，既能在周期内实现局部区域的较高精度搜索，又能在周期结束时跳出局部最优点的“陷阱”，提高全局搜索性能；在解空间中，最优抗体是当前群体中最靠近理论最优解的个体，对最优抗体的邻域进行2次的迭代搜索，有利于提高全局收敛精度。

表1 基于模糊非基因信息记忆的搜索伪代码

2.3 算法流程

通过有机结合克隆选择原理和非基因信息模糊记忆机制，本文提出一种模糊非基因信息记忆的双克隆选择算法。新算法步骤如下：

步骤1 混沌初始化第1代抗体群1，种群规模为，初始化非基因信息记忆库AM；

步骤2 判断进化代数或总评价次数是否超过设定阈值1，如是，转步骤8，否则，转步骤3；

步骤3 对抗体群进行亲和度计算并排名，选取前个抗体获得双克隆机会，亲和度排名越前，其抗体的双克隆次数越大；

步骤4 进行模糊非基因信息记忆的双克隆变异操作，其种群规模上限为3，择优留存后的群体规模为1.5；

步骤5 对最优抗体进行2次的非基因信息双克隆变异操作；

步骤6 采用小概率(0.1)对最优抗体和一个随机抗体进行单维交叉；

步骤7 综合种群的基因信息进行补充操作，补充群体规模小于0.5，补充后的群体规模为2，转步骤2；

步骤8 输出最优抗体和最优值，算法结束。

为提高群体多样性和全局搜索性能，算法的补充算子综合当前群体的所有基因信息来随机生成新个体。G表示群体中第个抗体，G表示第抗体的第维。对抗体设置影响域半径(=0.2/)，则G的影响区域为。结合该抗体的亲和度，在新抗体的第维上产生值时，采用轮盘赌的方式确定在当代群体中的某一抗体的领域内产生，在G的影响域内产生的概率如式(3)所示。

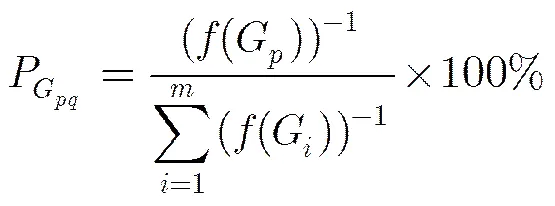
在第维上，当多个抗体的影响域出现重叠，则在重叠区域产生概率为这些抗体的之和。这种补充操作既综合考虑当代种群的基因信息，又结合所有抗体的亲和度，使之产生的新抗体具有较大概率优于普通随机方式生成的新抗体。

3 仿真试验

本文采用10个常用的Benchmark函数对模糊非基因信息记忆的双克隆选择算法进行仿真试验：Sphere, Quadric, Schwefel2.22, Schwefel2.21, Step, Rastrigin, Griewank, Schwefel2.26, Ackley, Himmelblau。函数Sphere, Quadric, Schwefel2.22, Schwefel2.21是相对简单的单峰函数，但随着维数的增高，其全局最优解变得难以获取；函数Step是一个非连续的阶跃函数；函数Rastrigin是典型的非线性的多模态函数，具有多个局部极小点，峰形呈高低起伏不定跳跃性的出现，所以很难优化查找到全局最优值；函数Griewank属于非线性的多模态函数，具有很多的局部极小点，其数量与维数相关，并具有广阔的搜索空间，被认为是很难处理的多模态优化问题；函数Ackley是指数函数叠加上适度放大的余弦而得到的起伏不平的多峰值函数，其搜索非常困难。综合来看，函数是多峰函数，在高维的情况下算法难以收敛到全局最优解；函数的全局最小值为0(均在处存在)，函数10的全局最小值为非0数值，其具体数值为-78.3323314075428数值。

表2 仿真试验中的标准测试函数

首先，对基本克隆选择算法(Clonal Selection Algorithm, CSA)和本文FDCSA算法进行对比试验，分别在30维、100维的情况下对每个函数随机独立运行30次后，统计30次运行所得最优结果的平均值(Mean)、最好值(Best)、最差值(Worst)和标准差(Standard Deviation, SD)。FDCSA算法和基本CSA算法采用的种群规模均为，算法的总评价次数(Total Number of Evaluations, TNE)取值见表3。FDCSA算法的其他参数设置如下：双克隆搜索周期阈值，最优抗体双克隆次数。

从表3的统计数据看出， FDCSA算法与CSA算法在计算代价相同(函数的总评价次数相同)的前提下，对10个标准测试函数的30、100的两个维度下进行随机试验，FDCSA算法在其中9个函数上的平均值、最好值、最差值和标准差4项指标上均优于CSA算法(除100维的4函数以外)，另一个函数5两个算法表现相当。在具体差异程度上，FDCSA算法在1,3,6-107个标准测试函数上取得较大优势。

从不同维度分析，CSA算法和FDCSA算法针对1,3,5-108个标准测试函数表现出较稳定的全局收敛性能，在100维的情况时，相应地增加总评价次数，两种算法均能维持和30维时大致相同的精度水平，其中FDCSA算法在这8个函数的100维时仍能达到1E-10以上的精度要求。对于2和4两个函数，在维度增加时，两种算法的全局寻优能力则有较明显下降。整体而言，针对大部分函数，FDCSA算法具有在超高维的情况下进行全局寻优的能力，并能达到较高精度。

为了进一步地测试FDCSA算法的性能，结合近年来的新算法PSO, GPSO, lensPSO 3种算法对函数Sphere, Quadric, Rastrigin, Griewank, Schwefel2.26, Ackley进行30次随机试验。表4中的PSO和GPSO的算法来源于文献[20]，lensPSO算法设计来源于文献[21]。3种算法的种群规模均为40，维数为30，运行最大代数为3000代。

表3 FDCSA和CSA在维度30, 100时运行30次的试验结果

FDCSA对各函数的种群规模设为3(Griewank函数设为40，由于Griewank函数具有广阔的搜索空间，并具有很多的局部极小点，对种群的多样性具有更高的要求，经过参数设置试验，确定其种群规模为40)，进化代数与对比文献相同，设为3000代，每代的函数评价次数为3.5×3+14×2+0.2= 38.7，小于对比文献的40，因此，总函数评价次数略小于对比文献(Griewank函数除外)。随机测试30次后统计结果如表4所示。针对具体函数，当一个算法在Mean, Min, Max, SD 4个指标中有3个以上的指标优于其他算法时，则在表4的Flag列标记为“E”，表示该函数上此算法表现最优。

表4表明，PSO算法与GOPSO算法在3000代内的全局收敛效果较差，而lensPSO算法与FDCSA算法的全局收敛效果明显优于其他两种算法。与lensPSO算法相比，FDCSA算法获得了5个“E”，而lensPSO算法获得了两个“E”。由于FDCSA算法针对进化迭代中的非基因信息进行了挖掘与利用，减少了重复搜索与盲目搜索，提高了搜索效率。因此，在仿真试验中，FDCSA算法表现出更快的全局收敛速度和全局收敛精度，标准差的数据则表明FDCSA算法具有更强的稳定性。

4 结束语

在人类社会中，知识学习和经验传授对个体的成长起到非常关键的作用，而这些信息均不是通过遗传基因进行传承。受此启发，本文提出模糊非基因信息记忆的双克隆选择算法。仿真结果表明，通过引入非基因信息记忆机制和双克隆搜索方式，有效减少进化迭代中的虚拟碰撞，提高全局收敛速度和全局收敛精度，在超高维的全局优化中，也具有较好的高精度搜索能力。新算法的设计和试验表明，在以群体点迭代为特征的智能优化算法中，如何更有效地减少虚拟碰撞的发生和进一步挖掘非基因信息都是值得进一步研究的问题。

表4 函数30次仿真试验的试验结果(Gmax=3000, D=30)

[1] DE CASTRO L N and VON ZUBEN F J. Learning and optimization using the clonal selection principle[J]., 2002, 6(3): 239-251. doi: 10.1109/TEVC.2002.1011539.

[2] GONG Maoguo, JIAO Licheng, and ZHANG Lining. Baldwinian learning in clonal selection algorithm for optimization[J]., 2010, 180(8): 1218-1236. doi: 10.1016/j.ins.2009.12.007.

[3] IRINA Ciornei and ELIAS Kyriakides. Hybrid ant colony-genetic algorithm (GAAPI) for global continuous optimization[J].,,, 2012, 42(1): 234-245.doi: 10.1109/TSMCB. 2011.2164245.

[4] HO S L, YANG S Y, BAI Y N,. A robust metaheuristic combining clonal colony optimization and population-based incremental learning methods[J]., 2014, 50(2): 677-680. doi: 10.1109/TMAG.2013. 2283886.

[5] PENG Y and LU B L. Hybrid learning clonal selection algorithm[J]., 2015, 296(1): 128-146. doi: 10.1016/j.ins.2014.10.056.

[6] TAYARANI-N M, YAO X, and XU M. Meta-heuristic algorithms in car engine design: A literature survey[J]., 2015, 19(5): 609-629. doi: 10.1109/tevc.2014.2355174.

[7] CAMPELO F, GUIMARÃES F G, IGARASHI H,.A clonal selection algorithm for optimization in electromagnetics[J]., 2005, 41(5): 1736-1739. doi: 10.1109/tmag.2005.846043.

[8] LIU R C, JAO L C, ZHANG X,. Gene transposon based clone selection algorithm for automatic clustering[J]., 2012, 204(22): 1-22. doi: 10.1016/ j.ins.2012.03.021.

[9] SHANG R H, JIAO L C, XU H,. Quantum immune Clone for Solving constrained multi-objective Optimization [C]. 2015 IEEE Congress on Evolutionary Compntation, Sendai, Japan,2015: 3049-3056. doi: 10.1109/CEC.2015. 7257269.

[10] 高维尚, 邵诚, 高琴. 群体智能优化中的虚拟碰撞: 雨林算法[J]. 物理学报, 2013, 62(19): 28-43. doi: 10.7498/aps.62. 190202.

GAO Weishang, SHAO Cheng, and GAO Qin. Pseudo- collision in swarm optimization algorithm and solution: Rain forest algorithm[J]., 2013, 62(19): 28-43.doi: 10.7498/aps.62.190202.

[11] MININNO E, NERI F, CUPERTINO F,. Compact differential evolution[J]., 2011, 15(1): 32-54. doi: 10.1109/tevc.2010. 2058120.

[12] SABAR N R, AYOB M, KENDALL G,. Grammatical evolution hyper-heuristic for combinatorial optimization problems[J]., 2013, 17(6): 840-861. doi: 10.1109/TEVC.2013. 2281527.

[13] BOUAZIZ S, ALIMI A M, and ABRAHAM A. PSO-based update memory for improved harmony search algorithm to the evolution of FBBFNT’ parameters[C]. 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 2014: 1951-1958. doi: 10.1109/CEC.2014.6900304.

[14] 刘若辰, 贾建, 赵梦玲, 等. 一种免疫记忆动态克隆策略算法[J]. 控制理论与应用, 2007, 24(5): 777-784.doi: 10.3969/j. issn.1000-8152.2007.05.016.

LIU Ruochen, JIA Jian, ZHAO Mengling,. An immune memory dynamic clonal strategy algorithm[J].&, 2007, 24(5): 777-784. doi: 10.3969/ j.issn.1000-8152.2007.05.016.

[15] 朱思峰, 刘芳, 柴争义, 等. 简谐振子免疫优化算法求解异构无线网络垂直切换判决问题[J]. 物理学报, 2012, 61(9): 375-384.doi: 10.7498/aps.61.096401.

ZHU Sifeng, LIU Fang, CHAI Zhengyi,. Simple harmonic oscillator immune optimization algorithm for solving vertical handoff decision problem in heterogeneous wireless network[J]., 2012, 61(9): 375-384. doi: 10.7498/aps.61.096401.

[16] ZITZLER E and THIELE L. Multi-objective evolutionary algorithms: A comparative case study and the strength Pareto approach[J]., 1999, 3(4): 257-271. doi: 10.1109/4235.797969.

[17] ZITZLER E, LAUMANNS M, and THIELE L. SPEA2: Improving the strength Pareto evolutionary algorithm[C]. Proceedings of the Evolutionary Methods for Design, Optimization and Control with Application to Industrial Problems, Athens, Greece, 2001: 19-26.

[18] CAI Zixing and WANG Yong. A multiobjective optimization based evolutionary algorithm for constrained optimization[J]., 2006, 10(6): 658-675. doi: 10.1109/TEVC.2006.872344.

[19] 邓泽林, 谭冠政, 何锫, 等. 一种基于动态识别邻域的免疫网络分类算法及其性能分析[J]. 电子与信息学报, 2015, 37(5): 1167-1172. doi: 10.11999/JEIT141077.

DENG Zelin, TAN Guanzheng, HE Pei,. A dynamic recognition neighborhood based immune network classification algorithm and its performance analysis[J].&, 2015, 37(5): 1167-1172. doi: 10.11999/JEIT141077.

[20] WANG H, WU Z and RAHANAMAYAN S. Enhancing particle swarm optimization using generalized opposition based learning[J]., 2011, 181(20): 4699-4714.doi: 10.1016/j.ins.2011.03.016.

[21] 喻飞, 李元香, 魏波, 等. 透镜成像反学习策略在粒子群算法中的应用[J]. 电子学报, 2014, 42(2): 230-235.doi: 10.3969/ j.issn.0372-2112.2014.02.004.

YU Fei, LI Yuanxiang, WEI Bo,. The application of a novel OBL based on lens imaging principle in PSO[J]., 2014, 42(2): 230-235. doi: 10.3969/j.issn. 0372-2112.2014.02.004.

Double Clonal Selection Algorithm Based on Fuzzy Non-genetic Information Memory

SONG Dan①②FAN Xiaoping②③WEN Zhonghua①HUANG Dazu②③QU Xilong①

①(,,411104,)School of Information Science and EngineeringCentral South UniversityChangshaChinaDepartment of Information ManagementHunan University of Finance and EconomicsChangshaChina

To provide a better solution for search efficiency reduction problem caused by pseudo collision in the traditional intelligent optimization algorithms, this paper proposes a double clonal selection algorithm based on fuzzy non-genetic information memory. By combing with clonal selection theory, the search mechanism based on fuzzy non-genetic information memory is well performed. The non-genetic information in antibody evolution is collected, fuzzified and stored in the memory. Using this information to guide the subsequent double cloning search process, it can reduce the pseudo collision in non-optimal area, thus the global search efficiency is improved greatly. Extensive simulations show that the proposed algorithm has fast global convergence rate and high global convergence accuracy. Comparative results further demonstrate that it performs better than existing algorithms.

Clonal selection; Intelligent memory; Fuzzy information; Numerical optimization

TP391

A

1009-5896(2017)02-0255-08

10.11999/JEIT160359

2016-04-14；改回日期：2016-09-20；

2016-11-14

宋丹 s1020d@126.com

国家自然科学基金(61272295, 61673164, 61402540)，湖南省自然科学基金(2016JJ6031, 2016JJ2040)，湖南省教育厅科学研究项目(16A049, 13A010)

The National Natural Science Foundation of China (61272295, 61673164, 61402540), The Natural Science Foundation of Hunan Province (2016JJ6031, 2016JJ2040), The Scientific Research Fund of Hunan Provincial Education Department (16A049, 13A010)

宋 丹： 男，1976 年生，副教授，研究方向为智能优化算法、多目标优化.

樊晓平： 男，1961 年生，教授，博士生导师，研究方向为智能控制、智能交通系统、无线传感器网络等.

文中华： 男，1966 年生，教授，博士生导师，研究方向为不确定性规划、物联网、图论及算法.

黄大足： 男，1968 年生，教授，研究方向为量子计算、量子通信.

屈喜龙： 男，1978 年生，教授，研究方向为云计算、智能优化算法.