实验设计及kriging响应面在优化设计中的应用*
徐兴伟,胡晓兵,武韶敏,赵清祥
(四川大学 制造科学与工程学院,成都 610065)
实验设计及kriging响应面在优化设计中的应用*
徐兴伟,胡晓兵,武韶敏,赵清祥
(四川大学 制造科学与工程学院,成都 610065)
为了减轻结构自重,需对结构进行优化设计。而复杂工程优化问题中,设计变量多且多属于非线性问题,所以对工程优化问题存在着计算时间长、优化效率低且准确性难以判断等特点。将代理模型引入在优化设计中,并通过实验设计方法得到实验设计点,根据实验设计点建立Kriging响应面,对Kriging响应面模型进行优化设计。得出该方法对结构优化设计有很显著的效果。最后以门式起重机主梁为例,建立对应的Kriging响应面进行优化设计,使用该方法优化后,其门式起重机主梁自重减轻了20%,并采用有限元方法验证了结果的准确性。对研究轻量化设计有着重要的参考及借鉴意义。
Kriging;优化设计;代理模型;实验设计
0 引言
对结构进行优化、轻量化设计等方法大量得到推广。针对这一问题,许多专家、学者提出不同优化方法对结构、工艺等参数进行优化,以获得全局最优。而代理模型是重要的优化方法,有计算量小、不降低精度等优点。常用代理模型有标准二次型、径向基函数、Kriging等模型。文献[2]提出利用二阶多项式响应面方法建立近似模型对大客车车身骨架进行优化设计。然而对于复杂工程问题往往是高度非线性问题,若采用一阶、二阶响应面方法建立近似模型只适合简单线性问题,但不适合复杂非线性的工程优化问题。文献[3]提出基于径向基函数近似模型对GOlinski's减速器进行优化设计,拟合精度较高。但对于多设计变量计算时间较长且准确性难以判断等缺点。文献[4]提出基于Kriging模型的翼型气动性能优化设计并说明Kriging代理模型的优越性。Kaymaz[5]、Sakata S[6]等人将Kriging方法进行结构优化、多学科优化以及可靠性分析中,并说明了Kriging响应面具有良好的非线性效果。根据以上论文及国内外研究情况发现,一阶、二阶等多项式响应面模型简单,计算量较小,但是对于高度非线性、多变量的工程问题很难得到解决;径向基函数近似模型具有拟合度较好,但计算时间较长且准确性难以判断等特点。所以将Kriging响应面应用在复杂工程优化问题上。该响应面模型对解决非线性的工程优化问题具有良好的效果、且具有计算效率高、时间短,响应面拟合效果好、结果准确性高等特点。为了证明该方法的有效性,以门式起重机为实例,建立Kriging响应面并对Kriging响应面进行优化设计,最后采用有限元方法验证结果的准确性。最终减轻了结构的自重,说明该方法对优化设计有着重要的重要。
1 基于代理模型优化流程
传统优化方法有周期长、精度不准、对结果验证困难等特点。基于这一问题,提出基于代理模型优化设计方法。其优化流程如图1所示。为解决复杂工程优化问题,提高效率和优化结果的准确性,该响应面模型采用Kriging响应面,实验设计方法采用最优拉丁超立方,使整个实验设计点均匀分布在空间中[7]。

图1 基于代理模型优化设计流程
1.1 优化设计模型建立
优化设计一般包括设计变量、约束条件以及目标函数。其中设计变量是在优化设计最终确定的和相互独立的设计参数;约束条件是对设计变量取值的限制条件;目标函数是以设计变量为自变量,以所要求的目标为因变量的函数。使得目标函数f(x)获得全局最优,其数学模型为:

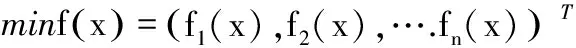
(1)
式中,f(x)、g(x)和h(x)分别为目标函数、不等式约束函数和等式约束函数;其中n设计变量个数,m、p表示对应约束函数个数。xiu、xid分别为设计变量的上限和下限。
1.2 基于Kriging(克里金)响应面模型建立
Kriging响应面是一种多维插值技术,同时考虑全局和局部的共同影响因素。而工程问题往往是复杂多变且多具有高度非线性特点。Kriging响应面通过所有设计点,因此拟合度更好,适用于高度非线性的复杂工程优化问题。既可以解决各向同性问题,也可以解决各向异性问题且可以避免一次响应面,二次响应面等拟合度较差、且可能陷入局部最优等问题。基于Kriging方法,其输出参数等于全局的设计空间加上局部偏差。其表达式:

(2)
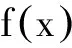
(3)
式中,σ2为方差,θ为相关函数的参数,用于衡量样本点t和样本点u之间相关性随两点间的距离增加的衰减度,相关性越小,生成的响应面越光滑。
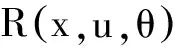
(4)

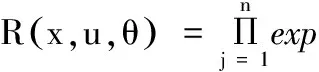
(5)
n为变异函数的维数,θ为相关函数的参数,d为数据点之间的距离。
利用实验设计的设计点形成一个相关矩阵:
(6)
其中,n为数据点总数,利用加权最小二乘法,得到Kriging模型的多项式参数:
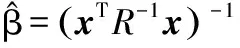
(7)
其中,x为实验设计设计点组成的系数矩阵;Y为实验设计中设计点对应的响应值。同样,方差的估计值:
(8)
最后通过实验设计的样本点和相关函数确定基函数系数β、高斯随机方差:
(9)
最终生成Kriging响应面,其任意设计点的预测值:
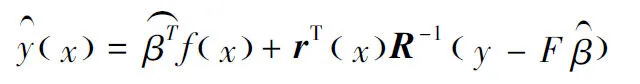
(10)
1.3 基于Kriging(克里金)响建立响应面的具体步骤
建立Kriging响应面之前,需要进行实验设计,其建立Kriging响应面流程如图2所示。建立Kriging(克里金)响应面后,并对拟合度进行检验,检查生成的响应面P值、R2及R2(adj)、s值、失拟分析、残差图。

图2 建立Kriging响应面流程图
2 算例——门式起重机主梁优化设计
2.1 门式起重机优化模型建立
门式起重机主梁属于箱形梁,由上下翼缘板和左右腹板组成。如图3,门式起重机截面图以及参数。其中X1为主梁高度、X2、X3为左右腹板,X4和X5是上下翼缘板。本文采用的模型是45t门式起重机,其中主要参数为:主梁总长度38m、跨度为L=22m、悬臂端长16m、额定起升载荷45t、小车自重35t、小车基距为5m。其设计变量的初始值以及取值区间如表1所示。其优化目标函数为结构的自重最轻,材料最省。
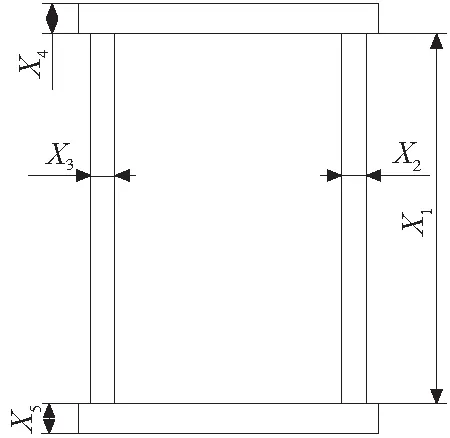
图3 门式起重机的截面以及参数
在门式起重机优化设计中,其设计变量:
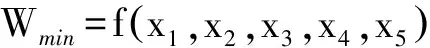

(11)


表1设计变量初始值及取值区间
2.2 实验设计
在建立Kriging响应面之前,需要进行试验设计建立样本点。实验点不同会导致建立的响应面拟合精度不同。所以选择实验设计方法对提高响应面的拟合精度有着至关重要的重要。最优拉丁超立方是对拉丁超立方抽样方法的改进,其抽样次数和拉丁超立方一致。在进行实验设计时,实验次数的选择一般取N=2n-3n(n为变量数)可得到精度要求[8]。本文采用最优拉丁超立方抽样方法,并进行27次实验设计,如表2。

表2 最优拉丁超立方实验设计
2.3 建立Kriging响应面
根据已生成的实验设计点,建立Kriging响应面。如图4设计变量对等效应力响应;图5设计变量与位移的响应;图6设计变量对结构质量响应面。并使用相对误差法进行拟合度检验,其拟合度误差都在0.95以上[9-10]。
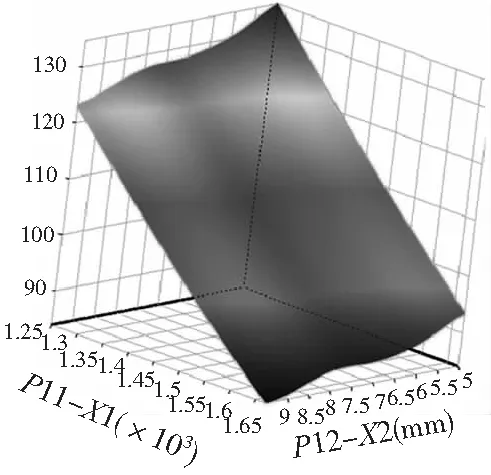
图4 设计变量对等效应力响应
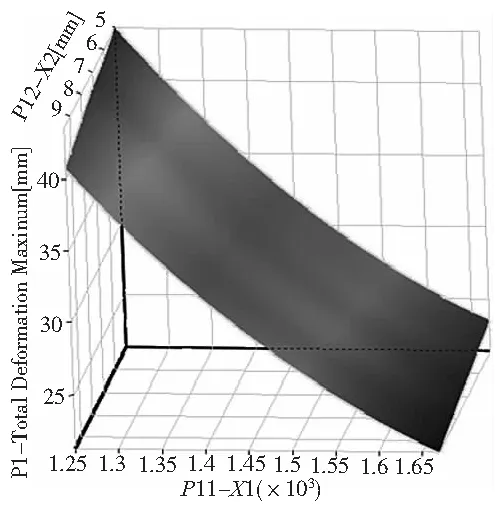
图5 设计变量对位移的响应
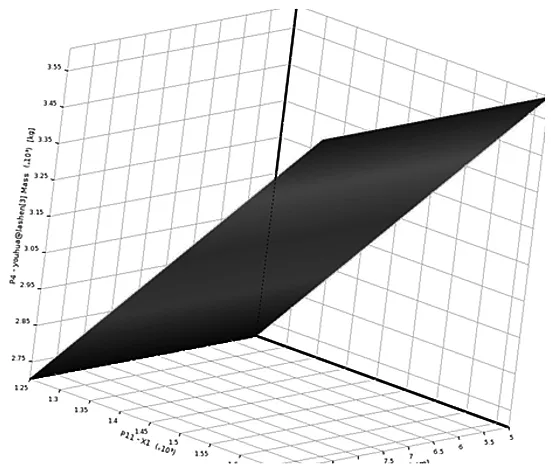
图6 设计变量对质量的响应
2.4 灵敏度分析
结构灵敏度是反映结构性能指标对某些结构参数的变化梯度,在优化设计中可以反映设计变量的结果影响情况大小的程度。通过灵敏度分析得出灵敏度曲线图,可以确定对结构响应的最敏感参数,同时对于不显著的因素进行忽略,从而减少设计变量和计算时间。如图7采用ansys软件得到门式起重机灵敏度曲线图。在灵敏度曲线图中,设计变量为正值时,表示随设计变量的增加,结构的响应值增加;设计变量为负值,表示设计变量的增加,结构的响应值减小。根据灵敏度图可知,设计变量X1、X2、X3、X4、X5越大,最大位移减少,等效应力减少,而质量增加。而对质量、等效应力、最大位移影响最大的设计变量为X1。

图7 门式起重机灵敏度曲线图
3 优化设计
通过把几何模型生成响应面模型,再用ANSYS提供的多目标遗传算法进行优化设计,迭代400次。得出5个最优的方案如表3,表4各优化方案计算结果的对比。根据表4可以得出:方案4最优。在满足约束条件作用下,方案4质量最小,自重从12503.5/kg降低到了9881/kg,质量降低了20%,而采用多项响应面的优化结果为10082.1/kg。其采用多项式响应面与Kriging响应面对比如表5所示。表5显示采用Kriging建立响应面的时间少于建立多项式响应面模型时间,且采用Kriging响应面的结果自重更轻。
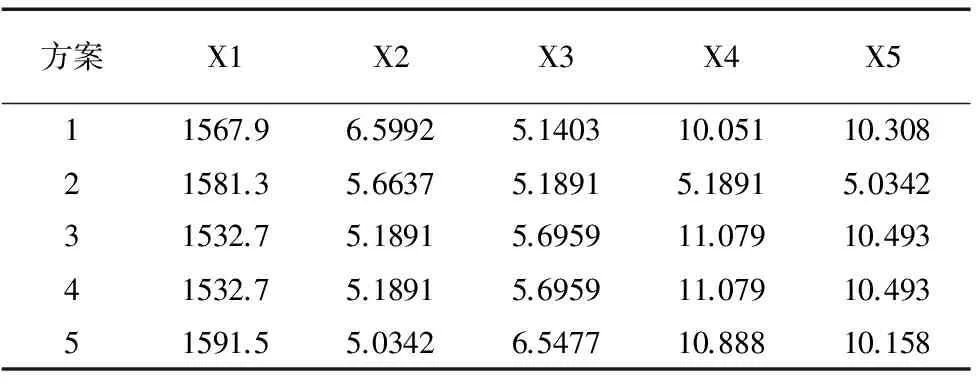
表3 优化方案
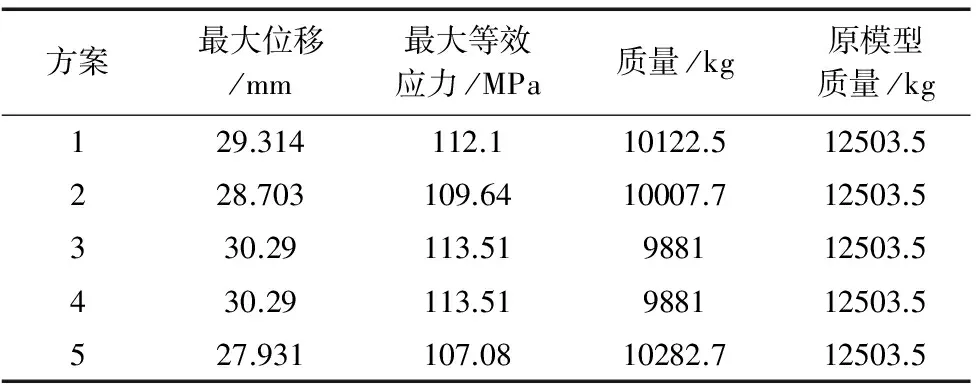
表4 方案结果对比

表5 2种近似模型优化结果
4 结果验证
建立有限元模型,把优化后的方案4参数带入有限元中进行结果验证。采用ANSYS软件建立模型并进行有限元计算,得出如图8最大等效应力图和图9最大位移云图。由云图可以得出最大的应力为112MPa,最大位移为30.404,而优化后的方案4的最大应力为113.51MPa,最大位移为30.29mm。表明了采用响应面优化与实际结果只相差1%左右。所以使用该代理模型的方法进行优化设计得出的结果是非常有效的[11-12]。

图8 等效应力云图

图9 位移云图
5 结论
(1)将代理模型引入优化设计中,建立一种基于代理模型优化设计的一般流程。通过推导出Kriging方程,采用最优拉丁超立方实验设计建立试验点,通过实验设计点和Kriging方程建立Kriging响应面。从而把优化几何模型转换为数学模型,再通过优化算法对Kriging响应面进行优化,最后得出最优结果。
(2)以门式起重机为算例,建立Kriging响应面模型。采用Kriging建立响应面,再通过ANSYS提供的多目标遗传算法对响应面进行优化设计。最终结构自重减轻了20%。
(3)引入Kriging模型在优化设计中,解决了以往优化设计中时间较长、效率较低结果准确性难以判断等确定。为复杂的工程优化问题提供参考和借鉴。
[1] 陈立周.机械优化设计方法[M].北京:冶金工业出版社,1995.
[2] 苏芮意,桂良进,吴章斌,等.大客车车身骨架多学科协同优化设计[J].机械工程学报,2010,46(18):128-133.
[3] ZHAO Min,CUI Weicheng. Application of the optimal Latin hypercube design and radial basis function network to collaborative optimizition[J].Journal of Marine Science and Application,2007,6(3):24-32.
[4] 黄章俊,王成恩. 基于Kriging模型的涡轮盘优化设计方法[J].计算机集成制造系统,2010,16(5):905-911.
[5] Kaymaz I. Application of Kriging method to structural reliability problems[J].Structural Safety,2005,27(2):133-151.
[6] Sakata S, Ashida F, Zako M. An efficient algorithm for Kriging approximation and optimization with large-scale sampling data[J].Computer Methods in Applied Mechanics and Engineering,2004,193(3):385-404.
[7] 潘峰,朱平.面向约束优化的改进响应面法在车身轻量化设计中的应用[J].机械工程学报,2011,47(10):82-87.
[8] 张勇,李光耀,钟志华.基于移动最小二乘法响应面法的整车轻量化设计及优化[J].机械工程学报,2008,44(11):192-196.
[9] Piotr B,Hakim N Alain R. Moving least squares response surface approximation: Formulation and metal forming applications[J].Computers & Structures,2006,83(17-18):1411-1428.
[10] 王亮,殷国富,谭峰,等.基于神经网络模型和网格变形技术的机床立柱优化设计研究[J].组合机床与自动化加工技术,2015(8):5-9.
[11] 熊学玉,顾炜.基于改进方法的预应力混凝土结构长期性能概率分析[J].工程力学,2010,27(4):163-168.
[12] 王礼明,田亚峰,李正羊,等.基于响应面法的数控机床工作台有限元分析与尺寸优化[J].组合机床与自动化加工技术,2015(6):28-32.
(编辑 李秀敏)
Experimental Design and Response Surface of Kriging in the Application of the Optimization Design
XU Xing-wei, HU Xiao-bing, WU Shao-min,ZHAO Qing-xiang
(School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065,China)
to reduce the weight of structure,we need to do structure optimization .but design variables are much and generally belong to nonlinear problem on complex engineering optimization problems.so there are many problems such as long computing time, low efficiency and accuracy for optimization and it is difficult to evaluate the consequences, etc. Introduce surrogate model in optimization design to establish Kriging response surface model through experimental design point and optimize Kriging response surface model.It is concluded that the method have a significant effect on structure optimization design. Finally establish Kriging response surface model for gantry crane. The weight of the structure are reduced by 25% after using Kriging response surface model in optimization design. the accuracy of the results is verified by finite element method.it has an important reference structure optimization.
Kriging; optimization; surrogate model; experimental design
1001-2265(2017)01-0062-04
10.13462/j.cnki.mmtamt.2017.01.017
2016-04-13;
2016-04-29
四川省科技计划项目(2015GZ0032,2016GZ0169)
徐兴伟(1991—),男,四川宜宾人,四川大学硕士研究生,研究方向为计算机辅助设计、机械优化设计,(E-mail)307295710@qq.com;通讯作者:胡晓兵(1970—),男,武汉人,四川大学教授,硕士研究生导师,研究方向为智能制造、CAD/CAM/CAPP,(E-mail)815183384@qq.com。
TH122;TG68
A

