含并行机器的自动化制造单元机械手调度策略*

孟现锋，罗 勇

(郑州大学 电气工程学院，郑州 450001)

含并行机器的自动化制造单元机械手调度策略*

孟现锋，罗 勇

(郑州大学 电气工程学院，郑州 450001)

文章研究了风电叶片预埋螺套智能钻孔系统(简称智能钻孔系统)的机械手调度最优策略。针对智能钻孔系统中多个并行加工机器和一个机械手难以合理调配的优化问题，提出一种将最小公倍数周期序列和遗传算法相结合的混合调度策略。论文首先分析了工件加工过程中机械手的动作特点，建立机械手搬运工件的最小公倍数周期序列模型。然后，设计遗传算法求解最优或者近似最优的最小公倍数周期序列。最后，将优化后的机械手调度策略用于实际智能钻孔生产线，并和传统的启发式算法做了对比分析，证明了该混合调度策略的有效性。

机械手；并行机器；周期序列；遗传算法

0 引言

自动化制造单元已经广泛应用于半导体制造、机械工件加工、电镀生产线等生产加工领域。这类系统通常由物料搬运机械手、输入台、输出台、机器和控制台等组成[1-3]。为了减小工件的平均加工时间，调高生产效率，越来越多的企业在加工时间较长的瓶颈工序上增加了并行机器，在同一时间同一工序上可以加工多个工件，此类系统称为含有并行机器的自动化制造单元[4]。此类制造单元的调度问题不仅要合理规划机械手的物料搬运作业，还要考虑各个并行机器的作业安排，以保证加工时间最优。

针对此类问题的优化和调度受到越来越多的学者关注。Li[5]等人提出一种混合整数规划模型求解含有并行机器的自动化制造单元调度问题。Zhang[6]等人基于最小公倍数(Least Common Multiple，LCM)周期序列算法研究了实际生产车间中机械手调度问题，并提出了优化LCM策略的算法。以上调度策略不适用于求解大规模自动化制造单元作业问题。随着自动化制造单元日趋复杂，传统的调度策略难以得到令人满意的效果，车阿大[7-9]等人设计了多种元智能算法求解自动化制造单元调度问题，取得了较为令人满意的效果，但是，对于某些工序上存在并行机器的自动化制造单元的调度问题讨论较少。

本文将LCM调度策略和遗传算法相结合，求解含有并行机器的自动化制造单元的调度问题。采用LCM策略可以避免机械手搬运作业不可行解的产生[10]。然后，设计遗传算法求解最优或者近似最优的LCM周期序列。最后，将机械手调度策略用于实际生产车间，通过真实生产数据验证调度策略的有效性。

1 问题描述及符号定义

1.1 问题描述

本文的智能钻孔生产线包括上料、卧式钻孔、立式钻孔、下料等四个环节。其中卧式加工采用2台卧式钻床(卧钻)，立式加工采用3台立式钻床(立钻)并行加工。系统模型如图1所示：机械手在中心，负责加工过程中工件的转移和上下料作业。机械手的四周，分别布置2台卧钻，3台立钻，以及码垛机。码垛机包括了毛坯料架和成品架。由于机械手可以360°旋转，并且其手臂可伸展和弯曲，具有空间的6自由度，因此可以抓取智能钻孔生产空间的任意工件，从而实现无人自动抓取作业，保证了整个生产线的全自动进行。

图1 智能钻孔生产布局图

智能钻孔系统具有以下特点：

(1)系统加工的是同一种工件，每个工件要经过两道工序，即先经过卧式机床加工，后经过立式机床加工。

(2)每个机器在同一时刻只加工一个工件，加工过程不会中断。

(3)同一工序内的并行机器具有相同的优先级。

(4)机械手同一时间一次最多搬运一个工件。

(5)各个机器之间没有工件缓存区。

Crama[11]证明该加工过程是一个周期性循环过程，即每个循环周期内加工相同数量的工件，机械手和机器恢复初始状态，与之对应会有周期性的机械手动作序列。本文的研究目标就是求解智能钻孔系统中机械手的调度问题，得到最优或者近似最优的机械手动作序列。

1.2 符号定义

M1a，M1b：卧钻工序的两台机器定义；M2a，M2b，M2c：立钻工序的3台机器定义；I：毛坯料架(输入台)定义；O：成品架(输出台)定义。

机械手的搬运作业A1γη：表示机械手将工件从第一道工序的机器M1γ下料后，移动到第二道工序，给机器M2η上料；A0*γ：表示机械手从毛坯料架取料后，给第一道工序内的机器M1γ上料；A2η*：表示机械手从第二道工序下料后，将加工完成的工件放到成品架上。其中，γ={a,b} ，η={a,b,c} ，分别对应第一道工序的两台卧钻和第二道工序的三台立钻。

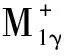
举例来说，A1ba表示机械手从机器M1b下料，随后搬运工件到机器M2a并给M2a上料；A0*a表示机械手从毛坯料架上I取下工件后，给机器M1a上料。

2 建立LCM模型

本文研究的智能钻孔系统是典型的含有并行机器的自动化生产单元，LCM策略被证明是求解此类问题的有效方法[12]，LCM策略有如下特点：

(1)一个周期内，完成加工的工件数量为λ，λ=LCM(k1,k2,…,km)。

(2)同一工序内，机器上料和下料遵守同一顺序。

(3)同一个机器上料次数和下料次数相同。

(4)同一工序内，并行机器使用的次数相同。

定义Li为第i个LCM序列，Li中的第j个子序列表示为Li,j，每个子序列完成一个工件的全部加工工序，所以LCM序列可以看作λ个单工件序列的串联。一个自动化制造单元LCM序列可以表示为：

L1=[L1,1,L1,2,…,L1,λ]
L2=[L2,1,L2,2,…,L2,λ]
…
Lξ=[Lξ,1,Lξ,2,…,Lξ,λ]

其中，i=1,2,…,ξ;j=1,2,…,λ。

本文研究的系统含有2道加工工序，k1=2,k2=3，λ=LCM(k1,k2)=6。其中一个LCM序列可以表示为：

L1=A0*aA1bcA2a*A0*bA1abA2c*A0*aA1bcA2b*
A0*bA1aaA2c*A0*aA1bbA2a*A0*bA1aaA2b*=
[A0*aA1bcA2a*,A0*bA1abA2c*,A0*aA1bcA2b*,
A0*bA1aaA2c*,A0*aA1bbA2a*,A0*bA1aaA2b*]=
[L1,1,L1,2,L1,3,L1,4,L1,5,L1,6]

该LCM序列解释如下：在循环周期开始的时候，在机器M1b和机器M2a上有工件在处理。在第一个子序列L1,1，机械手从毛坯料架拿起一个工件上料到机器M1a上，然后机械手移动到M1b，将M1b上的工件搬运到机器M2c上；随后，移动到机器M2a，把加工好的工件下料后放到成品架上，第一个子序列完成。

机械手返回到毛坯料架后，开始第二个子序列L1,2。从毛坯料架拿起工件上料到机器M1b上；机械手移动到机器M1a，从机器M1a上搬运工件上料到M2b上；然后机械手移动到机器M2c，从机器M2c上下料一个加工完成的工件放到成品架上，第二个子序列结束。其余的4个子序列的执行过程类似。

在整个LCM序列执行完成后，卧站工序内的两台机器均使用3次，立钻工序内的3台机器均被使用2次，系统的加工过程如图3所示。

图2 加工过程示意图

3 遗传算法求解LCM序列

通过以上转化，对智能钻孔系统采用类似于单工件循环的编码方式。适应度函数是LCM序列循环时间；控制策略的目标是最小化循环时间，在算法执行的过程中不断替换保存种群中适应度高的染色体，并且剔除适应度弱的染色体。实验参数选择为:种群规模为100，交叉概率为0.95，突变概率为0.1，精英概率为0.25。算法流程图如图3所示。

图3 遗传算法流程图

算法求解的机械手动作序列为：

L2=A0*aA2a*A1baA0*bA2b*A1abA0*aA2c*
A1bcA0*bA2a*A1aaA0*aA2b*A1bbA0*bA2c*A1ac

该LCM序列解释如下：在LCM序列循环开始的时候，在机器M1b,M2a,M2b,M2c上有工件正在处理，在第一个子序列内，机械手从毛坯料架上取出一个工件，上料到机器M1a；然后机械手移动到M2a，从M2a上卸下一个加工完成的工件，搬运到成品架；随后，机械手移动到M1b，将机器M1b上的工件下料后，带着工件移动到M2a，给机器M2a上料；第一个子序列执行完成。

机器人返回毛坯料架后，开始执行第二个子序列，机械手从毛坯料架把一个新的工件上料给机器M1b；然后转移到M2b，从M2b上卸载一个加工好的工件放到成品架上；随后机械手移动到M1a，给机器M1a下料，并将工件搬运到机器M2b，给机器M2b上料；第二个子序列执行完成。其余的4个子序列的执行过程类似。机械手搬运作业甘特图如图4所示。

图4 机械手搬运作业甘特图

4 实验验证

本文研究的风电叶片预埋螺套钻孔系统，以往机械手调度采用的是先请求先服务(FirstInFirstServed，FIFS)的启发式规则策略，FIFS策略可以表述为：机械手等待当前的任务完成后，按照各个机器请求时间的先后顺序执行下一步的搬运作业。在FIFS策略控制下，机械手优先响应发出请求最早的机器，不能对意外情况做出及时的响应，并且要求搬运机械手实时等待正在加工处理的工件，容易引起整个加工生产线的阻塞，影响机器的生产效率和整个生产线的加工能力。

为了改善这些不足，本文提出了LCM策略调度机械手的搬运作业，并基于遗传算法求解近似最优的LCM序列，将求解的近似最优解作为搬运机械手的控制方案。在实际加工车间中，两种控制策略实际应用的对比结果如表1所示；生产现场如图5所示。从表1看到，在实际生产线上，使用本文提出的机械手调度策略后，人力资源成本降低83.3%；产量提高50%；产品合格率提高11.2%；维护成本下降30%，很好的提高了生产企业的市场竞争力。

表1 实际加工车间生产数据

5 结论

针对智能钻孔系统加工过程中并行机器的上下料顺序和机械手调度双资源优化问题，在建立LCM周期序列模型的基础上，利用遗传算法全局寻优能力较强的特点，求解得到了最优或者近似最优的LCM周期序列，该混合算法在智能钻孔系统生产现场的实际应用表明：机械手调度采用LCM策略后，克服了传统启发式调度策略等待时间长，容易导致生产线阻塞的缺点，降低了人力资源成本和机器的维护成本，并且较大程度提高了产品产量和合格率。为含有并行机器的自动化制造单元机械手的调度提供了参考，下一步工作将研究不同工件类型以及遗传算法中变异、交叉算子等方面的机械手调度问题。

[1] 龙传泽, 杨煜俊. 基于遗传算法的柔性机器人制造单元调度问题研究[J]. 组合机床与自动化加工技术, 2015(11):141-144.

[2] FOUMANI M. Scheduling rotationally arranged robotic cells served by a multi-function robot[J]. International Journal of Production Research, 2014, 52(13):4037-4058.

[3] FOX J. Bi-objective cyclic scheduling in a robotic cell with processing time windows and non-Euclidean travel times[J]. International Journal of Production Research, 2014, 52(52):2505-2518.

[4] NADERI B, KHALILI M, KHAMSEH A A. Mathematical models and a hunting search algorithm for the no-wait flowshop scheduling with parallel machines[J]. International Journal of Production Research, 2014, 52(9):2667-2681.[5] LI Xin, CHAN F T S, CHUNG S H. Optimal multi-degree cyclic scheduling of multiple robots without overlapping in robotic flowshops with parallel machines[J]. Journal of Manufacturing Systems, 2015, 36:62-75.

[6] ZHANG J, FANG X, QI L. LCM cycle based optimal scheduling in robotic cell with parallel workstations[C]// Robotics and Automation (ICRA), 2014 IEEE International Conference on IEEE, 2014:1367-1373.

[7] 王跃岗, 车阿大. 基于混合量子进化算法的自动化制造单元调度[J]. 计算机集成制造系统, 2013, 19(9):2193-2201.[8] 李鹏, 车阿大. 基于混沌遗传算法的自动化生产单元调度方法[J]. 系统工程, 2008，26(11):75-80.

[9] YAN Pengyu, CHE Ada, CAI Xiaoqiang, et al. Two-phase branch and bound algorithm for robotic cells rescheduling considering limited disturbance[J]. Computers & Operations Research, 2014, 50(10):128-140.

[10] GEISMAR H N, DAWANDE M, SRISKANDARAJAH C. Throughput Optimization in Constant Travel-Time Dual Gripper Robotic Cells with Parallel Machines[J]. Production & Operations Management, 2006, 15(2):311-328.

[11] CRAMA Y, KATS V, KLUNDERT J V D, et al. Cyclic scheduling in robotic flowshops[J]. Annals of Operations Research, 2000, 96(14):97-124.

[12] GEISMAR H N, DAWANDE M, SRISKANDARAJAH C. Robotic Cells with Parallel Machines: Throughput Maximization in Constant Travel-Time Cells[J]. Journal of Scheduling, 2004, 7(5):375-395.

[13] 柳青红, 袁逸萍, 李晓娟,等. 基于改进遗传算法交叉算子的作业车间调度[J]. 组合机床与自动化加工技术, 2014(12):150-153.

[14] 李运霞, 杜娟, 孙王路. 基于多种群遗传算法的路径柔性车间调度问题[J]. 组合机床与自动化加工技术, 2014(3):152-155.

[15] TA Q C, BILLAUT J C, BOUQUARD J L. Matheuristic algorithms for minimizing total tardiness in the m-machine flow-shop scheduling problem[J]. Journal of Intelligent Manufacturing, 2015:1-12.

[16] LI D C, HSU P H, CHANG C C. A Genetic Algorithm-Based Approach for Single-Machine Scheduling with Learning Effect and Release Time[J]. Mathematical Problems in Engineering, 2014(1):1-12.

[17] VERMA R, PHANDEN R K, JAIN A. A Genetic Algorithm-based Approach for Job Shop Scheduling[J]. Journal of Manufacturing Technology Management, 2012, 23(7):937-946.

[18] KUMAR S. Minimizing cycle time in large robotic cells[J]. Iie Transactions, 2005, 37(37):123-136.

(编辑 李秀敏)

Scheduling Strategy for Robot in Robot Cell with Parallel Machines

MENG Xian-feng, LUO Yong

(School of Electrical Engineer, Zhengzhou University, Zhengzhou 450001, China)

The optimal scheduling strategy for robot in the intelligent drill system was studied in this paper. To solve optimization scheduling problem for intelligent drill system including parallel over several machines and a robot, a new scheduling algorithm is proposed, which combines genetic algorithms and least common multiple periodic sequence. Firstly, based on the analysis of the operating characteristics of the robot in the process, this thesis presented the least common multiple periodic sequence model. Secondly, a genetic algorithm was designed for the optimal least common multiple periodic sequence. Finally, the strategy was applied to the practical production line, in addition to comparisons with a early heuristic algorithm, and the results show that the strategy for the robot has feasibility.

robot; parallel machines; periodic sequence; genetic algorithm

1001-2265(2017)01-0042-04

10.13462/j.cnki.mmtamt.2017.01.012

2016-04-05；

2016-04-26

河南省青年骨干教师项目(2015GGJS-148)；河南省产学研合作项目(152107000058)

孟现锋(1989—)，男，安徽阜阳人，郑州大学硕士研究生，研究方向为生产计划与调度、计算机技术，(E-mail)971770764@qq.com； 通讯作者：罗勇(1989—)，男，湖南常德人，郑州大学教授，博士，研究方向为计算机控制技术,(E-mail)luoyong@zzu.edu.cn。

TH166;TG659

A