磁悬浮直线电机三维有限元分析及优化设计研究

陈永波，燕 延，王伟明，闪明才

(1.石家庄铁道大学 电气与电子工程学院，石家庄 050043；2.河北大学 质量技术监督学院，河北 保定 071002)

磁悬浮直线电机三维有限元分析及优化设计研究

陈永波1，燕 延1，王伟明1，闪明才2

(1.石家庄铁道大学 电气与电子工程学院，石家庄 050043；2.河北大学 质量技术监督学院，河北 保定 071002)

磁悬浮式运动平台易于实现大范围高精度的微运动，适合应用在精密加工和超精密测量领域。为了抑制磁悬浮直线电机电磁力谐波分量对控制系统的影响，提高磁悬浮运动平台的动态性能，以HALBACH型永磁同步直线电机为研究对象，提出了一种改进的直线电机动子HALBACH永磁阵列结构。利用有限元软件建立直线电机三维有限元模型，得到了电机水平推力和悬浮力波形，最后对电磁力波形进行了谐波分析。分析结果表明，采用优化的动子结构有效减小了直线电机电磁力波动，有利于提高磁悬浮运动平台的控制精度。

磁悬浮直线电机；HALBACH永磁阵列；三维有限元模型；谐波分析

0 引言

磁悬浮式高精度运动平台具有运动平台和驱动机构非接触、无摩擦、无磨损等优点，在现代精密加工设备、工业自动化、超精密测量等领域具有广阔的应用前景，引起了国内外学术界的广泛关注[1-3]。大行程的磁悬浮高精度运动平台主要采用直线电机作为驱动部件[4]，研究直线电机电磁力的谐波分量有利于实现高精度的磁悬浮直线电机控制系统[5]。HALBACH型永磁阵列是一种新型的永磁体排列方式，阵列经过合理设计，可以获得比常规永磁体正弦性更好的气隙磁场，并获得更高的气隙磁场基波幅值[6]。因此磁悬浮直线电机采用HALBACH阵列可以大大减小电机推力波动，提高直线电机的稳定运行性能。文献[4]分别制作了采用径向永磁阵列和HALBACH永磁阵列的直线电机样机用于对比研究，分析和实验结果表明，HALBACH型直线电机具有更高的气隙磁通密度和磁场分布正弦特性，但需要进一步优化HALBACH永磁阵列结构和尺寸。文献[7]设计了一台采用双层HALBACH永磁阵列的高速无槽永磁同步旋转电机，采用解析方法优化了弧形永磁体尺寸，气隙磁场谐波优化效果较好，但没有分析整机结构的电磁力分布情况。

目前国内外对HALBACH型永磁同步直线电机结构的研究多局限于单层HALBACH永磁阵列结构[8-9]，亟待改进HALBACH永磁阵列结构以提高气隙磁场的正弦分布特性，从而降低直线电机电磁力波动，提高电机运行的稳定性和定位精度。本文提出一种优化的双层HALBACH永磁阵列结构，不但减小了气隙磁场的谐波，而且减小了永磁阵列的质量，并对基于该结构和传统单层HALBACH阵列结构的直线电机进行了三维有限元建模及电磁力仿真对比分析，验证了其优点。

1 磁悬浮直线电机电磁力解析与结构优化设计

1.1 HALBACH型直线电机电磁力解析

图1 磁悬浮直线电机结构示意图

采用麦克斯韦应力张量(stress tensor)方法计算直线电机永磁阵列和定子绕组之间的水平推力和悬浮力[10]，在定子三相静止坐标系下，电磁力和相电流之间的关系为：

(1)

1.2 直线电机结构优化设计

传统单层四段式HALBACH永磁阵列和优化的双层阵列横截面二维拓扑结构如图2所示，永磁阵列磁化强度沿x轴周期分布，永磁体内部箭头为永磁体充磁方向，充磁方向互差900。单层HALBACH永磁阵列磁化周期为l，每块永磁体宽度和厚度T=l/4=6.6mm[11]。优化的双层HALBACH阵列结构由两组高度相同，宽度不同的永磁体上下叠加组成，两组永磁体高度均为3.3mm，其中大尺寸永磁体宽度T=6.6mm。采用步长加速法以0.66mm为间隔改变小尺寸永磁体宽度至6.6mm进行优化设计，优化的目标是保证永磁阵列产生最优正弦分布的气隙磁场并尽量减小其质量。

(a)单层HALBACH永磁阵列

(b)双层HALBACH永磁阵列图2 单层和双层HALBACH阵列拓扑结构

根据直线电机的结构形式，选择阵列下方0.25mm气隙处水平磁场波形的基波分量、高次谐波分量为设计变量，利用有限元数值分析方法仿真不同尺寸双层HALBACH阵列模型，对比分析不同模型磁场波形谐波含量如图3所示[12]。基波分量与高次谐波分量幅值比值越大，磁场波形正弦特性越好，可以看出，磁体宽度在4.8mm左右曲线达到顶点，因此确定最优化的小尺寸永磁体宽度t=4.8mm。

图3 磁场波形谐波含量随磁体宽度变化图

为使定子线圈阵列周期和上方动子永磁阵列磁场周期一致，单层HALBACH型直线电机单相绕组宽度Γ=l/6=4.4mm，双层HALBACH型直线电机单相绕组宽度为3.8mm。

2 磁悬浮直线电机电磁场有限元分析

采用三维有限元方法仿真和计算直线电机电磁场具有精度较高的特点。在有限元软件COMSOL中建立图4中所示的两种结构永磁直线电机三维有限元模型。空气框内为待研究区域，其中单层HALBACH永磁阵列由13块永磁体构成，双层HALBACH永磁阵列由26块永磁体上下叠加构成，两种电机定子线圈阵列由33块三相绕组铜线圈构成。永磁体材料采用钕铁硼，磁悬浮直线电机有限元模型参数如表1所示。

(a)单层HALBACH永磁阵列 (b)双层HALBACH永磁阵列图4 两种直线电机三维有限元模型

参数 数值(单位) 永磁体剩磁密度1．35[T]永磁体相对磁导率1．1007绕组铜线电导率5．7108e7[S/m]空气隙厚度0．25[mm]电机y轴方向长度40[mm]

对直线电机定子三相绕组施加电流iA=0.8A，iB=-1.6A，iC=0.8A，对两种电机进行有限元分析，绘制直线电机三维磁场等值线分布如图5所示。以y=40mm为坐标截取xz平面，得到平面上两种直线电机有限元模型二维磁场等值线分布如图6所示。可以看出，两种直线电机动子永磁阵列磁场具有明显的单边正弦分布特性，但阵列两端磁场存在严重畸变，即存在磁场端部效应。继续在永磁阵列下方0.25mm气隙处取三维截线，绘制直线上水平磁场强度Bx随直线位移长度变化的波形如图7所示。可以看出，电机气隙磁场分布可分划为两个区域，即端部畸变区和中间的类正弦区。端部效应的存在是造成磁悬浮永磁直线电机电磁力波动的一个主要因素[13-14]，不利于直线电机运行的稳定性。因此在保证磁悬浮直线电机长行程运动的情况下，电机动子永磁阵列周期应合理设计使磁场类正弦区足够宽以减小磁场端部效应的影响。

(a)单层HALBACH永磁阵列

(b)双层HALBACH永磁阵列图5 两种直线电机模型三维磁场分布图

(a)单层HALBACH永磁阵列

(b)双层HALBACH永磁阵列图6 两种直线电机模型二维磁场分布图

(a)单层HALBACH永磁阵列

(b)双层HALBACH永磁阵列图7 两种直线电机气隙磁场波形图

3 磁悬浮直线电机电磁力分析

3.1 直线电机电磁力有限元分析

采用洛伦兹力密度法分别分析两种不同结构直线电机电磁力，对洛伦兹力密度进行面积分得到直线电机电磁力大小。将永磁阵列在x方向上从坐标-20mm以1mm为间隔步进移动至20mm，选择所有线圈上表面为积分面，以洛伦兹力密度为积分项，分别求取每个位置上x和z方向上线圈绕组所受的洛伦兹力值，根据牛顿第三定律，得到动子永磁阵列所受水平推力和悬浮力随水平位移的变化情况，绘制的电磁力波形如图8所示。可以看出，两种结构直线电机电磁力波形呈类正弦分布，波形存在较明显的平顶波，与式(1)变化趋势相同。并且两个方向上洛伦兹力波形存在严重的非线性和耦合关系，需采用DQ解耦和局部线性化方法实现对直线电机的控制。直观上很难看出两种直线电机电磁力波形正弦性优劣，需要进一步分析两种直线电机电磁力波形的谐波特性。

(a)单层HALBACH永磁阵列

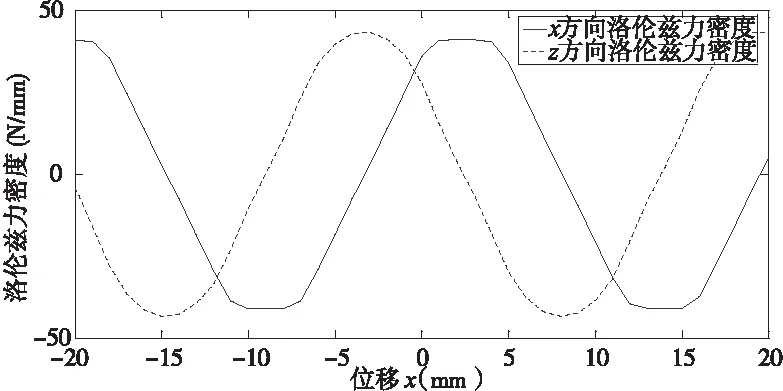
(b)双层HALBACH永磁阵列图8 两种直线电机电磁力波形图

3.2 直线电机电磁力谐波分析

为进一步分析图8中所示两种直线电机电磁力波形的谐波特性，以z方向悬浮力波形为分析对象，对电磁力波形进行谐波分析。双层永磁阵列体积约是单层永磁阵列体积的0.8637倍，对谐波幅度按质量进行归一化处理，结果如图9所示。可见在永磁阵列质量相同的条件下，单层阵列直线电机基波幅值约0.7，2次谐波幅值0.157，基波与谐波幅值比约4.475；双层阵列直线电机基波幅值约0.771，2次谐波幅值0.1645，基波与谐波比值约4.689，双层阵列直线电机电磁力基波与谐波分量比值较单层阵列直线电机提高了4.8%，并且基波幅值较单层阵列直线电机有了较大提高。

图9 两种直线电机电磁力频谱图

4 结论

以磁悬浮永磁同步直线电机为研究对象，在研究通用HALBACH型直线电机的基础上，提出一种改进的双层HALBACH永磁阵列结构。有限元仿真及对比分析结果表明，改进的双层HALBACH永磁阵列直线电机较通用单层HALBACH永磁阵列直线电机电磁力的正弦性有了较大改善，降低了电磁力波动，并且提高了直线电机力能密度，缩小了直线电机尺寸。有利于减轻对控制系统的影响和提高磁悬浮定位平台的控制品质。

[1] 王伟明, 马树元, 闪明才,等. 磁悬浮运动平台的非线性变结构控制[J]. 组合机床与自动化加工技术, 2012(3):69-72.

[2] 谢虎. 夹层结构磁悬浮纳米定位平台结构设计与控制方法研究[D]. 北京:北京理工大学, 2015.

[3] Osa M, Masuzawa T, Omori N, et al. Radial position active control of double stator axial gap self-bearing motor for pediatric VAD[J]. Mechanical Engineering Journal, 2015, 2:15-00105-15-00105.

[4] 黄学良, 张前, 周赣. 一种无铁Halbach型永磁直线电机[J]. 电工技术学报, 2010, 25(6): 1-6.

[5] 郭红, 贾正春, 詹琼华,等. 永磁同步直线电机电磁推力的谐波分量[J]. 微电机:伺服技术, 2003, 36(3):14-17.

[6] 崔皆凡, 刘娜. Halbach阵列永磁直线同步电机推力优化设计[J]. 微电机, 2012, 45(4): 8-10.

[7] 寇宝泉, 曹海川, 李伟力,等. 新型双层Halbach永磁阵列的解析分析[J]. 电工技术学报, 2015, 30(10): 68-76.

[8] 宋玉晶, 张鸣, 朱煜. Halbach永磁阵列磁场解析求解及推力建模[J]. 电工技术学报, 2014, 29(11):61-67.

[9] Chan H, Ko W, Lin K C, et al. Study of a Hybrid Magnet Array for an Electrodynamic Maglev Control[J]. Journal of Magnetics, 2013, 18(3):370-374.

[10] 王伟明, 于迟, 马树元,等. 磁悬浮运动平台电磁力有限元分析[J]. 微电机, 2011, 44(10):22-24.

[11] 仉毅, 马树元, 张磊. 磁悬浮运动平台的磁场分析及优化设计[J]. 纳米技术与精密工程, 2010,8(3): 221-225.

[12] 陈永波，王伟明，燕延，等.双层Halbach永磁阵列磁体优化设计研究[J].微特电机，2016，44(8)：29-31.

[13] 张明超, 尹文生, 朱煜. 永磁同步直线电机推力波动建模与抑制[J]. 清华大学学报(自然科学版), 2010, 50(8):1253-1257.

[14] 王昊, 张之敬, 刘成颖. 永磁直线同步电机纵向端部效应补偿方法[J]. 中国电机工程学报,2010, 30(36):46-52.

(编辑 李秀敏)

Three Dimensional Finite Element Analysis and Optimal Design of Magnetic Levitation Linear Motor

CHEN Yong-bo1， YAN Yan1，WANG Wei-ming1，SHAN Ming-cai2

(1.School of Electrical and Electronics Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China；2. School of Quality and Technical Supervision,Hebei University, Baoding Hebei 071002, China)

The magnetic suspension moving platform is easy to realize the micro motion with large scale and high precision, which is suitable for the application in the field of precision machining and ultra precision measuring. In order to inhibit the magnetic levitation linear motor electromagnetic force harmonic component influence on control system and improve the magnetic levitation motion platform dynamic performance, an improved HALBACH permanent magnet array structure of linear motor is proposed based on the research of HALBACH permanent magnet synchronous linear motor. The three dimensional finite element model of linear motor is established, and the waveform of the motor's horizontal thrust and suspension force is obtained. Finally, harmonic analysis of electromagnetic force is carried out. The analysis results show that the optimization of the motional substructure can effectively reduce the Linear motor electromagnetic force fluctuation, it is advantageous to improve the control precision of the magnetic levitation motion platform.

magnetic levitation linear motor; HALBACH permanent magnet array; three dimensional finite element model; harmonic analysis

1001-2265(2017)01-0031-04

10.13462/j.cnki.mmtamt.2017.01.009

2016-04-01；

2016-04-21

河北省自然科学基金青年基金项目(E2015210082)；河北省高等学校科学技术研究项目(QN20131084)

陈永波(1989—)，男，河南商丘人，石家庄铁道大学硕士研究生，研究方向为电力电子与电力传动，(E-mail)chenydtd@163.com；通讯作者：王伟明(1979—)，男，河北保定人，石家庄铁道大学讲师，硕士生导师，博士，研究方向为光电精密测量,(E-mail)wangwm@stdu.edu.cn。

TH166;TG659

A