基于多群体协同进化混合算法的FJSP研究*
欧阳森山,黄利福
(1.中航工业成都飞机工业(集团)有限责任公司,成都 610092;2.西北工业大学 管理学院,西安 710129)
基于多群体协同进化混合算法的FJSP研究*
欧阳森山1,黄利福2
(1.中航工业成都飞机工业(集团)有限责任公司,成都 610092;2.西北工业大学 管理学院,西安 710129)
为更有效地解决柔性作业车间调度问题,提出一种多群体协同进化混合算法,该混合算法的主群与子群分别采用带有精英保留策略的遗传算法与粒子群算法。算法初期主群与子群以不同的策略独立并行地进行寻优,后期主群与子群、子群之间按照一定的规则进行信息的交流以实现协同进化,从而提高算法前期全局搜索能力与后期局部挖掘能力。此外,借助信息熵实现了主群交叉、变异概率的自适应调整并运用凹函数递减策略对三个子群的惯性权重值进行动态调整以提高该混合算法的整体优化性能。最后,通过Kacem基准问题验证了该算法求解柔性作业车间调度问题的有效性。
柔性作业车间调度;精英保留策略;信息熵;凹函数递减策略
0 引言
进入21世纪以来,新一轮科技革命和产业变革蓄势待发,中国正在从“制造大国”向“制造强国”迈进。《中国制造2025》明确指出“以推进智能制造为主攻方向”,智能制造主要体现在“动态感知、实时分析、自主决策、精准执行”四个方面的特征,而其中“自主决策”是智能最直接体现,对于智能车间来说“自主决策”主要聚焦在柔性作业车间调度问题[1](Flexible Job-Shop Scheduling Problem,FJSP)。它是智能生产计划管理的核心,同时也是生产管理领域中最为复杂的问题之一,具有动态随机性、多约束性与多目标性等特点。
目前,柔性作业车间调度问题的有效解决方法主要集中在遗传算法[2-7]、粒子群算法[8-11]、蚁群算法[12-15]等智能优化算法。不同算法求解柔性作业车间调度问题的优化性能不同且均存在一定的缺陷,为此,众多学者对相关算法进行了一定的改进。Mitsuo Gen等[3]提出一种带有瓶颈转移的多级遗传算法。孔飞等[8]提出一种改进的双层粒子群优化算法以解决FJSP。刘志勇等[14]对蚁群算法信息素更新规则进行改进,并将其应用于解决多目标柔性作业车间调度问题。本文在前人研究的基础之上提出一种基于粒子群算法与遗传算法的多群体协同进化的混合优化算法(Multi-Swarm Cooperative Genetic Algorithm-Particle Swarm Optimization,MCGA-PSO),并以典型调度案例Kacem问题为例进行仿真模拟与对比分析以验证其可行性与有效性。
1 问题描述与模型构建
1.1 问题描述
柔性作业车间调度问题可描述为[5]:一个加工系统有n个待加工工件与m台机器,每个工件包含一道或多道工序,工件的工序的加工顺序是确定的;每道工序可在不同的机器上加工,且加工时间也不尽相同。调度的目标是合理地分配机器并确定各工序的加工顺序以使相应的性能指标得到优化。此外,在加工过程中需要满足以下约束条件[8]。
(1)同一工件的工序之间存在先后约束,不同工件的工序之间没有先后约束;
(2)一台机器同一时刻只能加工一个工件;
(3)每个工序在某一时刻只能被一台机器加工;
(4)所有工件具有相同的优先级;
(5)各工件在零时刻都可以被加工。
1.2 模型构建
基于上述柔性作业车架调度问题的描述,可以建立其相应的数学模型。模型建立过程中所涉及的符号含义如下:
n:工件数量;m:机器数量;Ji:工件集合中第i个工件;ci:工件Ji的完工时间;
vi:工件Ji包含的工序个数;pij:工件Ji的第j道工序;
sij:工序pij的开始加工时间;tijk工序pij在机器k上的加工时间;
Mij:工序pij可用的加工机器集合;mij:工序pij可用加工机器数;
Mk:机器集合Mij中的第k台机器;L:一个足够大的正数;
本文主要研究优化目标为最大完工时间的柔性作业车间调度问题,其所对应的优化模型可以表示为:
(1)
sij+xijh×tijh≤cij
(2)
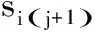
(3)
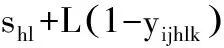
(4)

(5)
Mk⊆Mij
(6)
(7)
其中:式(1)表示优化目标为最大完工时间最小;式(2)与式(3)表示工件的各道工序之间的先后顺序约束;式(4)和式(5)表示同一时刻一台机器只能加工一个工件;式(6)表示某一工序只能由其可选机器集合中的机器加工;式(7)表示一道工序在某一时刻只能被一台机器加工。
2 多群体协同进化混合算法
2.1MCGA-PSO算法设计
在MCGA-PSO算法初期,各群体依照自身的进化规则对整个搜索空间进行独立并行的搜索以提高算法初期的全局探索能力,后期主群与子群、子群之间按照一定的规则进行信息交流,并以主群为主对搜索空间进行深度的挖掘,从而使得算法的局部挖掘能力及收敛精度得到提高。此外,为了避免单一遗传算法、粒子群算法易早熟收敛的缺陷,提高种群的多样性,MCGA-PSO算法主群借助种群信息熵均值实现交叉概率与变异概率的自适应调节,同时将凹函数递减策略引入到3个子群中以实现惯性权重值的动态调整,并运用精英策略保留进化过程中的优势个体。MCGA-PSO算法的具体操作步骤如下所示:
步骤1:初始化主群与子群相关参数。
步骤2:分别计算主群与3个子群个体的适应度值,并记录进化过程中产生的最优个体。
步骤3:gen=gen+1,对主群中的个体进行交叉与变异操作并更新子群粒子的位置与速度。
步骤4:判断gen是否小于iter,若小于则返回步骤2。否则,执行步骤5。
步骤5:计算主群与3个子群个体的适应度值,并分别筛选出3个子群中的最优粒子,并将其转换之后替换主群中适应度较差的个体。
步骤6:gen=gen+1,主群中的个体进行交叉与变异操作并更新子群粒子的位置与速度。
步骤7:判断gen是否小于maxgen,若小于则转至步骤5。否则,输出最优解。
MCGA-PSO算法流程如图1所示。

图1 MCGA-PSO算法流程
2.2MCGA-PSO算法参数设计
(1)交叉概率与变异概率设计
遗传算法中的交叉算子与变异算子对算法的收敛性具有关键性的影响,而在传统遗传算法搜索过程中它们的值是固定不变的,致使算法易陷入局部最优解。因此,本文将信息熵融入MCGA-PSO算法中来衡量种群中个体的差异程度,并借助信息熵实现算法中的交叉概率Pc及变异概率Pm值的动态自适应调整。
假设种群具有M个个体,每个个体由N个基因组成,设Rj是M个个体第j位基因值的集合,bij表示第i个个体第j位基因值在Rj中的重复数,Pij表示第i个个体第j位基因值在Rj中的所占比例。种群第j位基因的信息熵可通过下式计算得出[11]:
(8)
种群的多样性可用种群所有基因位的平均信息熵H来衡量:
(9)
主群的自适应交叉概率Pc与自适应变异概率Pm分别为:
(10)
(11)
其中,Pc1与Pc2分别为最大与最小交叉概率,Pm1与Pm2分别为最大与最小变异概率。
(2)惯性权重设计
粒子群算法中的粒子通过不断追寻个体极值及群体极值进行全局最优搜索。搜索过程中,各粒子依据群体极值与个体极值粒子的位置不断更新自身的速度及位置,其速度与位置的更新公式如下:

(12)
(13)

惯性权重ω表明粒子当前速度受历史速度的影响程度,它可以有效的平衡算法的全局探索能力与局部挖掘能力,提高算法的优化性能。在本文所提的MCGA-PSO算法中,3个子群的惯性权重值采用凹函数递减的策略进行调节,以使算法的优化性能得到提高。

(14)
公式(14)中,t为当前进化代数;tmax为最大的进化代数;ωmax与ωmin分别代表ω的最大值与最小值。
2.3 编码
由于FJSP不仅需要确定工序的加工顺序,还要解决各工序的机器分配问题,基于工序的编码方式已不能满足其需要,本文采用分段式的编码方式,该编码包括工序的排序机器的选择两部分。
工序排序部分:每一基因代表一个工序,同一工件的工序用相应的工件号表示,并且同一工件序号出现的次数与该工件的工序总数相等,其出现的第k次表示该工件的第k道工序。
机器选择部分:机器选择部分的基因对应的数字表示该工序的可选加工机器集合中相应的机器序号。
图2为一个编码案例,前半部分表示工序的排序,后半部分为机器的选择。

图2 分段式编码方式
如工序排序部分的第一个数字为2,且数字2第一次出现,则它表示工件J2的第1道工序,第4基因位上的数字2表示工件J2的第2道工序,以此类推。在机器选择部分,如工序O11的可选加工机器集中有三台机器,则该基因位对应的数字3表示可选机器集合中的第3台机器,即机器M3。
2.4 位置与速度的更新
工序排序部分的迭代更新:由于粒子群算法对应的是连续空间而柔性作业车间调度则属于离散空间优化问题,所以在实现速度与位置的更新之后需要对其进行适当的调整以满足问题的需要。具体操作如图3所示。

图3 工序排序部分更新
机器选择部分的迭代更新:在工序排序部分完成更新之后,机器选择部分各位置根据其所对应的工序进行更新,其数值为介于[1,m]之间的随机整数值,m代表该工序可选机器数。
2.5 遗传算法操作
(1)选择操作
选择操作是MCGA-PSO算法中的一个关键操作,本文采用根据个体适应度值对种群中的个体进行优胜劣汰的轮盘赌选择策略,其选择概率公式如公式(15)所示:

(15)
其中:P(xi)为个体xi的选择概率,f(xi)为个体xi的适应度值。
(2)交叉操作
本文采用张超勇等[7]所提出的POX交叉方式实现工序排序部分的交叉,机器选择部分采用多点的交叉方式。
工序POX交叉方式步骤如下:
1)随机划分工件集{1,2,…,m}为两个非空子集J1和J2;
2)将Parent1与Parent2中包含在J1集合中的工件号分别复制到Children1与Children2;
3)将Parent2中包含在J2的工件号依次复制到Children1,将Parent1中包含在J2的工件号依次复制到Children2。
POX交叉方式具体操作过程如图4所示。

图4 POX交叉
机器多点交叉方式如图5所示,首先随机产生一个由0、1组成且长度为工序总数的rand0&1集合,而后互换两个父代0位置的基因,1位置的基因保持不变。

图5 多点交叉方式
(3)变异操作
遗传算法解决柔性作业车间调度问题时常使用的变异算子有插入变异、逆转变异和交换变异等。针对柔性作业车间调度问题的特点,本文采用两种不同的变异操作分别实现工序排序与机器选择两部分的变异。工序排序部分采用交换变异的方法,即随机选择两个工件的工序(基因)而后调换这两个基因,各工序所选择的机器不变。机器选择部分采取两点变异的方法,首先随机选取机器选择部分的两个基因,而后在各基因所对应工序的可选机器集合中随机选择一台机器替换原机器。
3 实例仿真与结果分析
为验证MCGA-PSO算法求解FJSP问题的有效性,本文选取典型调度案例Kacem基准问题[16]中的8×8部分柔性调度问题与10×10的全部柔性调度问题进行测试。通过Matlab7.0编程实现MCGA-PSO算法的具体应用,MCGA-PSO算法的主要参数设置如下:主群数P=1,子群数Q=3,各种群个体数psize=100,iter=400,maxgen=600,Pc1=0.8,Pc2=0.1,Pm1=0.3,Pm2=0.1,ωmax=0.9,ωmin=0.1,c1=c2=1.5,每个实例独立运行10次。
表1给出了MCGA-SPO算法求解Kacem基准问题的结果,同时与其它算法的运行结果进行对比以验证该算法的性能。MCGA-PSO算法求解Kacem问题的收敛曲线与最优解甘特图如图6~图9所示。

表1 Kacem基准问题测试结果比较
由表1可以看出MCGA-PSO算法求解Kacem基准问题所得的最优解均已达到参考文献中的最优值,且从其收敛曲线图可以看出该算法在求解柔性作业车间调度问题时具有较好的收敛精度与收敛速度,验证了该算法的有效性。

图6 8×8 Kacem问题

图7 10×10 Kacem问题
4 结论
针对柔性作业车间调度问题的特点,本文在粒子群算法与遗传算法的基础上,提出一种多群体混合优化算法,并对算法相关参数进行了详细设计。该混合算法分为独立并行进化与协同进化两个阶段,大幅增强了算法的全局搜索能力与局部挖掘能力,能够有效地避免单一粒子群算法与遗传算法易陷入早熟收敛的缺陷。最后,基于Kacem实例的仿真实验表明该算法能够有效地应用于解决柔性作业车间调度问题。
[1] 石小秋,石宇强,袁雪娇. 离散多种群入侵杂草优化算法求解柔性作业车间调度问题[J]. 信息与控制,2015,44(2):238-243.
[2] 刘琼,张超勇,饶运清,等. 改进遗传算法解决柔性作业车间调度问题[J]. 工业工程与管理,2009,14(2):59-66.
[3] Gen M, Jie G, Lin L. Multistage-Based Genetic Algorithm for Flexible Job-Shop Scheduling Problem[J]. Studies in Computational Intelligence, 2009:183-196.
[4] Giovanni L D, Pezzella F. An Improved Genetic Algorithm for the Distributed and Flexible Job-shop Scheduling problem[J]. European Journal of Operational Research, 2010, 200(2):395-408.
[5] 张超勇,饶运清,李培根,等. 柔性作业车间调度问题的两级遗传算法[J]. 机械工程学报,2007,43(4):119-124.[6] ZHANG Guohui. Improved Genetic Algorithm for the Flexible Job-shop Scheduling Problem[J]. Journal of Mechanical Engineering, 2009, 45(7):145-151.
[7] 张超勇,饶运清,刘向军,等. 基于POX交叉的遗传算法求解Job-Shop调度问题[J]. 中国机械工程,2004,15(23):2149-2153.
[8] 孔飞,吴定会,纪志成. 基于双层粒子群优化算法的柔性作业车间调度优化[J]. 计算机应用,2015,35(2):476-480.
[9] Lim W H, Isa N A M. An adaptive two-layer particle swarm optimization with elitist learning strategy[J]. Information Sciences, 2014, 273: 49-72.
[10] 宋存利. 求解柔性作业调度问题的协同进化粒子群算法[J]. 计算机工程与应用,2013,49(21):15-18.
[11] 黄英杰,姚锡凡,古耀达. 基于熵的混合粒子群算法在柔性调度中的应用[J]. 湖南大学学报(自然科学版),2012,39(3):48-52.
[12] Huang R H, Yang C L, Cheng W C. Flexible job shop scheduling with due window—a two-pheromone ant colony approach[J]. International Journal of Production Economics, 2013, 141(2): 685-697.
[13] Rossi A, Dini G. Flexible job-shop scheduling with routing flexibility and separable setup times using ant colony optimisation method[J]. Robotics and Computer-Integrated Manufacturing, 2007, 23(5): 503-516.
[14] 刘志勇,吕文阁,谢庆华,等. 应用改进蚁群算法求解柔性作业车间调度问题[J]. 工业工程与管理,2010,15(3):115-119.
[15] 薛宏全,魏生民,张鹏,等. 基于多种群蚁群算法的柔性作业车间调度研究[J]. 计算机工程与应用,2013,49(24):243-248,261.
[16] Kacem I, Hammadi S, Borne P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems [J].IEEE Transactions on systems,Man and Cybernetics:Part C,2002,32(1):1-13.
[17] 董蓉,何卫平. 求解FJSP的混合遗传—蚁群算法[J]. 计算机集成制造系统,2012,18(11):2492-2501.
(编辑 李秀敏)
Flexible Job-shop Scheduling Study Based On Multi-swarm Cooperative Hybrid Algorithm
OUYANG Sen-shan1,HUANG Li-fu2
(1.Chengdu Aircraft Industrial (Group) Co., Ltd, Chengdu 610092,China;2. School of Management, Northwestern Polytechnical University,Xi’an 710129, China)
In order to solve flexible job-shop scheduling problem more efficiently, a new multi-swarm cooperative hybrid algorithm is proposed in this paper, genetic algorithm with elite strategy and particle swarm algorithm were utilized in the master swarm and slave swarms respectively. In order to improve the global search ability of the proposed algorithm, parallel optimization calculation was performed in the master swarm and the slave swarms at the early stage. At the later stage of the algorithm, the master swarm and slave swarms share information according to certain rules to enhance the local search ability and optimization accuracy of the proposed algorithm. Besides, in order to improve the overall optimization performance of this hybrid algorithm, crossover probability and mutation probability were adjusted adaptively according to population information entropy and concave function decreasing strategy was adopted in the inertia factor. Finally simulation results on benchmark Kacem instance demonstrate the effectiveness of the proposed algorithm.
flexible job-shop scheduling problem; elitist strategy ;information entropy; concave function decreasing strategy
1001-2265(2017)01-0023-05
10.13462/j.cnki.mmtamt.2017.01.007
2016-04-13;
2016-04-27
国家自然科学基金项目(U1404702)
欧阳森山(1982—),男,四川彭州人,中航工业成都飞机工业(集团)有限责任公司工程师,硕士,研究方向为车间调度优化,(E-mail)1465527151@qq.com;通讯作者:黄利福(1991—),男,河南兰考人,西北工业大学硕士研究生,研究方向为车间调度优化,(E-mail)1036205547@qq.com。
TH166;TG506
A

