汽车制动踏板特性仿真及踏板感觉优化
裴晓飞,董兴智,张灿明,潘 浩,张 杰
(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学 汽车零部件技术湖北省协同创新中心,武汉 430070;3.万向集团 技术中心,杭州 311215)
汽车制动踏板特性仿真及踏板感觉优化
裴晓飞1,董兴智1,张灿明2,潘 浩2,张 杰3
(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学 汽车零部件技术湖北省协同创新中心,武汉 430070;3.万向集团 技术中心,杭州 311215)
围绕汽车的制动踏板特性展开研究,揭示了制动减速度、制动管路压力、踏板位移以及踏板力之间的变化关系。建立面向制动踏板感觉的制动系统各元件的动力学模型,并在AMESim软件中建立相应的静态/动态仿真模型,结合实车试验验证了仿真模型。基于模型研究了橡胶反作用盘刚度以及制动软管变形对踏板特性的影响。采用制动踏板感觉指数(Brake Feeling Index,BFI)评价体系对试验样车的制动踏板进行客观评价,并提出了优化方案。优化结果表明,通过减小制动盘与制动块之间的间隙,提高制动软管杨氏模量以及橡胶反作用盘刚度等措施,能够显著改善现有的制动踏板感觉,从而为设计出具有良好踏板感觉的制动系统奠定理论基础。
车辆工程;制动踏板;建模仿真;踏板感觉优化
汽车制动性能是汽车的重要性能之一,用户对制动性能的主观评价也越来越重视[1],尤其是制动踏板感觉。踏板感觉通常以踏板行程、踏板力和制动减速度三者之间的关系来描述[1]。例如制动“软”和“不灵”对应着小的踏板力、长的踏板行程,以及较弱的减速能力,其优势在于中低速行驶时,制动力更容易把控,劣势在于紧急制动时需要更大的制动力和更长的踏板行程。制动“硬”和“灵”则恰好相反。
为便于研究驾驶员踩下制动踏板时的感觉,1994年,通用公司的EBERT 等[2]提出BFI的概念,首次将主观评价指标转化为客观测量指标。泛亚技术中心也基于BFI 对各类车型进行了测试,并分析了试验结果[3]。菲亚特公司的PASCAL等[4]通过以用户为导向对制动系统的研究,提出了一套新的制动感觉评估方法,主要研究制动效率、制动操控性、踏板反应能力、踏板力、踏板位移和踏板响应能力。制动质量感觉指数研究(Index of Brake Quality Feeling,IQF)和BFI 研究非常相似,IQF的研究在BFI 的基础上增加了一些参数,但最基本的参数包括踏板力、踏板位移和踏板响应能力这些关键参数却没有变化。中国汽车技术研究中心的梁荣亮等[5]以Matlab 软件为开发平台,搭建了一套获取制动系统参数的数据采集系统,并利用该数据采集系统对某款SUV 进行静态和动态制动试验,为后续该车型底盘制动系统的匹配及试验提供参考指导。同济大学的孟建德等[6]为了弥补制动踏板感觉整车试验和评价的不足,研究关键因素对制动踏板感觉的影响,开发了乘用车制动踏板感觉试验台架,并制定了台架评价方法。
在制动过程中,驾驶员和车辆构成一个闭环反馈系统[7]。制动踏板将踏板力和踏板位移反馈给驾驶员,车辆则将制动减速度反馈给驾驶员,以便驾驶员采取进一步的制动操作。而随着电子液压制动系统(Electronics Hydraulic Brake,EHB)的发展,踏板模拟器作为其中的关键部件,需要更真实地模拟传统制动踏板特性[8-9]。因为驾驶员在长期的制动操作中,已被训练成更适应这种带有真空助力形式的制动踏板感觉。本研究首先建立了面向踏板感觉的制动系统动力学模型,然后对建立的仿真模型进行了静态与动态试验验证。基于模型讨论了与制动踏板特性相关的影响因素,最后结合BFI评价体系提出了优化踏板感觉的可行措施。
1 动力学建模
1.1 制动踏板模型
为了建立制动踏板的动力学模型,作如下假设:不考虑制动踏板惯量对制动系统的影响,并将其简化为静力学杠杆模型。由于踏板回位弹簧和杠杆比对踏板力和踏板位移影响很大,所以在建立制动踏板运动学和静力学模型时,必须要考虑这些参数的作用。
踏板运动学主要分析踏板位移与推杆位移以及回位弹簧压缩量之间的变化关系。
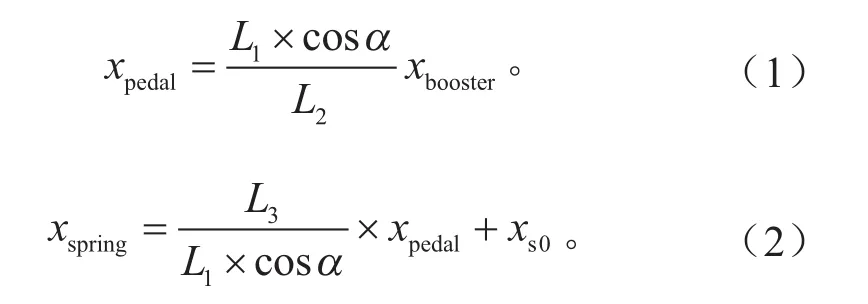
式中:xpedal为制动踏板位移,mm;xbooster为真空助力器推杆位移,mm;xspring为制动踏板回位弹簧压缩量,mm;L1为踏板输入力到踏板支点的距离,mm;L2为真空助力器推杆到支点的距离,mm;L3为制动踏板回位弹簧到支点的距离,mm; 为制动踏板初始位置时踏板在y方向上的投影与竖直方向之间的夹角,rad;xs0为制动踏板回位弹簧预压缩量,mm。
踏板静力学主要分析真空助力器推力与踏板力和踏板回位弹簧力之间的关系。
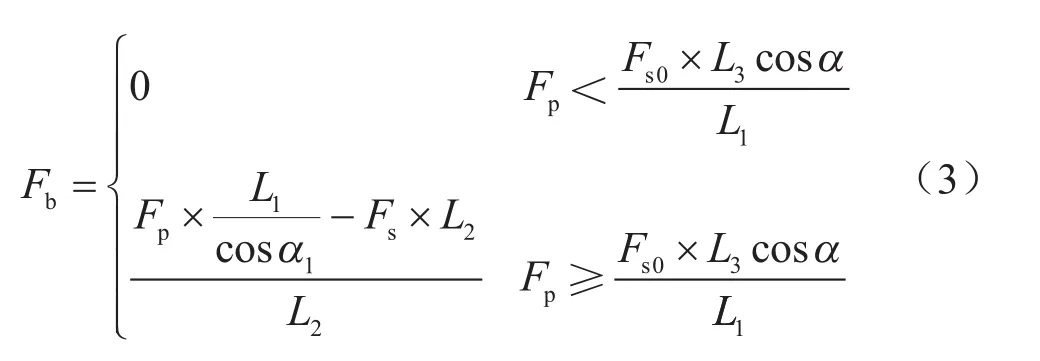
式中:Fp为踏板力,N;Fb为真空助力器推杆对踏板的作用力,N;Fs0为制动踏板回位弹簧预紧力,N,Fs0= ks× xs0;Fs为制动踏板回位弹簧力,N,Fs= ks× xspring;ks为制动踏板回位弹簧刚度,N/mm;α1为踏板转角,rad。
1.2 真空助力器模型
真空助力器位于制动踏板与制动主缸之间,利用发动机进气歧管真空度来放大踏板力。而橡胶反作用盘作为真空助力器中的核心部件,决定着真空助力器的助力比。由于橡胶元件具有同液体一样传递压力的性质[10],所以可以将其简化为一个液压缸,如图1所示。该液压缸带有两个活塞,分别为圆柱形主面和圆环形副面,横截面积分别为As1和As2。
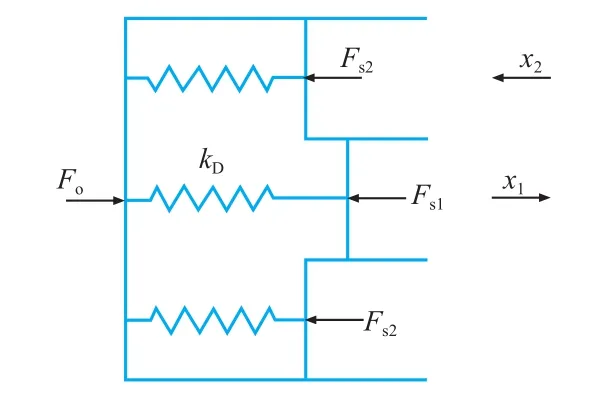
图1 橡胶反作用盘简化模型
根据质量守恒定律及力的平衡方程,联立上述方程解得:
式中:As1为圆柱形主面面积,mm2;As2为圆环形副面面积,mm2;x1为圆柱形主面变形量,mm;Fs1为柱塞阀作用于橡胶反作用盘的力,N;Fs2为真空助力器伺服助力,N;kD为橡胶反作用盘刚度,N/mm;Fo为橡胶反作用输出力,N。x2为圆环形副面变形量,mm;p为橡胶反作用盘内压强,MPa。
1.3 制动主缸模型
制动主缸是将推杆力转换为系统液压力的起始部件。为了建立主缸动力学模型做基本假设如下:忽略制动主缸前腔和后腔的制动液流动造成的压力损失,认为同一腔内压力处处相等;制动液在工作过程中,温度保持不变;制动活塞皮腕与主缸壁之间的摩擦力恒定。
制动主缸的运动可分为3个阶段:
第1阶段,随着输入力FBo逐渐增大,由于第2活塞回位弹簧预紧力大于第1活塞回位弹簧预紧力,当输入力大于第1活塞回位弹簧预紧力时,第1活塞回位弹簧开始压缩,第2活塞静止不动,直到输入力FBo增大到等于第2活塞回位弹簧预紧力。
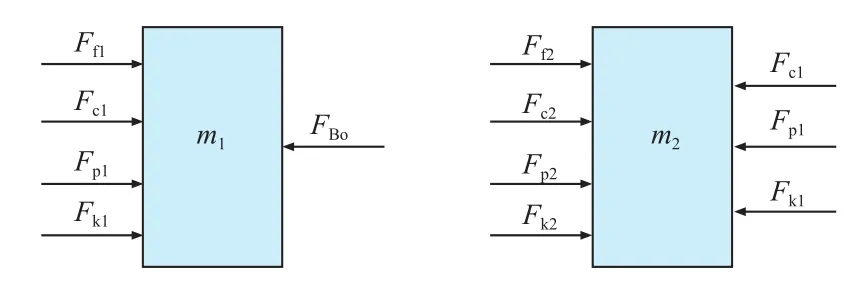
图2 第1/第2活塞受力分析图
第2阶段,当输入力FBo增大到大于第2活塞回位弹簧预紧力时,第2活塞回位弹簧开始压缩,此时,第1活塞和第2活塞以不同的速度一起运动。
第1活塞和第2活塞的受力分析示意图如图2所示,于是有:
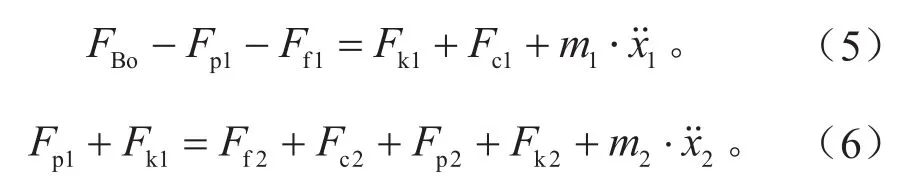
式中:Fp1、Fp2分别为第1、第2活塞腔油压对活塞的作用力,分别为主缸缸壁对第1、第2活塞的摩擦力,N;k1、k2分别为第1、第2活塞回位弹簧刚度,N/mm;c1、c2分别为第1、第2活塞阻尼系数;x1、x2分别为第1、第2活塞位移,mm;Am为主缸活塞面积,mm2;Fk1、Fk2分别为第1、第2活塞回位弹簧作用力,N,分别为第1、第2活塞回位弹簧预压缩量,mm;Fc1、Fc2分别为第1、第2活塞阻尼力,N/(mm·s-1),
第3阶段,当第2活塞回位弹簧压缩到极限位置时,只有第1活塞继续运动。
该阶段第1活塞受力同第1阶段,其动力学方程为:
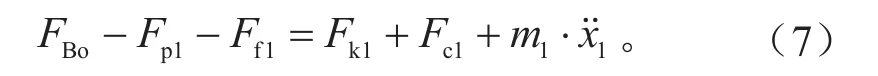
在主缸实际工作时,FBo并不是从0开始逐渐增大的,真空助力器输入输出特性上存在一个阶跃值。该阶跃值远大于第1活塞回位弹簧和第2活塞回位弹簧预紧力之和,故主缸工作时没有上述第1阶段,只有第2阶段和第3阶段。
1.4 制动液模型
根据流体的连续性原理,对主缸第1活塞腔有:
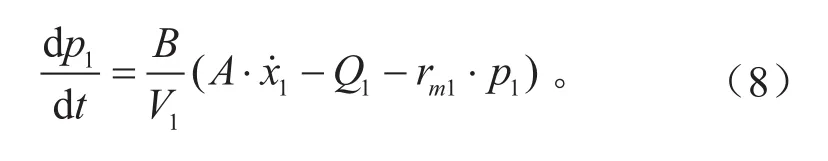
对主缸第2活塞腔有:
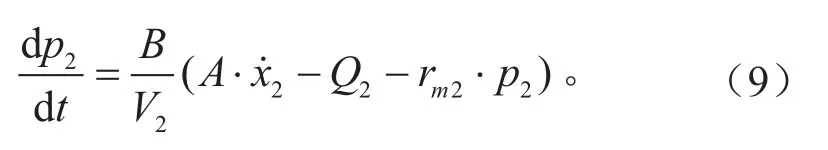
式中:p1、p2分别为第1、第2活塞腔压力,MPa;V1、V2分别为第1、第2活塞腔初始体积,mm3;Q1、Q2分别为第1、第2活塞腔与制动管路间的阀口流量,mm3/s;rm1、rm2分别为第1、第2活塞腔的泄漏系数;B为液体的体积弹性模量,MPa。
1.5 制动管路模型
建立制动管路动力学模型时主要考虑制动管路的可压缩性和管路阻力,并假设制动管内制动液的流动方式为层流,忽略制动液惯量。根据制动液的动力学方程得到:
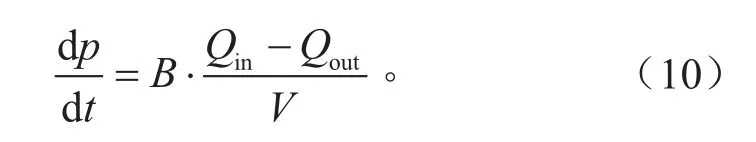
由于制动管路自身会扩张,制动液体积弹性模量已经无法完全反映制动液在管路中的运动特性,所以B不再是制动液体积弹性模量,而是制动液和制动管路有效体积弹性模量。
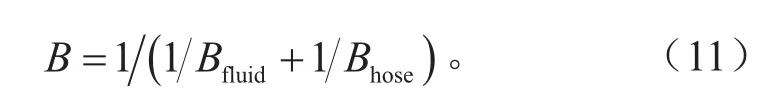
式中:B为有效体积弹性模量,MPa;Bfuid为制动液体积弹性模量,MPa;Bhose为制动管路体积弹性模量,MPa。
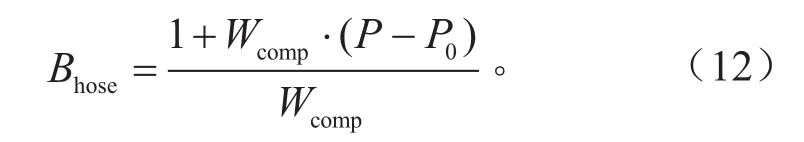
式中:P为制动管路压力,MPa;P0为制动管路初始压力,MPa;Wcomp为制动管路柔度,MPa-1,包括径向柔度和轴向柔度。
1.6 制动器模型
本研究以浮动钳盘式制动器为研究对象,并基于以下假设:不考虑钳体的变形;忽略制动块与制动器支架之间的摩擦;不考虑钳体内压力损失。
根据制动器的结构和工作原理,可将制动器的运动划分为3个阶段:
第1阶段,由于制动块与制动盘之间存在间隙Δ,压力建立较慢,此时内外制动块与制动盘之间的接触刚度和接触阻尼都不会起作用,活塞与内制动块一起运动,钳体与外制动块一起运动,xi<Δ。
内制动块与活塞的动力学方程为:
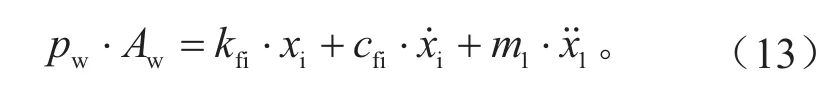
外制动块与钳体的动力学方程为:
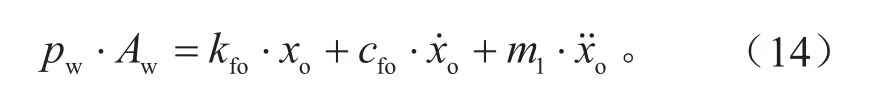
式中:pw为制动轮缸压力,MPa;Aw为制动轮缸内径,mm;kf为活塞与钳体密封圈之间的接触刚度,N/mm;cf为活塞与钳体密封圈之间的接触阻尼,N/(mm·s-1);kfo为钳体与支撑销之间的接触刚度,N/mm;cfo为钳体与支撑销之间的接触阻尼,N/(mm·s-1);m1为活塞与内制动块质量,kg;m2为钳体与外制动块的质量,kg;xi为内制动块位移,mm;xo为外制动块位移,mm。
第2阶段,由于内制动块与活塞质量之和远小于外制动块与钳体质量之和,由动量定理可知,当内制动块消除间隙Δ时,外制动块还未消除间隙Δ。第2阶段则为当内制动块消除间隙Δ时,外制动块消除间隙Δ,xi>Δ,xo>Δ。
内制动块与活塞的动力学方程为:
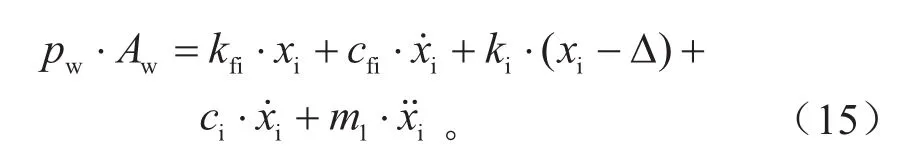
外制动块与钳体动力学方程为:
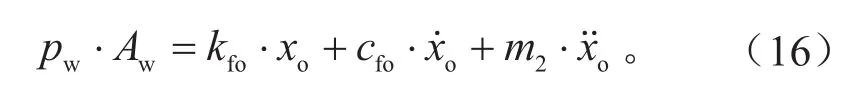
式中:ki为内制动块与制动盘之间的接触刚度,N/mm;ci为内制动块与制动盘之间的接触阻尼,N/(mm·s-1)。
第3阶段,当内外制动块都消除和制动盘之间的间隙Δ后,即xi>Δ,xo>Δ 。
内制动块与活塞的动力学方程为:
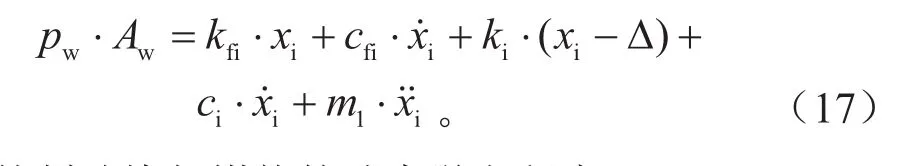
外制动块与钳体的动力学方程为:
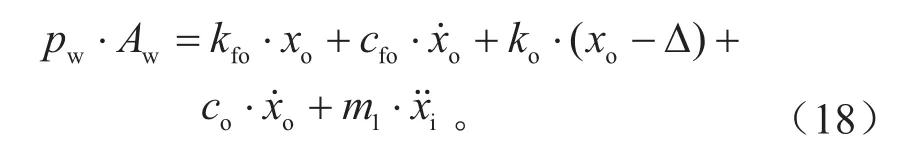
式中:ko为外制动块与制动盘之间的接触刚度,N/mm;co为外制动块与制动盘之间的接触阻尼,N/(mm·s-1)。
2 模型验证
基于上述对制动系统各零部件的结构与特性分析,构建了液压伺服制动系统的完整动力学模型,确定了不同零部件之间的运动学关系,为后续仿真模型搭建和踏板特性分析提供了理论基础。
2.1 仿真模型及试验平台
利用AMESim中的机械元件库、液压元件库、液压设计元件库及整车库,建立了制动系统的仿真模型,包括制动踏板模型、真空助力器模型、制动主缸模型、制动器模型、液压管路模型和整车模型,如图3所示。
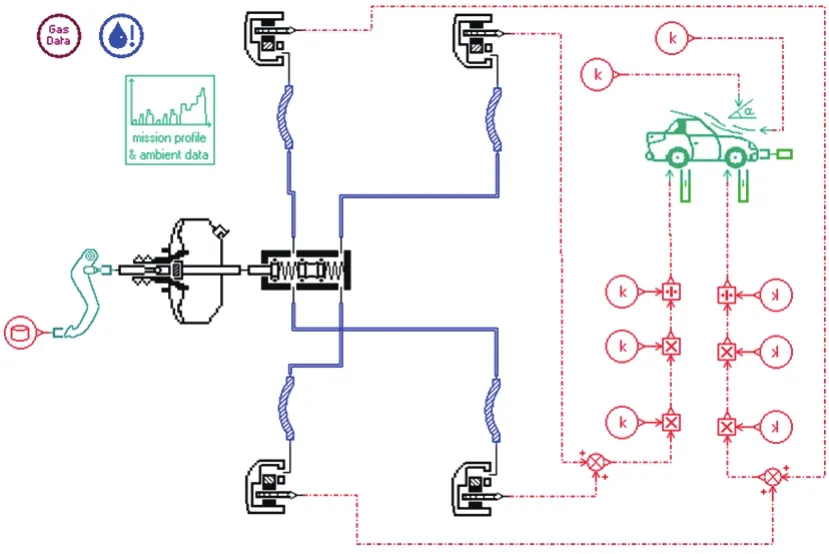
图3 制动系统仿真模型
考虑到模型验证的需要,对东风某型轿车的制动踏板性能展开实车试验。试验平台用到的传感器及数据采集工具见表1。最终将实测的踏板力和车速数据输入到仿真模型中,以此来研究仿真中的踏板力、踏板位移以及制动减速度三者间的对应关系。
为提高AMESim仿真结果的准确性和可靠性,对试验用车制动系统的相关零部件结构参数进行了测量与标定,最大限度地保证仿真模型预设参数与实车的一致。限于篇幅本文仅列出制动主缸的相关结构参数,见表2。
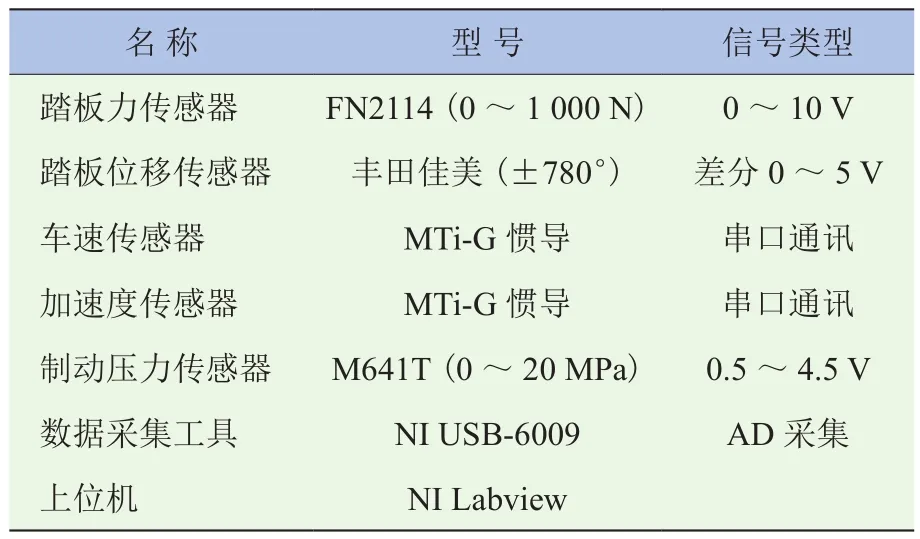
表1 实车测试平台

表2 制动主缸结构参数
2.2 静态仿真模型验证
踏板位移随踏板力的变化曲线如图4所示。由图可知,两条曲线整体上是比较相符的。仿真结果在踏板空行程上略大于试验结果,这主要是由于测量制动系统中的间隙时存在一定误差,包括真空助力器中橡胶阀门与控制阀座之间的间隙,控制阀柱塞与橡胶反作用盘之间的间隙等。其中,控制阀柱塞与橡胶反作用盘之间的间隙对该阶段影响最大。仿真结果在真空助力器达到最大助力点附近时,其踏板位移稍小于试验结果,这主要是由真空助力器橡胶反作用盘刚度的测量误差所导致。目前采用将一定量的砝码作用在橡胶反作用盘上,然后用游标卡尺测量砝码下降高度,再将测量的一系列力-变形点导入仿真模型。而橡胶反作用盘的刚度最好由专业机构测试更为准确。

图4 踏板位移与踏板力的关系曲线
制动管路压力随踏板力的变化曲线如图5所示。由图可知,仿真结果和试验结果一致性较好,这主要是因为管路压力主要与力和制动主缸截面面积有关,这两个参数都相对容易准确获得。仿真中的踏板输入力是直接将试验中采集的踏板力导入到模型中,真空助力器输出力主要与助力比有关,而助力比主要受橡胶反作用盘直径与控制阀柱塞直径影响,这两个参数利用游标卡尺能较好地测量。
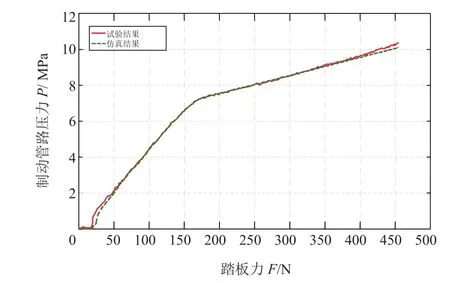
图5 管路压力与踏板力的关系曲线
2.3 动态仿真模型验证
动态试验中可以将车速和制动减速度考虑进来。制动减速度随踏板力的变化曲线如图6所示。由图可知,仿真结果与试验结果的一致性较好,试验结果仅在AB阶段减速度略小于仿真结果。这主要是由于试验时受场地距离的限制,驾驶员在踩踏离合器的同时进行制动,在制动初始阶段车辆的动力并未完全中断,导致制动减速度从正值开始下降。
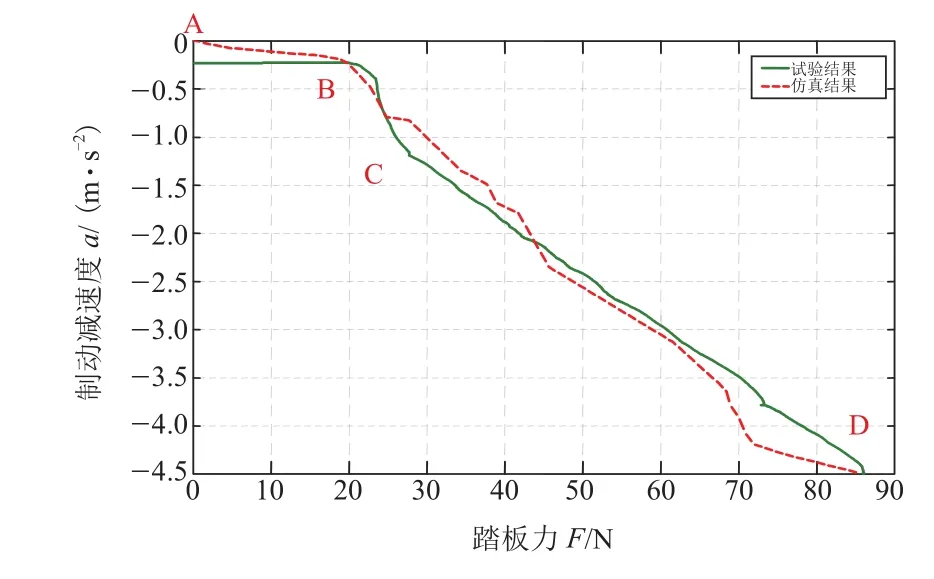
图6 制动减速度与踏板力的关系曲线
3 影响踏板特性的因素分析
影响制动踏板特性的因素有很多,包括主缸与轮缸的直径,真空助力器助力比,制动系统的内部间隙等[11-12]。考虑到制动踏板特性主要与力位曲线有关,本节基于上述建立的动力学模型和仿真模型,从制动系统弹性元件的 “变形”角度出发,主要研究橡胶反作用盘刚度以及制动软管变形对踏板特性的影响。
3.1 橡胶反作用盘刚度的影响
橡胶反作用盘是真空助力器产生助力的核心元件,其刚度值与踏板特性有密切关系,考虑到橡胶反作用盘是体积不可压缩的柔性材料,如1.2节所述,可以将其简化成一个液压缸,并且通过液压缸中的弹簧刚度来模拟橡胶反作用盘的刚度。橡胶反作用盘是变刚度的,不能直接将弹簧刚度设置为一定值。本文在试验测量的基础上,以表格的形式给出橡胶反作用盘刚度,见表3。不同橡胶反作用盘刚度下的踏板位移随踏板力的变化关系曲线如图7所示。橡胶反作用盘刚度对曲线的影响发生在AB、BC和CD三个阶段,在AB和BC两个阶段内,在相同的踏板力条件下,随着橡胶反作用盘刚度的增大,踏板位移逐渐增大,但增幅较小;在CD阶段内,在相同的踏板力条件下,随着橡胶反作用盘刚度的增大,踏板位移逐渐减小。此外,随着橡胶反作用盘刚度的增大,曲线圆弧过渡越平滑。
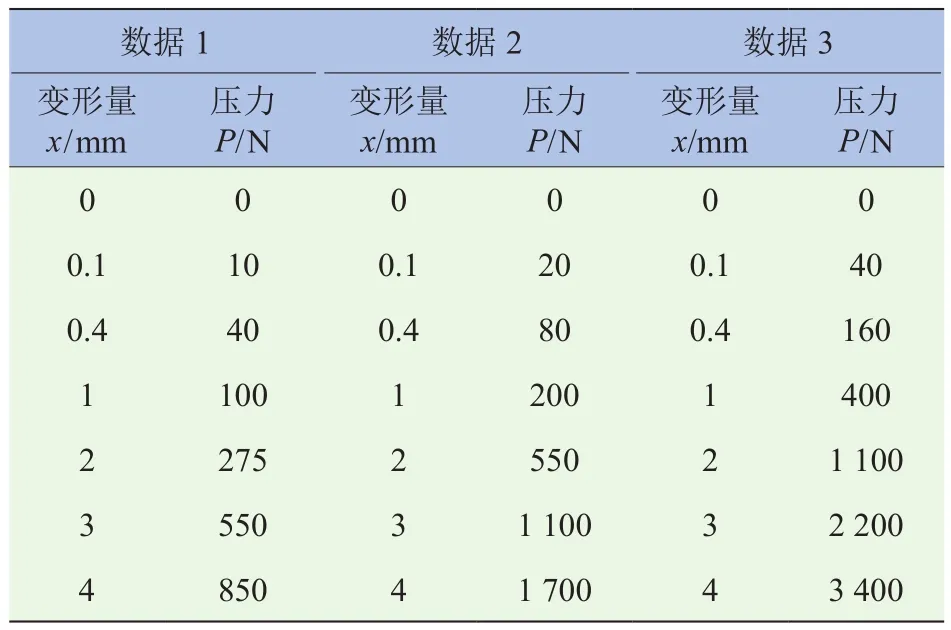
表3 橡胶反作用盘刚度
不同橡胶反作用盘刚度下的管路压力随踏板力的变化曲线如图8所示。橡胶反作用盘刚度对曲线的影响发生在AB和BC两个阶段,在这两个阶段内,在相同的踏板力条件下,随着橡胶反作用盘刚度的增大,管路压力逐渐增大;对CD阶段几乎没有影响。
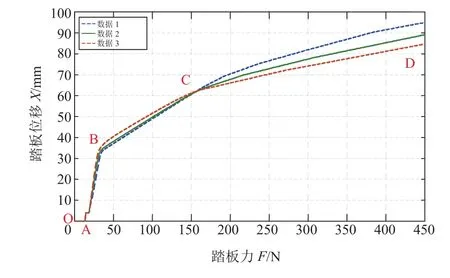
图7 踏板位移与踏板力的关系曲线
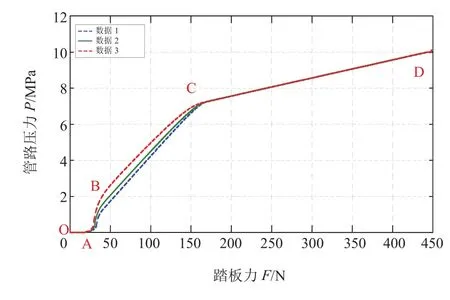
图8 管路压力与踏板力的关系曲线
3.2 制动软管变形的影响
制动压力从主缸传递到轮缸时必须经过制动软管,受温度和压力变化的影响,制动软管在车辆制动过程中会发生不同程度的变形,该变形会直接影响制动液流量与流速,从而影响制动踏板的特性。制动软管变形的难易程度可以通过体积模量来反映。影响制动软管体积弹性模量的参数包括制动管路内外径、泊松比和管路杨氏模量,本文主要研究管路杨氏模量对踏板特性的影响。不同制动软管杨氏模量下的踏板位移随踏板力的变化关系曲线如图9所示。制动软管杨氏模量对曲线的影响发生在BC和CD两个阶段,在这两个阶段内,在相同的踏板力条件下,随着制动软管杨氏模量的增大,踏板位移逐渐减小。对于OA和AB两个阶段,踏板位移随踏板力的变化曲线几乎不会产生影响。
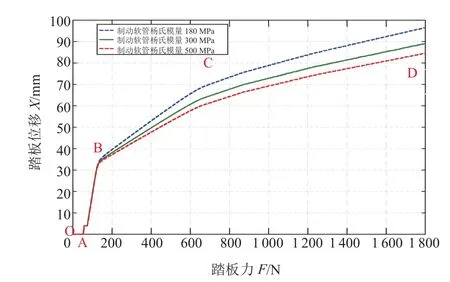
图9 踏板位移与踏板力的关系曲线
不同制动软管杨氏模量下的管路压力随踏板位移的变化关系曲线如图10所示。制动软管杨氏模量对曲线的影响发生在AB和BC两个阶段,在这两个阶段内,在相同的踏板位移条件下,随着制动软管杨氏模量的增大,制动管路压力也逐渐增大并且提前了AB和BC两个阶段间的转折点。
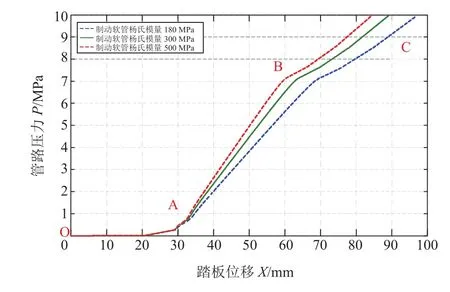
图10 管路压力与踏板位移的关系曲线
4 踏板感觉评价及优化
4.1 踏板感觉评价
制动踏板感觉直接影响驾驶员对车辆品质的评价,上文围绕制动踏板的建模与验证也是为了提高对踏板感觉的评价。这里采用美国通用汽车的BFI评价体系,对试验车辆在不同制动强度下的踏板力、踏板位移以及制动减速度等参数进行全面分析,原始的制动踏板感觉指数见表4。最终,BFI得分为71.61,表明还有较大的优化空间。该车得分率较差的参数主要是初始点制动踏板位移,正常制动至-4.9 m/s2时的踏板力和踏板位移,以及满载最大制动减速度时的踏板力等。
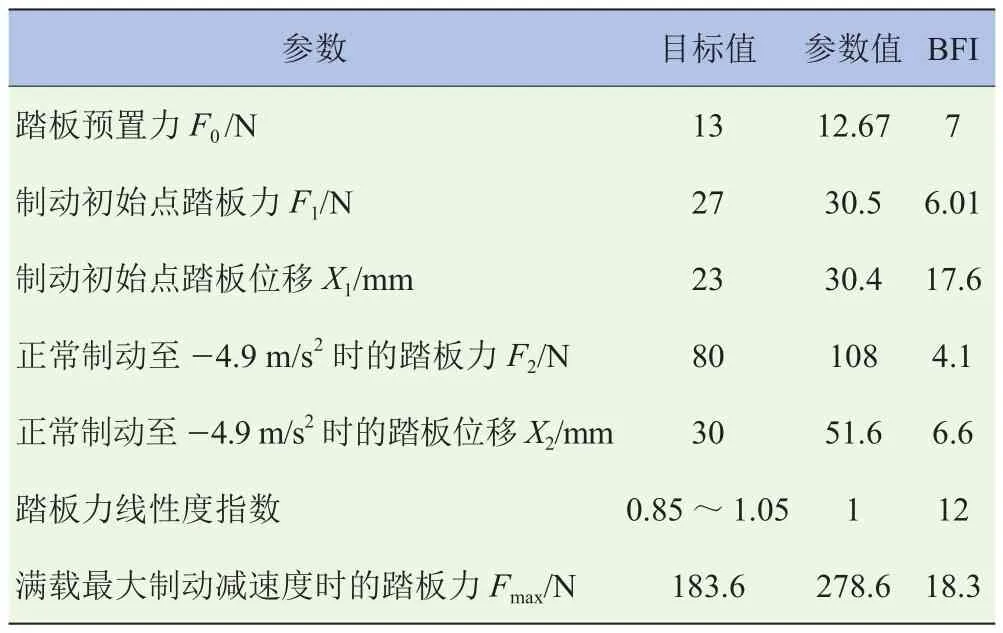
表4 原始的BFI
4.2 踏板感觉优化措施
本节主要针对上节中的低分项提出合理的优化措施。其中,制动初始点踏板位移取决于制动踏板空行程,而制动踏板空行程主要与制动系统间隙相关。由于橡胶反作用盘刚度对制动踏板空行程的影响并不明显,这里主要改进的是制动盘与制动块之间的间隙。考虑到制动间隙受制于制动性能指标的影响不能随意减小,因此将此间隙由0.15 mm减少至0.1 mm后,制动初始点的踏板特性改善明显,而正常制动至-4.9 m/s2以及满载最大制动时的踏板特性改善不大。BFI得分为84.91。
正常制动至-4.9 m/s2时,正处于真空助力器按助力比助力阶段。同时根据上节中的分析,增大制动软管杨氏模量以及橡胶反作用盘刚度,可以降低真空助力阶段一定减速度下的制动踏板位移。考虑将制动软管杨氏模量由180 MPa提高到500 MPa,橡胶反作用盘刚度提高到图7或图8中的第3组数据,可以进一步优化正常制动至-4.9 m/s2时的踏板特性。通过采取这两项措施进行改进,最终该车的BFI得分为96.8,改进后的BFI见表5。剩余的扣分项主要在满载最大制动减速度时的踏板特性,但是该工况一般并不常见。
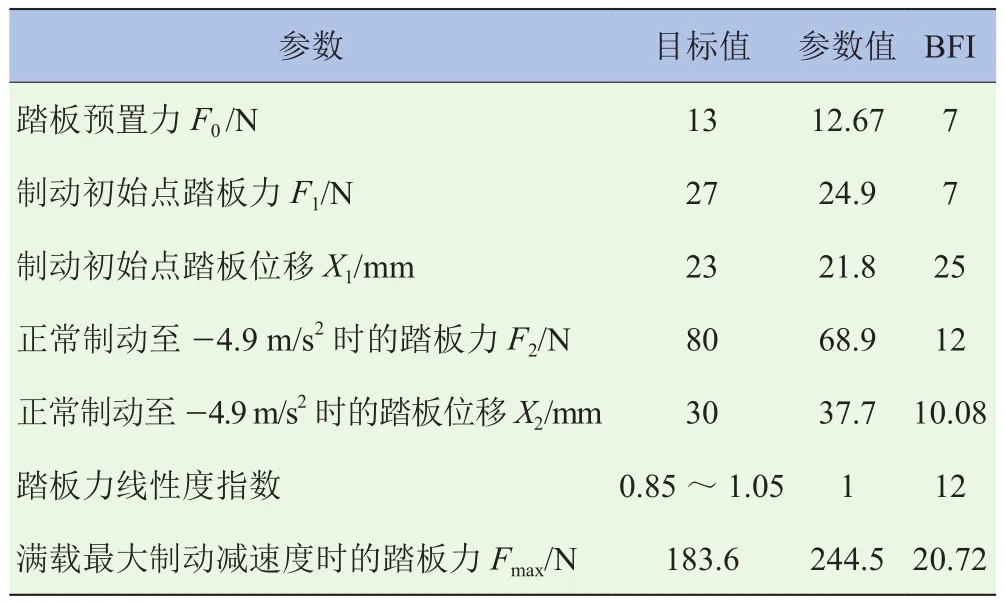
表5 改进后的BFI
5 结论
(1)基于模型分析了橡胶反作用盘刚度以及制动软管变形对踏板特性的影响,以此作为踏板感觉优化的基础。优化结果表明,通过减小制动盘与制动块之间的间隙,提高制动软管杨氏模量以及橡胶反作用盘刚度等措施,试验车辆的BFI评分从71.61提高到96.8。
(2)通过仿真与试验相结合的方式来研究制动踏板特性,既确保了结果的准确性,又缩短了研究周期。同时,所建立的动力学模型和仿真模型不仅适用于研究踏板特性,还能用于车辆一般制动性能的分析。
(3)除了本文所讨论的制动踏板影响因素,还有其它如制动温度上升、踏板踩踏速度等值得进一步深入研究。此外,某些零部件参数还需要通过更准确的测量来获得。
(
):
[1]PEREIRA J A D A. New Fiesta:Brake Pedal Feeling Development to Improve Customer Satisfaction [C]//SAE Technical Paper,2003-01-3598.
[2]EBERT D G,KAATZ R A. Objective Characterization of Vehicle Brake Feel[C]// SAE Technical Paper,940331,1994.
[3]花庆荣,陈士杰. 轿车制动感觉评估与制动感觉指数[J]. 上海汽车,2008(6):35-37,46. HUA Qingrong,CHEN Shijie. Vehicle Braking Sensation Evaluation and Braking Sensation Index [J]. Shanghai Automobile, 2008(6):35-37,46. (in Chinese)
[4]PASCALI L,RICCI C,CAVIASSO G. Customer Orientation:a Further Target in Brake System Design[C]// SAE Technical Paper,2003-01-0599.
[5]梁荣亮,王羽,谢晋中,等. 整车制动道路试验测试研究 [J]. 武汉理工大学学报(交通科学与工程版),2012,36(4):748-752,756. LIANG Rongliang,WANG Yu,XIE Jinzhong,et al. Research of Vehicle Brake Road Test [J]. Journal of Wuhan University of Technology(Transportation Science & Engineering),2012,36(4):748-752,756. (in Chinese)
[6]林志轩,高晓杰.制动踏板感觉研究现状[J]. 农业装备与车辆工程,2007(6):4-7,54. LIN Zhixuan,GAO Xiaojie. The Research Summarization of the Brake Pedal Feeling [J]. Agricultural Equipment and Vehicle Engineering,2007(6):4-7,54. (in Chinese)
[7]孟德建,张立军,余卓平. 乘用车制动踏板感觉台架试验研究 [J]. 汽车工程, 2014,36(12): 1488-1493. MENG Dejian,ZHANG Lijun,Yu Zhuoping. A Study on the Bench Test of Brake Pedal Feel for Passenger Car [J]. Automotive Engineering, 2014,36(12):1488-1493. (in Chinese)
[8]张抗抗,徐梁飞,华剑锋, 等. 后驱纯电动车制动能量回收系统及其策略的对比研究 [J]. 汽车工程,2015,37(2):125-131,138. ZHANG Kangkang,XU Liangfei,HUA Jianfeng,et al. A Comparative Study on Regenerative Braking System and Its Strategies for Rear-wheel Drive Battery Electric Vehicles [J]. Automotive Engineering,2015,37(2):125-131,138. (in Chinese)
[9]金智林,施瑞康,赵又群,等. 联合AMESim/Matlab的汽车制动踏板模拟器动态性能分析[J]. 重庆理工大学学报(自然科学版),2011,25(1):1-4. JIN Zhilin,SHI Ruikang,ZHAO Youqun,et al. Dynamic Analysis of Vehicle Brake Pedal Emulator Based on AMESim/Matlab [J]. Journal of Chongqing University of Technology (Natural Science Edition),2011,25(1): 1-4. (in Chinese)
[10]刘惟信. 汽车制动系的结构分析与设计计算[M]. 北京:清华大学出版社,2004. LIU Weixin. Structure Analysis and Design Calculation of Automobile Braking System [M]. Beijing:Tsinghua University Press,2004. (in Chinese)
[11]ZHANG Lijun,RUAN Cheng,MENG Dejian. The Infuence of Vacuum Booster Design Parameters on Brake Pedal Feel [C]// SAE Technical Paper,2014-01-2499.
[12]YOUNG K,AGNEW D. Investigation of the Relationship Between Wheel Diameter & Gross Vehicle Weight to Achieve Acceptable Brake System Performance[C]//SAE Technical Paper,2005-01-0792.
作者介绍
Simulation of Brake Pedal Characteristic and Optimization of Brake Pedal Feel
PEI Xiaofei1,DONG Xingzhi1,ZHANG Canming2,PAN Hao2,ZHANG Jie3
(1. Key Laboratory of Advanced Technology of Automotive Parts,Wuhan University of Technology,Wuhan 430070,China;2. Hubei Collaborative Innovation Center for Automotive Components Technology,Wuhan University of Technology,Wuhan 430070,China;3. Technology Center,Wanxiang Group,Hangzhou 311215,China)
In order to reveal the relationships among brake deceleration, pipe pressure, the brake pedal displacement and brake pedal force, a braking dynamic model for brake pedal feel was established. The corresponding static and dynamic simulation models were established in AMESim software and verified by experiments. The effects of the stiffness of the rubber reaction disk and the brake hose deformation on brake pedal feel characteristics were studied. The“BFI”evaluation system was used to evaluate the test vehicle and the optimization scheme was put forward. The optimization results show that the brake pedal feel can be significantly improved by many measures, such as reducing the gap between the brake disc and brake pads or increasing the Young’s modulus of the brake hose and the stiffness of the rubber reaction disk.
vehicle engineering; braking pedal; simulation model; pedal feeling optimization

裴晓飞(1985-),男,湖北武汉人。博士,讲师,硕士生导师,主要从事汽车制动系统及动力学研究。E-mail:peixiaofei7@163.com
U463.55
A
10.3969/j.issn.2095-1469.2017.01.08
2016-08-09 改稿日期:2016-09-01
国家自然科学基金青年项目(50515354)
用格式:
裴晓飞,董兴智,张灿明,等.汽车制动踏板特性仿真及踏板感觉优化[J]. 汽车工程学报,2017,7(1):052-060.
PEI Xiaofei,DONG Xingzhi,ZHANG Canming,et al. Simulation of Brake Pedal Characteristic and Optimization of Brake Pedal Feel [J]. Chinese Journal of Automotive Engineering,2017,7(1):052-060. (in Chinese)

