基于PCM编码的模拟信号数字化实现

郭 慧

(山西大学 商务学院 信息学院，山西 太原 030031)

基于PCM编码的模拟信号数字化实现

郭 慧

(山西大学 商务学院 信息学院，山西 太原 030031)

用A律13折线近似PCM编码的过程，总结了三种不同的计算思路，通过对极性码C1，段落码C2C3C4，段内码C5C6C7C8的计算，得到PCM的8位二进制编码、编码电平及编码量化误差。三种计算方法结果一致，表明了三种计算方法的有效性。最后，在MATLAB上对PCM编码进行了仿真，并总结了三种计算方法的特点，对PCM编码的计算及实现具有一定的借鉴意义。

PCM;MATLAB仿真;A律13折线;编码

0 引言

脉冲编码调制(Pulse Code Modulation, PCM)通信系统原理如图1所示[1]。

图1 PCM通信系统原理图

为了让模拟信号在数字通信系统上进行传输，在发送端需要进行模/数变换，在接收端需要进行反变换，即数/模变换。模拟信号数字化的三个步骤分别是抽样、量化和编码，具体步骤说明如表1所示[2]。把模拟信号数字化的过程称为PCM编码[3]。

量化的过程是近似模拟抽样值的过程，因此，存在量化误差。

表1 PCM编码步骤

1 计算方法

采用A律13折线[4]实现PCM编码。

已知：抽样值为+631△，求按照A律13折线编码的8位码、编码电平、解码电平和解码量化误差。采用A律13折线编码的相关取值如表2所示[5]。

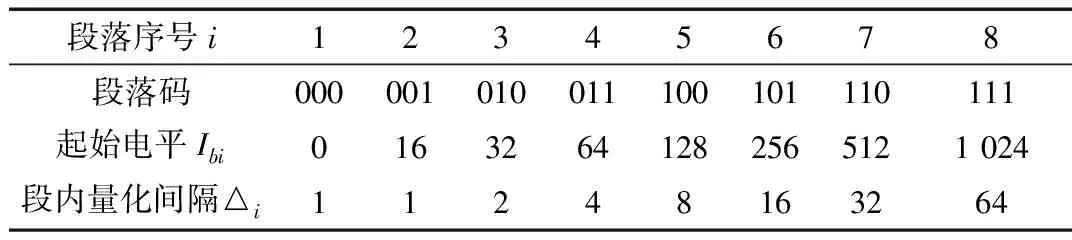
表2 A律13折线段落码及其对应的起始电平和量化间隔

1.1 逐次比较法

第1次比较：抽样值IS=+631△，C1=1。

第2次比较：串-并变化输出C2～C8为1000000，本地译码输出为：

IS2=128△

IS=+631△>IS2=128△，C2=1，位于第5段～第8段

第3次比较：串-并变化输出C2～C8为1100000，本地译码输出为：

Is3=512△

Is=+631△>Is3=512△，C3=1，位于第7段～第8段

第4次比较：串-并变化输出C2～C8为1110000，本地译码输出为：

Is4=1024△

Is=+631△

第5次比较：串-并变化输出C2～C8为1101000，本地译码输出为：

Is5=512△+[(1 024△-512△)/16*8=768△

Is=+631△

第6次比较：串-并变化输出C2～C8为1100100，本地译码输出为：

Is6=512△+[(1 024△-512△)/16*4=640△

Is=+631△

第7次比较：串-并变化输出C2～C8为1100010，本地译码输出为：

Is7=512△+[(1 024△-512△)/16*2=576△

Is=+631△>Is7=576△，C7=1

第8次比较：串-并变化输出C2～C8为1100011，本地译码输出为：

Is8=512△+[(1 024△-512△)/16*3=608△

Is=+631△>Is8=608△，C8=1

因此，编码C1C2C3C4C5C6C7C8为11100011，编码电平为608△，编码量化误差为631△-608△=23△。

1.2 分别比较法

极性比较：抽样值Is=+631△，C1=1

段落比较：512△<+631△<1 024△，位于第7段，C2C3C4=110

段内比较：631△-512△=119△<256△，C5=0

119△<128△，C6=0

119△>64△，C7=1

119△-64△=55△>32△，C8=1

因此，编码C1C2C3C4C5C6C7C8为11100011，编码电平=512△+(23*C5+22*C6+21*C7+20*C8)*[(1 024-512)/16]△=608△,编码量化误差为631△-608△=23△。

1.3 除以量化间隔法

极性比较与段落比较可以采用逐次比较法或分别比较法，C1C2C3C4=1110

段内比较：|抽样值-段落起始值|/量化间隔

量化间隔=(1 024-512)/16=32，|631-512|/32，商为3，余数为23,商转换为4位二进制，0011为所以C5C6C7C8为0011。

因此，编码C1C2C3C4C5C6C7C8为11100011，编码量化误差为余数23△。

2 MATLAB仿真实现

采用64位Windows 7操作系统，MATLAB2012a进行仿真实现。算法采用方法三，具体如下：

%判断极性

for i=1:n

if A(i)>=0

code(i,1)=1;

else

code(i,1)=0;

end

%确定段落码、量化间隔和起始电平

if abs(A(i))>=0&& abs(A(i))<16

code(i,2)=0; code(i,3)=0; code(i,4)=0;interval=1;start=0;

else if abs(A(i))>=16&& abs(A(i))<32

code(i,2)=0; code(i,3)=0; code(i,4)=1;interval=1;start=16;

else if abs(A(i))>=32&& abs(A(i))<64

code(i,2)=0; code(i,3)=1; code(i,4)=0;interval=2;start=32;

else if abs(A(i))>=64&& abs(A(i))<128

code(i,2)=0; code(i,3)=1; code(i,4)=1;interval=4;start=64;

else if abs(A(i))>=128&& abs(A(i))<256

code(i,2)=1; code(i,3)=0; code(i,4)=0;interval=8;start=128;

else if abs(A(i))>=256&& abs(A(i))<512

code(i,2)=1; code(i,3)=0; code(i,4)=1;interval=16;start=256;

else if abs(A(i))>=512&& abs(A(i))<1024

code(i,2)=1; code(i,3)=1; code(i,4)=0;interval=32;start=512;

else if abs(A(i))>=1024&& abs(A(i))<2048

code(i,2)=1; code(i,3)=1; code(i,4)=1;interval=64;start=1024;

end

%确定段内码

B=floor(abs(A(i)-start)/interval);

t=dec2bin(B,4)

code(i,5:8)=t(1:4);

end

仿真结果如图2所示。

图2反映了PCM的抽样及量化过程，通过比较发现，量化后的折线可以近似原始模拟信号线，但是量化后的取值和抽样的原始值之间存在误差。

3 结论

采用三种方法进行PCM编码，殊途同归，各种方法特点如下：

(1)逐次比较法，采用尝试策略，大于取1，否则取0，易于电路实现，思路简单。

图2 MATLAB仿真结果图

(2)分别比较法，采用三步走策略，将极性、段落码和段内码分别进行比较，极性与0比较，段落码与各段起止电平进行比较，段内码采用逐次比较的方法，大于比较值取1，否则取0，分别比较，清晰明了。

(3)除以段内间隔法，极性与段落码的比较同方法2，段内码采用除以段内间隔的方法，商转换为4位二进制编码。从本质上剖析了段内码的由来，计算过程简单，易于编程实现。

综上，对三种方法进行了总结，对PCM编码的计算和实现具有一定的借鉴作用。

[1] 王新良.现代通信技术概论[M].北京：机械工业出版社,2015.

[2] 李晓峰,周宁,周亮,等.通信原理(第2版)[M].北京：清华大学出版社,2014.

[3] SKLAR B.数字通信——基础与应用(第二版)[M].徐平平，宋铁成，叶芝慧，等，译.北京：电子工业出版社,2015.

[4] 赵守彬,李鸿刚.利用Matlab实现PCM编码的A律13折线法量化[J].科技信息,2009(36):231-232.

[5] 刘全金.一种A律PCM编码的简化方法[J].安庆师范学院学报(自然科学版),2007,13(4): 34-36.

Implementation of analog signal digitization based on PCM coding

Guo Hui

(School of Information, College of Business, Shanxi University, Taiyuan 030031, China)

With the encoding of A law 13 segments approximate PCM encoding, through the specific examples, this paper gives three different calculation methods and processes. Through the calculation of polar code C1, the code section C2C3C4, and code segment C5C6C7C8, it concludes the PCM 8-bit binary coding, coding level and coding quantization error. The results of the three methods are consistent, and the results show that the three methods are effective. Finally, the PCM code is simulated on MATLAB, and the characteristics of the three calculation methods are summarized, which can be used for reference for the calculation and implementation of PCM coding.

PCM; MATLAB simulation; A law 13 segments; encoding

TP914

A

10.19358/j.issn.1674- 7720.2017.02.021

郭慧.基于PCM编码的模拟信号数字化实现[J].微型机与应用，2017,36(2)：70-71,77.

2016-07-31)

郭慧(1980-)，通信作者，女，硕士，讲师，主要研究方向：网络通信与人工智能。E-mail：guozihui80@163.com。