广义Fibonacci数列的倒数和

张 福 玲

(渭南师范学院 数理学院，陕西 渭南 714099)

【自然科学基础理论研究】

广义Fibonacci数列的倒数和

张 福 玲

(渭南师范学院 数理学院，陕西 渭南 714099)

广义Fibonacci数列;倒数;有限和

近几年,不少学者对Fibonacci数列的倒数和进行了研究，并且取得了一些研究成果：

文献[3]研究得到

本文在上述研究的基础上，得到了广义Fibonacci数列倒数和的4个结论：

1 引理及其证明

证明 由广义Fibonacci数列的定义可得通项公式为:

根据通项公式有:

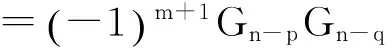
同理可得

引理2 GmGn+Gm+1Gn+1=Gm+n+1。

若令引理2中m=n，可得引理3

证明 由引理3可得

=G2n+1-G2n-1=aG2n。

引理5 Gn+1Gn+2-Gn-1Gn=aG2n+1。

证明 由递推公式和引理2可得

G2n+1=Gn-1Gn+1+GnGn+2，

那么

aG2n+1=aGn-1Gn+1+aGnGn+2

=Gn+1Gn+2-GnGn-1。

2 定理的证明

证明 由引理1可得

G2k-2G2k+1=G2k-1G2k-a，

(1)

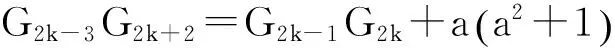
(2)

由引理5可得

aG4k+1=G2k+1G2k+2-G2k-1G2k，

(3)

aG4k-3=G2k-1G2k-G2k-3G2k-2，

(4)

根据式(1)-(4)

(5)

所以

因此

(6)

同理, 根据式(1)-(4)

因为

那么

(7)

即

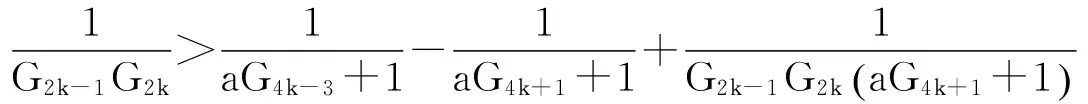
因此

由引理4可知

所以

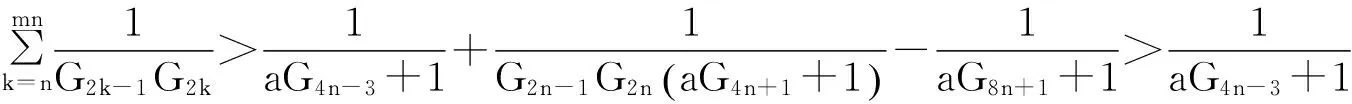
(8)

由式(6)(8)可知

所以定理1成立。

证明 由式(5)可知

(9)

由式(7)可知

(10)

根据式(9)(10)可知推论1成立。

证明 由引理1可得

G2k-1G2k+2=G2kG2k+1+a，

(11)

(12)

由引理5可得

aG4k-1=G2kG2k+1-G2k-2G2k-1，

(13)

aG4k+3=G2k+2G2k+3-G2kG2k+1。

(14)

根据式(11)-(14)

(15)

所以

因此

由引理4可知

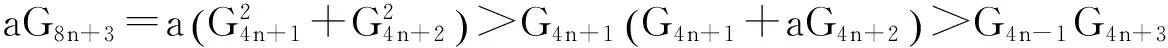
所以

(16)

同理, 根据式(11)-(14)有

因为

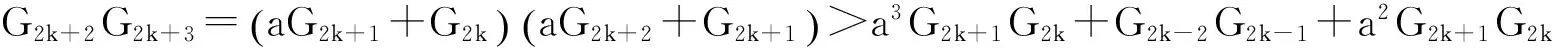
那么

(17)

即

那么

(18)

由式(16) (18)可知

因此定理2成立。

证明 由式(15)可知

(19)

由式(17)可知

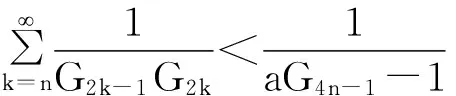
(20)

根据式(19)(20)可知推论2成立。

[1] H.Ohtsuka, S.Nakamura. On the sum of reciprocal Fibonacci numbers[J].The Fibonacci Quarterly，2008,46(2):153-159.

[2] 吴振刚，王婷婷.关于斐波那契数列倒数的有限和[J].内蒙古师范大学学报(自然科学汉文版),2011，40(2):125-128.

[3] 王婷婷.Fibonacci数列倒数的无穷和[J].数学学报(中文版),2012，55(3):517-524.

[4] Zhang Guojie.The Infinite Sum of Reciprocal of the Fibonacci Numbers[J].Journal of Mathematical Research and Exposition，2011,31(6):1030-1034.

[5] Sarah H. Holliday, Takao Komatsu. On the Sum of Reciprocal Generalized Fibonacci Numbers[J].Integers，2011,11(4):441-455.

【责任编辑 牛怀岗】

The Finite Sums of the Generalized Fibonacci Number

ZHANG Fu-ling

(School of Mathematics and Physics,Weinan Normal University, Weinan 714099, China)

generalized Fibonacci numbers; reciprocal; finite sum

O157

A

1009-5128(2017)04-0011-05

2016-11-22

陕西省教育厅专项科研计划项目：广义Fibonacci数列性质与若干变换的研究(2015JK1262)；渭南师范学院科研计划项目：Lucas数中素因子指数下标的关系研究(14YKP008)

张福玲(1970—),女,陕西渭南人，渭南师范学院数理学院副教授，主要从事数论研究。