Origin自定义函数拟合在分析土壤吸附等温模型中的应用

孟佩佩

(暨南大学 环境学院， 广东 广州 510632)

Origin自定义函数拟合在分析土壤吸附等温模型中的应用

孟佩佩

(暨南大学 环境学院， 广东 广州 510632)

由于吸附等温线线性拟合存在着随意性和误差性，因此在土壤对铜的吸附测试的实验数据中，Freundlich吸附等温线性模型的处理方法可能存在着不足。为此，提出了利用Origin自定义函数拟合非线性吸附等温模型，如Langmuir、Freundlich、Temkin、Redlich-Peterson、Koble-Corrigan和Toth模型，不但可以消除线性模型所带来的误差，而且可以让学生更全面地理解吸附等温模型，学会用Origin自定义函数拟合功能对实验数据进行更科学的处理。

土壤； 吸附等温模型; Origin函数

环境中的重金属元素所具有的自净能力和环境容量的原因之一在于土壤的吸附性能[1]。土壤对重金属离子的吸附主要分为专性吸附和电性吸附[2],前者是胶体表面与被吸附离子间通过共价键而产生的；而后者则是土壤胶体通过静电引力引起的吸附[3]。然而,土壤对重金属的吸附行为还受到外界因素影响，非常复杂,这些影响因素主要是指土壤理化特性、土壤有机无机组分、土壤溶液组成和pH等[4]，pH是影响铜在土壤中吸附行为的重要因素[5]。土壤的有机质如腐植酸,因含有多种功能基团可与土壤中重金属发生相互作用[6],从而增强铜在土壤的吸附能力[7]。在我们的环境化学实验课中,“土壤对铜的吸附测试”的实验就是探讨不同的pH值和有无添加腐植酸的条件下,土壤对铜离子的吸附性能变化。

1 6种等温吸附模型

到目前为止,有关重金属离子浓度对土壤吸附行为的影响,仍然是集中在吸附等温线的研究[8]。经典的吸附等温线模型是Langmuir和Freundlich模型。Langmuir模型属于单分子层吸附模型,即在吸附过程中,吸附剂表面均匀,吸附是单分子层的,各处的吸附能相同,且在吸附剂表面上的各个吸附点间没有吸附质的转移运动[9]。很显然,Langmuir模型是一种非常理想吸附的模型。Freundlich模型则是描述吸附剂表面不均匀以及吸附热不均匀分配的吸附行为,也就是在非理想状态下非均相表面的多层吸附过程,吸附热随吸附量呈对数形式降低[9]。另一种常用的Temkin模型,所描述的是在吸附剂吸附溶质时,若溶质间发生交互作用力,则必会对等温吸附行为产生影响，其能量关系是吸附热随着分子的覆盖而线性降低[10]。Freundlich模型和Temkin模型都适用于不均匀表面吸附。一般,在研究Langmuir、Freundlich、Temkin模型时,经常采用这3种模型的线性方程来拟合分析。

有研究却指出,线性吸附等温模型不是一个很好的拟合办法,因为线性模型缺乏一个合理的标准,其形式随意性很大,任何一个改变都会导致结果发生变化。例如,运用Langmuir线性模型拟合时,误差有时会达到50%，甚至更高[11]。因此,考虑到吸附等温线线性拟合的随意性和误差性,应该使用非线性方法来描述土壤对铜的吸附行为,这是因为非线性拟合的实质就是一个试错过程,通过对一些可变参数的预赋值,并在设定目标值的指引下,不断试错、赋值以找到接近于目标值的参数,这就有效地避免了线性拟合的缺点。而且,除了Freundlich模型外,还有一些有用的吸附等温非线性模型可以使用,这些模型可以弥补经典模型的不足,但是这些模型的参数超过2个,用线性拟合的方法无法处理,因此必须通过非线性拟合方法来实现。例如,Redlich-Peterson吸附模型,它克服了Freundlieh模型受低浓度的限制和Langmuir模型受高浓度的限制,而提出较合理的经验方程式,它的方程具有Langmuir方程和Freundiich方程的特征,因而具有3个参数[9]。Koble-Corrigan模型也是 Langmuir模型和 Freundlich模型中各要素的结合,属于一个经验性模型,也具有3个参数的特征[9]。还有Toth模型,它假设溶质与吸附剂间的吸附能是拟高斯分布,并由位能理论导出,适用于非均态吸附系统[9]。上述的6种等温吸附模型的方程和参数见表1。

表1 等温吸附模型[9-10]

表1(续)

针对非线性模型的拟合,Origin 软件已经成功用于对数据点的非线性拟合和数据绘图。在现有各种Origin版本中,已经提供超过200种的函数供用户使用,其中包括Langmuir模型和Freundlich模型函数。尽管如此,Origin函数库里仍然缺少一些有用的函数,例如等温吸附模型中的Redlich-Peterson、Koble-Corrigan以及Toth函数方程。因此,必须在Origin软件中,利用自定义函数拟合功能,在其函数库里构建需要的函数并加以应用。

本文主要是基于“环境化学实验”中土壤对铜的吸附测试的实验数据,通过Origin软件的自定义函数拟合方法,实现6种常用的非线性吸附等温模型的拟合,并在拟合结果的基础上,再次探讨土壤对铜离子的吸附行为机理。

2 Origin自定义函数拟合方法

2.1 自定义函数构建

在Origin8.5的操作窗中(见图1),打开“Tools”选单中的“Fitting Functions Organizer”拟合函数管理器(见图2),先单击“New Category”建好新的目录,再单击“New Function”自定义函数名,如“Langmuir”。建好后,可以在窗口左侧的下拉条中找到,此时便可以开始进行函数构建。构建流程大致如下:分别定义 “Independent Variables”(自变量)为“x”, “Dependent Variables”(因变量)为“y”,拟合时确保吸附数据对应“x”和“y”；将“Parameter Names”的参数修改为“a, b, c”等(可任意设置参数名以及数目)；然后可在“Function”里进行函数构建(构建过程中要正确运用运算符号)。

构建好函数后,必须使函数成为Origin系统的一部分,即添加到Origin函数库里。通过点击窗口里右边的“Builder…”,在新的窗口完成即可,然后点击“Save”保存构建好的函数,并可以通过单击“Simulate”来初步模拟函数。最后,单击“OK”完成自定义函数构建工作。

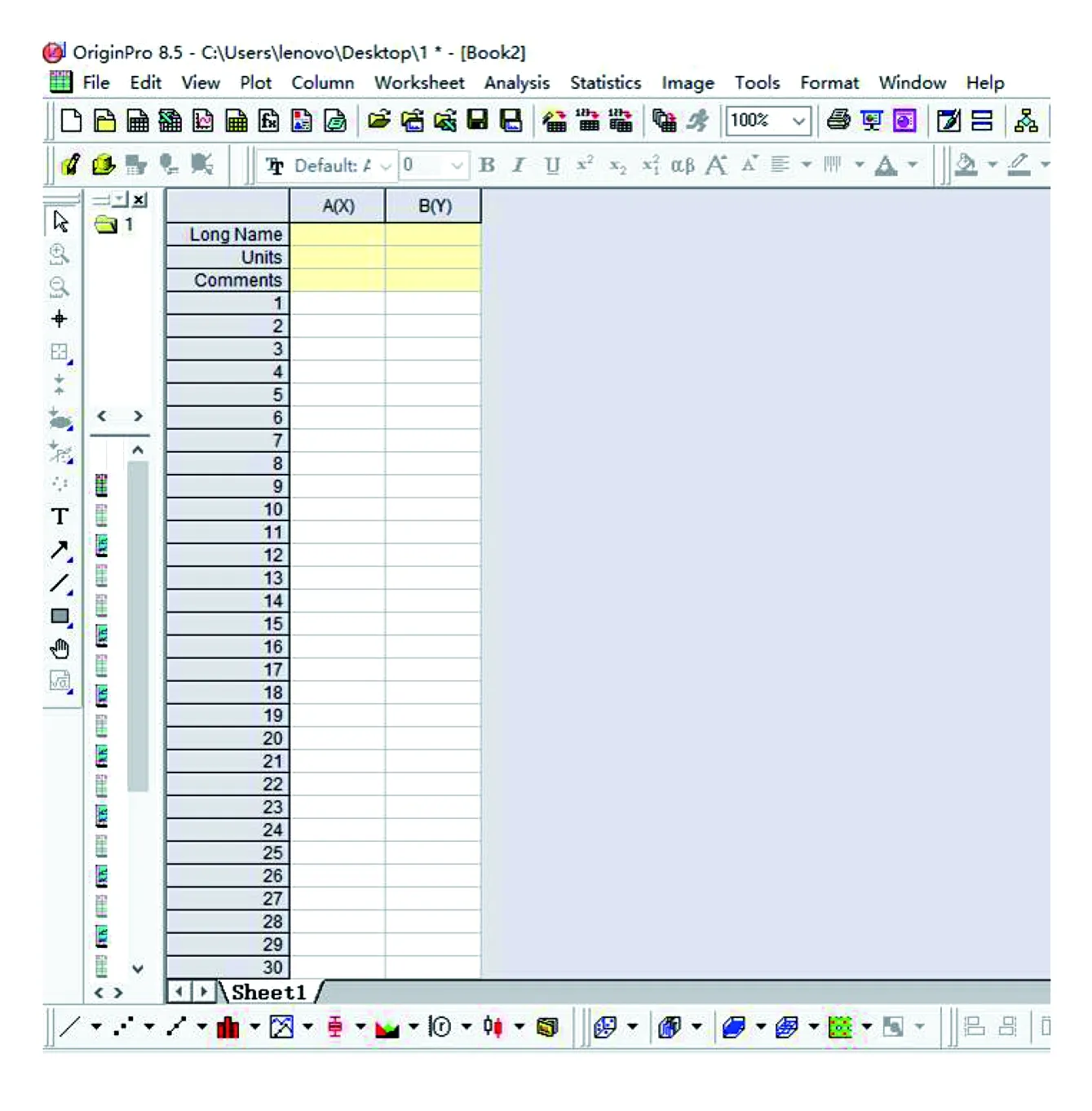
图1 Origin8.5的操作窗

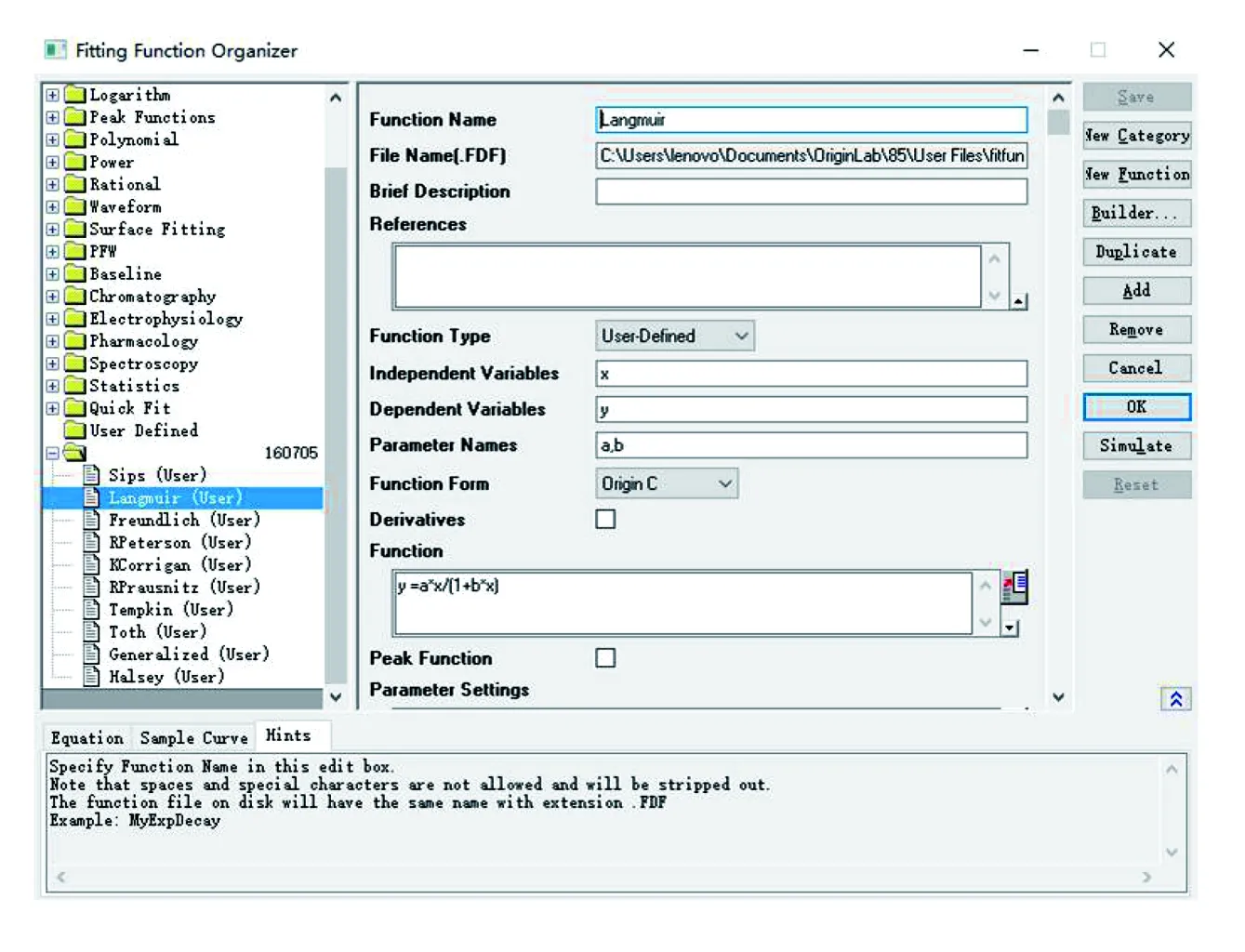
图2 “Fitting Functions Organizer”拟合函数管理器窗口

2.2 函数拟合

在图1的Origin8.5的操作窗中,导入实验获得的吸附数据(注意对应“x”和“y”),同时做散点图。选择“Analysis”选单(菜单)中的“Nonlinear Curve Fit”(NLFit对话框)(见图3)。在“Category”中找到之前建好的目录,并在“Function”里找到之前构建好的函数,可开始进行拟合。为了得到更有效的结果,建议单击对话框里的“Parameters”(见图4),在“Value”里输入自定义的参数原始值(随便设置)；然后单击对话框里的“Fit Until Converaged”(图3中红色字体下方的从左到右数第10个按钮),即进行拟合直到数据收敛。待收敛完成后,可得到将“Parameter Names”的参数修改为“a, b, c”等参数值,并完成拟合,并同时在吸附数据的散点图上得到拟合曲线。

图3 “Nonlinear Curve Fit”对话框

图4 对话框里的“Parameters”

3 实验

实验方法见文献[12]中的实验——土壤对铜的吸附测试。

3.1 实验材料与仪器

材料:烧杯,容量瓶,聚乙烯塑料瓶,移液管,土壤样品(自制),腐殖酸,二氯化钙(CaCl2),硫酸(H2SO4),氢氧化钠(NaOH)溶液,铜储备溶液(1 000 mg/L):用硝酸铜配制；铜标准溶液(50mg/L,购买)；铜系列溶液(40.00、60.00、80.00、100.00、120.00mg/L)(先通过移取不同体积的铜标准溶液于烧杯中,再加入CaCl2溶液稀释至相应体积,然后用H2SO4溶液和NaOH调节pH =2.5和5.5,再将此溶液移入容量瓶中,最后用CaCl2溶液定容)；

仪器:原子吸收分光光度计(PerkinElmer PinAAcle900T，恒温振荡器,离心机以及pH计。

测试条件:波长324.75 nm,灯光流15 mA,狭缝宽0.7 nm,燃气-乙炔 ,助燃气-空气,燃气流速为2.5 L/min,助燃气流速10 L/min)、

3.2 实验

(1) 吸取50 mg/L的铜标准溶液0.00、0.50、1.00、2.00、4.00、6.00、8.00、10.00 mL分别置于50 mL比色管中,再滴加2滴0.5 mol/L的H2SO4,并用纯水定容,其浓度分别为0、0.50、1.00、2.00、4.00、6.00、8.00、10.00 mg/L；然后在原子吸收分光光度计上测定吸光度，根据吸光度与浓度的关系绘制标准曲线。

(2) 分别称取土壤样品10份(1 g/份),置于聚乙烯塑料瓶中；依次加入一定体积的、pH值为2.5和5.5、不同浓度的铜系列溶液,盖上瓶塞后置于恒温振荡器上；振荡一定时间后,吸附达到平衡；取15 mL土壤浑浊液于离心管中,离心10 min,吸取上层清液10 mL于50 mL比色管中,加入2滴的H2SO4溶液,并用纯水定容；然后用原子吸收分光光度计测定吸光度,对应标准曲线获得样品的实际浓度(Cep),每个样品做3个平行样。土壤对铜的吸附量可通过以下式计算[13]:

其中,qep为土壤对铜的吸附量(mg/g)；C0为溶液中铜的起始浓度(mg/L)；Cep为溶液中铜平衡浓度(mg/L)；V为溶液的体积(mL)；m为烘干土壤质量(g)。

以吸附量(qep)和浓度(Cep)数据输入Origin中对应的“x”和“y”,即可拟合不同pH条件下土壤对铜的等温吸附线。

4 拟合结果与吸附机理讨论

4.1 Langmuir、Freundlich、Temkin吸附等温模型拟合

图5 Langmuir与Freundlich等温吸附模型拟合曲线

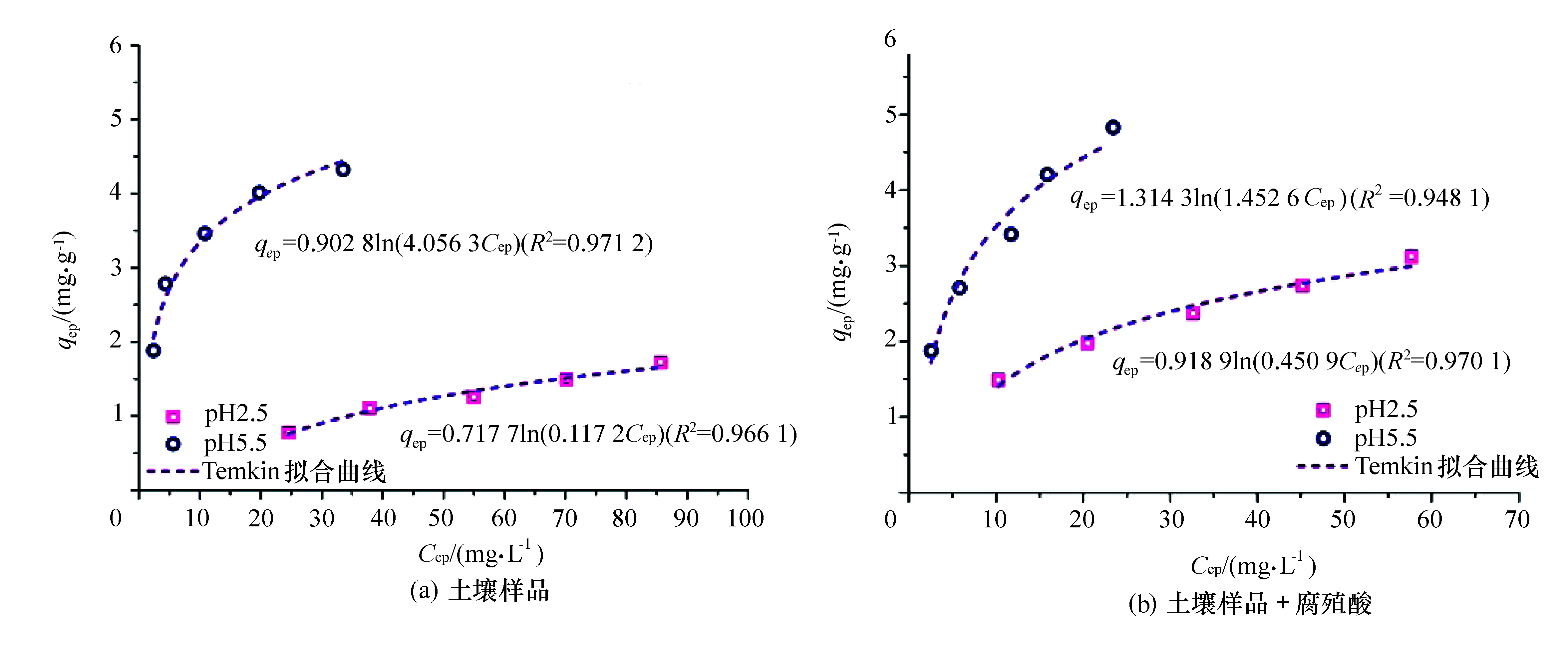
图6 Temkin等温吸附模型拟合曲线

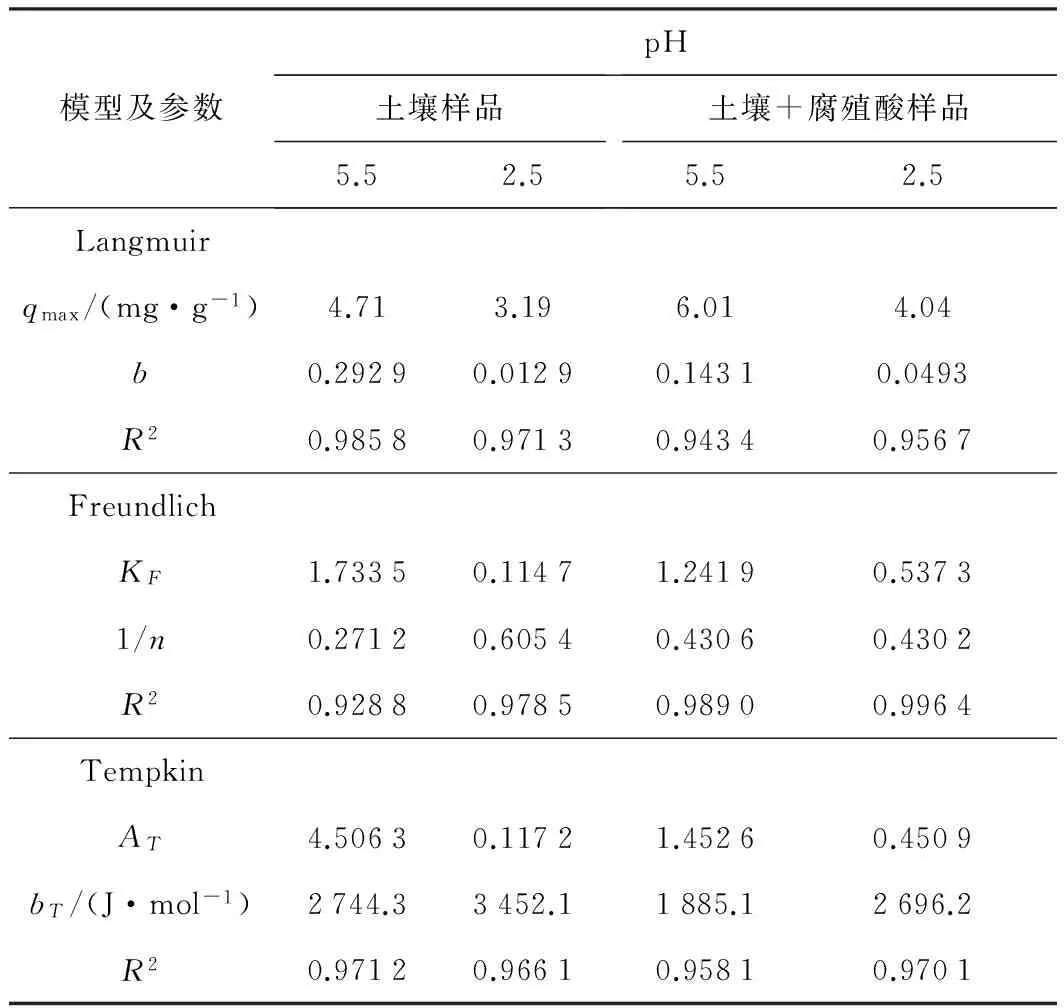
模型及参数pH土壤样品5.52.5土壤+腐殖酸样品5.52.5Langmuirqmax/(mg·g-1)4.713.196.014.04b0.29290.01290.14310.0493R20.98580.97130.94340.9567FreundlichKF1.73350.11471.24190.53731/n0.27120.60540.43060.4302R20.92880.97850.98900.9964TempkinAT4.50630.11721.45260.4509bT/(J·mol-1)2744.33452.11885.12696.2R20.97120.96610.95810.9701

4.2 Redlich-Peterson、Koble-Corrigan、Toth吸附等温模型拟合

Redlich-Peterson、Koble-Corrigan、Toth吸附等温模型使用不多,因为它们属于3参数的模型,但是这些模型还是有用的,主要是用来验证吸附行为与Langmuir、Freundlich模型的关系。Redlish-Peterson模型是结合受低浓度限制的Freundlich模型和受高浓度限制的Langmuir 模型而提出的较合理模型。在Redlish-Peterson模型参数里,当常数g趋近于 1,意味着吸附趋向于Langmuir 模型,此时方程中的参数B相当于Langmuir模型的b[15]；而 Freundlich模型是当 Redlich-Peterson 方程的参数A和B远大于1时的特例[16]。

Koble-Corrigan模型参数n值接近1,表明Koble-Corrigan模型接近Langmuir形式[10]；而n介于0和1之间时表明Koble-Corrigan模型与Langrnuir模型相差较大,具有Langmuir模型和Freundlich模型的共同特征。

在Toth模型中,参数btoth和β1是经验系数,当β1趋向于1时,方程趋向Langmuir模型方程,而偏离1的程度越大,则说明吸附剂表面越不均匀。

利用Oringin软件对这3种模型进行非线性模型拟合,拟合得到的曲线及模型方程如图7、图8和图9所示,拟合的模型参数见表3。由表3中的相关性(R2均大于0.96)可知,这3种模型也比较适合用来描述土壤对铜的吸附行为。在Redlish-Peterson拟合曲线参数中,在弱酸性条件下纯土壤样品的g趋近于 1,说明吸附趋向于Langmuir 模型；在强酸性条件下纯土壤样品以及任何条件下土壤+腐殖酸样品的g较小,A和B值远大于1,则说明吸附倾向于Freundlich模型,印证了之前的拟合结果。在Koble-Corrigan拟合曲线参数中,在弱酸性条件下纯土壤样品n最接近于 1,表明模型接近Langmuir形式；在强酸性条件下纯土壤样品以及任何条件下土壤+腐殖酸样品的n介于0和1之间,则表明还应具有Freundlich模型的特点。同理在Toth拟合曲线参数中的经验系数β1值也证明了之前的拟合结果。

5 结语

土壤对铜的吸附测试是环境化学实验课程中比较基础的一个实验,但是在对实验数据进行Freundlich线性模型拟合时,机理解释不够充分,且方法也不够全面,所得到的线性方程存在着一定的随意性和误差性。为了让学生理解更多的吸附等温线及其相关机理,并能更好地处理吸附实验数据,利用Origin自定义函数拟合更多的非线性吸附等温模型,有助于学生加深对该实验的理解,并更全面地掌握吸附操作这一实验技能。

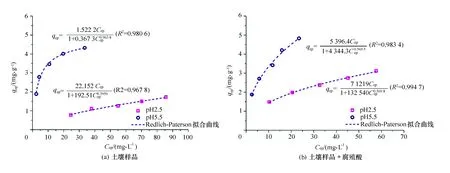
图7 Redlich-Peterson等温吸附模型拟合曲线

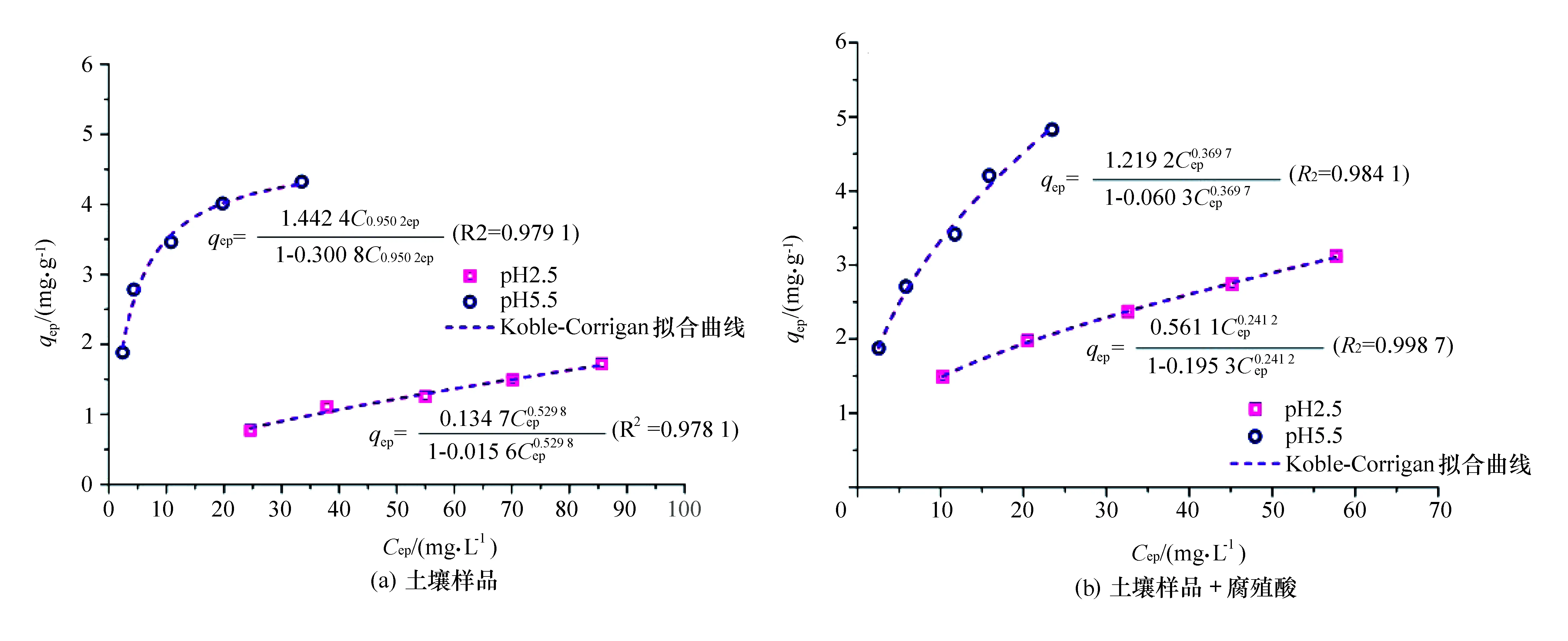
图8 Koble-Corrigan等温吸附模型拟合曲线

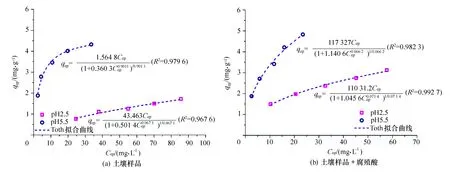
图9 Toth等温吸附模型拟合曲线

模型及参数pH土壤5.52.5土壤+腐殖酸5.52.5Redlich-PetersonA1.522222.1525396.471219B0.3673192.514344.3132540g0.96380.39500.56950.5698R20.98060.96780.98340.9947Koble-CorriganaK1.44210.13471.21920.5611bK-0.3008-0.0156-0.0603-0.1953n0.95020.52980.36970.2412R20.97910.97810.98410.9987TothKT1.564843.463111732711031.2btoth0.36030.50141.14061.0456β10.90110.06710.06620.0714R20.97960.96760.98230.9927

References)

[1] 李学垣. 土壤化学[M]. 北京: 高等教育出版社, 2001.

[2] 于天仁. 土壤化学原理[M]. 北京: 科学出版社, 1987:246-324.

[3] 罗洪亮, 周剑, 黄钊. 有机酸对几种土壤吸附铜的影响[J]. 中国岩溶, 2002，21(3):160-164.

[4] 张磊, 宋凤斌. 土壤吸附重金属的影响因素研究现状及展望[J]. 土壤通报, 2005,36(4):628-631.

[5] Muhammad A A, David A D. Effects of simple organic acids on sorption of Cu2+and Ca2+on goethite [J]. Geochimica et Cosmochimica Acta, 1996, 60(2):291- 304.

[6] 王擎运, 赵炳梓, 张佳宝,等. 胡敏酸和柠檬酸对铜在土壤中吸附-解吸行为的影响[J]. 农业环境科学学报, 2008,27(2):583-589.

[7] Arias M, Barral M T, Mejuto J C. Enhancement of copper and cadmium adsorption on kaolin by the presence of humic acids[J]. Chemosphere, 2002, 48:1081-1088.

[8] 邹献中, 张超兰, 宁建凤,等. 不同浓度铜离子土壤的吸附-解吸行为:兼论弱专性吸附态的存在[J]. 土壤学报,2012，49(5):892-900.

[9] Febrianto J, Kosasih A N, Sunarso J,et al. Equilibrium and kinetic studies in adsorption of heavy metals using biosorbent: a summary of recent studies [J]. J Hazard Mater,2009,162:616-645.

[10] Gupta S, Babu B V. Utilization of waste product (tamarind seeds) for the removal of Cr (VI) from aqueous solutions: equilibrium, kinetics, and regeneration studies[J]. J Environ Manage,2009,90:3013-3022.

[11] Harter R D, Baker D E. Applications and Misapplications of the Langmuir equation to soil adsorption phenomena[J]. Soil Sci Soc Am J, 1977,41(6):1077-1080.

[12] 董德明, 朱利中. 环境化学实验[M]. 北京: 高等教育出版社,2009.

[13] Zheng L, Meng P. Preparation, characterization of cornstalk xanthates and its feasibility for Cd (II) removal from aqueous solution[J]. J Taiwan Inst Chem E,2016,58:391-400.

[14] Aksu Z, Karabbayr G. Comparison of biosorption properties of different kinds of fungi for the removal of Gryfalan Black RL metal-complex dye[J]. Bioresour Technol,2008,99:7730-7741.

[15] Ho Y S, Ofomaja A E. Biosorption thermodynamics of cadmium on coconut copra meal as biosorbent[J]. Biochemical Engineering Journal, 2006,30(2):117-123.

[16] Ho Y S. Selection of optimum adsorption isotherm[J]. Carbon, 2004,42(10):2115-2116.

Application of Origin self-defined function fitting to analysis of soil adsorption isotherm model

Meng Peipei

(College of Environment, Jinan University, Guangzhou 510632, China)

Due to the existence of the randomness and error in the linear fitting of adsorption isotherm, the deficiencies may exist in the treatment method of Freundlich adsorption isotherm linear model according to the experimental data of adsorption test of copper in soil. For this reason, it is proposed to use the nonlinear adsorption isotherm models of Origin self-defined function fitting such as Langmuir, Freundlich, Temkin, Redlich-Peterson, Koble-Corrigan and Toth, which can not only eliminate the error caused by the linear models, but also help the students to understand isotherm models more comprehensively, and learn how to apply the function of Origin self-defined function fitting to more scientific treatment of experimental data.

oil; adsorption isotherm model; Origin function

10.16791/j.cnki.sjg.2017.01.016

2016-07-14 修改日期：2016-09-13

国家自然科学基金项目(51508206)；广东省试点项目(粤材教[2014]564号);广东省自然科学基金项目(2015A030310328)

孟佩佩(1982—)，女，山东荷泽，硕士，实验员，主要从事环境化学、环境监测等教学.

E-mail：ppmengjnu@163.com

S151.9;G642.0

B

1002-4956(2017)1-0062-07