直立挡土墙土压力研究

吴诗阳，李文轩

（南京水利科学研究院，江苏 南京 210024）

直立挡土墙土压力研究

吴诗阳，李文轩

（南京水利科学研究院，江苏 南京 210024）

基于库伦土压力墙后填土滑动楔体的极限平衡理论，建立滑动楔体上微元体的平衡方程，考虑水平力和竖向力的平衡条件，推导出适用于黏性土的主、被动土压力计算公式。该公式可以充分考虑滑裂面上黏聚力以及墙土间黏着力对土压力的影响，并且公式形式简单，易于计算。通过多个实例验算，计算结果与规范建议值和实测值相近，表明文中推导的公式合理可行，对工程具有一定的指导意义。最后分析了墙背摩擦角、墙土黏着力以及填土内摩擦角对挡土墙土压力的影响。

挡土墙；主动土压力；被动土压力；极限平衡；黏性土

0 引言

挡土墙土压力的计算一直是工程界和学术界关心的问题，如何准确计算出土压力是挡土墙设计的重点也是难点。从极限平衡理论出发，其典型代表是朗肯土压力理论和库伦土压力理论。但由于假设简单，二者的适用范围都有一定的局限性。其中朗肯土压力理论只适用于墙背垂直、光滑、墙后填土水平的情况；库伦土压力理论只适用于墙后填土为无黏性土的情况。但实际工程中很难严格满足其假设条件，这样会导致计算结果与实际值出现偏差。后来有不少学者[1-6]对库伦土压力理论进行修正和改进，使其能够适用于黏性土的计算。其中也有很多学者得出不错的结论，但计算公式异常复杂，很难运用到实际工程中去。

本文针对实际工程中较为常见的直立挡土墙，采用文献[7-9]的计算方法，沿深度方向取微分单元体进行分析，并在水平和竖直2个方向上建立力的平衡条件，从而推导出挡土墙上土压力分布、土压力合力及合力作用点的理论计算公式。并在此基础上推导出墙后填土为黏性土的主、被动土压力计算公式，以及墙后填土表面倾斜情况下的土压力计算公式。并且，在推导的过程中还可以考虑拉力区裂缝深度和墙土间黏着力对挡土墙土压力的影响。

1 土压力计算

1.1 主动土压力

库伦假设：假设挡土墙在填土压力作用下离开填土向前移动，当墙后土体达到极限平衡状态时（主动状态），土体中产生两个通过墙脚A的滑动面AC和AB，取滑动面AC与水平面夹角为θ。本文假设墙面垂直，填土水平，墙背与填土之间的摩擦角为δ，填土间的内摩擦角为φ。在沿深度y处取一微分单元，单元顶面作用压力Fy，单元底面作用反力Fy+dFy，单元左边作用水平力ex和剪力t1，右边作用法向力r和剪力t2，以及单元体自重dw。假设楔体式整体滑动，忽略单元上表面和下表面的剪力，如图1所示。

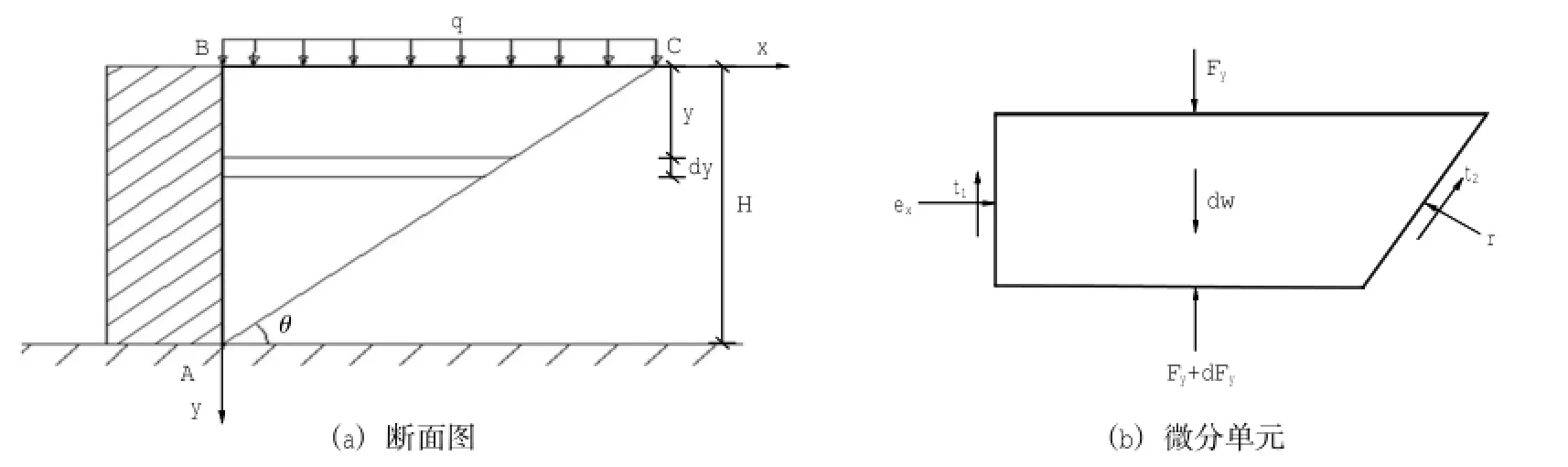
图1 墙后填土受力分析Fig.1 Stress analysis of the backfill behind the wall

考虑到滑裂面上黏聚力以及填土与墙背接触面上的黏着力，则t1=cw+extan δ，t2=c+rtan φ。

其中：cw即为墙背与填土间的黏着力，由于资料较少，采用文献[5]建议的方法，取cw=nc，n为0～1之间的系数，视影响因素确定；ex=KFy，K为侧压力系数。

根据力的平衡条件，取x方向平衡得：

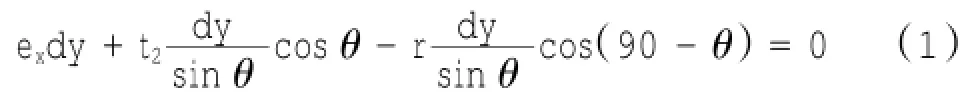
将t2代入并化简得：

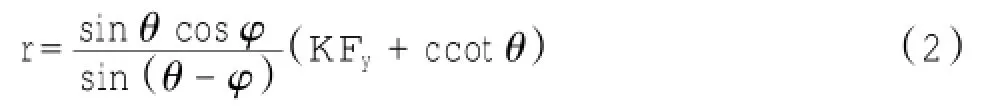
再取y方向平衡得：

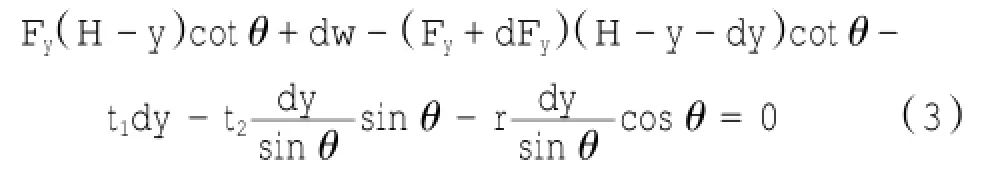
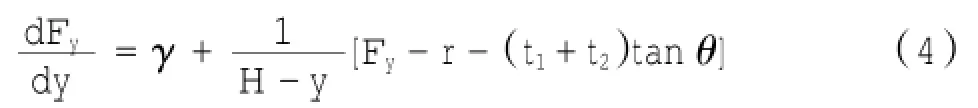
然后将t1、t2、r代入式（4）得：

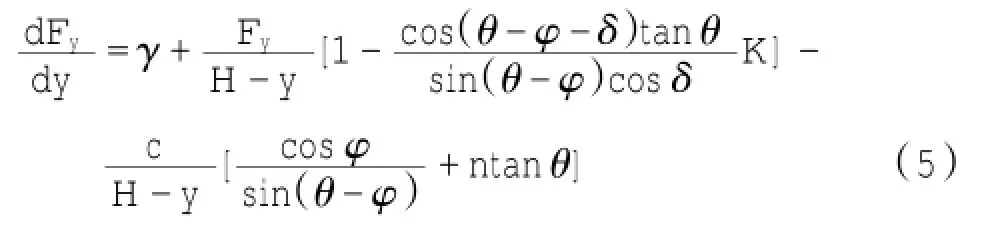
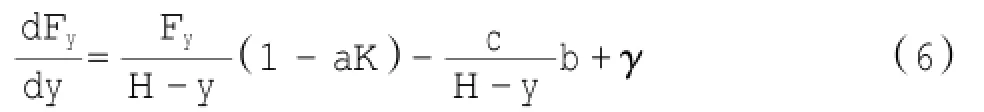
这就是墙后滑动楔块微元体的基本方程，通过求解式（6）便可得到竖向荷载的一般解，其解为：

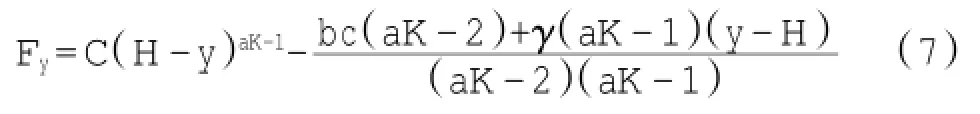
式中：C为常数，可以通过边界条件确定。本文当y=0时，Fy=q，代入式（7）得：

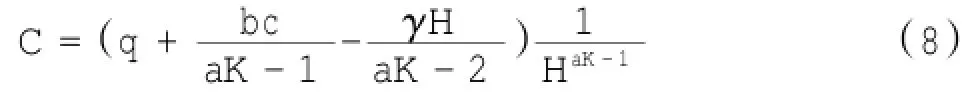
将式（8）代入式（7）得：

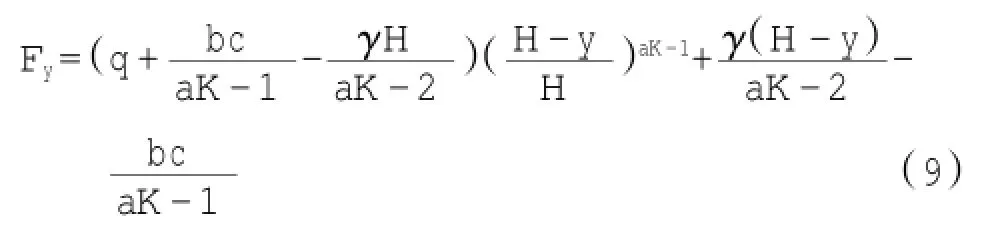
由上述可知ex=KFy，因此：

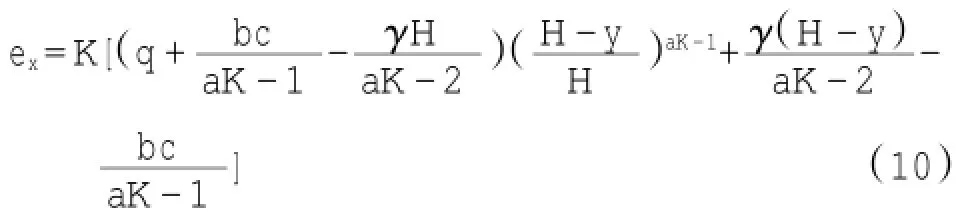
此式即为水平主动土压力的分布情况，可以看出ex的大小与H-y的aK-1次方相关，若aK-1=1时，ex呈线性分布，否则此分布呈非线性，这与近年许多学者得出的结果相似，更符合实际情况。

水平向的总土压力可以通过式（11）求得：

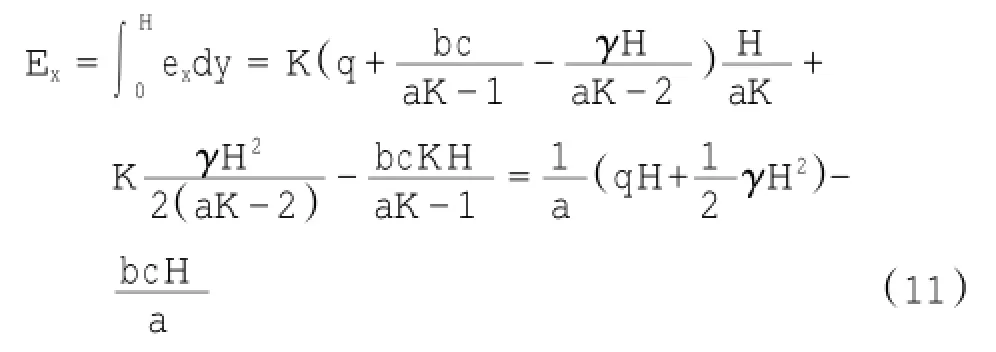
再将a，b代入得：

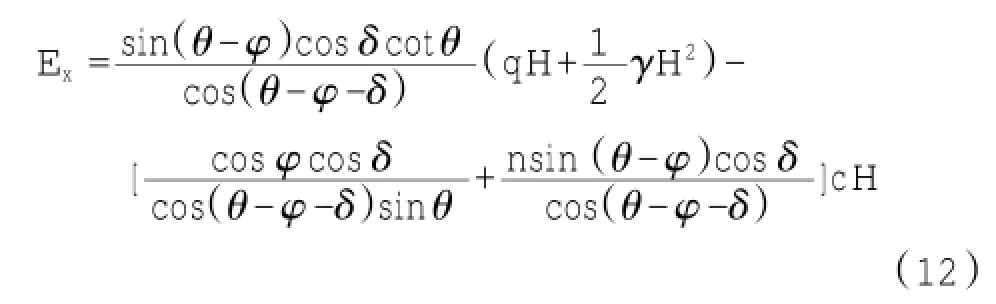
式（12）是水平土压力合力的一般计算公式，由于Ex=Ecos δ，因此：

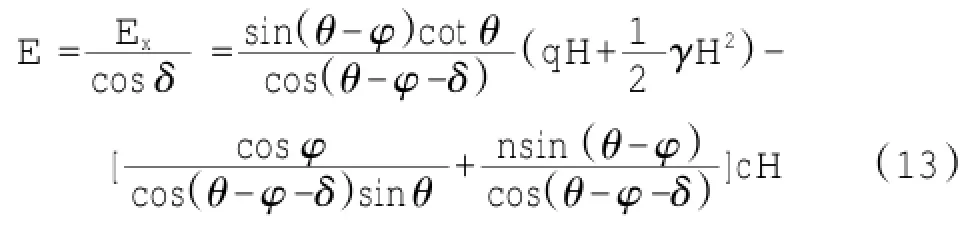
式（13）即为所求的总土压力的计算公式，当c=0时，公式（13）将化简成与文献[9]同样的公式，因此可以将文献[9]所推导的公式看成本文公式的一个特例。

从式（13）还可以看出，E是关于θ的函数，根据主动土压力的基本原理：“在所有可能的滑裂面倾角θ中，正好有一个导致最大土压力的倾角θcr”，即式（13）的最大值即为所求的主动土压力Ea，同时相对应的滑裂面倾角θcr。求解E可采用库伦土压力理论的方法，求dE/dθ=0时的θcr角，就可得到作用在墙背上的总库伦主动土压力的计算公式。但由于E的表达式有些复杂，推求的θcr角表达式有些繁琐和冗长，以至于求不出θcr的显式。因此本文通过c++软件编写相应的计算程序，通过试算法很容易求得式（13）的最大值，并能得到相应的θcr，同时精度也可以随意设定。

1.2 库伦公式对比

库伦公式的一般表达形式为：

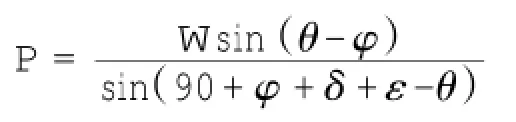
当ε=0，α=0时（墙背垂直，填土水平），可化为：

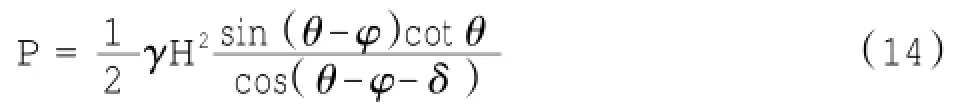
针对本文，当q=0，c=0时，式（13）可化为：

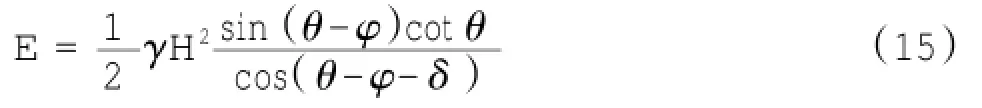
可见这两个公式完全相同，即在墙背垂直、填土表面水平情况下，库伦公式是本文公式的特例，下文还推导了填土表面倾斜情况下的土压力计算公式，扩充了本文计算公式的使用条件。

若考虑c的影响时，原有的库伦公式无从下手，而本文推导的公式可以很好地考虑黏聚力以及黏着力对土压力的影响，体现出优势性。但同时，也附带地引起了一个似是而非的问题[10-11]，即在计算主动土压力时，在挡土墙的顶部一定深度范围内，墙土之间将出现拉应力，很多学者都对其有过描述[12-14]，但对拉应力的理解各有不同。本文采用主流学说，认为这种拉应力是不可靠的，在计算过程中不考虑拉力的作用，并将拉应力区的土体，作为均载作用在土体上，即q′=γh0，Q= q+q′，其中h0即为地面裂缝深度，采用文献[6]建议的公式：

式中：Ka为朗肯主动土压力系数，当h0≤0时表示无裂缝开展，在计算中可令h0=0。若考虑这些影响，式（13）变为：

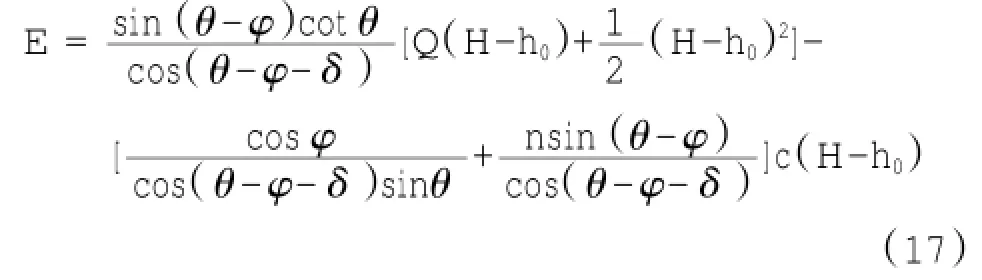
1.3 合力作用点位置

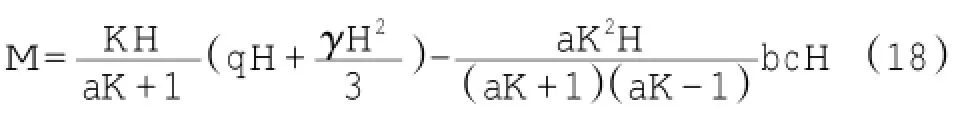
则合力作用点距墙角高度即为HA=M/Ex，得：

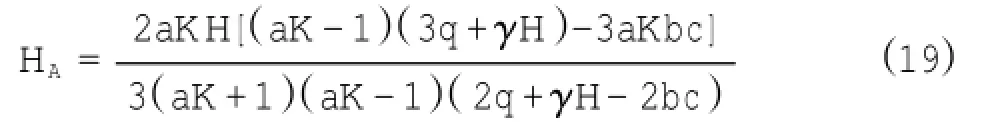
式中：K为侧压力系数，介于静止土压力系数与主动土压力系数之间，视具体情况而定。

1.4 被动土压力

采用与主动土压力类似的方法[15-21]，由于被动土压力作用方向的改变，则其水平和竖向平衡方程会发生相应的改变，受力分析见图2。

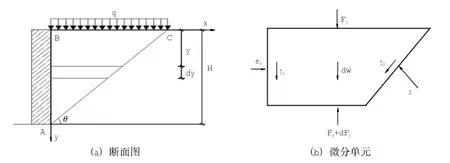
图2 被动土压力受力分析Fig.2 Stress analysis of passive earth pressure

水平方向和垂直方向平衡方程分别为：

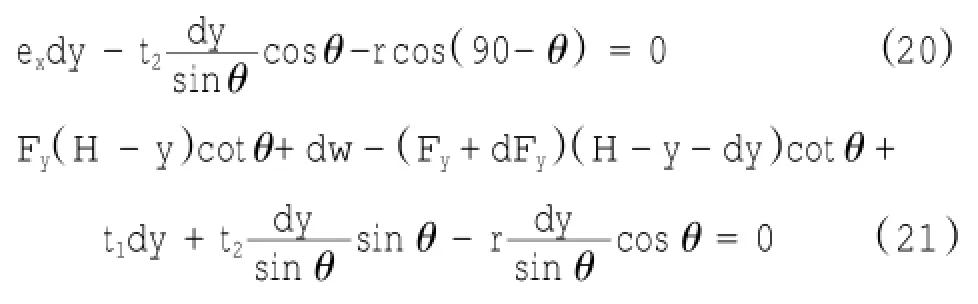
整理得：

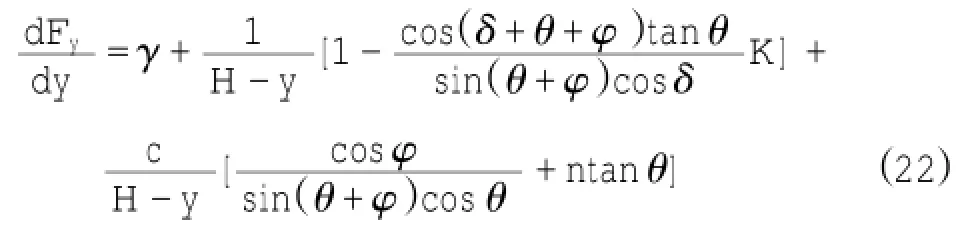
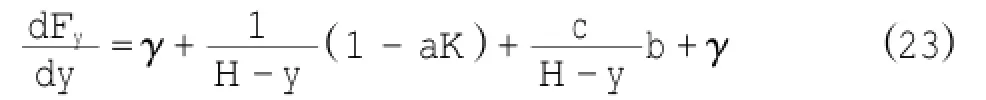
求解得：

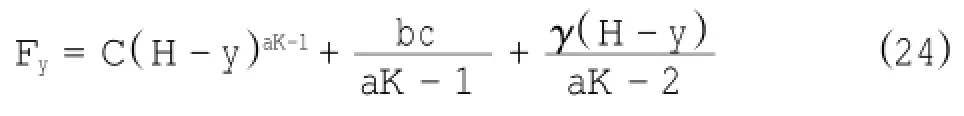
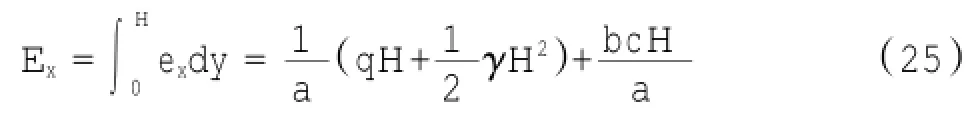
因此总库伦被动土压力的一般计算公式为：

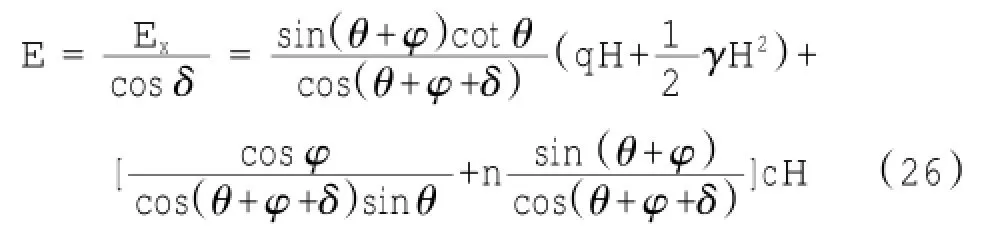
与上述一样，编写了计算程序，很容易求得其最小值，对比主动土压力公式和被动土压力公式不难发现，只需将主动土压力公式φ和δ角以及c变换为-φ，-δ和-c即可将主动土压力公式转换为被动土压力公式，非常方便。

1.5 墙后填土表面倾斜

考虑墙后填土倾斜的情况，即β≠0，由库伦理论可知，β≠0并不影响水平方向上力的平衡条件，故此可以将三角形ABC′的自重等效成m倍三角形ABC的自重，如图3所示。

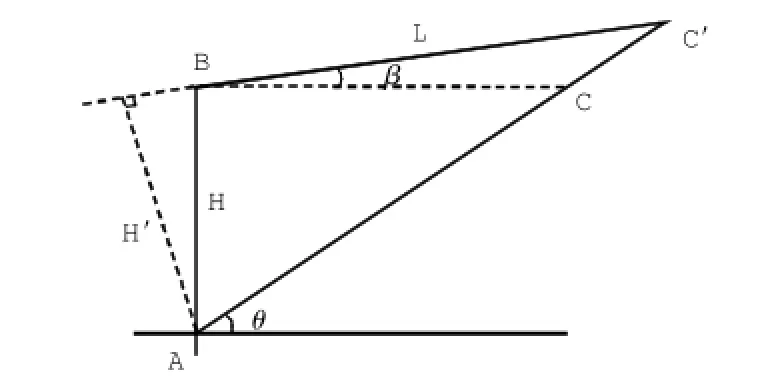
图3 墙后土体示意图Fig.3 Sketch of backfill behind the wall

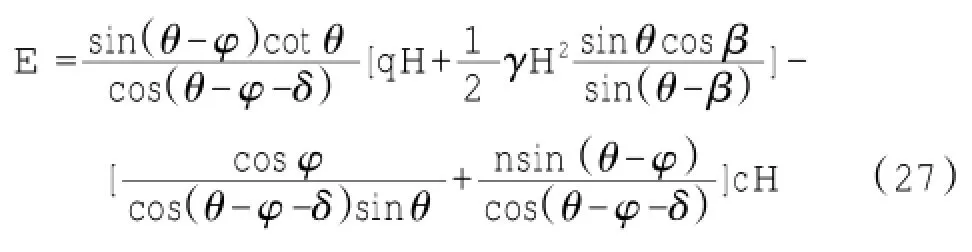
基于库伦土压力理论，式（13）、（26）、（27）即是在不同条件下的直立挡土墙土压力计算公式，公式形式比较简单，可以很好地通过简单的数值软件实现，便于在实际工程中使用。下文将验算本文推导公式的准确性。

2 算例分析

算例1：γ=18.6 kN/m3，H=10 m，φ=24°， q=0，α=0，β=0，cw=0，与文献[6]、规范对比如表1所示。

表1 主动土压力算例1Table 1 Example 1 of active earth pressure

从表1中可以看出，不管是黏聚力为0或不为0，通过本文的计算公式，都与规范公式接近，但本文推导的公式与文献[6]不同，数值却很接近，也间接反映本文推导公式的正确性，当c=0时，式（13）就转化为库伦土压力计算公式，但土压力的分布规律却与库伦土压力理论截然不同。

取文献[15]的数据H=4.45 m，γ=14.27 kN/m3，q=0，c=1.427 kPa，φ=24.26°，α=0，δ=21.4°，cw=0.98 kPa，测得刚性挡墙主动土压力强度分布如图4所示。取文献[21]的数据H=10 m，φ=30°，δ=10°，γ=18 kN/m3，c=0，α=0，β=0，可得被动极限状态下水平土压力分布如图5所示。

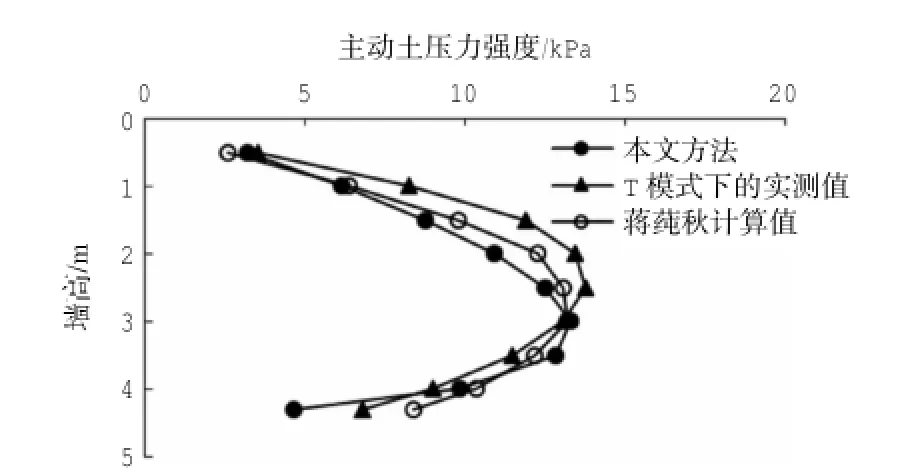
图4 主动土压力分布Fig.4 Distribution of active earth pressure

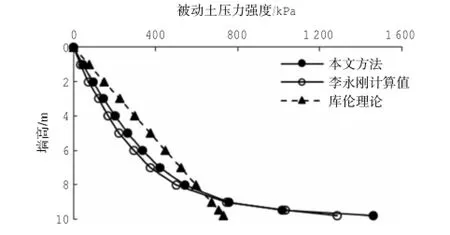
图5 被动土压力分布Fig.5 Distribution of passive earth pressure

从图4中可以看出主动土压力强度沿墙背为曲线分布，近似拱形，而非经典朗肯和库伦理论的线性分布，并与实测值和蒋莼秋计算值的分布情况基本保持一致，表明该分布的合理性。从图5中可以看出，与主动土压力强度分布不同，挡土墙上半部分的被动土压力强度缓慢增加，近似呈线性分布，下半部分则几乎呈指数增长，这是由于上部土体的约束，使下部土体接近三向受压状态，在墙体侧向挤压下所致[21]。而由库伦理论得出的土压力强度则呈线性分布，这与很多实际情况是相违背的。因此，不管是主动土压力强度分布还是被动土压力强度分布，都体现其非线性，更加接近实际情况。

算例2：H=4.6 m，γ=19.3 kN/m3，q=10 kN/m，φ=15°，α=0，δ=10°，β=0，c=10 kPa，cw=0，本文方法与其他学者的比较如表2所示。

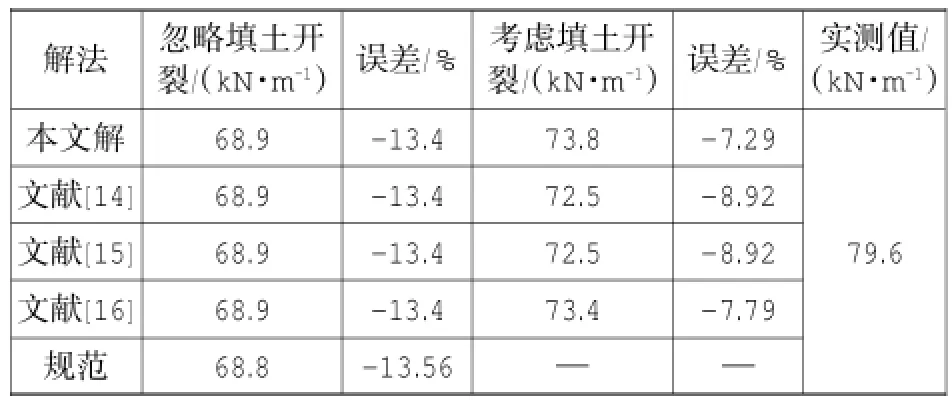
表2 主动土压力算例2Table 2 Example 2 of active earth pressure

当忽略填土开裂时，本文计算的结果和其他学者计算的结果相一致，但考虑填土开裂，也就是考虑黏性土拉力区的影响时，本文的结果更接近于实测值，表明本文推导的公式计算更加精确。

算例3：挡土墙高H=8.75 m，墙背倾角α= 0，填土重度γ=18 kN/m3，填土面倾角β=0，墙背摩擦角δ=13°，回填土与原状土间的黏聚力c= 12.2 kPa，墙背与填土的黏着力cw=8.2 kPa，摩擦角φ=18.8°，超载q=10 kN/m。与文献[17]和实测值进行了比较，其实测合力法向分力为170 kN/m，文献[17]计算的结果为161 kN/m，本文计算的结果是172.9 kN/m。

本文的计算结果与实测结果接近，所算的合力的相对误差为1.71%，文献[17]所算的误差为-5.3%。可见，本文推导的方法与实际更接近一些。本文所达到的精度，在工程中是可取的，说明了本文公式的可靠性。

算例4：取计算参数：q=0，α=0，β=0，φ=30°，δ=15°，cw=0。表3给出了被动土压力Ep/γh2随c/γh变化的计算结果并与文献[18]、[19]结果作比较。

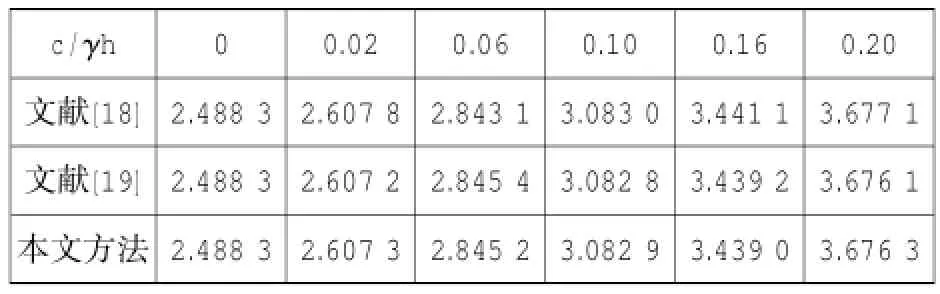
表3 被动土压力算例4Table 3 Example 4 of passive earth pressure

算例5：挡土墙高8 m，墙背倾角α=0，填土重度γ=16 kN/m3，填土面倾角β=0，填土间摩擦角φ=25°，墙背摩擦角δ=15°，q=10 kPa，c=10 kPa，cw=0，文献[20]计算所得被动土压力值为2 485 kN/m，本文方法为2 487.1 kN/m，两者较为接近。

从算例4和算例5中可以看出本文推导的被动土压力公式，计算结果与其他学者得到结果基本保持一致，但公式较为简单，便于实现。

3 考虑δ、φ、cw对挡土墙压力的影响

朗肯土压力理论假设墙面垂直光滑，即不考虑δ、cw对土压力的影响；库伦土压力理论虽然考虑了对挡土墙土压力的影响，但却无法考虑cw值的影响。本文通过式（13）考虑了这三者的影响，这里假设cw=nc，cw值通过n来表示。

3.1 δ和φ对土压力的影响

取γ=18 kN/m3，α=0，β=0°，H=8 m，q=10 kN/m，c=10 kPa，n=0.4。结果由图6、图7所示，从图6中可以看出，当δ值一定时，挡土墙上的主动土压力随着φ值的增大而减小，并呈非线性分布，减小的梯度随着φ值的增大而减小；从图7中可以看出当φ值一定时，土压力随着δ值的增大而减小，并基本呈线性分布；从图6中还可以看出，δ值对土压力的影响不是很大，当土的内摩擦角较大时，随着δ值的增加，土压力基本保持不变。因此若土的内摩擦角较大时（从图6中看出当φ≥30°）可以忽略δ值对土压力的影响，在简化计算时可以令其为0。

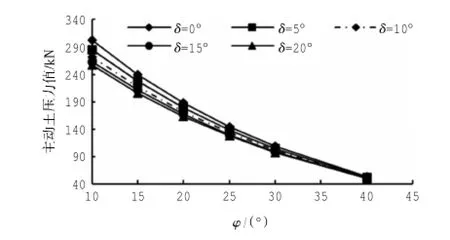
图6 土压力随φ值的变化Fig.6 Earth pressure changes with the value of φ

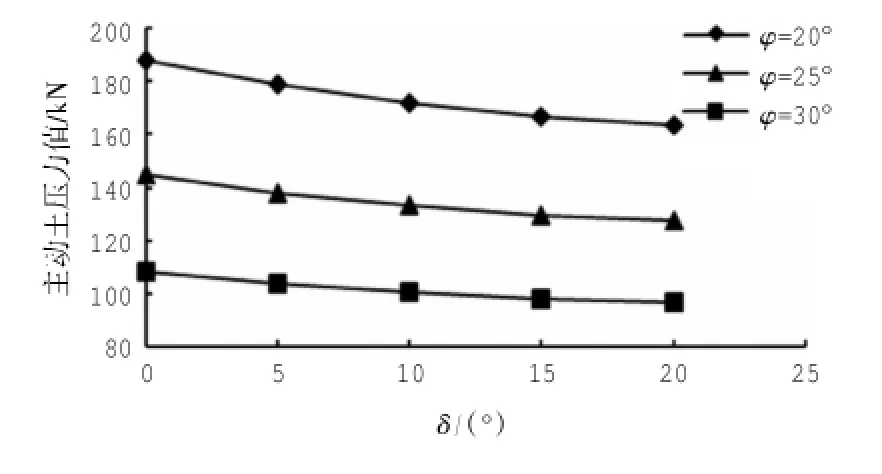
图7 土压力随δ值的变化Fig.7 Earth pressure changes with the value of δ

3.2 cw对土压力的影响

基本条件与上述一致，图8是在δ=10°下不同φ值和cw值对土压力的影响，图9是在φ=30°下不同δ值和cw值对土压力的影响。

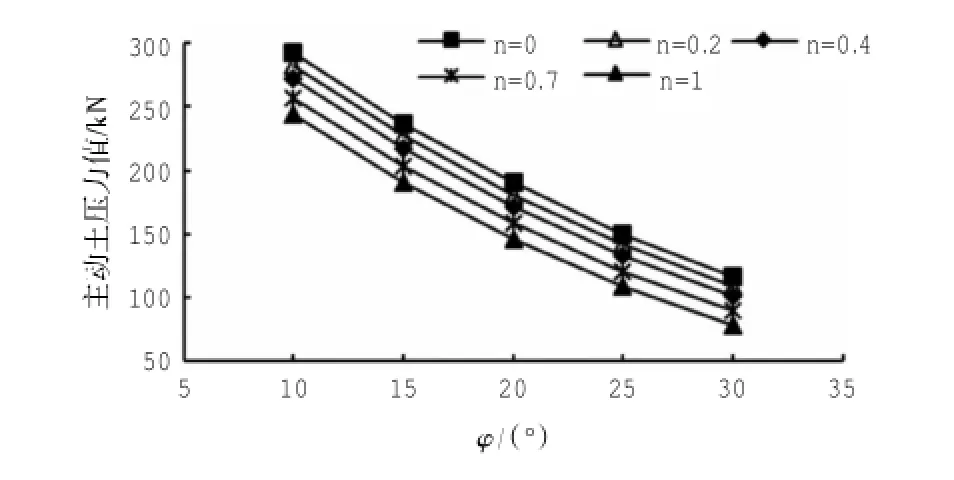
图8 不同φ值和cw值的土压力变化Fig.8 Earth pressure changes with different values of φ and cw

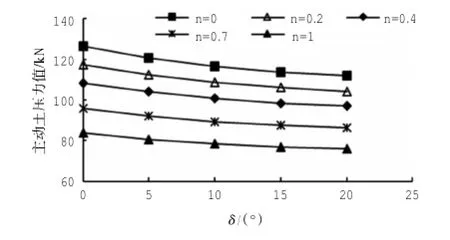
图9 不同δ值和cw值的土压力变化Fig.9 Earth pressure changes with different values of δ and cw

从图8、图9中可以看出，当φ值和δ值一定时，土压力随着cw值的增大而减小，其减小的梯度基本保持一直，即呈线性减小的趋势，对比图6，可见cw值对土压力的影响程度要大于δ值对土压力的影响。因此，朗肯土压力理论的假设会导致计算的主动土压力比实际值偏大，这在很多工程中得到证实，原因正是没有考虑cw值和δ值的影响。从图6～图9中可以看出，挡土墙上的主动土压力随着φ值、cw值、δ值的增大而减小，其影响程度是φ>cw>δ，因此在实际工程中，准确获取φ值和cw值尤为重要。

4 结语

本文基于库伦土压力计算理论，通过建立微元体的平衡方程，推导了直立挡土墙土压力的计算公式，其公式考虑了黏聚力以及黏着力的影响。通过多个实例验算，本文计算的结果较其他学者更为接近规范建议值和实测值，并且本文推导的公式形式简单，便于实现，易于在工程实际中推广使用。

同时还考虑了δ、φ、cw值对挡土墙土压力的影响。直立挡土墙上的主动土压力随着δ、φ、cw值的增大而减小；当墙后填土的内摩擦角较大时，则δ值对土压力的影响可以忽略，但cw值对土压力的影响在实际工程中是不容忽视的。

本文在前人的基础上推导了适用于黏性土计算的主、被动土压力公式，并首次考虑了cw值对挡土墙土压力的影响，公式形式简单，易于实现，计算结果较其他公式更加接近实测与规范建议值，但适用范围比规范大。

[1]李巨文，王翀，梁永朵，等.挡土墙后黏性填土的主动土压力计算[J].岩土工程学报，2006，28（5）：650-652. LI Ju-wen,WANG Chong,LIANG Yong-duo,et al.Computation of earth pressure of cohesive backfill on retaining wall[J].Chinese Journal of Geotechnical Engineering,2006,28(5):650-652.

[2]柯才桐，陈奕柏，高洪波，等.条形荷载下黏性土主动土压力计算[J].岩土力学，2013，34（S1）：167-172. KE Cai-tong,CHEN Yi-bo,GAO Hong-bo,et al.Calculation of active earth pressure for cohesive soil under action of strip surcharge[J].Rock and Soil Mechanics,2013,34(S1):167-172.

[3]胡晓军.黏性土主动土压力库伦精确解的改进[J].岩土工程学报，2006，28（8）：1 049-1 052. HU Xiao-jun.Improvement on Coulomb accurate solution of active earth pressure to cohesive soil[J].Chinese Journal of Geotechnical Engineering,2006,28(8):1 049-1 052.

[4]彭明祥.挡土墙主动土压力的库仑统一解[J].岩土力学，2009，30（2）：379-386. PENG Ming-xiang.Coulomb's unified solution of active earth pressure on retaining wall[J].Rock and Soil Mechanics,2009,30 (2):379-386.

[5]赵恒惠.挡土墙后黏性填土的土压力计算 [J].岩土工程学报，1983，5（1）：134-146. ZHAO Heng-hui.The computation of earth pressure of cohesive backfill on retaining wall[J].Chinese Journal of Geotechnical Engineering,1983,5(1):134-146.

[6]卢廷浩.考虑黏聚力及墙背黏着力的主动土压力公式[J].岩土力学，2002，23（4）：470-473. LU Ting-hao.A formula of active earth pressure including cohesion and adhesion[J].Rock and Soil Mechanics,2002,23(4):470-473.

[7]王元战，李新国，陈楠楠.挡土墙主动土压力分布与侧压力系数[J].岩土力学，2005，26（7）：1 019-1 022. WANG Yuan-zhan,LI Xing-guo,CHEN Nan-nan.Active earth pressure on a retaining wall and lateral coefficient of earth pressure [J].Rock and Soil Mechanics,2005,26(7):1 019-1 022.

[8]王元战，李蔚，黄长虹.墙体绕基础转动情况下挡土墙主动土压力分布[J].岩土工程学报，2003，25（2）：208-211. WANG Yuan-zhan,LI Wei,HUANG Chang-hong.Distribution of active earth pressure with wall movement of rotation about base[J]. ChineseJournal of Geotechnical Engineering,2003,25(2):208-211.

[9]WANG Y Z.Distribution of earth pressure on a retaining wall[J]. Geotechnique,2000,50(1):83-88.

[10]魏汝龙.库仑土压力理论中的若干问题[J].港工技术，1999（2）：31-38. WEI Ru-long.Some problems in Coulomb′s theory of earth pressure[J].Port Engineering Technology,1999(2):31-38.

[11]WEI Ru-long.Application of Coulomb′s theory to cohesive soil[J]. Chinese Journal of Geotechnical Engineering,1998,20(3):80-84.

[12]陈庆，刘小丽，曹勉励.黏性土主动土压力计算方法研究[J].地下空间与工程学报，2015，11（5）：1 180-1 184. CHEN Qing,LIU Xiao-li,CAO Mian-li.On the computation methods of active earth pressure of cohesive soil[J].Chinese Journal of Underground Space and Engineering,2015,11(5):1 180-1 184.

[13]陈文胜，赵勤彦，凌同华.经典朗肯土压力墙后土体滑裂面机制研究[J].岩土力学，2011，32（12）：3 571-3 576. CHEN Wen-sheng,ZHAO Qin-yan,LING Tong-hua.Sliding surface mechanism of limit soil mass under classical Rankine earth pressure[J].Rock and Soil Mechanics,2011,32(12):3 571-3 576.

[14]顾慰慈.黏性土主动土压力的计算[J].水利学报，1991（2）：55-64. GU Wei-ci.Calculation of active earth pressure for cohesive soil[J]. Journal of Hydraulic Engineering,1991(2):55-64.

[15]柯才桐，陈奕柏，朱嘉.挡土墙土压力线性分布解[J].岩石力学与工程学报，2014，33（S1）：3 312-3 317. KE Cai-tong,CHEN Yi-bo,ZHU Jia.A linear distribution solution of earth pressure on retaining wall[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):3 312-3 317.

[16]杨敏，刘斌，周建武.挡土墙主动和被动土压力的统一解[J].同济大学学报：自然科学版，2011，39（2）：187-193. YANG Min,LIU Bin,ZHOU Jian-wu.Unified solution of active and passive earth pressure on retaining wall[J].Journal of Tongji University:Natural Science,2011,39(2):187-193.

[17]林智勇，戴自航，苏美选.复杂条件下挡土墙主动土压力解析解[J].岩土工程学报，2008，30（4）：555. LIN Zhi-yong,DAI Zi-hang,SU Mei-xuan.Analytical solution of active earth pressure action on retaining walls under complicated conditions[J].Chinese Journal of Geotechnical Engineering,2008, 30(4):555.

[18]李兴高，刘维宁.被动土压力作用的变分极限平衡法研究[J].工程力学，2007，24（1）：11-17. LI Xing-gao,LIU Wei-ning.Study on the passive earth pressure by variational limit equilibrium method[J].Engineering Mechanics, 2007,24(1):11-17.

[19]马崇武.黏性土挡土墙被动土压力的计算[J].兰州理工大学学报，2016，42（1）：124-127. MA Chong-wu.Evaluation of passive earth pressure on retaining walls with cohesive soil backfill[J].Journal of Lanzhou University of Technology,2016,42(1):124-127.

[20]林宇亮，杨果林，黄向京.挡墙后黏性土被动土压力的薄层微元法[J].公路交通科技，2011，28（3）：12-19. LIN Yu-liang,YANG Guo-lin,HUANG Xiang-jing.Thin-layer micro-element method for computing passive earth pressure of backfilled cohesive soil on retaining wall[J].Journal of Highway and Transportation Research and Development,2011,28(3):12-19.

[21]李永刚.挡土墙被动土压力研究[J].岩土力学，2003，24（2）：273-276. LI Yong-gang.Study on passive earth pressure of retaining wall[J]. Rock and Soil Mechanics,2003,24(2):273-276.

Study on earth pressure of vertical retaining wall

WU Shi-yang,LI Wen-xuan
（Nanjing Hydraulic Research Institute,Nanjing,Jiangsu 210024,China）

Based on Coulomb′s soil pressure of limit equilibrium theory of backfill sliding wedge,we established the balance equation of the sliding wedge element,and considered the equilibrium condition of horizontal force and vertical force,then derived the active and passive earth pressure formula which is suitable for cohesive soils,and the formula can reflect the effect of the soil cohesion on the sliding surface and adhesion between soil and retaining wall on the soil pressure,also the formula is very simple and easy to calculate.Through some examples'calculation,the results of calculation are similar to the standard values and the measured values.These show that the formula is reasonable and feasible,and it has a guiding significance to the project.Finally,we analyzed the effect of the wall friction angle,soil wall adhesion and the internal friction angle on earth pressure of retaining wall.

retaining wall;active earth pressure;passive earth pressure;limit equilibrium;cohesive soil

U655.54；TU432

A

2095-7874（2017）01-0012-07

10.7640/zggwjs201701003

2016-07-08

2016-09-06

江苏省科技支撑计划项目（BE2013663）；南京水利科学研究院重点基金项目（Y315010）

吴诗阳（1990— ），男，安徽青阳人，博士研究生，岩土工程专业，主要从事结构与土的相互作用和土工合成材料研究。E-mail：718228381@qq.com