基于方差分量估计的不同截止高度角下的组合单点定位

冯 彪，柴洪洲，王 敏，潘宗鹏，李 迪

(信息工程大学，河南 郑州 450000)

基于方差分量估计的不同截止高度角下的组合单点定位

冯 彪，柴洪洲，王 敏，潘宗鹏，李 迪

(信息工程大学，河南 郑州 450000)

BDS/GPS/GLONASS组合系统定位时，由于系统间卫星测距精度的差异性，需要合理确定卫星间权比，Helmert方差分量估计常被用于确定不同类观测值间权比；而当观测值含有粗差时，Helmert方差分量估计定位结果容易被粗差污染或收敛失真，出现大的偏差。文中基于Helmert方差分量估计，引入等价权因子IGGIII函数，建立抗差Helmert方差分量估计权函数模型，对比分析其在低截止高度角10°、15°和20°下，在BDS/GPS/GLONASS组合系统定位中的应用及定位精度，并讨论分析在高截止高度角30°和40°下，组合系统和单系统BDS的定位精度。实验结果表明：当观测值无明显粗差时，Helmert方差分量估计和抗差分量估计的定位精度相当，略低于高度角权函数的定位结果，点位精度RMS优于2.5 m；含粗差时，抗差解定位精度最高；当截止高度角为30°时，BDS单系统定位精度RMS优于5 m，而组合系统RMS接近3 m；为40°时，组合系统平面精度RMS优于2 m，三维精度RMS优于6 m，而单系统不能定位。

BDS/GPS/GLONASS组合系统定位；截止高度角；Helmert方差分量估计；IGGIII等价权函数；抗差估计；定位精度

北斗卫星导航系统(BDS)于2012年正式向我国及周边地区提供区域服务，预示着全球卫星导航系统(GNSS)进入多系统兼容、合作的发展时代。单一系统往往由于用户位置和观测条件受限，不能提供足够的卫星数以获取较高精度的位置信息，满足不了用户需求，多系统联合导航定位逐渐成为GNSS发展研究的热点。但由于各卫星导航系统星座和卫星轨道分布不同，卫星的测距精度存在差异以及系统的定位能力的差别，GNSS联合定位时，再根据先验精度确定观测值间权比不再准确可靠。因此，对于组合导航系统，各导航系统间和卫星间的权重因子优化和其导航定位性能是研究多系统组合导航定位的重要方面。

1942年，一种验后方差估计的方法被提出，即Helmert方差分量估计。它是通过迭代计算自适应的调整不同类或不等精度观测值之间的权比，使权的分配更具合理性[1-2]。但由于基于最小二乘的方差分量估计不具有抗差性，若观测值含有粗差，粗差会污染随机模型，导致迭代收敛失真或不收敛，定位结果也偏离真值[3-4]。为了减弱粗差对Helmert方差分量估计结果的影响，可以应用抗差Helmert方差分量估计的方法来合理调整3类观测值之间的权比，降低粗差观测值的权，削弱其对定位结果的影响[5-6]。关于组合系统的导航定位性能[7-11]，相关的分析比较都是在低截止高度角下10°或15°的，相对单系统BDS和GLONASS，其导航定位性能提升明显，而GPS不明显。但对于截止高度角较大的情况，如城市、峡谷地区等的应用，组合系统的导航定位性能及与单系统的差别分析较少，特别对正处于建设中的北斗系统，目前的应用能否满足上述条件的导航定位服务。因而，本文主要研究分析基于方差分量估计的BDS/GPS/GLONASS组合系统在低截止高度角10°、15°和20°下，3种不同权函数的定位精度和抵御粗差的能力以及探讨在高截止高度角30°和40°下，组合系统和单系统BDS的导航定位性能。

1 BDS/GPS/GLONASS组合系统理论

1.1 时空基准统一

GPS、BDS、GLONASS 3个导航系统都是采用独立的时间和坐标系统。GPS采用GPS时GPST，起算历元为协调世界时UTC的1980年1月6日0时；BDS采用北斗时BDT，起算历元为UTC的2006年1月1日0时。GPST和BDT都是以原子时为时间基准，是一个连续的时间系统，不存在跳秒。但由于闰秒和两个维持时间系统维持的差异，GPST与BDT存在整14 s和微小同步误差。GLONASS采用GLONASS时GLONASST，GLONASST是采用莫斯科地区的协调世界时UTC，与协调世界时UTC时存在3 h偏差。GLONASST也存在跳秒，且与UTC保持一致。

GPS采用WGS84坐标系统，BDS采用CGCS2000坐标系统，二者定义一致，仅框架实现有差异，同一点在两个坐标系统下的坐标差异在cm级[12]。GLONASS采用PZ-90.02，与ITRF2000只存在原点的平移，3个轴的定向一致，两坐标系偏差维持在1～2 dm内[13]。因此，鉴于伪距定位的精度低于cm级，组合系统单点定位不需进行坐标转换。

1.2 观测方程

GPS、GLONASS和BDS组合单点定位的观测方程为

2 组合系统观测值随机函数模型

2.1 Helmert方差分量估计

将各卫星系统伪距观测值分为3类观测值，根据Helmert方差分量估计原理，其计算过程[14]如下：

1)第一次最小二乘平差时，GPS、GLONASS、BDS观测值根据卫星高度角先验定权P1，P2，P3，先验权比为

(2)式中，eli为卫星i的高度角。

3)按下式进行方差分量估计

(3)式中:

N=ATPA=A1TP1A1+A2TP2A2+A3TP3A3=N1+N2+N3.

(4)

其中:n1为GPS观测值的个数,n2为GLONASS观测值的个数，n3为BDS观测值的个数。

4)重新定权

(5)

针对上述过程中易出现迭代不收敛或收敛失真现象，分析原因一是可能在于各类观测值的个数不均衡，如果一类观测值个数太少，Helmert方差分量估计确定的权比就易失真；二是在观测数据预处理过程中，如果各类观测值残差相差太大，迭代过程可能就出现不收敛或迭代次数太多，S矩阵就为奇异阵，无法定位解算。因此，解算过程中需注意历元中各类卫星数，以决定是否采用Helmert方差分量估计；在遇到迭代过程发散，需再对各卫星残差进行分析，重新筛选卫星或适当降低一些卫星的权重，如抗差，再进行解算。

2.2 基于IGGIII的抗差Helmert方差分量估计

由最小二乘原理知，当观测值中含有粗差时，观测值的残差易受粗差的影响，从而导致Helmert方差分量估计出现震荡现象，迭代结果失真[15]。为了避免粗差对Helmert方差分量估计结果的影响，可以采用等价权的方法对含有粗差的数据降权处理[2]。在BDS、GPS、GLONASS组合定位中，系统间观测值相互独立，相应的等价权为

(6)

式中:Pi为原始权阵，wi为自适应权因子，采用IGGⅢ函数[16]，如下式：

(7)

式中：k1，k2为常数，一般取k1=1.5～2.0，k2=3.0～8.0。结合Helmert方差分量估计，抗差Helmert方差分量估计的主要步骤是在步骤3)后，引入等价权因子重新定权，再进行方差分量估计。

3 实验分析

实验数据采用MGEX nnor站2015年12月12日24 h的观测数据，采样率为30 s，共计2 880个历元。定位结果精度分析采用将各历元解算的坐标与IGS发布的测站参考真值间的偏差转换为站心之间坐标E、N、U 3个方向，分别统计3个方向分量的内外符合精度STD和RMS。为了对比分析抗差Helmert方差分量估计、Helmert方差分量估计以及常规高度角定权3种权函数模型对BDS/GPS/GLONASS组合系统定位精度的影响和抵御粗差的能力以及组合系统的导航定位精度，进行以下两种方案实验：

方案1：截止高度角为10°、15°和20°时，3种不同权函数下，组合系统的导航定位精度分析；

方案2：截止高度角为30°和40°时，组合系统和单系统BDS的定位精度分析。

实验方案1中，卫星截止高度角为10°的定位解算结果如图1～图7所示。图1、图2分别为GPS、BDS单系统定位结算结果；图3、图4分别为GPS/BDS组合定位Helmert方差解和抗差解；图5、图6、图7分别为BDS/GPS/GLONASS组合定位3种权函数模型的定位结果。

在截止高度角为10°下，不同卫星系统和权函数模型的定位结果统计如表1所示，统计历元数都大于2 800，接近总历元数。

从图1～图7和表1可知，GPS定位精度优于BDS，两系统定位结果在U方向表现一致，都存在周期性波动，GPS更显著；而在E、N方向，BDS变化曲线稳定性明显差于GPS。组合系统定位精度相对GPS单系统提升较少，15%左右，而对BDS提升约40%，显著提高。但在E方向上，组合系统定位精度低于GPS单系统，N方向上提升也较小，U方向上改善显著，说明卫星数增加对提高GPS单系统U方向精度作用最大。组合系统BDS/GPS/GLONASS相对BDS/GPS的定位结果，两者定位精度相当，可能在于观测到的GLONASS卫星数较少，BDS/GPS组合定位精度已较高，卫星数再增加对精度提升作用较小。组合系统BDS/GPS或BDS/GPS/GLONASS，抗差Helmert方差分量估计定位解与Helmert方差分量估计定位解精度一样，稍差于高度角权函数模型，可能因为测站观测数据质量较好，无明显粗差，反而方差分量估计迭代过程中，不同系统间卫星数差异和各卫星后验残差相差较大，致确定的系统间权比出现大的偏差，因而迭代解算结果更差，如图中的“尖刺”点。也说明当多余观测数不充足时或组合系统中某个系统可见星较少时，采用Helmert方差分量估计调整系统间权比不再适用。

图1 GPS单系统定位结果在E、N、U方向的坐标差值

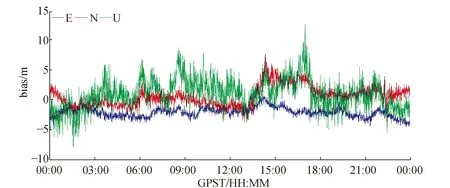
图2 BDS单系统定位结果在E、N、U方向的坐标差值

图3 BDS/GPS组合定位Helmert方差解在E、N、U方向的坐标差值

图4 BDS/GPS组合定位抗差解在E、N、U方向的坐标差值

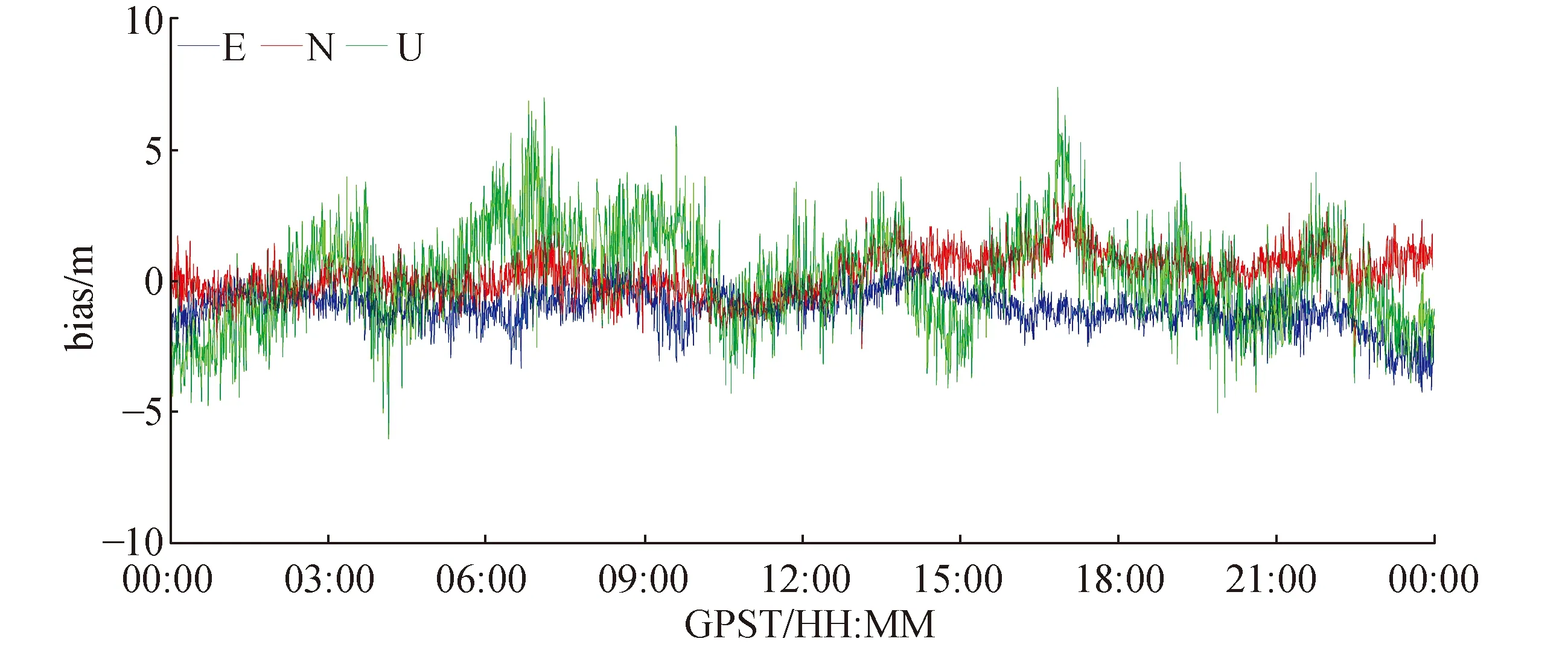
图5 BDS/GPS/GLONASS组合高度角定权函数模型定位解算结果

图6 BDS/GPS/GLONASS组合Helmert方差分量估计权函数模型定位解算结果

图7 BDS/GPS/GLONASS组合抗差分量估计权函数模型定位解算结果

表1 不同卫星系统定位结果 m

方案1中，卫星截止高度角为15°和20°时，不同模型定位结果统计如表2、表3所示。

表2 15°下不同模型定位结果统计 m

表3 20°下不同模型定位结果统计 m

从表1～表3的统计结果可知，随卫星截止高度角增大，导航系统定位精度逐渐降低。对GPS单系统，定位精度下降趋势明显，主要是卫星数减少。而BDS，10°和15°情况下，系统定位精度及N、E、U 3方向上差异很小，20°时定位精度下降较低，体现了BDS异构星座的特点。两系统都呈现出在E、N方向上，定位精度受卫星数变化的影响小于U方向。同样，对于3种权函数模型，高度角权函数模型定位精度最高，Helmert方差分量估计和抗差分量估计对提高定位精度的作用不是很显著。组合系统BDS/GPS和BDS/GPS/GLONASS定位精度都优于3 m，精度相当；相对单系统，精度都有显著提高。

针对上述试验中3种权函数定位结果精度相当，Helmert方差分量估计和抗差分量估计对提升定位精度的作用并不明显的问题，分析原因可能主要在于实验中采用的nnor站观测数据质量较好。而在实际观测过程中，因为观测条件和仪器的差异，GNSS观测数据质量可能会稍差，含部分粗差。因此，为进一步分析高度角权函数、Helmert方差分量估计和抗差分量估计抵御粗差的能力，在原始观测数据中随机加入10～20 m不等的偏差，3种权函数的定位结果如图8～图10所示。

图8 含粗差下BDS/GPS/GLONASS组合高度角定权函数模型定位解算结果

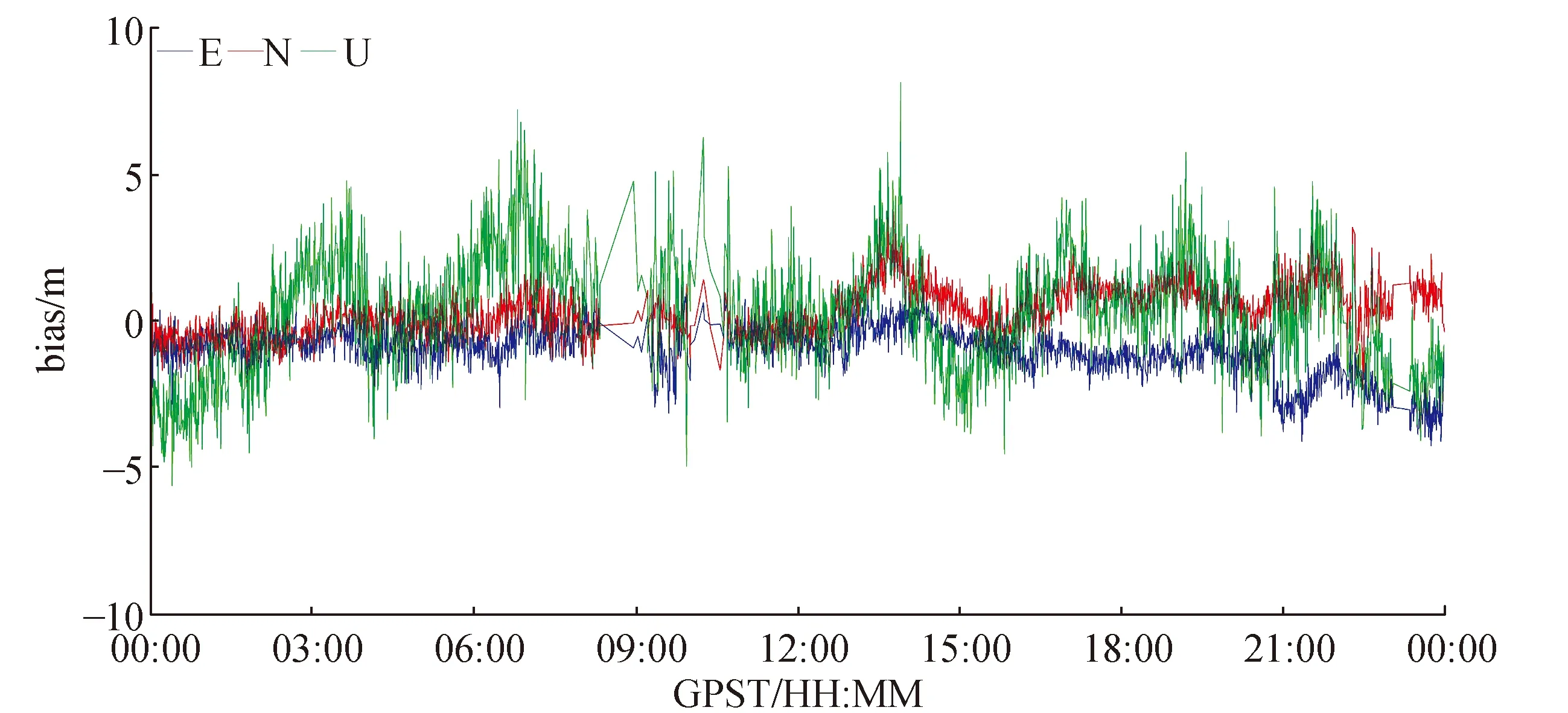
图9 含粗差下BDS/GPS/GLONASS组合Helmert方差分量估计权函数模型定位解算结果

图10 含粗差下BDS/GPS/GLONASS组合抗差分量估计权函数模型定位解算结果

从图8～图10中明显可以看出，在观测值含粗差时，高度角权函数定位结果受粗差影响较大，发生了大的偏差；Helmert方差分量估计定位结果也同样受到粗差的影响，定位解算过程中方差分量估计迭代失真和迭代过程不收敛，无法定位，即图9中“尖刺”点和折线连接部分；而抗差分量估计能较好抵御粗差的影响，改善粗差对定位结果的“污染”，提高定位精度。

针对组合导航系统卫星数成倍增加和更优的卫星空间几何构型的特点，进一步探讨分析其在截止高度角较大的情况下的导航定位性能，即实验方案2。图11为组合系统和单系统在卫星截止高度角为30°时的可视卫星数，图12～图16分别为GPS、BDS、GLONASS 3种系统不同组合模式在高度角权函数下，各系统的定位结果在E、N、U 3方向的坐标差值。30°不同模型定位结果统计见表4。

从图11可知，在高度截止角为30°时，BDS单系统整天内可见卫星数都大于5颗，为6～10颗，相对GPS、GLONASS可观测时间更长，说明BDS星座分布更具优势。组合系统相对任一单系统可见卫星数更多，G/R/C可见卫星数最多，绝大部分观测时段可见卫星数大于15颗；G/C可见卫星数在13颗左右，C/R为11颗左右；G/R最少，可见卫星数与观测时段有关，变化较大。

图11 导航系统的可见卫星数

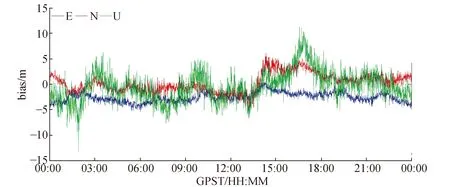
图12 BDS定位结果

图13 BDS/GPS组合系统定位结果

图14 GPS/GLONASS组合系统定位结果

图15 BDS/GLONASS组合系统定位结果

图16 BDS/GPS/GLONASS组合系统定位结果

表4 30°不同模型定位结果统计 m

从图12～图16和表4可以看出，在卫星高度截止角较大的情况下，组合系统相对单系统的导航定位优势更明显。单系统GPS和GLONASS由于可见卫星数不足或可观测时间较短，不能提供导航定位服务，而组合系统全天都能用于导航定位。特别，BDS单系统整天可视卫星数也能满足定位，定位精度也相对较高，为4.459 m，与BDS/GLONASS精度相当。组合系统BDS/GPS/GLONASS定位精度最高，点位精度为3.098 m；BDS/GPS组合定位精度优于GPS/GLONASS和BDS/GLONASS，为3.220 m；BDS/GLONASS组合定位精度为4.311 m，与BDS单系统相差无几；GPS/GLONASS组合系统由于卫星数较少，且不稳定，定位精度最差。

随着卫星截止高度角升高，组合系统可见星也逐渐减少。在截止高度角为40°时，单系统BDS和GPS/GLONASS、BDS/GLONASS组合系统大部分时段可观测卫星数较少，不能定位或精度太差；而BDS/GPS和BDS/GPS/GLONASS组合系统整天可见星数依旧大于6颗，为7～14颗，其定位结果如图17、图18所示。40°不同模型定位结果统计见表5。

从图中可以看出，组合系统定位结果在E、N方向上较稳定，平面位置精度仍相对较高，在3 m以内；而U方向上波动较大，绝大部分观测时段在-10～+10 m内波动，个别时刻达到20 m左右；BDS/GPS/GLONASS组合系统相对BDS/GPS系统，增加的卫星数对改善U方向的精度作用很小，甚至可能降低，如图中10～11点间所示。

图17 BDS/GPS组合系统定位结果

图18 BDS/GPS/GLONASS组合定位结果

表5 40°不同模型定位结果统计 m

从表5可知，在高度截止角为40°时，BDS/GPS组合定位精度为5.821 m，平面定位精度优于3 m，高程精度稍差，为5.474 m；BDS/GPS/GLONASS组合系统定位精度为5.864 m，平面定位精度与BDS/GPS一样，高程精度略差于BDS/GPS，两者导航精度都小于6 m。这也充分说明组合系统的导航定位优势，在高截止卫星高度角下，如城市、山区和峡谷地区等，可见星数仍足够定位，且导航定位精度较高，也能连续提供服务。

4 结 论

本文针对BDS/GPS/GLONASS组合系统联合定位时，不同权函数模型——高度角定权、Helmert方差分量估计和抗差分量估计的定位精度和组合导航系统及单系统BDS导航定位性能进行分析，并探讨了3种权函数对粗差的抵御能力。实验结果表明，当观测值含有粗差时，抗差分量估计定位结果最好。

在低截止卫星高度角下，BDS/GPS/GLONASS组合系统定位精度与BDS/GPS相当，较GPS单系统定位精度提升15%，BDS提升40%，随卫星截止高度角增大，GPS精度提升增大到23%，而BDS不变；特别，当卫星截止高度角为30°时，GPS单系统可见卫星数低于4颗，不能定位；而BDS系统由于其异构星座分布的特点，可视卫星数为6～9颗，其导航定位精度优于5 m；且随着我国北斗的建设，卫星数将不断增多，其城市高截止高度角地区的应用将不再是问题。

BDS/GPS/GLONASS组合系统在城市或峡谷地区的应用，即当卫星截止高度角较大时，等于30°或40°，组合系统相对单系统的导航定位优势更为突出，单系统往往不能定位或导航定位服务不连续，而组合系统能提供连续的导航定位，且精度优于6 m。

上述结论仅只是相对于中国区域或周边部分地区。

[1] GRAFAREND E.W,Schaffrin B.Variance-Covariance-Component Estimation of Helmet Type[J],Surveying and Mapping,1979.No.1.

[2] CAI C,GAO L P Y.A Precise Weighting Approach with Application to Combined L1/B1 GPS/BeiDou Positioning[J].Journal of Navigation,2014,67(5):911-925.

[3] 刘长建，马高峰.抗差Helmert方差分量估计及其应用[J].北京测绘，2002(1)：16-18.

[4] 秦显平，杨元喜.抗差方差分量估计在卫星定轨中的应用[J].大地测量与地球动力学，2003,23(4)：40-43.

[5] 高晓,戴吾蛟.抗差Helmert方差分量估计在GPS/BDS组合定位中的应用[J].大地测量与地球动力学,2014,34(1):173-176.

[6] 张勇,田林亚,徐君民,等.抗差方差分量估计在GPS/GLONASS组合导航中的应用[J].测绘科学技术学报,2013,30(2):132-135.

[7] 李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模融合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.

[8] 何俊,袁小玲,曾琪,等.GPS/BDS/GLONASS组合单点定位研究[J].测绘科学,2014,39(8):124-128.

[9] 徐龙威,刘晖,张明,等.不同截止高度角多模GNSS组合单点定位性能分析[J].大地测量与地球动力学,2015(6):987-991.

[10] SANTERRE R,PAN L,CAI C,et al.Single Point Positioning Using GPS,GLONASS and BeiDou Satellites[J].Positioning,2014,5(4):107-114.

[11] MAN X,SUN F,LIU S,et al.Analysis of Positioning Performance on Combined BDS/GPS/GLONASS[M].China Satellite Navigation Conference (CSNC) 2015 Proceedings: Volume II.Springer Berlin Heidelberg,2015:399-409.

[12] 程鹏飞,文汉江,成英燕,等.2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J].测绘学报,2009,38(3):189-194.

[13] 郭际明,孟祥广,李宗华,等.GLONASS卫星广播星历精度分析[J].大地测量与地球动力学,2011,31(1):68-71.

[14] 刘长建,马高峰.Helmert方差分量估计的粗差检验与抗差解[J].测绘信息与工程,2002,27(6):5-7.

[15] 黄维彬.近代平差理论及其应用[M].北京：解放军出版社，1992.

[16] 杨元喜.自适应动态导航定位 [M].北京：测绘出版社，2006.

[责任编辑：刘文霞]

Combined single point positioning with different cut-off elevation angle using variance component estimation

FENG Biao, CHAI Hongzhou, WAN Min, PAN Zongpeng, LI Di

(Information Engineering University, Zhengzhou 450000, China)

When the combination of BDS/GPS/GLONASS system is positioned, due to the difference of the accuracy of satellite ranging between systems, a reasonable determination of weight ratio between satellites is needed.Helmert variance component estimation is often used to determine weight ratio of different observations. However, when the observations contain gross errors, the positioning results of Helmert variance component estimation are easy to be contaminated by gross errors or convergence distortion. This paper, based on Helmert variance component estimation, introduces the equivalent weight factor IGGIII function, to establish weight function model of robust Helmert variance component estimation, comparing and analyzing its application and positioning accuracy in combined of BDS/GPS/GLONASS system positioning under low cut-off angles of 10°, 15° and 20°. Then it discusses and analyzes the combination system and BDS positioning accuracy with the high cut-off elevation angle of 30°and 40°. Experimental results show that: when observations have no significant gross errors, the positioning accuracy of Helmert variance component estimation and robust component is quite similar, and slightly lower than that of elevation angle weigh function, of which the positioning accuracy is better than 2.5 m; while containing outliers, the positioning accuracy of robust solution is the highest; when the cut-off elevation angle is 30°,the positioning accuracy of the BDS single system is better than 5 m, while that of the combination system is nearly 3 m; when is 40°, its horizontal accuracy is better than 2 m, and 3D accuracy is better than 6 m, while the single system can’t be positioned.

combined BDS/GPS/GLONASS positioning; cut-off elevation angle; Helmert variance component estimation; IGIII equivalent weight function; robust estimation; positioning accuracy

引用著录：冯彪，柴洪洲，王敏，等.基于方差分量估计的不同截止高度角下的组合单点定位[J].测绘工程，2017，26(4)：32-42.

10.19349/j.cnki.issn1006-7949.2017.04.007

2016-07-20

国家自然科学基金资助项目(41574010；41274045)

冯 彪(1990-)，男，硕士研究生.

P228.4

A

1006-7949(2017)04-0032-11