强超弱紧生成Banach空间不动点性质

张 吉 超， 张 文

( 1.湖北工业大学 理学院, 湖北 武汉 430068；2.厦门大学 数学科学学院, 福建 厦门 361005 )

强超弱紧生成Banach空间不动点性质

张 吉 超*1， 张 文2

( 1.湖北工业大学 理学院, 湖北 武汉 430068；2.厦门大学 数学科学学院, 福建 厦门 361005 )

主要研究Banach空间的不动点性质,并给出一种全新的证明方法.首先利用超幂方法证明范数一致G光滑在凸集本身以及它的超幂上是相等的，然后利用反证法证明凸集在范数一致G光滑下对非扩张映射具有不动点性质,最后证明了每个强超弱紧生成的Banach空间在再赋范意义下满足每个弱紧凸集具有超不动点性质．

超弱紧集；不动点性质；Banach空间

0 引 言

文献[1]主要运用超幂方法先证明凸集具有超正规结构，然后结合凸集的超弱紧性得出该文中一个主要结果，即根据Kirk等[2]结论(一个具有正规结构的Banach空间中每个弱紧凸集对非扩张映射具有不动点性质)证明了每个强超弱紧生成空间在再赋范意义下满足每个弱紧凸集具有超不动点性质，此结论实质是Kirk等[2]结论的一个应用．本文将从超幂空间出发，运用超幂方法以及Maury[2]或者Goebel[3]关于弱紧凸集不具有不动点性质的构造方法，结合集合之间有限表示的结论，先去研究Banach空间中有界闭凸集的超不动点性质以及范数在凸集上一致G光滑的超性质，然后利用反证法直接去证明主要结论，避免去证明凸集的超正规结构，以期加强和推广超幂方法以及不动点理论中经典方法的应用，另一方面丰富凸集超不动点理论的内容．

1 预备知识

Banach空间的超性质是Banach空间理论重要组成部分之一，常见的超性质空间有超自反空间、超不动点性质空间、超正规结构空间等，具有超性质的空间均以空间之间有限表示概念为桥梁，目的是通过有限维空间性质来研究整个空间性质，因此空间之间有限表示概念在研究空间的超性质中起着重要作用．在1972年，James[4]首先提出空间之间有限表示的概念和超自反空间的概念．

定义1 设X和Y是两个Banach空间，称Y在X中有限表示，如果对每个>0和每个有限维子空间F⊂Y，存在一个有限维子空间E⊂X和一个线性映射T：F→E满足，即Banach-Mazur距离d(E，F)<1+．

定义2 称Banach空间X为超自反空间，如果对每个Banach空间Y在X中有限表示满足Y是自反空间．

文献[5]首先把定义1中的线性子空间和线性映射分别用单形和仿射映射来代替，然后提出如下集合之间有限表示概念，利用集合之间有限表示的概念，最后给出了超弱紧集的概念以及它的性质．

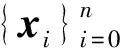
定义4 设X和Y是两个Banach空间，C⊂X，D⊂Y是两个非空子集，称D在C中有限表示，如果对每个>0和每个顶点在D中的n-单形SD，存在顶点在C中的n-单形SC和一个仿射映射T：SD→SC满足

(1-；

x，y∈SD

定义5 设C是Banach空间X中的一个非空有界闭凸子集，称C⊂X为相对超弱紧集，如果任意Banach空间Y中的每个非空有界凸子集D在C中有限表示满足D是相对弱紧集．

性质1 (1)Banach空间X中的一个有界凸子集是相对超弱紧集当且仅当它的弱闭包是超弱紧集；

(2)Banach空间X是超自反空间当且仅当BX是超弱紧集；

(3)Banach空间X中每个紧凸子集是超弱紧集；

(4)超自反空间中每个非空有界凸子集是相对超弱紧集；

(5)超弱紧集是弱紧集．

显然集合之间有限表示概念可以看作是空间之间有限表示概念的推广或局部化，而超弱紧集正好是超自反空间概念的局部化概念或推广概念．文献[5-6]继续深入研究超弱紧集的性质与特征，证明了Banach空间X中的一个有界闭凸集A是超弱紧集与集A具有有限指标性质(此概念可见文献[7])、集A具有有限对偶指标性质(此概念可见文献[8])、集A具有Δ-凸函数近似性质(此概念可见文献[9])等更多其他数学家给出的概念是等价的；关于更多超自反空间局部化概念或者推广概念可见文献[10-13]．

类似于超弱紧集的概念和强超弱紧生成空间[14]的概念，文献[1]给出了如下凸集具有超不动点性质的概念和强超弱紧生成空间的概念．在此之前，先介绍凸集具有不动点性质的概念[2]．

定义6 设C是Banach空间X中的一个非空有界闭凸集，称C具有不动点性质，如果对每个非空闭凸子集D⊆C和每个非扩张映射T：D→D满足T具有不动点，即存在x∈D满足Tx=x．

定义7 设C是Banach空间X中的一个非空有界闭凸集，称C具有超不动点性质，如果对每个Banach空间Y中的非空有界闭凸集D在C中有限表示满足D具有不动点性质．

定义8 称Banach空间X是强超弱紧生成空间，如果存在一个凸的超弱紧子集C⊂X使得对每个弱紧子集K⊂X和>0，存在正整数n∈N满足K⊂nC+BX，有时也称超弱紧集C强生成Banach空间X．

文献[1，6]证明了如下强超弱紧生成空间与空间在再赋范之间的关系，在此之前，先回顾文献[8]中范数一致G光滑概念．

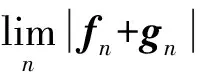
或者等价于当t→0时，有

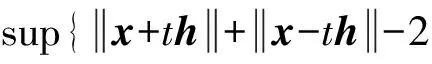
定理1 每个强超弱紧生成空间都存在一个等价的范数使得此范数限定在每个弱紧凸集上是M-一致G光滑．

空间的超性质与它的超幂空间紧密联系在一起，例如：一个Banach空间X是超自反空间当且仅当它的超幂空间是自反空间，下面回顾一下空间超幂的构造．

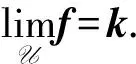
设U是N上的自由超滤子，Banach空间X的超幂空间

其中

和

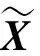
其中(xn)U是(xn)的等价类．

设C是Banach空间X中的一个非空有界闭凸集，记

显然，X通过x→(x)U等距嵌入到(X)U的一个子空间和集合C通过x→(x)U等距嵌入到(C)U的一个子集．

关于集合的超幂与集合本身有如下结论．

命题1 设C是Banach空间X中的一个非空有界闭凸集，U是N上的自由超滤子，则(C)U在C中有限表示．

命题2 设C、D分别是Banach空间X、Y中的非空有界闭凸集，如果D在C中有限表示，则存在N上的一个自由超滤子U和一个仿射等距T：aff(D)→aff(C)满足T(D)⊂(C)U．

2 主要结果

命题3 设C是Banach空间X中的一个非空有界闭凸集，则下列条件等价：

(1)C具有超不动点性质；

(2)对N上某个自由超滤子U，(C)U具有超不动点性质；

(3)对N上每个自由超滤子U，(C)U具有超不动点性质；

(4)对N上每个自由超滤子U，(C)U具有不动点性质．

证明 (1)⟹(3)：对任意Banach空间中的非空有界闭凸集E在(C)U中有限表示，由命题1知(C)U在C中有限表示以及有限表示的传递性，从而可得E在C中有限表示．根据C具有超不动点性质知E具有不动点性质，从而可得(3)是成立的．

(3)⟹(4)和(3)⟹(2)⟹(1)是显然的．

(4)⟹(1)：假设C不具有超不动点性质，则存在一个非空的有界凸集D在C中有限表示且满足D不具有不动点性质．根据命题2知存在N上的一个自由超滤子U和一个仿射等距T：aff(D)→aff(C)满足T(D)⊂(C)U，这与(C)U具有不动点性质相矛盾，故结论成立．

下列构造(关于弱紧凸集对非扩张映射的不动点性质)是证明过程中关键步骤之一，设C是Banach空间X中的一个非空弱紧凸集和存在一个非扩张映射T：C→C不具有不动点，则通过Zorn引理知，存在一个最小的弱紧凸子集K⊂C满足K不是单个元素且K对T是不变的．根据Banach压缩映象定理知K中包含T的一个近似不动点序列(xn)，即

根据上述构造，文献[3]证明了如果(xn)是T的一个近似不动点序列，则

(1)

其中x∈K．

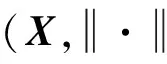
ρM(t)=ρ(M)U(t)

证明 因为M⊂(M)U，所以对任意的t∈R，显然ρM(t)≤ρ(M)U(t)成立．

对任意的(xi)U∈S(X)U，(yi)U∈(M)U，其中t∈R，令

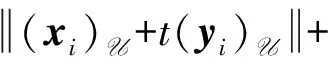
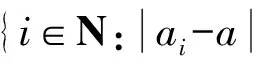
取i∈J，有

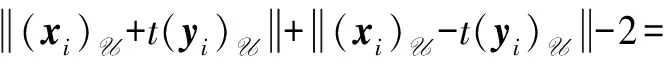
设η→0，则对任意的t∈R，有ρ(M)U(t)≤ρM(t)．

综合上述可得ρM(t)=ρ(M)U(t)．

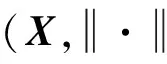
证明 假设M对非扩张映射不具有不动点性质，则存在一个最小的弱紧凸子集K⊂M满足K不是单个元素且K对T是不变的．设(xn)是T的一个近似不动点序列，不妨假设diamK=c和序列(xn)弱收敛到0∈K，通过式(1)知，对任意的x∈K，有

特别地

设t∈(0，1)，序列(xm)是序列(xn)的一个子序列，则

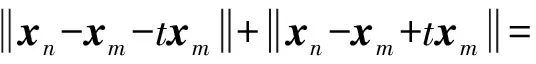
即

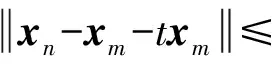
因为K是M的一个非空凸子集，所以对xm，0∈K，有(1-t)xm+t×0∈K．结合范数的下半连续性知

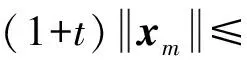
即

设m→∞，则

即

因此

推论1 超自反空间在再赋范后具有超不动点性质．

证明 由性质1以及超自反空间是由它的闭单位球强生成空间知：结论是成立的．

3 结 语

本文从反证法入手，结合超幂空间的性质，证明了某类空间在再赋范意义下具有不动点性质．此结论一方面是经典结论的推广，丰富了不动点理论的内容；另一方面在其他数学分支(如方程解的存在性等)有着广泛的运用．

[1] CHENG Lixin, CHENG Qingjin, ZHANG Jichao. On super fixed point property and super weak compactness of convex subsets in Banach spaces [J]. Journal of Mathematical Analysis and Applications, 2015, 428(2):1209-1224.

[2] KIRK W A, SIMS B. Handbook of Metric Fixed Point Theory [M]. Dordrecht:Kluwer Academic Publishers, 2001.

[3] GOEBEL K. On the structure of minimal invariant sets for nonexpansive mappings [J]. Annales Universitatis Mariae Curie-Sklodowska, 1975, 29:73-77.

[4] JAMES R C. Some self-dual properties of normed linear spaces [C] // Symposium on Infinite-Dimensional Topology. Princeton: Princeton University Press, 1972:159-175.

[5] CHENG Lixin, CHENG Qingjin, WANG Bo,etal. On super-weakly compact sets and uniformly convexifiable sets [J]. Studia Mathematica, 2010, 199(2):145-169.

[6] RAJA M. Super WCG Banach spaces [J]. Journal of Mathematical Analysis and Applications, 2016, 439(1):183-196.

[7] RAJA M. Finitely dentable functions, operators and sets [J]. Journal of Convex Analysis, 2008, 15(2):219-233.

[8] FABIAN M, MONTESINOS V, ZIZLER V. Sigma-finite dual dentability indices [J]. Journal of Mathematical Analysis and Applications, 2009, 350(2):498-507.

[9] CEPEDELLO BOISO M. Approximation of Lipschitz functions byΔ-convex functions in Banach spaces [J]. Israel Journal of Mathematics, 1998, 106:269-284.

[10] BEAUZAMY B. Opérateurs uniformément convexifiants [J]. Studia Mathematica, 1976, 57:103-139.

[11] BELLENOT S F. Local reflexivity of normed spaces, operators, and Fréchet spaces [J]. Journal of Functional Analysis, 1984, 59(1):1-11.

[12] HEINRICH S. Finite representability and super-ideals of operators [M] // Dissertationes Mathematicae. Warszawa: Panstwowe Wydawnictwo Naukowe, 1980.

[13] PIETSCH A. What is “local theory of Banach spaces”? [J]. Studia Mathematica, 1999, 135(3):273-298.

[14] SCHLÜCHTERMANN G, WHEELER R F. On strongly WCG Banach spaces [J]. Mathematische Zeitschrift, 1988, 199:387-398.

Fixed-point property of strongly super weakly compact generated Banach spaces

ZHANG Jichao*1, ZHANG Wen2

( 1.School of Science, Hubei University of Technology, Wuhan 430068, China； 2.School of Mathematical Sciences, Xiamen University, Xiamen 361005, China )

The fixed-point property of Banach space is studied and a new proof method is given. Firstly, the ultraproduct method is used to prove that the uniformlyG-differentiable norms are equivalent under convex sets and its ultraproduct. Then, by means of counter-proof, it is proven that convex sets have the fixed-point property for nonexpansive mappings under the uniformlyG-differentiable norm sense. Finally, it is shown that every strongly super weakly compact generated Banach space can be renormed so that every weakly compact convex set has super fixed-point property.

super weakly compact set; fixed-point property; Banach space

1000-8608(2017)01-0100-05

2016-07-10；

2016-12-16．

国家自然科学基金资助项目(11471270)；福建省自然科学基金资助项目(2015J01022)；厦门大学校长基金资助项目(20720160010).

张吉超*(1982-)，男，博士生，E-mail:156880717@qq.com；张 文(1977-)，男，副教授，E-mail:wenzhang@xmu.edu.cn.

O177.2

A

10.7511/dllgxb201701014