基于高速开关阀的气动人工肌肉轨迹跟踪控制仿真

谢胜龙 刘海涛 梅江平 王攀峰

(天津大学机构理论与装备设计教育部重点实验室， 天津 300072)

基于高速开关阀的气动人工肌肉轨迹跟踪控制仿真

谢胜龙 刘海涛 梅江平 王攀峰

(天津大学机构理论与装备设计教育部重点实验室， 天津 300072)

针对基于高速开关阀的气动人工肌肉位置伺服控制系统的非线性与时变性，设计了基于气动人工肌肉实验模型的PID反馈控制器，实现气动人工肌肉的高精度运动轨迹跟踪控制。首先，通过实验建模得到气动人工肌肉静态特性的实验模型，然后基于理想气体多变方程，建立可有效描述气动人工肌肉动态特性的数学模型，利用Sanville流量公式建立流经高速开关阀阀口的气体流量方程，并采用脉冲信号调制法生成PWM信号，进而控制高速开关阀占空比。在此基础上，借助PID反馈控制器建立气动人工肌肉气压与轨迹跟踪的控制模型，并采用Simulink对所提出的气压和轨迹跟踪控制方法进行数值仿真。结果表明，所建立的控制模型能够精确地跟踪期望气压和运动轨迹，从而验证了控制模型和控制方案的精确性和可行性，为实现气动人工肌肉高精度轨迹跟踪控制提供了有效手段。

开关阀； 气动人工肌肉； 轨迹跟踪； 反馈控制

引言

气动人工肌肉(Pneumatic artificial muscle， PAM)，因具有结构简单、质量轻、输出力/自重比大、柔性大等优点，在农业机器人关节驱动中得到了越来越多的应用[1]。然而，由于其自身的结构特点，使其在使用过程中产生迟滞[2]、门槛气压效应[3]、蠕变[4]、柔顺性[5]和闭环带宽低[6]等一系列现象，呈现了强非线性与时变性，给其精确的位置控制带来极大的难度。目前，气动伺服控制系统主要采用比例阀和开关阀[7]。比例阀具有高控制精度和线性行为的优点，以往研究中多采用比例阀来控制气动人工肌肉，但是其价格昂贵、结构复杂；高速开关阀[8]由于具有开关速度快和结构简单等特点，使得气动控制系统具有频响较高、成本低廉和对环境要求不高等优点。因此，使用成本低、体积小的高速开关阀代替比例阀，研究基于高速开关阀的气动人工肌肉位置伺服控制正成为当前气动人工肌肉控制技术研究的一个重要方向。

KIMURA等[9]采用反馈线性化控制方法对气动人工肌肉系统实施控制，并通过实验验证了该方法的有效性。REPPERGER等[10]基于三元素模型，在反馈线性化的基础上引入变结构控制器对气动人工肌肉的轨迹跟踪控制进行了研究。但反馈线性化方法要求模型精确且全部状态必须可测，当有不确定参数或者未建模动态特征时，不能确保控制系统的鲁棒性。AMATO等[11]采用鲁棒控制策略研究了以气动人工肌肉为驱动器的机械臂轨迹跟踪控制。ZHU等[12]采用自适应鲁棒控制实现了在无压力传感器时气动人工肌肉并联关节的轨迹跟踪，但其仅可补偿较大且缓变的系统不确定量，不能有效补偿快速变化的系统不确定量。文献[13]采用滑模控制器对气动人工肌肉进行了轨迹跟踪控制，并通过阶跃信号和正弦信号进行了实验验证，但由于系统惯性、延迟和测量误差等因素，滑模控制在滑动模态下会产生高频振动，且耗气量较大。

本文针对基于高速开关阀的气动人工肌肉位置伺服系统，提出采用基于实验模型的反馈PID控制器实现气动人工肌肉高精度运动轨迹跟踪的控制方法。首先，通过实验建模得到气动人工肌肉的实验模型；然后，基于理想气体多变方程建立其动态特性的数学模型；利用Sanville流量公式建立流经高速开关阀阀口的气体流量方程；最后，通过整合气动回路中各子系统的数学模型，建立较为完善的气动人工肌肉轨迹跟踪控制数值仿真模型。在此基础上，对控制系统进行气压与轨迹跟踪控制仿真，旨在为实现气动人工肌肉的高精度轨迹跟踪控制提供有效手段。

1 系统描述

图1为气动人工肌肉轨迹跟踪原理图。相关元器件型号如表1所示。其中，气源经过减压阀和储气罐连接高速开关阀组，高速开关阀1为进气阀(以下简称进气阀)，高速开关阀2为排气阀(以下简称排气阀)。当高速开关阀通电时，阀口打开；当高速开关阀断电时，阀口关闭。开关阀组通过进气和排气控制气动人工肌肉的伸缩。具体工作原理如下：高速开关阀的初始状态均为断电状态，气动人工肌肉内腔与大气压相通，处于自然状态；当进气阀通电且排气阀断电时，气源中的高压气体经储气罐进入气动人工肌肉内腔，随着进气量的增加，气动人工肌肉在轴向不断收缩；当气动人工肌肉收缩至期望位置时，进气阀和排气阀同时断电，此时高压气体滞留在气动人工肌肉内腔，气动人工肌肉保持当前状态；当进气阀断电且排气阀通电时，气动人工肌肉内腔高压气体经排气阀阀口由消音器排出。

图1 气动人工肌肉轨迹跟踪控制原理图Fig.1 Scheme of pneumatic muscle tracking control1.气动人工肌肉 2.气压传感器 3.位移传感器 4.高速开关阀1 5.截止阀 6.消音器 7.高速开关阀2 8.储气罐 9.节流阀 10.气源

在采用PWM信号控制高速开关阀的过程中，当气动人工肌肉的理想收缩量与位移传感器实际测得的位移信号偏差较大时，为使气动人工肌肉迅速地到达设定位置，相应的高速开关阀应完全打开；当气动人工肌肉接近设定位置时，高速开关阀PWM控制信号占空比随位移偏差相应改变，当位移偏差小于设定范围(死区)时，为避免气动人工肌肉在设定位置附近频繁地振荡，认为气动人工肌肉到达设定位置，此时关闭相应的高速开关阀，使气动人工肌肉保持在当前位置。

表1 各元部件型号
Tab.1 Components of system

元件型号主要参数厂商气动人工肌肉DMSP20500N长500mm,内径20mm费斯托位移传感器TEX0150415002205量程150mmNovetechnik气压传感器SDE1D10G2WQ4LPUM8G5最大测量气压1MPa费斯托高速开关阀MHE2MS1H3/2GM7K3位2通,常闭,响应速度2ms费斯托数据采集卡PCI625432路模拟量输入,48路模拟量输出美国NI公司

2 系统建模

2.1 气动人工肌肉

2.1.1 气动人工肌肉静态模型

气动人工肌肉的静态特性模型反映的是气动人工肌肉的拉力与其内腔气压及长度间的函数关系。目前，常用的气动人工肌肉静态特性模型有：Chou模型[14]和Tondu模型[15]。由于收缩率ε比编织角α更易于通过实验测得，因此实际应用中多采用Tondu公式或其修正公式。气动人工肌肉的Tondu模型[16]为

(1)

其中

式中r0——气动人工肌肉在初始状态下的半径L0——气动人工肌肉在初始状态下的长度L——气动人工肌肉充气收缩后的长度p——气动人工肌肉内腔气压

式(1)表明气动人工肌肉的拉力与气压p呈正比，与收缩率ε呈非线性关系。

由于气动人工肌肉某些内部结构参数数值难以准确获取，且气动人工肌肉几何模型在低压下精度较差，同时现有的理论模型难以完全模拟气动人工肌肉的静态特性，使得实现气动人工肌肉的精确位置控制比较困难。为此，本文采用实验方法建立气动人工肌肉的静态特性模型，即利用实验数据拟合气动人工肌肉收缩力与其内腔气压及位移之间的函数关系。具体实验方案如图2所示。

图2 气动人工肌肉等长实验装置Fig.2 Isometric setup of pneumatic artificial muscle

气动人工肌肉在不同长度下的充气压力与收缩力之间的关系曲线如图3所示。

图3 气动肌肉收缩力与气压之间关系Fig.3 Relations between pressure and contracting force

从图3可以看出，在不同长度下，气动人工肌肉的收缩力与气压呈正比。因此，可将气动人工肌肉的收缩力与气压以及气动人工肌肉的长度表示为[17]

Fconst=a(x)p+b(x)

(2)

其中

a(x)=a0+a1x+a2x2

(3)

b(x)=b0+b1x+b2x2+b3x3

(4)

式中Fconst——气动人工肌肉收缩力x——气动人工肌肉长度a(x) ——直线斜率b(x) ——直线截距ai、bj——待拟合的参数

根据测得的实验数据，利用Matlab曲线拟合工具箱得到式(3)与式(4)中的系数ai和bj，拟合结果为

(5)

根据气动人工肌肉的数学模型，在Simulink中搭建其仿真模型如图4所示。给定负载F和气压p，便可得到气动人工肌肉长度随其内腔气压的变化曲线。

图4 气动人工肌肉静态特性仿真图Fig.4 Static characteristic simulation diagram of pneumatic artificial muscle

2.1.2 气动人工肌肉动态模型

由于气动人工肌肉乳胶管由弹性尼龙材料构成，且在气动人工肌肉伸缩过程中仅透过很少的热量，故可将气动人工肌肉的伸缩过程视为等温或绝热过程。由理想气体多变方程可得到气动人工肌肉体积与内腔气压之间的函数关系[18]

(6)

对式(6)全微分可得

(7)

相应的Simulink模块如图5所示。模块输入量为流进气动人工肌肉的气体质量流量，当假设气动人工肌肉体积恒定时，式(7)中第2项为0，经积分后即可得到气动人工肌肉的内腔气压。

图5 气动人工肌肉动态特性仿真图Fig.5 Dynamic characteristic simulation diagram of pneumatic muscle

2.2 高速开关阀

气体通过阀口的过程十分复杂，通常采用Sanville流量公式[19]进行描述，即

(8)

式(8)将阀口的气体流动过程近似为理想气体通过收缩喷管的一维等熵流动。当开关阀阀口全开时，可将其等效为光滑的收缩喷管。保持上游压力和温度不变，当pd/pu≤0.528时，气体进入壅塞流态，该值称为临界压力比[20]。

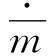
(9)

式中μ——高速开关阀PWM信号的占空比Am——阀口最大有效截面积

由文献[21]可知，MHE2-MS1H-3/2G-M7-K型气动人工肌肉的阀口最大面积Am为1.819 4×10-6m2。

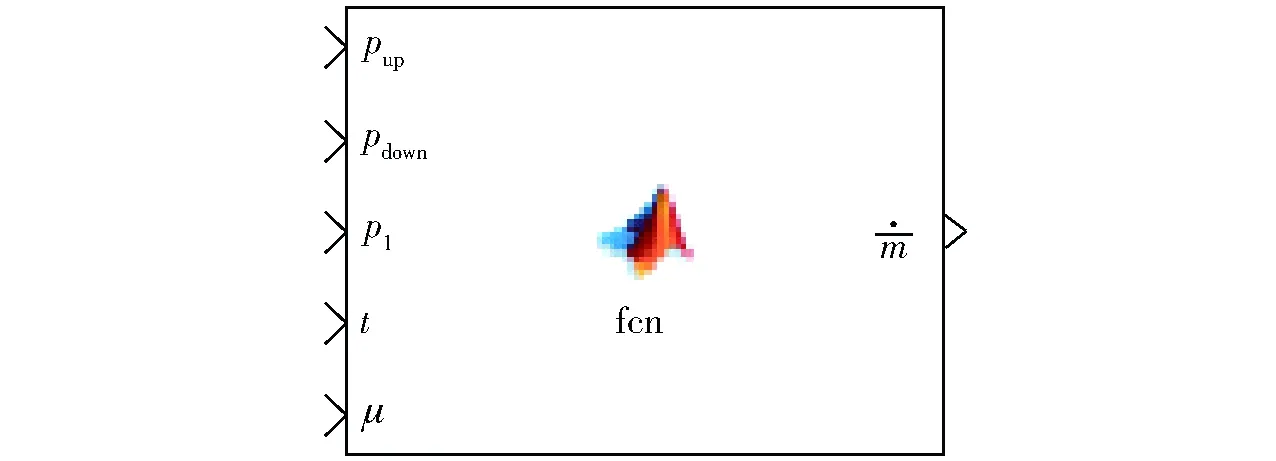
图6 开关阀流量特性模块Fig.6 Mass flux characteristics of on/off valve

2.3 PWM信号

图7 PWM信号生成仿真图Fig.7 Simulation diagram of PWM generation

Simulink中有多种产生PWM信号的方法，本文采用文献[22]中介绍的脉冲信号调制法产生PWM信号。该方法具有方便快捷、线性关系明确等优点。其步骤如下：首先产生占空比为50%的标准脉冲信号序列，然后通过偏置与积分的方法得到标准的三角波信号，最后通过对三角波信号进行偏置来获得所需的PWM 信号。采用该方法建立的仿真模型如图7所示。

Pulse Generator模块用于产生幅值为2，占空比为50%的方波，减1偏置后积分，即可生成用于调制PWM波的三角波调制信号。将输入信号与三角波调制信号之差输入Relay模块，当输入大于0时，Relay输出1(模拟充气过程)；当输入小于0时，Relay输出-1(模拟放气过程)，即可将输入信号调制成控制高速开关阀的PWM信号。

3 系统仿真

采用PID反馈控制进行气动人工肌肉气压与轨迹跟踪控制的仿真。根据期望信号与反馈信号的差值，利用PID控制器得出高速开关阀占空比信号，从而控制气动人工肌肉的进气量与排气量，进而控制其内部气压与位移。

PID反馈控制的数学模型为

(10)

式中 e(t)——输入信号 u(t)——输出信号 Kp——比例系数 Ki——积分系数 Kd——微分系数

比例系数用于设置信号差值的放大系数，适当提高比例系数，能够加快系统响应性；为了消除引入比例系数所产生的超调和震荡，引入积分系数，使经过比例系数放大后的信号在积分时间内逐渐增大(或减小)，抑制振荡的产生，消除稳态误差。微分系数根据差值信号变化的速率，提前给出一个调节动作，从而加快系统的动作速度，减少调节时间；且能够克服因积分时间过长而使系统响应滞后的缺陷。

3.1 气压控制

气压控制是气动人工肌肉轨迹跟踪控制的基础，并可以初步验证所建模型的准确性。气压跟踪控制系统原理图与仿真模型如图8、9所示。

图8 气压跟踪控制原理图Fig.8 Scheme of pressure tracking control

输入期望气压pd，与反馈回的实际气压pt相减，并经过PID控制器调节得到高速开关阀的占空比信号，通过占空比信号中高电平的占空比调节高速开关阀阀口大小，从而调节流经高速开关阀进入气动人工肌肉内腔的空气流量，进而实现调节气动人工肌肉内腔气压。这里分别输入正弦波气压和方波气压信号，给定PID参数P=1.5、I=0.000 01和D=0.000 01，仿真结果如图10～13所示。

图9 气压跟踪控制系统仿真模型Fig.9 Simulation model of pressure tracking control system

图10 正弦波气压跟踪Fig.10 Sinusoidal pressure tracking

图11 正弦波气压跟踪误差Fig.11 Error of sinusoidal pressure tracking

其中，图10和图12分别为气动人工肌肉内腔气压对正弦气压和方波气压的跟踪效果；图11和图13分别为正弦波和方波的气压跟踪误差。图13中方波气压跟踪误差的突变是由于在此处期望气压与仿真气压存在微小不同步所导致。可见所建模型对正弦信号跟踪效果非常理想，从而验证了模型的精确性。

图12 方波气压跟踪Fig.12 Square wave pressure tracking

3.2 轨迹跟踪控制

气动人工肌肉轨迹跟踪控制系统原理图和仿真模型分别如图14和图15所示。

输入期望位移，与反馈回的位移相减，并经过PID控制器调节得到高速开关阀占空比信号，从而调节流经高速开关阀进入气动人工肌肉内腔的空气流量，进而调节气动人工肌肉内腔的气压及其长度。设置仿真类型为定步长仿真，步长为0.001 s，仿真时间为10 s，求解器为ODE4，PWM信号周期为20 ms。分别跟踪频率为0.2 Hz，幅值为10 mm的正弦波信号和方波信号。被跟踪的正弦波与方波曲线为

图14 轨迹跟踪控制系统原理图Fig.14 Scheme of trajectory tracking control

图15 气动人工肌肉轨迹跟踪控制系统仿真模型Fig.15 Simulation model of trajectory tracking control

f(t)=10sin(0.4πt)+450

(11)

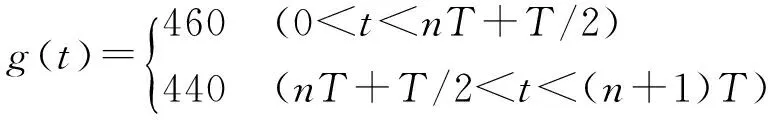
(12)

式中f(t)——正弦波信号g(t)——方波信号T——方波信号周期

给定PID参数P=0.08、I=0.000 001和D=0.000 01，仿真结果如图16～19所示。

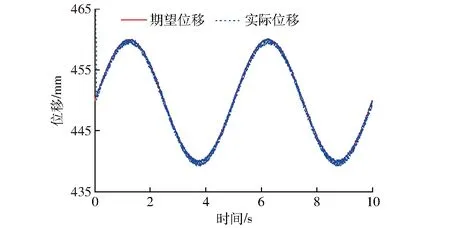
图16 正弦波轨迹跟踪Fig.16 Sinusoidal trajectory tracking

图17 正弦波轨迹跟踪误差Fig.17 Errors of sinusoidal trajectory tracking

图18 方波轨迹跟踪Fig.18 Square wave trajectory tracking

其中，图16和图18分别为气动人工肌肉对正弦和方波轨迹的跟踪效果；图17和图19分别为正弦波和方波的轨迹跟踪误差。类似地，图19中方波位移跟踪误差的突变是由于在此处期望位移与仿真位移存在微小的不同步所导致。由图16～19可见，无论输入信号为正弦波信号或是方波信号，气动人工肌肉轨迹跟踪控制的跟踪效果均较好，误差整体分布都较为均匀，平均误差约为0.5 mm，最大误差仅为0.8 mm。可见仿真模型的精度较高，从而验证了所建立的控制系统数学模型的正确性。

4 结论

(1) 在气动人工肌肉等长实验的基础上，建立了气动人工肌肉静态特性的实验模型，更真实地反映了气动人工肌肉的静态特性，提高了所建气动人工肌肉静态特性模型的精度。

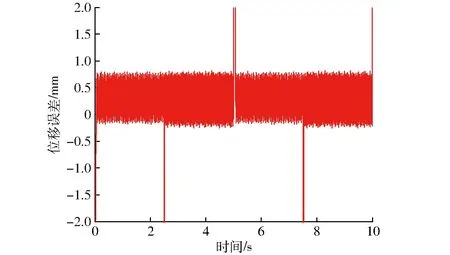
图19 方波轨迹跟踪误差Fig.19 Errors of square wave trajectory tracking

(2) 在理论分析的基础上建立了气动人工肌肉运动控制系统的数学模型，并采用Simulink模拟了所建模型对气压和轨迹的跟踪效果。结果表明，所建的控制模型能很好地实现气动人工肌肉的气压与轨迹跟踪控制。

1 王斌锐, 周唯逸, 许宏. 智能气动肌肉的静态驱动特性研究[J]. 农业机械学报, 2009, 40(3):208-212. WANG B R, ZHOU W Y, XU H. Static actuating characteristics of intelligent pneumatic muscle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(3):208-212.(in Chinese)

2 VO-MINH T, TJAHJOWIDODO T, RAMON H, et al. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(1):177-186.

3 OBIAJULU S C, ROCHE E T, PIGULA F A, et al. Soft pneumatic artificial muscles with low threshold pressures for a cardiac compression device[C]∥ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2013, 6A:1-8.

4 VO-MINH T, KAMERS B, RAMON H, et al. Modeling and control of a pneumatic artificial muscle manipulator joint—Part I: Modeling of a pneumatic artificial muscle manipulator joint with accounting for creep effect[J]. Mechatronics, 2012, 22(7):923-933.

5 DAERDEN F, LEFEBER D. Pneumatic artificial muscles: actuators for robotics and automation[J]. European Journal of Mechanical and Environmental Engineering, 2002, 47(1):11-21.

6 CALDWELL D G, Medrano-Cerda G, GOODWIN M. Control of pneumatic muscle actuators[J]. IEEE Control Systems, 1995, 15(1):40-48.

7 杨钢. 气动人工肌肉位置伺服系统研究及其应用[D]. 武汉: 华中科技大学, 2004. YANG G. Research on pneumatic muscle actuator position servo system and its application[D]. Wuhan: Huazhong University of Science and Technology, 2004.(in Chinese)

8 BEHROUZ N S, MASOUD B, MOHAMMAD J F. Modelling and controller design of electro-pneumatic actuator based on PWM[J]. International Journal of Robotics and Automation, 2012, 1(3):125-136.

9 KIMURA T, HARA S, FUJITA T, et al. Feedback linearization for pneumatic actuator systems with static friction[J]. Control Engineering Practice, 1997, 5(10):1385-1394.

10 REPPERGER D W, JOHNSON K R, PHILIPS C A. Nonlinear feedback controller design of a pneumatic muscle actuator system[C]∥1999 American Control Conference,IEEE, 1999: 1525-1529.

11 AMATO F, COLACINO D, COSENTINO C, et al. Robust and optimal tracking control for manipulator arm driven by pneumatic muscle actuators[C]∥2013 IEEE International Conference on Mechatronics (ICM), 2013: 827-834.

12 ZHU X C, TAO G L, YAO B, et al. Adaptive robust posture control of a parallel manipulator driven by pneumatic muscles[J]. Automatica, 2008, 44(9):2248-2257.

13 SHEN X. Nonlinear model-based control of pneumatic artificial muscle servo systems[J]. Control Engineering Practice, 2010, 18(3):311-317.

14 CHOU C P, BLAKE Hannaford. Measurement and modeling of McKibben pneumatic artificial muscles[J]. IEEE Transactions on Robotics and Automation, 1996, 12(1):90-102.

15 TONDU B, LOPEZ P. Modeling and control of McKibben artificial muscle robot actuators[J]. IEEE Control Systems,2000, 20(2):15-38.

16 TONDU B, IPPOLITO S, GUIOCHET J, et al. A seven-degrees-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots[J]. The International Journal of Robotics Research, 2005, 24(4):257-274.

17 PUJANA A A, Mendizabal A, Arenas J, et al. Modelling in modelica and position control of a 1-dof set-up powered by pneumatic muscles[J]. Mechatronics, 2010, 20(5):535-552.

18 VO-MINH T, TJAHJOWIDODO T, RAMON H, et al. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation[J]. Mechatronics, 2010, 20(3):402-414.

19 沈文臣, 胡宇辉, 余天啸,等. 气动换挡执行机构压力特性仿真与试验[J/OL]. 农业机械学报, 2016，47(2):338-348. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160245&flag=1. DOI：10.6041/j.issn.1000-1298.2016.02.045. SHEN W C, HU Y H, YU T X, et al. Simulation and experiment of pressure characteristics for pneumatic shifting actuator[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(2):338-348.(in Chinese)

20 王晓龙. 基于高速开关阀的气动高精度运动控制系统关键技术研究[D]. 杭州: 浙江大学, 2013. WANG X L. Study on key technologies of high precision motion control of a pneumatic system using high speed solenoid valves[D]. Hangzhou: Zhejiang University, 2013.(in Chinese)

21 孟德远, 陶国良, 李艾民, 等. 高速开关阀控气动位置伺服系统的自适应鲁棒控制[J]. 机械工程学报, 2015, 51(10):180-188. MENG D Y, TAO G L, LI A M, et al. Adaptive robust control of pneumatic cylinders using fast switching on/off solenoid valves[J]. Journal of Mechanical Engineering, 2015, 51(10):180-188.(in Chinese)

22 REN B S, PAN J, SHI G L. A new flight simulator driven by pneumatic artificial muscles[C]∥Proceedings of the 7th International Conference on Fluid Power Conference, 2009: 507-510.

Simulation of Tracking Control of Pneumatic Artificial Muscle Based on Fast Switching Valves

XIE Shenglong LIU Haitao MEI Jiangping WANG Panfeng

(KeyLaboratoryofMechanismTheoryandEquipmentDesign,MinistryofEducation,TianjinUniversity,Tianjin300072,China)

Due to the problem of nonlinear and time-varying exists in the model of the pneumatic artificial muscle (PAM) trajectory tracking control system, the modeling of the trajectory tracking control of PAM driven by fast switching valves was detailed in order to enhance the trajectory tracking control accuracy of PAM and reduce the cost of control scheme. A feedback PID controller based on the experimental model of PAM was proposed to achieve its high accuracy trajectory tracking control. The control system was divided into three subsystems, which were pneumatic artificial muscle, fast switching valve and the PWM signal. Firstly, the static model of PAM was established by the isometric experiment, and then the dynamic characteristic model of PAM was developed based on the polytropic equation, in which the air mass flow rate through the fast switching valve was evaluated by using the Sanville equation. The PWM signal that was used to control the fast switching valves was generated referring to the pulse signal modulation method. Sequentially, the pressure and trajectory tracking control models of PAM were derived by means of feedback PID controller, based on which the simulations of pressure and trajectory tracking control were implemented in the environment of Matlab/Simulink. The results indicated that the control model can achieve satisfactory performance and accuracy, which validated the feasibility of the proposed model and control scheme. Thus, it provided an effective approach for high accuracy trajectory tracking control of PAM.

fast switching valve; pneumatic artificial muscle; trajectory tracking; feedback control

10.6041/j.issn.1000-1298.2017.01.049

2016-06-01

2016-08-15

国家自然科学基金项目(51405331)

谢胜龙(1988—)，男，博士生，主要从事机器人理论与应用研究，E-mail: sleepinglion@tju.edu.cn

刘海涛(1981—)，男，副教授，主要从事机构学与机器人学研究，E-mail: liuht@tju.edu.cn

TH122

A

1000-1298(2017)01-0368-07