偏心-椭圆齿轮行星轮系栽植装置动力学优化与试验
王 英 夏旭东 何小晶 赵 雄 陈建能
(1.宁波大学机械工程与力学学院, 宁波 315211; 2.浙江理工大学机械与自动控制学院, 杭州 310018)
偏心-椭圆齿轮行星轮系栽植装置动力学优化与试验
王 英1夏旭东2何小晶2赵 雄2陈建能2
(1.宁波大学机械工程与力学学院, 宁波 315211; 2.浙江理工大学机械与自动控制学院, 杭州 310018)
为获得偏心-椭圆齿轮行星轮系栽植装置最优的机构参数,在建立其动力学分析模型的基础上,以一个作业循环中支座垂直方向所受作用力的峰值力和波动最小为目标建立其动力学优化模型。为验证所建立的动力学分析模型的可靠性,以该装置满足理想栽植要求的非劣解集为约束条件,运用所建立的动力学优化模型优化得到该装置最优的机构参数,进而基于最优机构参数搭建试验台进行动力学特性测试,测得了该栽植装置在工作转速为40 r/min时一个工作循环中支座垂直方向受力与行星架转角的关系,通过试验结果和理论结果的对比分析,表明其动力学分析模型是可靠的,可为其动力学优化提供可靠数学模型。
钵苗移栽机; 非圆齿轮行星轮系; 栽植装置; 动力学分析; 优化; 试验
引言
旱地钵苗移栽机是一种将达到秧龄的钵苗移栽到大田中的机器。不管是半自动移栽机[1-3](人工取苗并将其喂入栽植嘴,栽植装置将栽植嘴内的钵苗植入大田)还是全自动移栽机[4-5](取苗和栽植分别由取苗装置和栽植装置完成)都有一套栽植装置,它是将钵苗植入大田的最终部件,直接影响移栽后钵苗的立苗率和损伤率,从而影响成活率和产量,因此栽植装置的性能直接影响整台移栽机的作业性能。为满足高速移栽机高立苗率和低损伤率的作业要求,陈建能等[6-11]基于非圆齿轮行星轮系提出了一系列栽植装置,并建立了其运动学分析模型和满足理想栽植要求的多目标参数优化模型,得到了满足理想栽植要求的多种栽植装置,且每种栽植装置的优化结果都是一系列非劣解[10-11],而要获得最优的栽植装置机构参数,需进一步进行动力学分析和优化。为此本文以非圆齿轮行星轮系栽植装置系列中的偏心-椭圆齿轮行星轮系栽植装置为研究对象,在建立其动力学分析和优化模型的基础上,对其进行优化求解得到其最优机构参数,进而进行试验研究,以验证所建立的动力学分析模型的可靠性。
1 非圆齿轮行星轮系栽植装置

图1 非圆齿轮行星轮系栽植装置结构图Fig.1 Structure graph of planting device driven by planetary non-circular gears1.中心轴 2.支座 3.行星架壳体 4.行星轴 5.端面凸轮 6.摆杆 7.接苗斗 8.外半栽植嘴 9.内半栽植嘴 10.弹簧 11.行星轮 12.第二中间轮 13.第一中间轮 14.太阳轮
非圆齿轮行星轮系栽植装置如图1所示,动力由中心轴输入,中心轴带动行星架壳体匀速转动,行星架转动时,带动行星架壳体内的非圆齿轮转动,其中第一中间轮与太阳轮啮合,第二中间轮与行星轮啮合,太阳轮两侧是对称结构。栽植嘴通过接苗斗与行星轴固联,端面凸轮与行星架壳体固联,当行星轴相对行星架壳体转动时,栽植嘴上的摆杆相对端面凸轮摆动,实现内外半栽植嘴对中开合。内外半栽植嘴的回位依靠弹簧的弹力,弹簧两头分别挂在内半栽植嘴和外半栽植嘴上。
第一中间轮与太阳轮组成的齿轮副和第二中间轮与行星轮组成的齿轮副,可以选择变性椭圆-共轭非圆齿轮副、变性偏心圆-共轭非圆齿轮副、变性巴斯噶蜗线非圆齿轮副、变性傅里叶非圆齿轮副和变性正弦非圆齿轮副5类非圆齿轮副,这样总共可组成25种不同的非圆齿轮行星轮系栽植装置。当第一中间轮与太阳轮组成的齿轮副为变性偏心圆-共轭非圆齿轮副,第二中间轮与行星轮组成的齿轮副为变性椭圆-共轭非圆齿轮副时,该栽植装置简称偏心-椭圆齿轮行星轮系栽植装置。
2 偏心-椭圆齿轮行星轮系栽植装置动力学分析模型的建立
在建立动力学分析模型时,将栽植装置分为开穴部分和驱动部分,其中开穴部分为栽植嘴,驱动部分为非圆齿轮行星轮系,分别建立各部分的动力学分析模型,分析模型中与运动学特性相关的变量由偏心-椭圆齿轮行星轮系栽植装置运动学分析[10]得到。
2.1 开穴部分的动力学分析模型
2.1.1 控制栽植嘴张闭的端面凸轮所受作用力
以行星轮转动中心B为原点,水平方向为x轴,垂直方向为y轴,凸轮转动轴线为z轴,建立如图2所示的坐标系Bxyz。为方便分析,以摆杆平行线为x′轴,凸轮转动轴线为z′轴,建立如图2所示的动坐标系Bx′y′z′。

图2 摆动从动件端面凸轮机构的受力分析图Fig.2 Force analysis diagrams of end cam with oscillating follower
端面凸轮压力角[12-13]
(1)
由图中关系可知端面凸轮对摆杆作用力FE沿x′、y′、z′方向的分力分别为
式中μ、Rb——端面凸轮压力角、基圆柱半径ψ——摆杆角位移ψ0——摆杆初始位置角LA′E——摆杆旋转中心A′到滚子中心E的距离(摆杆的有效长度)
δ——端面凸轮相对摆杆的角位移
FE——端面凸轮对摆杆作用力
μ1——滚子与凸轮之间的摩擦角
2.1.2 摆杆和内半栽植嘴动力学平衡方程
摆杆和内半栽植嘴固联,作空间复合运动,一方面在x′y′平面绕行星轮轴心B转动,另一方面在x′z′平面绕旋转轴AA′转动,其受力分析如图3所示。

图3 摆杆和内半栽植嘴受力分析图Fig.3 Force analysis diagram of oscillating bar and inside half part of planting nozzle
建立其动力学平衡方程为
(5)
(6)
(7)
(8)
其中
x′E=x′A-LA′Esinθ1z′E=z′A-LA′Ecosθ1
x′F=x′A+LA′Fcosθ2x′C1=x′A-LA′C1sinθ3
z′C1=z′A-LA′C1cosθ3x′C2=x′A+LA′C2cosθ4
z′C2=z′A+LA′C2sinθ4θ1=ψ+ψ0
θ2=θ20-ψθ3=θ30+ψθ4=θ40-ψ
式中FAx′、FAy′、FAz′——摆杆旋转中心A受力在动坐标系沿x′、y′、z′方向分量
mC1——摆杆的质量
mC2——内半栽植嘴的质量
α——动坐标与静坐标的夹角
(x′A,y′A,z′A)——摆杆旋转中心A在动坐标系中的坐标

(x′C1,y′C1,z′C1)——摆杆质心C1在动坐标系中的坐标
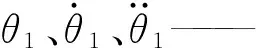
(x′C2,y′C2,z′C2)——内半栽植嘴质心C2在动坐标系中的坐标
FFz′——弹簧对栽植嘴的作用力
JC1y——摆杆绕A点x′z′平面的转动惯量
JC2y——内半栽植嘴绕A点x′y′平面的转动惯量
(x′E,y′E,z′E)——滚子中心E在动坐标系中的坐标
(x′F,y′F,z′F)——弹簧作用点F在动坐标系中的坐标
LA′F——摆杆旋转中心A′到弹簧作用点F的距离
θ2——弹簧作用点F和摆杆旋转中心A′连线与x′方向的夹角
θ20——θ2初始值
LA′C1——摆杆旋转中心A′到质心C1的距离
θ3——摆杆质心C1和摆杆旋转中心A′ 连线与z′方向的夹角
θ30——θ3初始值θ40——θ4初始值
LA′C2——摆杆旋转中心A′点与质心C2距离
θ4——内半栽植嘴质心C2和摆杆旋转中心A′连线与x′方向的夹角
2.1.3 开穴部分动力学方程的求解
由式(2)、(4)、(8)可求得FE、FEx′、FEz′;将FEx′代入式(5)可求得FAx′;将FEz′代入式(7)可求得FAz′;由式(6)可求得FAy′。
2.2 驱动部分的动力学分析模型
2.2.1 太阳轮动力学平衡方程
太阳轮固定不动,受到机架和对称布置在其两侧的上、下两个第一中间轮的作用力,其受力分析如图4所示。

图4 太阳轮受力分析图Fig.4 Force analysis diagram of sun gear
建立其动力学平衡方程为
∑Fx=FP′x+FPx+FOx=0
(9)
∑Fy=FP′y+FPy+FOy-m1g=0
(10)
∑MO1=-FPxyP+FPyxP-FP′xyP′+
FP′yxP′-m1gxCO+M1=0
(11)
其中
FP′x=FPx(φ-π)FP′y=FPy(φ-π)
式中FP′x、FP′y——对称侧第一中间轮在啮合点P′处对太阳轮的作用力在x、y方向的分量
FPx、FPy——第一中间轮在啮合点P处对太阳轮的作用力在x、y方向分量
FOx、FOy——机架对太阳轮的作用力在x、y方向的分量
m1——太阳轮质量
(xP,yP)——第一中间轮与太阳轮的啮合点P的坐标
(xP′,yP′)——对称侧第一中间轮与太阳轮的啮合点P′的坐标
(xCO,yCO)——太阳轮质心坐标
M1——太阳轮所受的阻力矩
2.2.2 中间轮动力学平衡方程
第一中间轮和第二中间轮固定在同一根轴上,其中第一中间轮受到太阳轮的作用力,第二中间轮受到行星轮的作用力,且二者同时受到行星架的作用力,则受力分析如图5所示。

图5 中间轮受力分析图Fig.5 Force analysis diagram of middle gears
建立其动力学平衡方程为
(12)
(13)
(14)
其中
FPx=FNPcos(φ+π/2+φP1)+FfPcos(φ+π/2+φP2)
(15)
FPy=FNPsin(φ+π/2+φP1)+FfPsin(φ+π/2+φP2)
(16)
式(15)、(16)中,当MP<0时
当MP>0时
式中FQx、FQy——行星轮在啮合点Q处对中间轮的作用力在x、y方向的分量
FA1x、FA1y——行星架对中间轮轴的作用力在x、y方向的分量
m2——中间轮质量
(xA1,yA1)——中间轮转动中心坐标
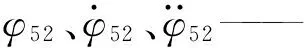
(xCA,yCA)——中间轮质心坐标

MP——太阳轮对中间轮的啮合力矩
r6——中间轮转动中心A1到啮合点Q距离
γ——两级非圆齿轮转动中心连线的夹角
J56A1——中间轮绕A1点的转动惯量
FNP——啮合点P的正压力
FfP——啮合点P的摩擦力
ξ1(φ)——太阳轮节曲线在啮合点P的切线方向与向径的夹角
r5——中间轮转动中心A1到啮合点P距离
μ2——齿轮摩擦角
2.2.3 行星轮(含行星轮轴和接苗斗)动力学平衡方程
行星轮与第二中间轮啮合,受到第二中间轮的作用力,行星轮轴受到行星架的作用力,接苗斗受到内外半栽植嘴的作用力(由开穴部分受力分析可知),则行星轮(含行星轮轴和接苗斗)受力分析如图6所示。
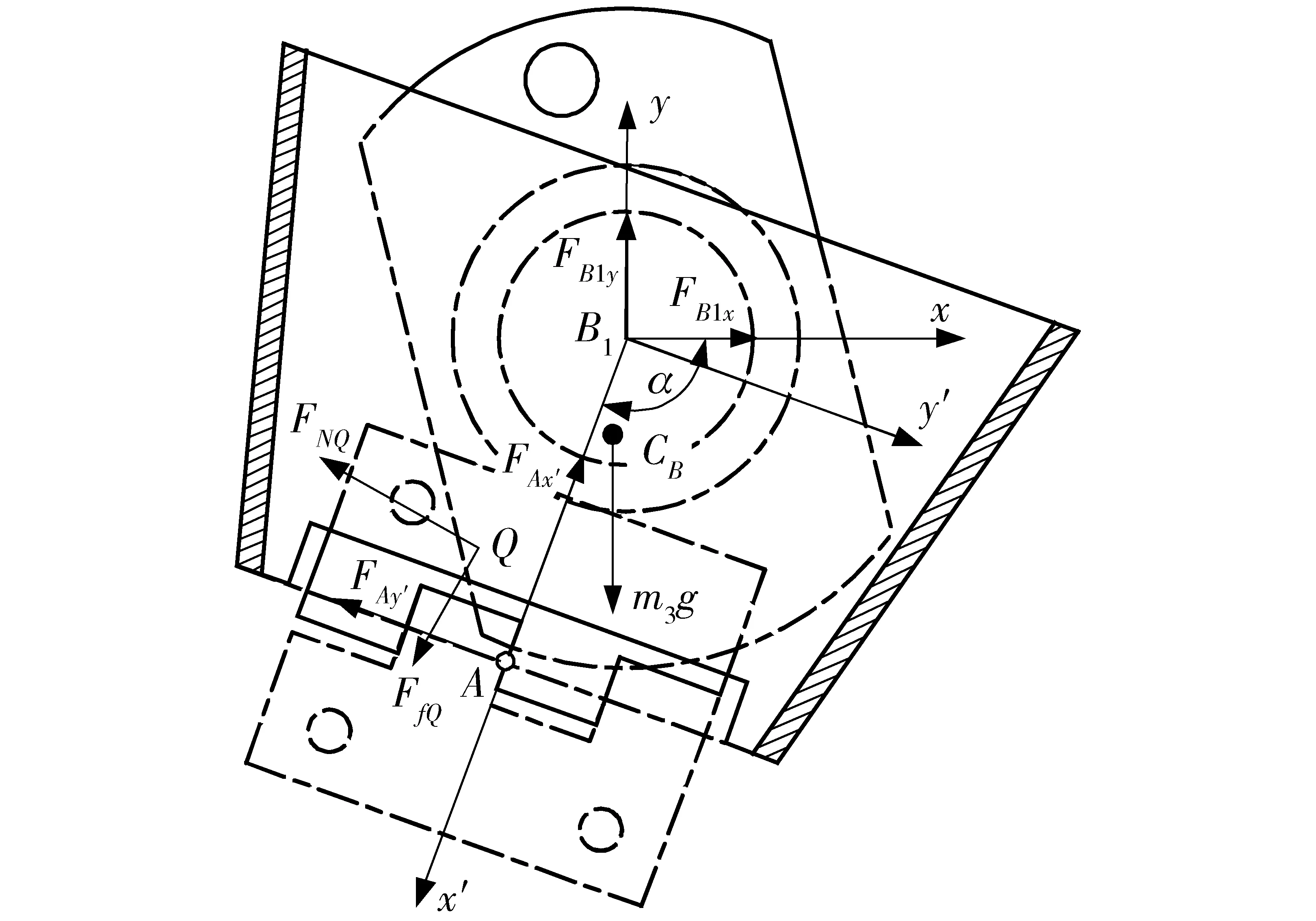
图6 行星轮受力分析图Fig.6 Force analysis diagram of planetary gears
建立其动力学平衡方程为
(17)
(18)
∑Fz=FB1z-FAz′=0
(19)
(20)
其中
FQx=FNQcos(φ+π/2+γ+φQ1)+
FfQcos(φ+π/2+γ+φQ2)
(21)
FQy=FNQsin(φ+π/2+γ+φQ1)+
FfQsin(φ+π/2+γ+φQ2)
(22)
MT=FEx′y′E
(23)
式(21)、(22)中,当MQ<0时
当MQ>0时
式中FB1x、FB1y、FB1z——行星架对行星轮轴的作用力在x、y、z方向的分量
m3——行星轮(行星轮轴和接苗斗)质量
(xCB,yCB)——行星轮质心坐标
(xB1,yB1)——行星轮转动中心坐标
MQ——中间轮对行星轮的啮合力矩
MT——摆杆对端面凸轮的阻力矩
J7B1——行星轮(含行星轮轴和接苗斗)绕B1点的转动惯量
FNQ——啮合点Q的正压力
FfQ——啮合点Q的摩擦力
ξ2(φ)——中间轮节曲线在啮合点Q的切线方向与向径的夹角
r7——行星轮转动中心B1到啮合点Q距离
2.2.4 行星架动力学平衡方程
行星架受到太阳轮轴、中间轮轴、行星轮轴和端面凸轮的作用力,其受力分析如图7所示。
建立其动力学平衡方程为
∑Fx=FO1x-FA1x-FB1x-FA′1x-FB′1x=0
(24)
∑Fy=FO1y-FA1y-FB1y-FA′1y-FB′1y-m4g=0
(25)
∑Fz=FO1z-FB1z-FB′1z=0
(26)
∑MO1=-FA′1yxA′1-FB′1yxB′1+FA′1xyA′1+
FB′1xyB′1-FA1yxA1-FB1yxB1+FA1xyA1+
FB1xyB1+ML+MT+MT(φ-π)=0
(27)

图7 行星架受力分析图Fig.7 Force analysis of planetary carrier
其中
FA′1x=FA1x(φ-π)FA′1y=FA1y(φ-π)
FB′1x=FB1x(φ-π)FB′1y=FB1y(φ-π)
FB′1z=FB1z(φ-π)xA′1=xA1(φ-π)=-xA1
yA′1=yA1(φ-π)=-yA1xB′1=xB1(φ-π)=-xB
yB′1=yB1(φ-π)=-yB
故式(27)可转换为
∑MO1=(FA1x-FA′1x)yA1-(FA1y-FA′1y)xA1+
(FB1x-FB′1x)yB1-(FB1y-FB′1y)xB1+ML+
MT+MT(φ-π)=0
(28)
式中FO1x、FO1y、FO1z——太阳轮轴对行星架的作用力在x、y、z方向的分量
FA′1x、FA′1y——对称侧行星架对中间轮轴的作用力在x、y方向的分量
FB′1x、FB′1y、FB′1z——对称侧行星架对行星轮轴的作用力在x、y、z方向的分量
m4——行星架质量
(xA′1,yA′1)——对称侧中间轮转动中心坐标
(xB′1,yB′1)——对称侧行星轮转动中心坐标
ML——电动机输入转矩
2.2.5 驱动部分动力学方程求解
利用方程序列求解法[12,14-16],从力的传递末端构件行星轮开始,逆着力的传递顺序最终达到驱动件行星架,进行栽植装置驱动部分的动力学方程求解。
(1)由式(20)求得MQ,将MQ代入式(21)、(22)求得FQx、FQy,进而由式(17)、(18)求得FB1x和FB1y。
(2)由式(14)求得MP,将MP代入式(15)、(16)求得FPx和FPy,进而由式(12)、(13)求得FA1x和FA1y。
(3)由式(9)~(11)分别求得FOx、FOy和M1。
(4)由式(28)求得ML,进而由式(24)~(26)求得FO1x、FO1y、FO1z。
3 偏心-椭圆齿轮行星轮系栽植装置动力学优化
3.1 栽植装置动力学性能要求
由于栽植装置安装在悬臂梁上,垂直方向力的变化是引起装置振动的主要因素[17-19],因此栽植装置动力学性能可通过支座垂直方向受力(太阳轮轴心y方向的力与行星架轴心y方向的力之和)情况来进行判断,包括一个作业循环中垂直方向所受作用力的峰值力和力的波动。其中峰值力的大小用一个作业循环中力的最大值和最小值之差来描述,力的波动用一个作业循环内各个位置力的方差来表示。峰值力大,说明构件受力情况不理想;力波动大,说明装置振动大、工作平稳性差。因此,理想的动力学特性要求是峰值力小,且力波动小[14]。
3.2 目标函数的建立
由栽植装置动力学性能要求可知,动力学优化时,有2个目标:峰值力小和力波动小。
设
FOy=(FOy-1,FOy-2,…,FOy-N)
FO1y=(FO1y-1,FO1y-2,…,FO1y-N)
定义栽植装置支座垂直方向峰值力函数为f1(x),波动的函数为f2(x),则
f1(x)=max(FOy+FO1y)-min(FOy+FO1y)
(29)
(30)
其中N表示将一个周期内行星架的转角等分数,分别计算不同行星架转角对应的支座垂直方向力。
根据移栽机实际作业的情况,引入权重系数,峰值力和波动方差分别赋予权重系数0.6和0.4[14],则动力学优化目标函数为
F(x)=min(0.6f1(x)+0.4f2(x))
(31)
3.3 约束条件
栽植装置满足理想栽植要求[10-11]的参数范围,作为动力学参数优化的约束条件。
3.4 优化结果
偏心-椭圆齿轮行星轮系栽植装置需优化的机构参数包括栽植嘴的初始安装角θ、两级非圆齿轮转动中心连线的夹角γ、偏心太阳轮初始相位角α3、第二中间椭圆齿轮初始相位角β6、偏心太阳轮半径R3、偏心太阳轮偏心距e3、偏心太阳轮变性系数m31、第二中间椭圆齿轮长轴A6、第二中间椭圆齿轮偏心率k6和第二中间椭圆齿轮变性系数m61,其满足理想栽植要求的机构参数优化结果为一系列非劣解[10-11],以非劣解空间中每个参数的最大值作为该参数的上限,最小值作为该参数的下限,得到该装置满足理想栽植要求的机构参数范围为65.64°≤θ≤65.91°,30.77°≤γ≤30.91°,25.23°≤α3≤25.54°,1.25°≤β6≤1.4°,30.46 mm≤R3≤31.01 mm,5.58 mm≤e3≤5.59 mm,1.45≤m31≤1.56,30.21 mm≤A6≤30.74 mm,0.03≤k6≤0.04,1.04≤m61≤1.31。
运用Matlab遗传算法工具箱中的函数寻找偏心-椭圆齿轮行星轮系栽植装置动力学优化目标函数的最小值[20],遗传算法基本参数选取如下:种群中个体的数目为40;最大遗传代数为200;变量的二进制位数为20;种群中个体选择比率为0.8;交叉概率为0.75;变异概率为0.01。得到具有最优动力学特性的机构参数为θ=65.744°、γ=30.834°、α3=25.467°、β6=1.375°、R3=30.916 mm、e3=5.583 mm、m31=1.542、A6=30.694 mm、k6=0.031、m61=1.26。
4 偏心-椭圆齿轮行星轮系栽植装置动力学试验
4.1 动力学试验测定参数
根据最优机构参数搭建偏心-椭圆齿轮行星轮系栽植装置动力学特性测试试验台,如图8所示,进行动力学特性测试。在蔬菜移栽机中,栽植装置是通过支座与移栽机相连接的。为更好地掌握栽植装置的动力学特性,采用压电式力传感器(CL-YD-3301型,测力范围为±2 000 N,过载能力120%),将其与支座固联,测定在一个工作周期中支座垂直方向受力,确定其与行星架转角之间的关系[17-18]。

图8 动力学特性测试试验台Fig.8 Test bed for measurement of dynamics characteristics
4.2 动力学试验结果与分析
栽植装置在工作转速为40 r/min时,一个工作循环中支座垂直方向受力与行星架转角关系的试验结果如图9a所示。理论分析结果如图9b所示,动力学试验和理论分析得到的支座垂直方向所受作用力的峰值力和波动方差如表1所示。
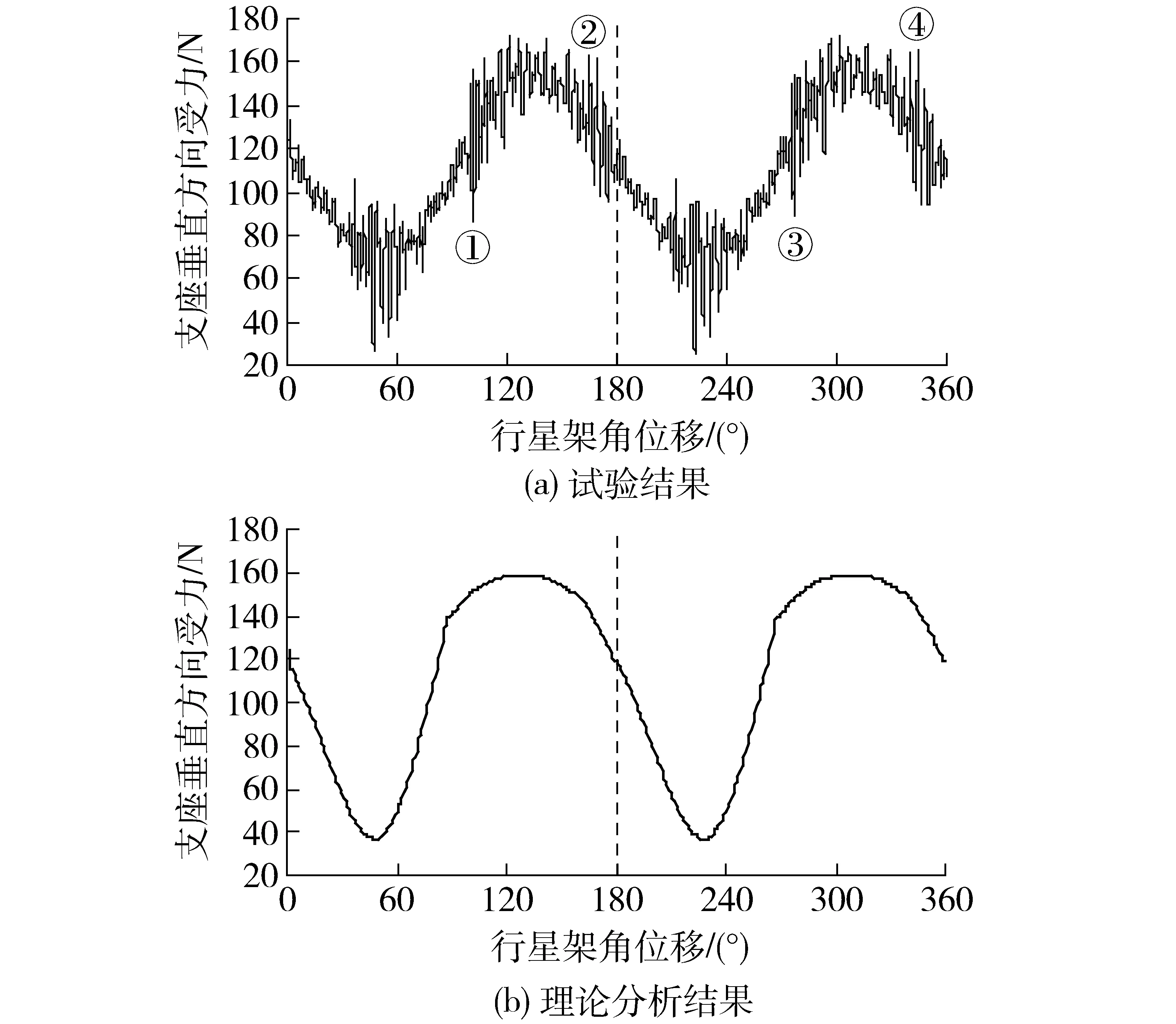
图9 支座垂直方向受力与行星架转角的关系Fig.9 Relationship between force on support in vertical direction and rotation angle of planetary carrier

垂直方向受力最大值/N最小值/N峰值力/N波动方差试验结果 171.9624.93147.031033.23理论分析结果158.9436.77122.171907.32
从图9可以看出,在一个运动周期内,栽植装置支座垂直方向受力可分为2个全等的过程(以图中虚线所示行星架转角180°为分界点,正好与栽植装置相位角相差180°的2个一样的栽植嘴相对应)。图9a和图9b的变化趋势是一致的,其中图9a的试验结果曲线出现锯齿形的波动,其主要原因是电动机输入速度不是恒定的,根据试验时的转速表显示,其速度在35~45 r/min波动;相对图9b所示的曲线,图9a的试验结果曲线出现4个明显的波动,其中位置①是下侧栽植嘴(初始位置时在下方的栽植嘴)开始闭合的位置,此时行星架转角约为100°,位置②是上侧栽植嘴(初始位置时在上方的栽植嘴)张开的位置,此时行星架转角约为160°,位置③是上侧栽植嘴闭合的位置,此时行星架转角约为280°,位置④是下侧栽植嘴张开的位置,此时行星架转角约为340°。其主要原因是试验样机端面凸轮廓线加工误差,使栽植嘴张开和闭合时滚子不能正好贴合凸轮廓线运行,造成额外冲击力。
从表1的数据可以看出,试验条件下的峰值力大于理论分析结果,这主要是因为理论上齿轮副不存在齿侧间隙,但实际上制造和安装的误差会造成齿轮副存在齿侧间隙,造成额外冲击力。而试验条件下波动方差小于理化分析结果,这是因为理论计算时将各运动部件作为纯刚体处理,而在实际运转时,各部件会发生一定程度的变形,从而吸收部分能量,而理论计算时不计入能量消耗,因此实际运转时波动相对较小。
从上面的试验结果和分析可知,所建立的动力学特性分析模型是可靠的,可为动力学特性优化提供可靠数学模型。
5 结论
(1)在建立偏心-椭圆齿轮行星轮系栽植装置动力学分析模型的基础上,以一个作业循环中支座垂直方向所受作用力的峰值力和波动最小为目标建立其动力学优化模型,以该装置满足理想栽植要求的非劣解集为约束条件,优化得到了该装置最优的机构参数,表明对栽植装置进行动力学性能优化是必要的。
(2)对基于最优机构参数搭建的偏心-椭圆齿轮行星轮系栽植装置进行动力学特性测试,测得了其在工作转速为40 r/min时一个工作循环中支座垂直方向受力与行星架转角的关系,并将其与理论分析结果进行对比,分析误差存在的原因。结果表明所建立的偏心-椭圆齿轮行星轮系栽植装置动力学分析模型是可靠的,可为其动力学优化提供可靠数学模型,同时该动力学模型也为其他类型的非圆齿轮行星轮系栽植装置动力学分析和优化提供可靠理论基础。
1 金诚谦,吴崇友,袁文胜.链夹式移栽机栽植作业质量影响因素分析[J].农业机械学报,2008,39(9):196-198.
2 刘磊,陈永成,毕新胜,等.吊篮式移栽机栽植器运动参数的研究[J].石河子大学学报:自然科学版,2008,26(4):504-506. LIU Lei, CHEN Yongcheng, BI Xinsheng, et al. Reserch on the 2ZM-2 transplanting machine with the nacelle[J]. Journal of Shihezi University: Natural Science, 2008, 26(4):504-506. (in Chinese)
3 封俊,秦贵,宋卫堂,等.移栽机的吊杯运动分析与设计准则[J].农业机械学报,2002,33(5):48-50. FENG Jun, QIN Gui, SONG Weitang, et al. The kinematic analysis and design criteria of the dibble-type transplanters[J]. Transactions of the Chinese Society for Agricultural Machinery, 2002, 33(5):48-50. (in Chinese)
4 PRASANNA KUMAR G V, RAHEMAN H.Development of a walk-behind type hand tractor powered vegetable transplanter for paper pot seedlings[J].Biosystems Engineering,2011,110(2):189-197.
5 赵雄,陈建能,杨茂祥,等.二阶自由非圆齿轮行星系钵苗移栽机取苗机构[J/OL].农业机械学报,2014,45(4):123-127. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140419&flag=1.DOI: 10.6041/j.issn.1000-1298.2014.04.019. ZHAO Xiong,CHEN Jianneng,YANG Maoxiang, et al. Seedling pick-up mechanism of planetary gear train with two-order general non-circular gears[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(4): 123-127. (in Chinese)
6 陈建能,黄前泽,赵雄,等.一种钵苗移栽机旋转式移栽装置:中国,ZL201020238733.6[P].2011-05-18.
7 陈建能,黄前泽,王英,等.钵苗移栽机非圆齿轮行星轮系栽植机构参数分析与反求[J].农业工程学报,2013,29(8):18-26. CHEN Jianneng, HUANG Qianze, WANG Ying, et al. Parametric analysis and inversion of transplanting mechanism with planetary non-circular gears for potted-seedling transplanter[J]. Transactions of the CSAE, 2013, 29(8): 18-26. (in Chinese)
8 陈建能,王英,黄前泽,等.钵苗移栽机变形椭圆齿轮行星系植苗机构优化与试验[J/OL].农业机械学报,2013,44(10):52-56,92.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20131009&flag=1.DOI: 10.6041/j.issn.1000-1298.2013.10.009. CHEN Jianneng, WANG Ying, HUANG Qianze, et al. Optimization and test of transplanting mechanism with planetary deformed elliptic gears for potted-seedling transplanter[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(10): 52-56,92. (in Chinese)
9 陈建能,黄前泽,王英,等.钵苗移栽机椭圆齿轮行星系植苗机构运动学建模与分析[J].农业工程学报,2012,28(5):6-12. CHEN Jianneng, HUANG Qianze, WANG Ying, et al. Kinematics modeling and analysis of transplanting mechanism with planetary elliptic gears for pot seedling transplanter[J]. Transactions of the CSAE, 2012, 28(5): 6-12. (in Chinese)
10 王英,陈建能,赵雄,等.非圆齿轮行星轮系传动的栽植机构参数优化与试验[J/OL] .农业机械学报,2015,46(9):85-93.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150912&flag=1.DOI: 10.6041/j.issn.1000-1298.2015.09.012. WANG Ying, CHEN Jianneng, ZHAO Xiong, et al. Parameter optimization and experiment of planting mechanism deriven by planetary non-circular gears[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 85-93. (in Chinese)
11 陈建能,章鹏华,王英,等.旋转式钵苗栽植机构多目标参数优化与试验[J/OL].农业机械学报,2015,46(5):46-53. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150508&flag=1.DOI: 10.6041/j.issn.1000-1298.2015.05.008. CHEN Jianneng, ZHANG Penghua, WANG Ying, et al. Multi-objective parameter optimization and experiment of rotary seedling planting mechanism [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 46-53. (in Chinese)
12 赵匀.机构数值分析与综合[M].北京:机械工业出版社,2005.
13 孙桓,陈作模,葛文杰.机械原理[M].北京:高等教育出版社,2006.
14 陈建能.椭圆齿轮行星系分插机构的动力性能分析、参数优化及实验验证[D].杭州:浙江大学,2004. CHEN Jianneng. Dynamics performance analysis, parameters optimization and proof for transplanting mechanism with planetary elliptic gears [D]. Hangzhou: Zhejiang University, 2004. (in Chinese)
15 王英,陈建能,周丽莎,等.步行式插秧机共轭凸轮推秧装置动力学分析与试验[J/OL].农业机械学报,2012,43(10):47-52, 100. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20121009&flag=1.DOI: 10.6041/j.issn.1000-1298.2012.10.009. WANG Ying, CHEN Jianneng, ZHOU Lisha, et al. Dynamic analysis and experiment of conjugate cam seedling-pushing device applied on walking-type rice transplanter[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(10): 47-52, 100. (in Chinese)
16 CHEN Jianneng, ZHAO Yun, YU Gaohong, et al.Establishment and verification of dynamics model of seedling-pushing device in transplanting mechanism with planetary elliptic gears[J].Transactions of the CSAE, 2003, 19(5):71-76.
17 叶秉良,李丽,俞高红,等.蔬菜钵苗旋转式取苗机构动力学分析与试验[J/OL].农业机械学报,2014,45(6):70-78. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20140612&flag=1. DOI:10.6041/j.issn.1000-1298.2014.06.012. YE Bingliang, LI Li, YU Gaohong, et al. Dynamics analysis and test of rotary pick-up mechanism for vegetable pot-seedling[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6): 70-78. (in Chinese)
18 叶秉良,朱浩,俞高红,等.旋转式水稻钵苗移栽机构动力学分析与试验[J/OL]. 农业机械学报,2016,47(5): 53-61. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160508&flag=1. DOI:10.6041/j.issn.1000-1298.2016.05.008. YE Bingliang, ZHU Hao, YU Gaohong, et al. Dynamics analysis and tests of rotary transplanting mechanism for rice pot-seedling[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(5): 53-61. (in Chinese)
19 陈建能,赵匀,李革,等.椭圆齿轮行星系分插机构动力学特性的试验[J].农业机械学报,2006,37(1):40-42, 46. CHEN Jianneng, ZHAO Yun, LI Ge, et al. Study of dynamic characteristics of transplanting mechanism with elliptic planetary gears through experiment[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(1): 40-42,46. (in Chinese)
20 雷英杰,张善文,李续武,等.Matlab遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014.
Dynamics Optimization and Experiment of Planting Device Driven by Planetary Eccentric Gears and Elliptic Gears
WANG Ying1XIA Xudong2HE Xiaojing2ZHAO Xiong2CHEN Jianneng2
(1.FacultyofMechanicalEngineeringandMechanics,NingboUniversity,Ningbo315211,China2.CollegeofMechanicalEngineeringandAutomation,ZhejiangSci-TechUniversity,Hangzhou310018,China)
Planting devices driven by double-stage planetary non-circular gear pairs can meet the requirements of ideal planting better. A total of 25 kinds of planting devices can be obtained by using gear pair composed of elliptic gear and conjugated non-circular gear, eccentric gear and conjugated non-circular gear, Pascal curve non-circular gears, Fourier curve non-circular gears or sinusoidal non-circular gears, which were used to design this type of planting device. To quickly and easily get structural parameters that can make the planting devices meet the requirements of ideal planting, kinematic multi-objective parameter optimization model was established, but the optimization results were a set of Pareto solutions. To obtain the optimal structural parameters, dynamic analysis and optimization should be implemented. So the planting device driven by eccentric gears and elliptic gears, whose first-stage planetary gear pair was composed of eccentric gear and conjugated non-circular gear and second-stage planetary gear pair was composed of elliptic gear and conjugated non-circular gear, was chosen as the research object. Its dynamic analysis model and optimization model were deduced firstly. Then dynamic optimization of this device was implemented and the optimal structural parameters were obtained. During the process of optimization, the constraint conditions were got form its Pareto solutions of kinematic optimization. A test bed for measurement of dynamics characteristics of planting device was manufactured based on the optimal parameters, and the force on the support was tested when the speed was 40 r/min. The comparison between the results of test and theoretical analysis showed that the dynamic analysis model was reliable and it was able to provide reliable mathematical model for dynamic optimization. The research also provided theoretical basis and experiment instructs for other kinds of planting devices driven by double-stage planetary non-circular gear pairs.
seedling transplanter; planetary non-circular gears; planting device; dynamics analysis; optimization; experiment
10.6041/j.issn.1000-1298.2017.01.006
2016-11-08
2016-11-27
国家自然科学基金项目(51505239)、浙江省重大科技专项重点农业项目(2015C02004)、浙江省自然科学基金项目(LQ15E050003、LY15E050026)和宁波市自然科学基金项目(2015A610099)
王英(1989—),女,讲师,博士,主要从事机构分析与综合研究,E-mail: wangying5@nbu.edu.cn
陈建能(1972—),男,教授,博士生导师,主要从事现代农业装备与技术研究,E-mail: jiannengchen@zstu.edu.cn
S223.9
A
1000-1298(2017)01-0038-09

