浆翼式力矩马达反馈特性研究
孟 彬 申屠胜男 林 琼 阮 健
(浙江工业大学特种装备制造与先进加工技术教育部重点实验室, 杭州 310014)
浆翼式力矩马达反馈特性研究
孟 彬 申屠胜男 林 琼 阮 健
(浙江工业大学特种装备制造与先进加工技术教育部重点实验室, 杭州 310014)
针对现有的位置直接反馈式二维(2D)伺服阀的液压伺服螺旋结构复杂和加工昂贵的不足,提出一种具有反馈机能的浆翼式力矩马达,将其作为电-机械转换接口与阀芯相连而构成结构简单、加工成本低的力反馈式二维(2D)伺服阀。加工了3种不同浆翼倾角的马达样机并搭建了实验台架,分别采用磁路解析、有限元模拟和实验研究的方法研究了该马达的反馈力矩与衔铁轴向位移之间的特性关系。实验结果和模拟结果基本相符,显示该马达的反馈力矩-位移特性曲线呈线性关系,且幅值随着衔铁位移增加而增大;对比不同倾角的特性曲线可以得知,增大浆翼倾角是增加反馈力矩的有效手段。
力矩马达; 浆翼; 反馈特性; 二维阀; 力反馈
引言
对于比例/伺服控制元件而言,液动力是阻碍阀芯运动的主要阻力之一。而受到磁饱和限制,电-机械转换器输出的电磁力/力矩通常较小,难以有效克服液动力而得到满意的控制特性[1-3]。为解决该问题,人们采用先导式控制的方法,将阀设计成导控式的多级结构。在电液控制技术的发展历程中,先后出现过喷嘴挡板先导级、射流管先导级和滑阀先导级,应用于大流量比例/伺服阀中,取得了较为满意的效果[4]。
滑阀阀芯具有径向旋转和轴向移动两个自由度,且不相互干涉,因而可以分别实现导控级和功率级的功能[5],这就是基于阀芯双自由度的二维流量放大机构的设计思想,但如何通过合理的结构设计实现其导控和功率级的一体化,则是使用这个原理时必须攻克的难点。阮健等[6-8]基于该原理提出了一种位置直接反馈式二维(2D)电液伺服阀,其实现阀芯旋转与轴向位移转换的结构类似于机械的螺旋运动,因此被称为液压伺服螺旋机构。该阀动态响应快,抗污染能力好[9-11]。但该阀液压伺服螺旋的内螺旋槽需要进口的三轴以上电火花机床才能加工,且加工效率较低,精度难于保证。
为改进现有的位置直接反馈式二维(2D)伺服阀,本文提出一种具有反馈机能的浆翼式力矩马达,阐述浆翼式力矩马达的工作原理,加工3种不同浆翼倾角的马达样机并搭建实验台架,分别采用磁路解析、有限元模拟和实验研究的方法研究该马达的反馈力矩和衔铁轴向位移以及不同浆翼倾角之间的特性关系。
1 结构与工作原理
电-机械转换器的性能对于电液控制元件而言具有决定性的影响作用[12-15]。普通的力矩马达是喷嘴挡板伺服阀和射流管伺服阀常用的电-机械转换元件,其输出力矩大,动态响应高,马达衔铁为平翼结构,其只能绕旋转轴转动,并不具备反馈功能[16-17]。本文提出的浆翼式力矩马达,其结构示意图和剖面磁路图分别如图1和图2所示,主要包含轭铁部件、衔铁、磁钢、励磁线圈及螺钉等。上下轭铁及衔铁均以软磁材料为导磁体,磁钢选用钕铁硼稀土永磁,左右2个磁钢对称放置于上下轭铁之间以产生极化磁场;2个励磁线圈则置于上下轭铁内侧以产生控制磁场。为实现反馈功能,衔铁的左右翼面、上下轭铁的极靴表面都设计有浆翼状的倾角,即以垂直于水平面、竖直向上的轴为中心轴,衔铁左右翼面和上下轭铁的极靴表面均呈以该轴为中心轴的180°阵列特征,以此形成左右各2个相同高度的倾斜工作气隙,该马达也因此被称为浆翼力矩马达。

图1 浆翼式力矩马达结构示意图Fig.1 Structure schematic of paddle wing torque motor1.上轭铁 2.左磁钢 3.下轭铁 4.左线圈 5.右线圈 6.衔铁 7.右磁钢 8.螺钉
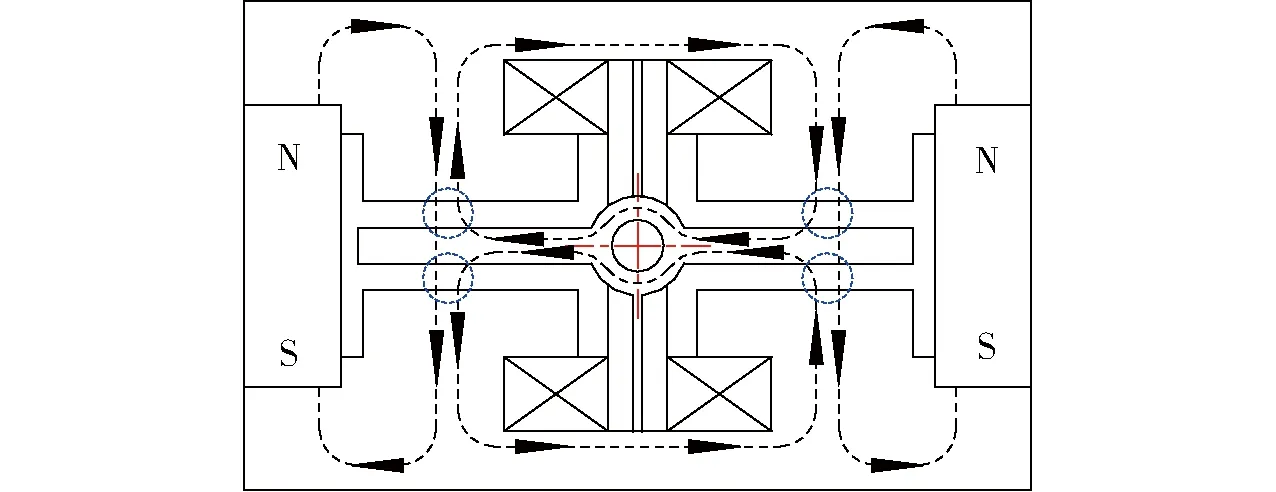
图2 浆翼式力矩马达剖面磁路图Fig.2 Sectional magnetic circuit diagram of paddle wing torque motor
图3所示为该马达与阀芯直接相连时构成的力反馈式二维(2D)伺服阀的示意图,其为利用阀芯的旋转和直线双运动自由度设计的二级流量阀,它由阀芯、阀套和阀体等构成。阀芯左侧为敏感腔,靠近敏感腔的阀芯台肩上开有2对轴对称的矩形高低压口,相应位置上的阀套开设有2条轴对称的感受通道窗口,其左端和敏感腔相通,右端上下侧与阀芯高低压口之间形成由阀芯转动控制的2个节流口,并串联形成液压阻力半桥,以此控制敏感腔内的压力。阀芯右腔则经阀芯杆内通道和高压孔与进油口相通,其压力为系统压力,右腔面积为环形面积,在设计时保证其为左敏感腔的一半。而从阀右腔伸出的阀芯杆则与安装于其右端的桨翼式力矩马达的衔铁固联,马达线圈不通电时由弹簧杆支承衔铁并保持4个工作气隙相同。
当马达通电时,衔铁驱动阀芯作顺时针的转动(从左向右看),直到输出力矩和弹簧杆的阻力矩相等的平衡位置,如图3a所示;此时衔铁工作气隙高度发生变化(g1和g2,g1>g,g2
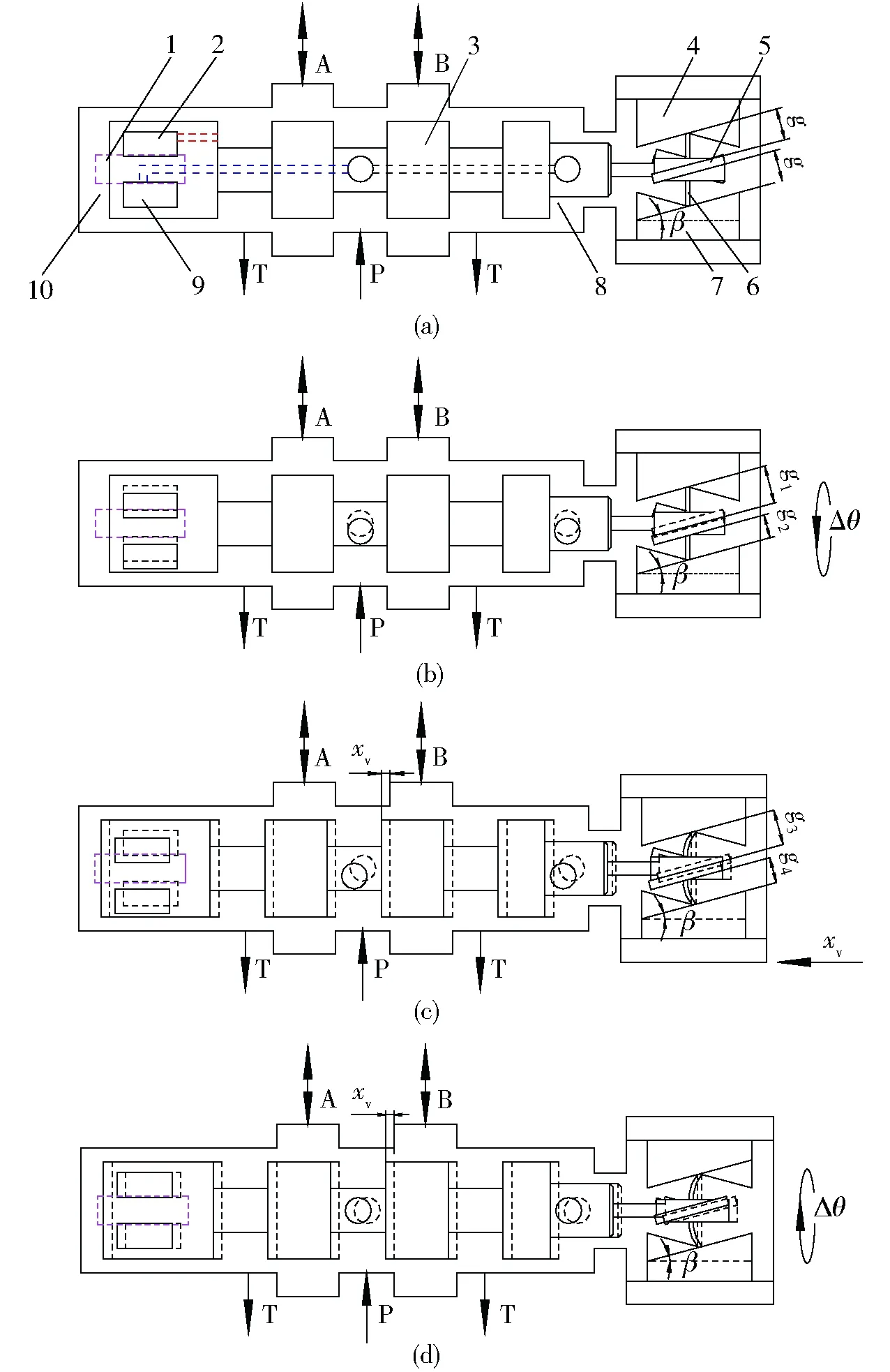
图3 力反馈式二维(2D)伺服阀示意图Fig.3 Schematics of force feedback 2D servo valve1.感受通道窗口 2.低压口 3.阀芯 4.上轭铁 5.衔铁 6.弹簧杆 7.下轭铁 8.高压腔 9.高压口 10.敏感腔
2 磁路解析
磁路解析法的精度不及有限元模拟,但是其可以通过建立集总参数模型,以解析方程式的形式表达力矩马达的静动态特性,物理意义明确,并可为后续精确的电磁场数值模拟提供参考。浆翼式力矩马达的反馈力矩-位移特性是指在衔铁转角不变时,马达的反馈力矩和衔铁轴向位移之间的关系。假设软磁材料的磁阻可以忽略不计。只考虑4个工作气隙的磁阻,则力矩马达的磁路可以用图4所示的等效磁路图来表示。
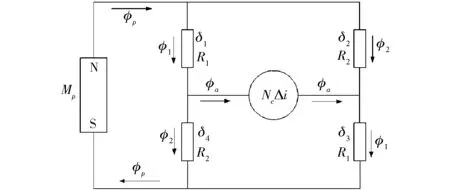
图4 浆翼式力矩马达等效磁路图Fig.4 Schematic of equivalent magnetic circuit of paddle wing torque motor
当衔铁处于中位且轴向无位移时,每个工作气隙磁阻可以表示为
(1)
式中lg——衔铁在中位时每个气隙的长度Ag——磁极面的面积μ0——空气导磁率
当衔铁偏离中位且轴向无位移时,每个工作气隙的磁阻可以表示为
(2)
(3)
式中Ri——气隙δi的磁阻,i=1,2,3,4x——衔铁端部偏离中心的位移
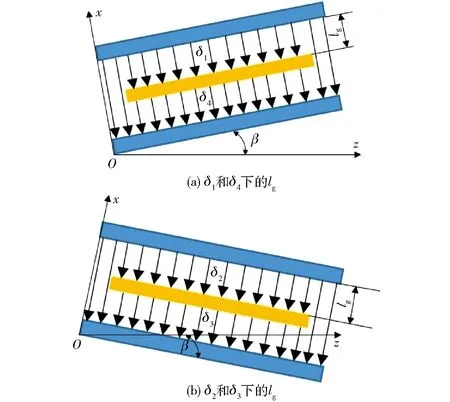
图5 气隙长度lg沿x轴和z轴方向的变化Fig.5 Variations of lg along direction of axes x and z
结合图1的结构示意图,定义衔铁轴向移动的方向为z轴,与上下轭铁垂直的方向为x轴,可以用图5来表示气隙长度lg沿x轴和z轴方向的变化。当轴向位移不为零时,每个工作气隙的磁阻可以表示为
(4)
(5)
式中z——衔铁轴向位移β——浆翼力矩马达倾角
由于磁路都是对称的桥式磁路,通过对角线气隙的磁通是相等的,对包含气隙δ1和δ3、极化磁动势Mp和控制磁动势NcΔi的闭合回路应用磁路的基尔霍夫第二定律,可得气隙δ1和δ3下的合成磁通为
(6)
(7)
式中Mp——磁钢产生的极化磁动势Nc——控制线圈的匝数NcΔi——控制电流产生的控制磁动势
用衔铁在中位时的极化磁通φg和控制磁通φc来表示Mp和NcΔi,可以得到
(8)
(9)
将式(8)、(9)代入式(6)、(7)可得
(10)
(11)
衔铁在磁场中所受电磁吸力按照Maxwell公式计算[18],可以写为
(12)
式中F——电磁吸力φ——气隙中磁通
由控制磁通和极化磁通相互作用在衔铁上产生的电磁力矩为
Td=2a(F1-F4)
(13)
式中a——衔铁转动中心到磁极面中心距离F1、F4——气隙δ1和δ4处的电磁吸力
考虑到马达作为伺服阀的电-机械转换器,无论是衔铁轴向位移(等于阀芯开口)还是衔铁转角均非常小,可得
(14)
将式(1)~(12)代入式(13)并结合式(14),可以得到马达总的电磁力矩为
Td=KtΔi+Kmrθ-Kmlz
(15)
其中
(16)
(17)
(18)
式中Kt——马达的中位电磁力矩系数Kmr——马达的中位旋转磁弹簧刚度Kml——马达的中位直动磁弹簧刚度θ——衔铁转角
可以看到在式(15)中,马达的输出力矩主要由3项组成,其中KtΔi项是衔铁在中位时,由控制电流Δi产生的电磁力矩,称为中位电磁力矩,这也是驱动阀芯旋转的主力矩;Kmrθ项是由于衔铁绕z轴旋转时产生的附加电磁力矩,其效果是使衔铁进一步偏离中位,类似于扭簧的特性,称为电磁扭转弹簧力矩,由于其为正磁弹簧刚度,幅值与转角呈正比,因此马达在实际使用中需要外加扭转弹性元件以避免衔铁被吸附到极靴上;Kmlz项则是衔铁沿着z轴移动时产生的力矩,称为电磁直动弹簧力矩,因其为负磁弹簧刚度,可以用作反馈力矩构成力-位移闭环的负反馈回路。此外,从式(18)可以看出Kml与浆翼倾角β的正弦函数呈正比,因此增加β是增大反馈力矩的有效手段。
上述的解析公式推导证明了浆翼式力矩马达中反馈力矩的存在。值得一提的是,经典的电液伺服控制教材中对普通力矩马达的输出力矩表达式有明确表述[19],将之与式(15)对比可以发现,普通力矩马达由于没有浆翼结构,其力矩表达式只包含KtΔi项和Kmrθ项,而没有Kmlz项,即不具备反馈功能。
3 有限元模拟
为精确预测马达的反馈力矩,在前述磁路解析的基础上,需要对其做反馈力矩-位移特性的有限元数值模拟,由此在Ansoft/Maxwell软件里建立了马达的三维电磁场有限元模型。图6所示为衔铁位移分别为0 mm和1.8 mm时,模拟得到的马达磁场云图(为清晰起见,去掉了线圈、保持架和磁钢),可以看到当没有轴向位移时,衔铁处于中位,此时整个磁路的磁阻最大,上下轭铁和衔铁的磁场强度呈现一种对称均匀的状态,马达不产生反馈力矩;而当衔铁轴向移动时,整个磁路的磁阻减小,磁通增大,马达产生反馈力矩,衔铁与上下轭铁趋近的一侧翼面磁场强度增强,与其远离的一侧翼面则减弱,对于轭铁而言,情况同样如此。可见其磁场分布与前述的工作原理是一致的。
Maxwell软件内置有力矩/力计算功能[20],因此通过其CAD界面改变衔铁轴向坐标后,便可以采用三维静磁场模拟计算出该位置的反馈力矩。图7所示为模拟得到的在磁钢单独励磁情况下,衔铁轴向位移±1.8 mm范围内的3种不同浆翼倾角(9°、12°和15°)的反馈力矩-位移特性。可以看到其特性曲线呈线性关系,且相对于零位而言,衔铁正负行程内的力矩幅值基本是对称的。衔铁在中位时由于4个气隙高度相等,因此无反馈力矩输出,随着衔铁(被阀芯带着)轴向移动,反馈力矩也随着线性增加;另外,对比3种倾角的曲线,可以看到反馈力矩的幅值随着浆翼倾角的增加而增大,在阀芯位移为1.8 mm时,力矩幅值分别达0.102 N·m、0.144 N·m和0.175 N·m。
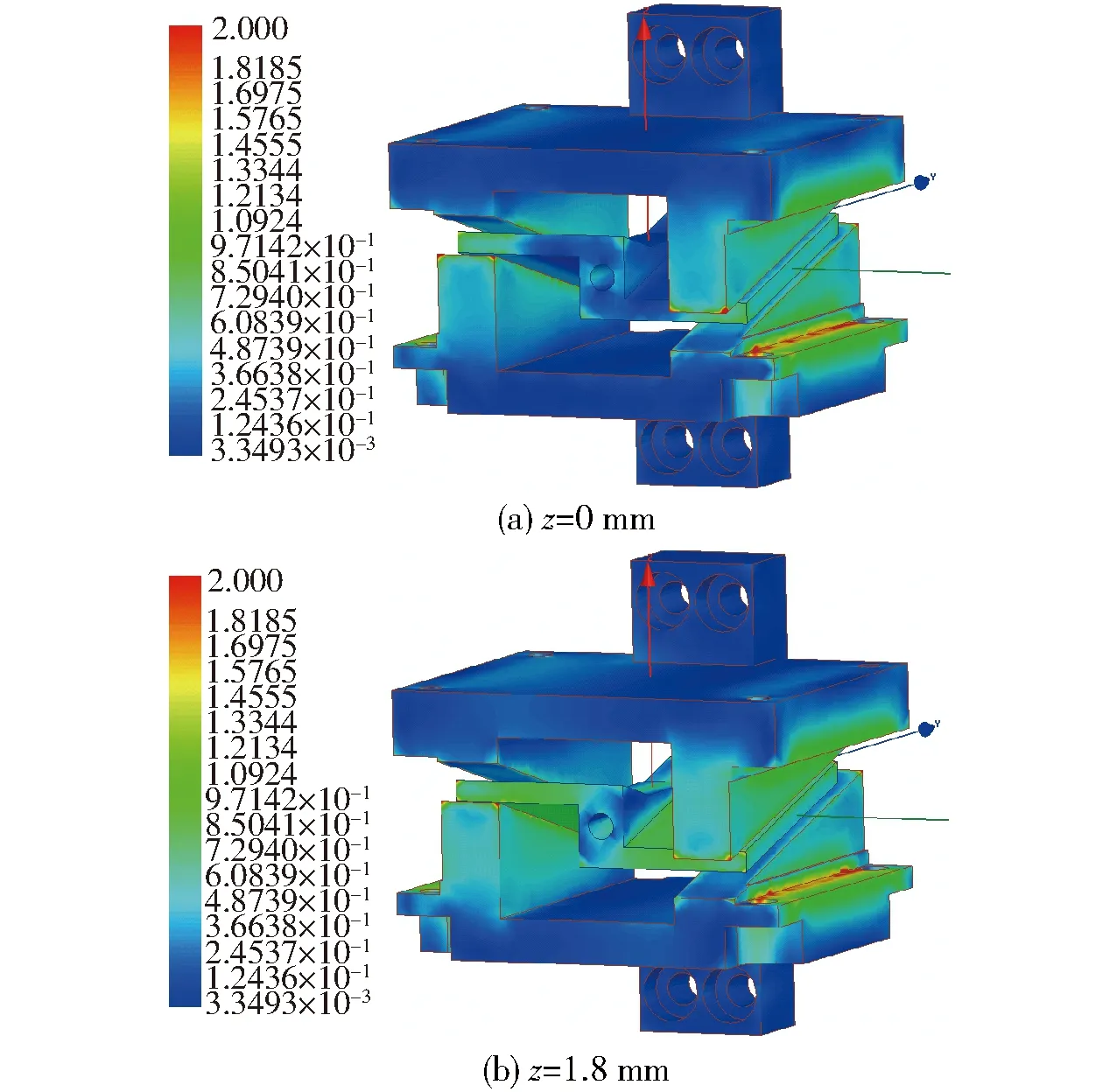
图6 浆翼式力矩马达磁场云图Fig.6 Magnetic field contours of paddle wing torque motor
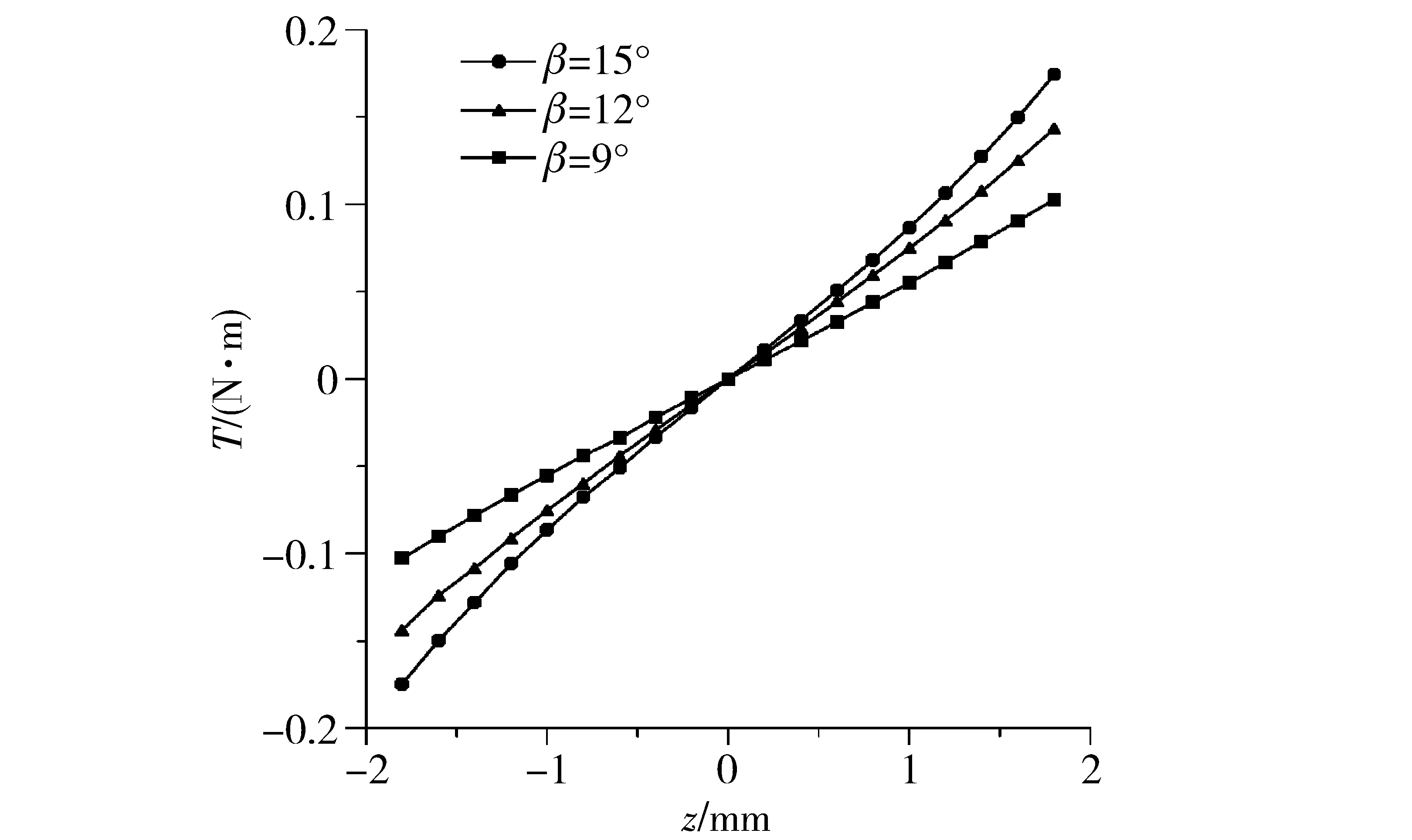
图7 有限元模拟的反馈力矩-位移特性Fig.7Simulated feedback torque-displacement characteristics
4 实验
前述磁路解析及有限元模拟的正确性需要实验的验证。考虑到浆翼式力矩马达的衔铁同时涉及到双自由度作动,按传统测试方法的思路,衔铁既要移动又要转动,极易引起干涉而无法达到测试要求。本文提出了一种通过移动轭铁来改变其与衔铁之间的位置,从而测得马达反馈力矩与衔铁位移之间关系的方法,设计的实验台架如图8所示。该台架主要由底座、连接板、微调直动台、联轴器、扭矩传感器和固定块组成。衔铁轴以不导磁不锈钢制成,和衔铁过盈连接后通过轴承将衔铁支撑在b板和c板之间;衔铁轴一端悬空,另一端通过联轴器,待调节好马达零位后与扭矩传感器的输入轴连接,扭矩传感器的输出轴通过联轴器和固定块连接,两者则分别安装在d板和e板上。马达的上下轭铁和磁钢等组合后整体固定在a板上,a板再与微调直动台的上表面固连。最后b~e板和微调直动台则固连在底座上。微调直动台可通过手调(粗调和微调)方式使得马达轭铁得到微小直线运动,其精度可达到±0.1 mm。测试时手动调节微调直动台的旋杆,使得上下轭铁连同a板相对于衔铁发生直线移动并记录移动距离,马达的反馈电磁力矩则由扭矩传感器读出,如此则得到马达的反馈力矩-衔铁位移特性。上述的测试方法,使得轭铁和衔铁各自负责单个自由度的运动,简化了测试流程,装置的成本也较低。此外,为研究浆翼倾角对反馈力矩的影响,分别加工了β为9°、12°和15°的3种马达样机,如图9所示。为调节马达零位从而使得测试时4个工作气隙的高度相等,加工了厚度等同于气隙高度的高精度垫片,测试时先将马达松开,在气隙中塞入垫片以使得衔铁保持在中位,随后按上述步骤连接台架,完成后取出垫片。
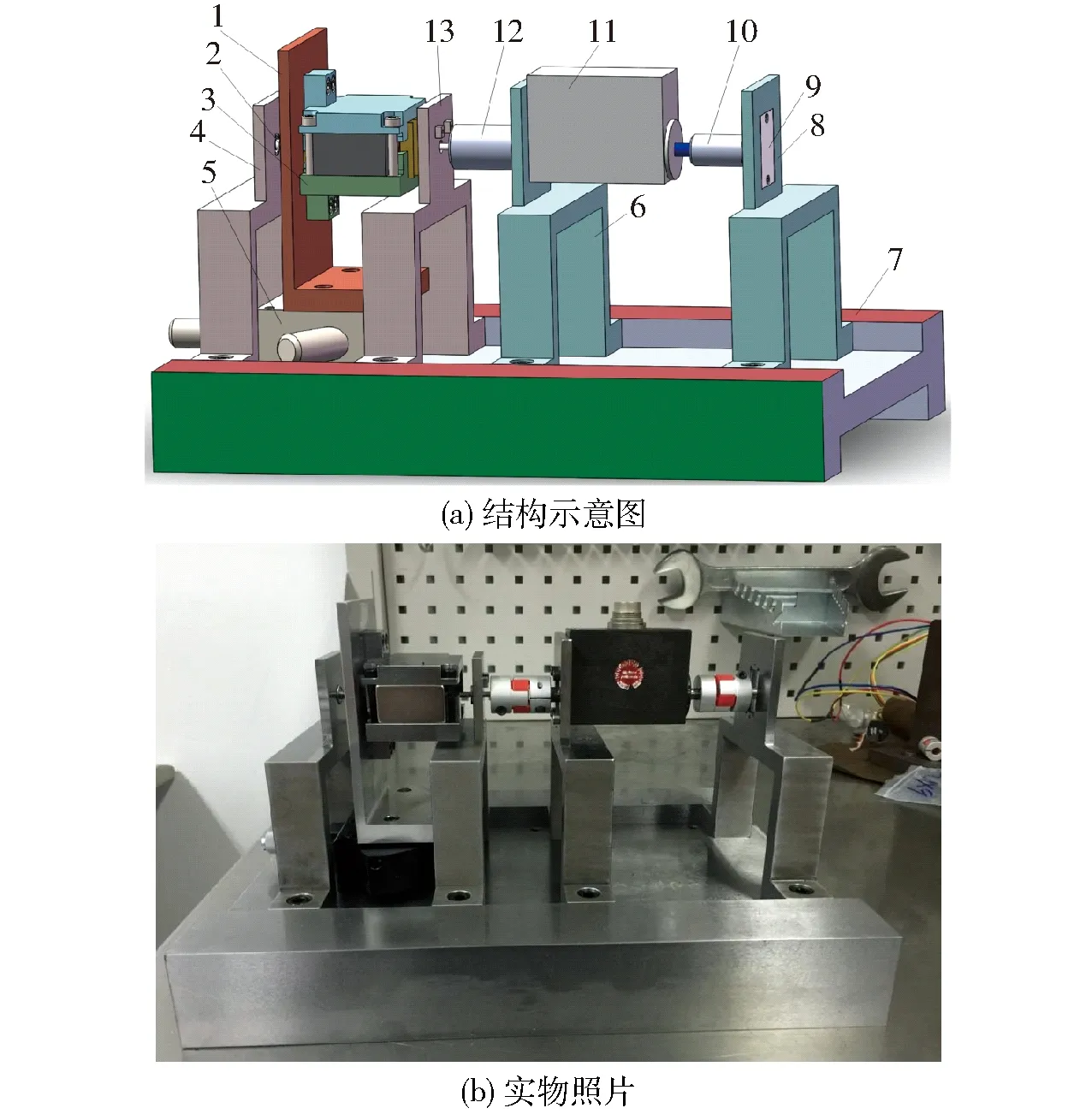
图8 马达反馈力矩的测试台架 Fig.8 Test rig of motor’s feedback torque1.a板 2.衔铁轴 3.马达样机 4.b板 5.微调直动台 6.d板 7.底座 8.e板 9.固定块 10、12.联轴器 11.扭矩传感器 13.c板

图9 3种不同倾角的马达样机Fig.9 Three types of torque motor prototypes with different inclined angles
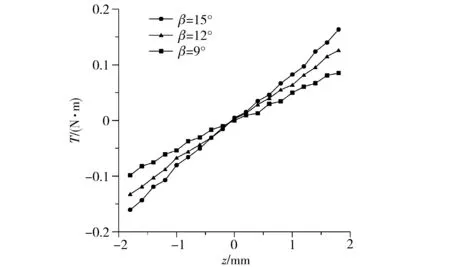
图10 实测的反馈力矩-位移特性Fig.10 Measured feedback torque-displacement characteristics
图10所示为实测得到的在磁钢单独励磁情况下,衔铁轴向位移±1.8 mm范围内,3种不同浆翼倾角的马达反馈力矩-位移特性,在阀芯位移为1.8 mm时,力矩幅值分别达0.098 N·m、0.132 N·m和 0.16 N·m,力矩幅值随着浆翼倾角的增加而增大。实验结果比有限元模拟值略微偏小,其原因可能是有限元自带的材料特性参数相比实际值有一定的差异,且实验过程中存在各种静摩擦和动摩擦。另外,由于马达衔铁的零位设定以及机械加工有一定误差,导致力矩曲线相对于零位而言,存在轻微不对称。
马达反馈过程中的动态响应也是其主要特性之一,但考虑到实际工作过程中阀芯由液压力驱动,其轴向位移的发生可以认为是瞬时的。故在马达的单独研究中,在没有滞后的情况下给出其输入信号,对于实验台架搭建是非常困难的,理想的方式是等马达和阀体连接后,直接测试整个阀的动态响应。现阶段而言,在衔铁质量一定的情况下,反馈力矩和马达的动态响应是呈正比的,因此可以将反馈力矩作为其动态响应的参考。
5 结论
(1)提出了一种具有反馈机能的浆翼式力矩马达,理论分析和实验研究证明其反馈力矩-位移特性呈线性关系,力矩幅值随位移增加而增加,浆翼倾角为15°时最大反馈力矩达到0.16 N·m。将其作为电-机械转换接口与滑阀阀芯相连可构成结构简单、加工成本低的力反馈式二维伺服阀。
(2)加工了浆翼倾角β分别为9°、12°和15°的3种马达样机。理论和实验研究均表明,马达反馈力矩的幅值随着浆翼倾角的增加而增大,因此β是控制反馈力矩的关键参数,在具体结构设计时应该将β设计得尽可能大以增加反馈力矩。但β过大会影响励磁线圈漆包线的缠绕体积,从而减小线圈匝数,因此需要折中选择。
1 成大先. 机械设计手册单行本:液压控制[M] . 北京: 化学工业出版社, 2010.
2 吴根茂, 邱敏秀, 王庆丰,等. 新编实用电液比例技术[M] . 杭州: 浙江大学出版社, 2006.
3 DING C, DING F, ZHOU X, et al.Novel pressure-resistant oil-immersed proportional actuator for electrohydraulic proportional control valve [J].ASME Journal of Mechanical Design, 2013, 135(12):125001-125001-5.
4 雷天觉. 新编液压工程手册[M]. 北京: 北京理工大学出版社,1998.
5 阮健. 电液直接数字控制技术[M].杭州: 浙江大学出版社, 2000.
6 阮健, 裴翔, 李胜. 2D数字换向阀[J]. 机械工程学报, 2000, 36(3): 65-68. RUAN J, PEI X, LI S. 2D electro-hydraulic digital directional valve [J].Journal of Mechanical Engineering, 2000, 36(3): 65-68. (in Chinese)
7 RUAN J, BURTON R, UKRAINETZ P. An investigation into the characteristic of a two dimensional “2D” flow control valve [J]. ASME Journal of Dynamic Systems, Measurement and Control, 2002,124(1): 214-220.
8 阮健, 李胜, 裴翔,等. 数字阀的分级控制及非线性[J]. 机械工程学报, 2005, 41(11): 91-97. RUAN J, LI S, PEI X, et al. Stage control and nonlinearites of digital valves [J].Chinese Journal of Mechanical Engineering, 2005, 41(11): 91-97.(in Chinese)
9 李胜,阮健,孟彬. 二维电液比例换向阀动态特性及稳定性分析[J].机械工程学报, 2016, 52(2):202-212. LI S, RUAN J, MENG B. Two-dimensional (2D) electro-hydraulic proportional directional valve [J].Journal of Mechanical Engineering, 2016, 52(2):202-212. (in Chinese)
10 刘国文, 阮健, 李胜, 等. 2D电液比例换向阀阀芯卡紧力分析[J]. 中国机械工程, 2015, 26(15):1995-1999. LIU G W, RUAN J, LI S, et al. Analysis of spool cliping force for 2D electro-hydraulic proportional directional valve [J].China Mechanical Engineering, 2015, 26(15):1995-1999.(in Chinese)
11 REN Y, RUAN J. Regulating characteristics of an electro-hydraulic vibrator multiply controlled by the combination of a two-dimensional valve and a standard servo valve [J]. Proc. IMechE, Part C: Journal of Mechanical Engineering Science, 2013, 227(12):2707-2723.
12 孟彬, 阮健, 李胜. 新型阀用耐高压旋转电磁铁特性研究 [J/OL]. 农业机械学报,2012, 43(12): 240-245, 256. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20121243&journal_id=jcsam DOI:10.6041/j.issn.1000-1298.2012.12.043. MENG B, RUAN J, LI S. Research on the characteristics of novel electromagnet with high pressure resistance for valve [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(12): 240-245, 256.(in Chinese)
13 满军. 耐高压高速开关电-机械转换器关键技术研究 [D]. 杭州: 浙江大学, 2011. MAN J. Research on key technology of high-pressure high-speed on-off electro-mechanical converter[D]. Hangzhou: Zhejiang University, 2011.(in Chinese)
14 孟彬, 林琼, 阮健. 单相对称磁路湿式力矩马达研究 [J/OL]. 农业机械学报,2016, 47(9): 406-412. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160954&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2016.09.054. MENG B, LIN Q, RUAN J. Research on torque motor with high pressure resistance based on symmetrical magnetic circuit with single phase excitation [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(9): 406-412.(in Chinese)
15 崔剑,丁凡,李其朋,等.电液伺服转阀耐高压双向旋转比例电磁铁[J].机械工程学报,2008,44(9):230-235. CUI J, DING F, LI Q P, et al. High-pressure bi-directional rotary proportional solenoid for rotary servo valve [J].Chinese Journal of Mechanical Engineering, 2008, 44(9): 230-235.(in Chinese)
16 赵斌. 基于MATLAB的力矩马达的非线性数学建模 [J] . 煤矿机械, 2010, 31(7): 45-46. ZHAO B. Torque motor based on MATLAB mathematical modeling of non-linear [J]. Coal Mine Machinery, 2010, 31(7): 45-46.(in Chinese)
17 李松晶, 鲍文. 磁流体对伺服阀力矩马达动态特性的影响[J]. 机械工程学报, 2008, 44(12): 137-142. LI S J, BAO W. Influence on dynamic characteristics of a hydraulic servo-valve torque motor due to magnetic fluids [J]. Chinese Journal of Mechanical Engineering, 2008, 44(12): 137-142.(in Chinese)
18 王宝龄. 电磁电器设计基础[M]. 北京: 国防工业出版社, 1989.
19 MERRITT H E. 液压控制系统 [M]. 陈燕庆,译. 北京: 科学出版社,1976.
20 刘慧娟, 上官明珠, 张颖超, 等. Ansoft Maxell 13电机电磁场实例分析[M]. 北京: 国防工业出版社,2014.
Feedback Characteristics of Paddle Wing Torque Motor
MENG Bin SHENTU Shengnan LIN Qiong RUAN Jian
(KeyLaboratoryofSpecialPurposeEquipmentandAdvancedProcessingTechnology,MinistryofEducation,ZhejiangUniversityofTechnology,Hangzhou310014,China)
Hydraulic valves were designed with two dimensional (2D) concept uniquely integrated pilot stage and power stage into single spool by taking advantage of both translational and rotary degrees of freedom. It was featured with simple structure, excellent anti-pollution capability, high ratio of power to weight and fast dynamic response, which attracted considerable attention in several areas of modern industry. In order to solve the problem that hydraulic servo screw of direct position feedback 2D servo valve had deficiency of complicated structure and high manufacturing cost,a novel paddle wing torque motor with feedback function was proposed. The motor could be used as electro-mechanical converter and directly connected with spool to constitute a novel force feedback 2D servo valve with simple structure and low manufacturing cost, which was suitable for civil servo valve application. Three types of prototype motors with different inclined angles of paddle wing were manufactured and the test rig was built. The relationships between feedback torque and armature displacement were studied by using methods of magnetic circuit analysis, FEM simulation and experiments. The experimental results were agreed with the simulated results. It was indicated the characteristics between feedback torque and armature displacement were close to linear relationship and its amplitude was raised with the increase of displacement, whose magnitudes reached about 0.098 N·m, 0.132 N·m and 0.16 N·m with paddle wing’s inclined angles of 9°, 12°and 15°, respectively. It was proved that increasing inclined angle was an effective approach to increase feedback torque.
torque motor; paddle wing; feedback characteristics; 2D valve; force feedback
10.6041/j.issn.1000-1298.2017.01.048
2016-10-01
2016-11-09
国家自然科学基金项目(51405443)、浙江省自然科学基金项目(LY14E050007)和浙江省科技厅公益性项目(2016C31G2020039)
孟彬(1979—),男,副教授,博士,主要从事电液伺服控制研究,E-mail: bin_meng@zjut.edu.cn
TH137.5
A
1000-1298(2017)01-0361-07

