基于引导人工蜂群算法的3-RPS并联机构正解优化

毛冰滟 谢志江 吴小勇 袁岳军

(重庆大学机械传动国家重点实验室， 重庆 400044)

基于引导人工蜂群算法的3-RPS并联机构正解优化

毛冰滟 谢志江 吴小勇 袁岳军

(重庆大学机械传动国家重点实验室， 重庆 400044)

提出了一种求解3-RPS并联机构正解优化的快速数值解算法，采用数值优化方式将正解转换为最小化问题。针对3-RPS并联机构位姿正解优化，采用数值法建立该并联运动平台正解方程，其实质为带约束的多目标非线性方程组。建立判定方程实现方程组单目标优化，采用引导人工蜂群算法进行最小值优化求解。该算法既利用了基本人工蜂群算法中邻近蜜蜂交换蜜源信息的方式，又采用全局最优蜜蜂引导所有蜜蜂往更优蜜源处移动，更快速地搜索到最优蜜源位置。通过求解3-RPS正解数值解优化仿真算例分析，对比改进蚁群算法和基本人工蜂群算法，结果表明引导人工蜂群算法是高精度高速求解并联运动平台正解优化的一种有效方法。

并联机构； 人工蜂群算法； 运动学正解

引言

与串联机器人相比，并联机构具有高承载能力、高刚度、高精度等特点[1-2]。为达到运动精度高、可达精度小，机构的综合问题分析在于运动学求解优化，并联机构的运动学优化关键在于机构正解，即已知驱动得到位置和姿态[3-5]。

并联机构的运动学正解包含一组复杂的多目标耦合非线性方程组，传统采用的方式有数值法和解析法。任文博等[6-7]得到并联机构的封闭解析解，需要根据机构的结构特点进行判断，效率低，计算量大。数值法通常采用Newton-Raphson法进行迭代求解[8-9]，需计算雅可比矩阵及其逆矩阵，计算工作量大，结构受初值影响，计算精度达不到要求[8-11]。

近年来，智能优化算法发展迅速，如粒子群算法(Particle swarm optimization, PSO)[12-15]、遗传算法(Genetic algorithm, GA)[16]、连续蚁群算法(Ant colony algorithm, ACO)[17]等在机器人运动学求解上得到了应用。粒子群算法运算速度快，算法易于应用，但全局寻优性差，容易陷入局部最优值；遗传算法全局并行搜索，但常规的算法有收敛速度慢及早熟的缺点；连续蚁群算法为群智能算法模式，但运行速度慢。人工蜂群算法(Artificial bee colony, ABC)[18-25]仿生于蜜蜂群体采蜜时各个蜂种之间的配合，以找到最优采蜜位置。算法控制参数少，全局寻优性好，收敛速度快，具有非常好的优化搜索特性，可以有效地解决实际工程问题。利用改进的引导人工蜂群算法(Global-best artificial bee colony, GABC)，通过利用全局最优蜜蜂进行引导学习，带领全部蜜蜂向更优蜜源移动，加快算法收敛速度。

本文对3-RPS并联运动平台进行运动学分析，将运动学正解多目标非线性方程组规划问题转换为单目标优化，建立判定方程。采用人工蜂群算法以及改进的引导人工蜂群算法进行评定方程优化求解。

1 并联机构运动学分析

1.1 运动学逆解

图1为3-RPS并联机构结构简图。该机构是由上、下平台以及连接两平台的3个支链组成。上平台为运动平台，能实现3-RPS的3个自由度，下平台为固定平台，位置保持不变。支链从下往上由转动副(R副)、移动副(P副)和球副(S副)组成，转动副与固定平台连接且采用等边三角形的布置方式，球副与运动平台连接，布置方式与转动副一一对应。3条支链的长度可通过移动副的伸长缩短进行改变，从而使得运动平台位置和姿态改变。

图1 3-RPS并联机构结构简图Fig.1 Structure sketch of 3-RPS parallel manipulator

以右手定则在固定平台中心建立固定坐标系OXYZ，X轴指向转动副中心A1，Z轴垂直固定平台平面向上。在运动平台上相应的建立动坐标系O1X1Y1Z1，X1轴指向球副中心B1，Z1轴垂直运动平台向上。固定坐标系不变，该平台可实现3个自由度为绕X轴和Y轴方向的转动，以及沿Z轴方向的移动。

由机构的封闭矢量可得

LAiBi=RLO1Bi+P-LOAi(i=1,2,3)

(1)

其中

(2)

式中R——动坐标系到定坐标系的Z-Y-X欧拉旋转变换矩阵

P——动坐标系到定坐标系的位置变换矩阵

α、β、γ——绕X轴、Y轴、Z轴的转动角度

xe、ye、ze——绕X轴、Y轴、Z轴的移动距离

其中sα=sinα，cα=cosα，以此类推。

根据机构的几何关系可以确定A点和B点分别在定坐标系和动坐标系系中的位置，即

(3)

其中

式中ra——转动副所在平台半径rb——球副所在平台半径

根据并联机构实际的装配关系可知，转动副R的轴线ei与移动副P的移动方向保持垂直，则可以得到运动学约束方程

(RLO1Bi+P-LOAi)Tei=0

(4)

则可以得到3个转动副R的轴线向量为

(5)

通过式(3)～(5)可得到xe、ye、γ关于ze、α、β的表达式

(6)

式(6)为该并联机构的运动学约束方程。在带约束情况下求该三自由度并联机构的位置正解，能够得到该机构的唯一驱动。将式(6)代入式(1)中，使得在逆解的非线性方程组中只含有代表机构位置和姿态的3个自由度ze、α、β。从而可以得到ze、α、β表示向量LAiBi。

通过式(7)～(9)可得，机构实现3个自由度的驱动为移动副的驱动位移，则机构逆解为

(7)

(8)

(9)

(10)

1.2 运动学正解多目标非线性模型优化

机构正解为已知驱动位移di的情况下得到机构的位姿α、β、ze。在得到机构逆解的情况下，正解的本质在于求解一组隐式非线性方程组，即

di-fi(α,β,ze)=0 (i=1,2,3)

(11)

采用权和法将该非线性方程组转换为单目标线性规划问题，其实质为带约束的多目标非线性方程优化，转换为最小化问题，则

(12)

因此得到该并联运动平台数值正解的判定方程为

(13)

2 人工蜂群算法

2.1 基本人工蜂群算法

蜜蜂为群居动物，在群体中不同的蜜蜂有不同的角色和任务。单个蜜蜂行为简单，而群体运动时能够适应环境的改变，通过交流蜜源信息来寻求最优蜜源。人工蜂群算法的搜索模型包括蜜源、雇佣蜂、观察蜂和侦察蜂，不同的蜜蜂以不同的方式寻找蜜源，在采蜜过程中进行交流交换信息，最后得到最优蜜源。

算法的具体步骤如下：

(1)初始化蜂群

将蜜源抽象为n维搜索空间内的点，且参与寻找蜜源的蜜蜂个数为SN。则在搜索范围内随机初始化的第i个蜜源为

Xi={xi,1,xi,2,…,xi,n}

(14)

xi,j=xmin,j+rand(0,1)(xmax,j-xmin,j)

(15)

其中i=1,2,…,SN；j=1,2,…,n；Xmin,j和Xmax,j分别为搜索范围的最小值和最大值。

通过式(14)和式(15)在搜索空间内随机生成SN个蜜源，分别对应SN个雇佣蜂的初始搜寻位置，且其判定值fi可以根据判定方程得出。

(2)雇佣蜂运动

每个雇佣蜂在执行一次采蜜任务后寻找新的蜜源，单个蜜蜂会与随机选择的附近的蜜蜂交换蜜源信息，通过信息的交换得到新的蜜源位置。蜜源更新方程为

vi,j=xi,j+φi,j(xi,j-xk,j)

(16)

其中k∈{1,2,…,SN}，j∈{1,2,…,n}，且k与j随机从范围内选取。φi,j从[-1,1] 中随机选取。

得到新的蜜源Vi后，每个蜜蜂会与自己之前的蜜源Xi进行比较。根据判定方程的判定值fi，通过贪婪法则进行比较。如果新的蜜源Vi优于Xi，则Vi取代Xi成为新的蜜源，如果Vi并没有优于Xi，则该蜜蜂的蜜源保持为Xi。

(3)选择概率

所有的雇佣蜂在完成搜索蜜源后，在舞蹈区域与观察蜂交换蜜源信息。每只观察蜂的蜜源信息通过所有的雇佣蜂获得，且蜜源的位置会根据花蜜的数量得到选择概率。这个概率的选择是由每个蜜源的适应度决定，概率为

(17)

(18)

每个蜜源的适应度fiti由判定方程的判定值得出，适应度越高的蜜源位置越好。

(4)观察蜂运动

根据选择概率，每只观察蜂从所有雇佣蜂处获得蜜源位置信息。在选择蜜源位置Xi后，依据式(16)更新自己的蜜源位置。运动到新的蜜源位置后，通过贪婪法则进行选择，如果新位置优于雇佣蜂的蜜源位置，则替代雇佣蜂进入蜂群。

(5)侦察蜂运动

侦察蜂的任务在于侦察蜜源位置的更新情况。某个雇佣蜂的蜜源位置被更换的次数超过限定值，则该雇佣蜂需要被淘汰。侦察蜂会根据式(15)在搜索范围内随机产生一个位置，替代该雇佣蜂进入蜂群寻找蜜源。

2.2 引导人工蜂群算法

基本的算法中雇佣蜂和观察蜂都采用式(16)来更新蜜源，即将自己蜜源信息中的一部分与邻近蜜蜂的蜜源信息进行随机交换。这样交换信息更新的方式随机性大，不易陷入局部最优位置。然而，邻近的蜜蜂是随机选取，其蜜源优劣程度未知，则在一定程度上会引导该蜜蜂转向相对差的蜜源处。

引导人工蜂群算法(GABC)在更新蜜源位置时与基本人工蜂群算法不同，该算法选出全局最优的蜜蜂及其蜜源位置，且随着蜂群的运动不断更新全局最优。全局最优的蜜蜂找到了此时蜂群的最佳蜜源，则有责任引导和带领其余蜜蜂向好的蜜源移动。在更新蜜源时采用

vi,j=xi,j+φi,j(xi,j-xk,j)+φi,j(xGbest,j-xk,j)

(19)

式中xGbest,j——全局最优蜜源位置

在引导人工蜂群算法中，雇佣蜂与观察蜂均采用式(19)的方式更新蜜源位置。这样的更新方式，一部分的信息与邻近的蜜蜂进行交换更新，一部分的信息与全局最优蜜蜂交换更新，即可以保证搜索的全局性，不会被局部最优的蜜源干扰，又可以在全局最优蜜蜂的引导下，向更好的蜜源处移动。

3 算例

根据如图1所示的3-RPS机构，以坐标系中心为原点，转动副所在平台半径为ra=274 mm，球副所在平台半径为rb=158 mm。该运动平台的工作空间如表1所示，绕X轴的转动为α，绕Y轴的转动为β。

表1 运动平台工作空间
Tab.1 Workspace of moving platform

参数XYZ位移/mm00[400,700]转角/(°)[-20,20][-20,20]0

以求解α=9°,β=13°,ze=622 mm为例分别采用连续蚁群算法、人工蜂群算法和引导人工蜂群算法进行正解运算。3-RPS并联运动平台的正解数值解运算为已知驱动连杆长度d1=598.849 5 mm，d2=671.584 7 mm，d3=629.495 5 mm，求解得到运动平台的位置和姿态。本文中采用Matlab R2012b进行仿真，运行电脑配置为Intel® Core i7-4510U CPU @ 2.00 GHz 2.60 GHz RAM 7.71 GB。

采用3种算法均为群智能最优化算法，采用仿生方式在种群的基础上进行寻优。3种算法种群数量设置为10，迭代次数为600次，独立运行30次后得到结果进行比较。

从表2中可以看出，人工蜂群算法和引导人工蜂群算法得到的计算值相差不大，误差都小于10-10，比较而言连续蚁群算法计算值的误差较大。图2为3种算法判定值误差曲线。从图2可以看出，连续蚁群算法曲线平缓，收敛速度慢。人工蜂群算法和引导人工蜂群算法分别在迭代170次左右和迭代90次左右收敛，达到最小值，并且引导人工蜂群算法的收敛速度最快。

表3为独立运行30次后，判定方程误差的平均值，标准差以及运行平均时间的比较。从表3可以看出，人工蜂群算法及引导人工蜂群算法的单次运行时间比蚁群算法长，相比较而言，引导人工蜂群算法的单次运行时间比人工蜂群算法短。但是，蚁群算法得到的误差最大，且与人工蜂群算法和引导人工蜂群算法的误差相差非常大，后2种算法得到的误差非常小，优势明显。

表2 各个算法实际值与计算值结果
Tab.2 Results of actual value and calculated value for each algorithm

算法α/(°)β/(°)ze/mm目标值计算值绝对误差目标值计算值绝对误差目标值计算值绝对误差ACO98.859831.40165×10-11313.00181.84503×10-3622621.9995.38574×10-4ABC99.000004.40234×10-111313.00007.75024×10-12622622.0005.12727×10-10GABC99.000001.07034×10-101313.00006.02700×10-10622622.0007.27595×10-12

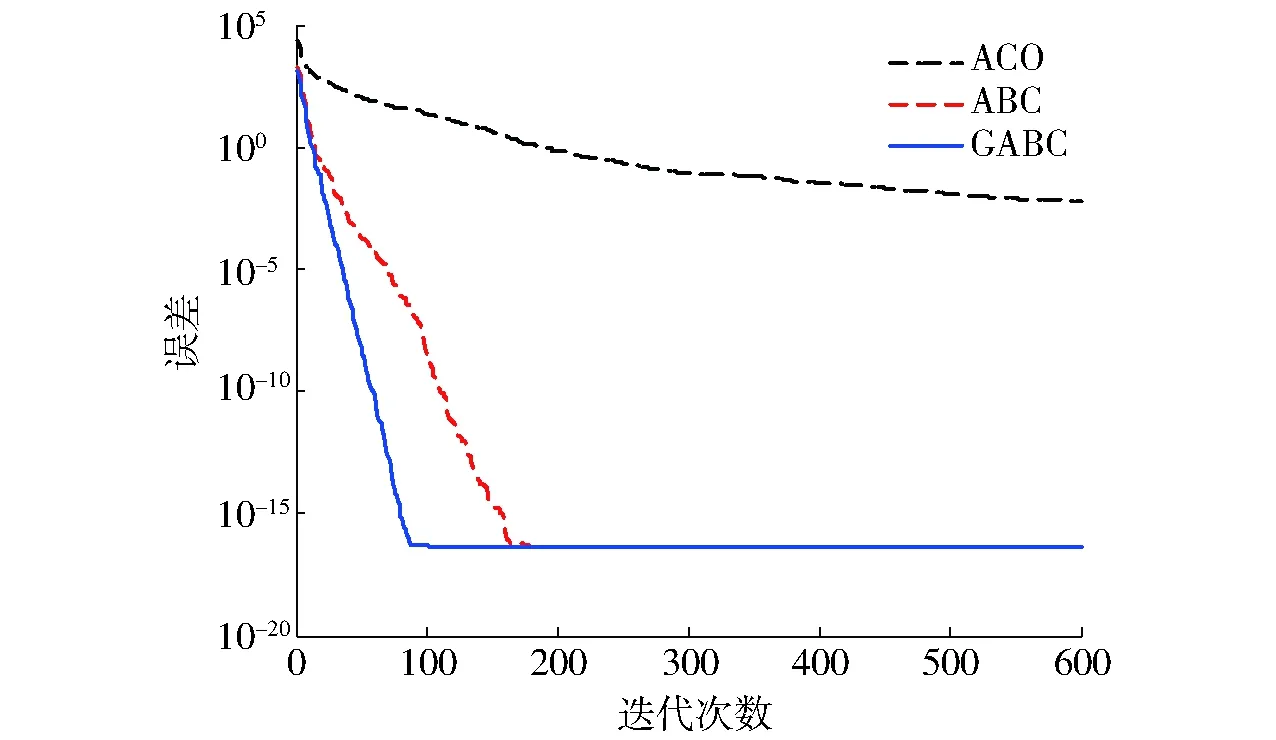
图2 各个算法的误差曲线Fig.2 Fitness error curves of each algorithm

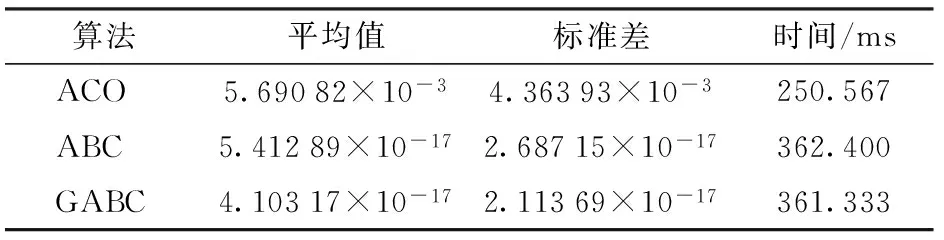
算法平均值标准差时间/msACO5.69082×10-34.36393×10-3250.567ABC5.41289×10-172.68715×10-17362.400GABC4.10317×10-172.11369×10-17361.333

根据工程需要，在实际的运动控制中，3-RPS并联机构运动平台绝对误差达到10-4即可满足需求。人工蜂群算法和引导人工蜂群算法都达到要求，且精度很高。实际控制要求中，精度满足要求是最基本的条件，在运动过程中需要实时计算出机构正解，以达到运动平台的连续运动，因此运行时间直接影响到控制的实时性，此工程的实时控制时间要求为100 ms以下。由此，在3种算法计算精度满足工程实际要求情况下，对运算时间进行比较，在最高迭代次数为600次的基础下，设置判定方程的运算精度为10-5，得到最后的计算值的绝对误差精度在10-4以上，具体的计算值、绝对误差、判定误差以及单次运算时间如表4和表5所示。从这2个表中可以看出，连续蚁群算法在迭代次数内无法达到工程应用要求，且运算时间也大大超出了工程应用实时控制运算时间要求。人工蜂群算法和引导人工蜂群算法的计算值和绝对误差都满足工程应用要求，且运算时间也在实时控制要求以内。引导人工蜂群的收敛速度快，运算的时间最短，非常符合工程应用要求。

表4 各个算法满足精度的实际值与计算值结果
Tab.4 Results of actual value and calculated value met precision requirement for each algorithm

算法α/(°)β/(°)ze/mm目标值计算值绝对误差目标值计算值绝对误差目标值计算值绝对误差ACO98.859831.40165×10-11313.00181.84503×10-3622621.9995.38575×10-4ABC99.000333.39943×10-41312.99945.18093×10-4622622.0001.60948×10-4GABC99.000121.26283×10-41313.00003.14427×10-5622622.0002.23827×10-4

表5 各个算法满足精度的判定误差比较
Tab.5 Comparison of fitness error met precision requirement for each algorithm

算法平均值标准差时间/msACO5.69082×10-34.36393×10-3250.567ABC5.72884×10-53.02445×10-569.800GABC5.73793×10-53.35311×10-538.300

具体判定方程的误差值收敛情况如图3所示，此误差达到了10-4以下，且收敛速度非常快，引导人工蜂群优势明显。

图3 各个算法满足精度要求误差曲线Fig.3 Fitness error curves met precision requirement of each algorithm

该3-RPS并联机构运动平台在试验过程中需到达工作空间内任意位置，要求控制连续运动，实时得到机构的运动学正解。如表6所示，列出了5种不同情况的位姿，采用引导人工蜂群算法进行求解，求解精度和求解时间均满足工程应用运动控制要求。

表6 不同情况下引导人工蜂群计算结果
Tab.6 Results of calculated value of GABC in different situations

序号参数真实值计算值绝对误差适应误差时间/msα/(°)99.000121.26283×10-41β/(°)1313.00003.14427×10-55.73793×10-538.3000ze/mm622622.0002.23826×10-4α/(°)-17-16.99972.55598×10-42β/(°)88.000171.68791×10-45.83262×10-537.9000ze/mm436436.0002.77078×10-4α/(°)44.000141.40896×10-43β/(°)7-7.000131.31228×10-44.95234×10-533.8333ze/mm509509.0001.64332×10-4α/(°)-13-13.00001.37617×10-44β/(°)-19-18.99992.95497×10-44.76015×10-536.7667ze/mm574573.9999.32082×10-5α/(°)1818.00033.41270×10-45β/(°)1110.99963.08625×10-45.97693×10-534.6000ze/mm695694.9992.65672×10-5

4 结束语

对3-RPS并联机构运动平台进行运动学分析，建立了带约束条件下运动学正解非线性方程组，将多目标非线性方程转换为单目标判定方程优化。采用人工蜂群算法，通过全局最优进行引导的方式，得到高精度低运算时间的并联运动平台位姿参数，达到工作空间内控制策略的连续求解要求。实际仿真算例验证了该算法在并联机构运动学正解上的有效性和优势。

1 孔宪文, 黄真. 3-RPS 控制位置用并联机器人机构的反解[J]. 机械科学与技术, 1999, 18(3): 424-426. KONG Xianwen, HUANG Zhen. Inverse displacement analysis of 3-RPS regional parallel manipulators[J]. Mechanical Science and Technology, 1999, 18(3): 424-426. (in Chinese)

2 鲁开讲, 牛禄峰, 刘亚茹, 等. 3-RPS 并联机构奇异位形及工作空间研究[J]. 农业机械学报, 2007, 38(5): 143-146. LU Kaijiang, NIU Lufeng, LIU Yaru, et al. Research on singular configuration and workspace of 3-RPS parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(5): 143-146. (in Chinese)

3 陈修龙, 孙先洋, 邓昱. 4-UPS-RPS 空间5自由度并联机构运动学分析 [J/OL]. 农业机械学报, 2013, 44(8): 257-261. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130844&flag=1. DOI：10.6041/j.issn.1000-1298.2013.08.044. CHEN Xiulong, SUN Xianyang, DENG Yu. Kinematics analysis of 4-UPS-RPS spatial 5-DOF parallel mechanism[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(8): 257-261. (in Chinese)

4 GALLARDO J, OROZEO H, RICO J M. Kinematics of 3-RPS parallel manipulators by means of screw theory[J]. The International Journal of Advanced Manufacturing Technology, 2008, 36(5-6): 598-605.

5 RAO P S, RAO N M. Position analysis of spatial 3-RPS parallel manipulator[J]. International Journal of Mechanical Engineering and Robotics Research, 2013, 2(2): 80-90.

6 任文博, 颜兵兵, 殷宝麟, 等. 3-RPS 型并联机构运动正解的研究[J]. 佳木斯大学学报: 自然科学版, 2014, 32(3): 412-414. REN Wenbo, YAN Bingbing, YIN Baolin, et al. Research on direct kinematics for 3-RPS parallel mechanism[J]. Journal of Jiamusi University Natural Science Edition, 2014, 32(3): 412-414. (in Chinese)

7 牛禄峰. 利用特征列方法求解并联机构位置正解[J]. 机械设计, 2007, 24(8): 28-30. NIU Lufeng. Using the characteristic row method to solve the positional normal solution of parallel mechanism [J]. Journal of Machine Design, 2007, 24(8): 28-30. (in Chinese)

8 YANG C F, ZHENG S T, JIN J, et al.Forward kinematics analysis of a 3-PRS parallel manipulator[J]. World Academy of Science, Engineering and Technology, 2010, 17: 1264-1270.

9 谢志江, 梁欢, 宋代平. 基于连续蚁群算法的 3-RPS 并联机构正解[J]. 中国机械工程, 2015, 26(6): 799-803. XIE Zhijiang, LIANG Huan, SONG Daiping. Forward kinematics of 3-RPS parallel mechanism based on a continuous ant colony algorithm[J]. China Mechanical Engineering, 2015, 26(6): 799-803. (in Chinese)

10 李树军, 王阴, 王晓光. 3-RPS 并联机器人机构位置正解的杆长逼近法[J]. 东北大学学报: 自然科学版, 2001, 22(3): 205-207. LI Shujun, WANG Yin, WANG Xiaoguang. Forward position analysis of 3-RPS in-parallel manipulator using self-modified successive approximation method[J]. Journal of Northeastern University: Natural Science, 2001, 22(3): 205-207. (in Chinese)

11 韩方元, 赵丁选, 李天宇. 3-RPS 并联机构正解快速数值算法[J]. 农业机械学报, 2011, 42(4): 229-233. HAN Fangyuan, ZHAO Dingxuan, LI Tianyu. A fast forward algorithm for 3-RPS parallel mechanism [J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(4): 229-233. (in Chinese)

12 陈长忆, 车林仙. 应用粒子群算法的 3-RPS 并联机器人机构位置正解[J]. 现代制造工程, 2006(5): 77-79. CHEN Changyi, CHE Linxian. Forward position analysis of 3-RPS in-parallel manipulators based on particle swarm optimization[J]. Modern Manufacturing Engineering, 2006(5): 77-79. (in Chinese)

13 ZHANG Hongli, REN Tiantian, PAZILAI Mahemuti. Forward position solution of 3-RPS in-parallel manipulator based on particle swarm optimization[C]∥The 26th Chinese Control and Decision Conference (2014 CCDC), IEEE, 2014: 4171-4177.

14 杜义浩, 谢平, 田培涛, 等. 基于改进粒子群算法的并联机器人运动学精度提高新方法[J]. 中国机械工程, 2012, 23(16): 1938-1942. DU Yihao, XIE Ping, TIAN Peitao, et al. A new method for improving kinematics accuracy of parallel robot based on improved PSO[J]. China Mechanical Engineering, 2012, 23(16): 1938-1942. (in Chinese)

15 房立金, 党鹏飞. 基于量子粒子群优化算法的机器人运动学标定方法[J]. 机械工程学报, 2016, 52(7): 23-30. FANG Lijin, DANG Pengfei. Kinematic calibration method of robots based on quantum-behaved particle swarm optimization[J]. Journal of Mechanical Engineering, 2016, 52(7): 23-30. (in Chinese)

16 RAO N M, RAO K M. Dimensional synthesis of a spatial 3-RPS parallel manipulator for a prescribed range of motion of spherical joints[J]. Mechanism and Machine Theory, 2009, 44(2): 477-486.

17 吴小勇, 谢志江, 宋代平, 等. 基于改进蚁群算法的 3-PPR 并联机构位置正解研究[J/OL]. 农业机械学报, 2015, 46(7): 339-344. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150748&flag=1. DOI：10.6041/j.issn.1000-1298.2015.07.048. WU Xiaoyong, XIE Zhijiang, SONG Daiping, et al. Forward kinematics of 3-PPR parallel mechanism based on the improved ant colony algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 339-344. (in Chinese)

18 GAO W, LIU S. A modified artificial bee colony algorithm[J]. Computers & Operations Research, 2012, 39(3): 687-697.

19 JADHAV H T, ROY R. Gbest guided artificial bee colony algorithm for environmental/economic dispatch considering wind power[J]. Expert Systems with Applications, 2013, 40(16): 6385-6399.

20 ZHU G, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173.

21 王慧颖, 刘建军, 王全洲. 改进的人工蜂群算法在函数优化问题中的应用[J]. 计算机工程与应用, 2012, 48(19): 36-39. WANG Huiying, LIU Jianjun, WANG Quanzhou. Modified artificial bee colony algorithm for numerical function optimization[J]. Computer Engineering and Applications, 2012, 48(19)：36-39. (in Chinese)

22 毕晓君, 王艳娇. 改进人工蜂群算法[J]. 哈尔滨工程大学学报, 2012, 33(1): 117-123. BI Xiaojun, WANG Yanjiao. A modified artificial bee colony algorithm and its application[J]. Journal of Harbin Engineering University, 2012, 33(1): 117-123. (in Chinese)

23 任子武, 王振华, 孙立宁. 基于改进人工蜂群算法的并联机器人正运动学解[J]. 机械工程学报, 2013, 49(13): 48-55. REN Ziwu, WANG Zhenhua, SUN Lining. Forward kinematics solution for parallel manipulators based on improved artificial bee colony algorithm[J]. Journal of Mechanical Engineering, 2013, 49(13): 48-55. (in Chinese)

24 毕晓君, 王艳娇. 加速收敛的人工蜂群算法[J]. 系统工程与电子技术, 2011, 33(12): 2755-2761. BI Xiaojun, WANG Yanjiao. Artificial bee colony algorithm with fast convergence[J]. Systems Engineering and Electronics, 2011, 33(12): 2755-2761. (in Chinese)

25 秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2): 377-385. QIN Quande, CHENG Shi, LI Li, et al. Artificial bee colony algorithm: a survey[J]. CAAI Transactions on Intelligent Systems, 2014, 9(2): 377-385. (in Chinese)

Forward Kinematics Optimization of 3-RPS Parallel Manipulator Based on Global-best Artificial Bee Colony Algorithm

MAO Bingyan XIE Zhijiang WU Xiaoyong YUAN Yuejun

(StateKeyLaboratoryofMechanicalTransmission,ChongqingUniversity,Chongqing400044,China)

A fast numerical algorithm for the forward kinematics optimization of 3-RPS parallel manipulator was presented. Through numerical optimization methods, the problem of forward kinematics of parallel robot was inverted to minimization problem. According to the optimization of forward kinematics for 3-RPS parallel manipulator, the forward kinematic functions, which were the multi-objective nonlinear equations with constraint, were built based on numerical method. The fitness function was established to achieve the optimization of single objective, and the minimum optimization was solved based on the global-best artificial bee colony algorithm. The information carried by employed bees was exchanged among the neighboring bees. The position information was exchanged randomly and the neighborhood bees were chosen randomly as the standard artificial bee colony algorithm. In addition, for the global-best artificial bee colony algorithm, the global best bee which carried the best position information would guide all bees to move to the better position, and convergence fast to the best position. As the simulation result of 3-RPS forward numerical kinematics showed, compared with continuous ant colony algorithm and standard artificial bee colony algorithm, the global-best artificial bee colony algorithm was an effective way, which with high precision and high speed, to solve forward kinematics of parallel manipulators.

parallel manipulator; artificial bee colony algorithm; forward kinematics

10.6041/j.issn.1000-1298.2017.01.045

2016-05-27

2016-07-25

国家自然科学基金项目(U1530138)

毛冰滟(1991—)，女，博士生，主要从事机器人技术和优化算法研究，E-mail: sucaogen@163.com

谢志江(1962—)，男，教授，博士生导师，主要从事机械创新设计、机电一体化及设备故障诊断研究，E-mail: xie@cqu.edu.cn

TH112

A

1000-1298(2017)01-0339-07