5次对称群S5的一类子群的一个构造方法
唐耀平 吴建平 周立平
5次对称群S5的一类子群的一个构造方法
唐耀平吴建平周立平
(湖南科技学院 理学院,湖南 永州 425199)
由于有限群的Lagrange定理的逆定理不成立。因此,要确定S5的各阶子群是较困难的。文章通过次对称群的基本概念及5-循环置换各次方幂的计算及研究,找到了S5的一类子群的构成规律,并使用构造性方法给出了3、5、6、8阶子群。
5次对称群;子群;Lagrange定理;循环置换
1 引 言
关于子群及个数的研究在计算机通信、代数编码及计数理论研究中都具有重要意义。次对称群S是一个重要的群,由定理知,任何有限群都同构于对称群S的一个子群. 所以,只要能够解决S的所有子群及这些子群的结构,则任意有限群的问题就得到完全解决。但较大时,要找出S的全部子群及决定各子群的结构仍然困难。文献[2]讨论了4的所有子群及其结构,文献[3-5]讨论了6的所有子群及两类子群的构造方法,文献[6]讨论了5的2、4、20、24阶的子群,文献[7-13]给出了5的子群5的一些性质及其结构。这些文献表明对次对称群S及其子群的讨论依然是非常活跃的。本文使用有限群的定理及次对称群的结果,构造性地给出了5的3、5、6、8阶子群,文中所引用的符号见文献[1]。
2 预备定理
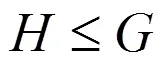


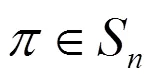
3 主要结果
3.1 5-循环置换幂的计算
‖ ‖ ‖ ‖ ‖
(5)5-循环置换24个,由上述5-循环置换幂的计算,全部24个5-循环置换按其1,2,3,4次方幂进行分组,共为6组,分别为:

,,, ,,,

,, ,,
(7)3×2-循环置换的乘积20个,按3-循环置换与不相交的2-循环置换的乘积进行,即
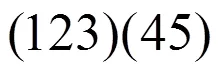
,,,

,,,
3.2 构造S5的子群
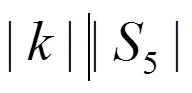
命题15有10个3阶子群.
证明:由定理1及推论,由于3是素数,因此3阶群必为循环群,且由一个3阶元生成,又由定理3,3阶元的平方是其逆元,因此5有10个3阶子群,即:
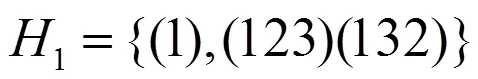
,,,

.
命题25有6个5阶子群.
证明:由定理1及推论,5的5阶子群的元素的阶只可能为1、5,又由于5是素数,因此5阶群必为循环群,所以组成5的5阶子群的元素除单位元外,只可能由5-循环置换的元素组成,即:

,
命题35有30个6阶子群.
证明:由定理1及推论,5的6阶子群的元素的阶只可能为1、2、3、6,所以组成5的6阶子群的元素除单位元外,只可能由2-循环置换、3-循环置换、2×2-循环置换的乘积、3×2-循环置换的乘积、6-循环置换或它们的元素组合形式,即;
(1)经计算由单位元、2-循环置换、3-循环置换与3×2-循环置换的乘积形式的元素组成5的10个子集均为5的6阶子群,即:

,,

,,
每个子群的构浩方法(本文取、、、、为5-循环置换的5个元素):
(1.l)从命题2中任意选定一个3阶子群,取其3阶元(如()).
(1.2)取与这个3阶元不相交的2阶元(如()).
(1.3)将2阶元与3阶子群相乘即得.
(2)经计算由单位元、3-循环置换与3×2-循环皆换的乘积形式的元素组成5的10个子集均为5的6阶子群,即:
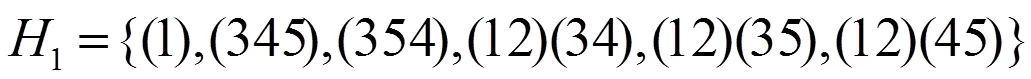
,,

,,
每个子群的构造方法:
(2.1)从命题2中任意选定一个3阶子群,取其3阶元(如()).
(2.2)取这个3阶元3个数字的任意二者组合,组成2阶元(如()、()、()).
(2.3)取与这个3阶元不相交的2阶元(如()).
(2.4)将()与第2步中任一个2阶元(如())相乘得2×2-循环置换的乘积(如()()).
(2.5)将这个2×2-循环置换乘积形式的元与第1步中3阶子群相乘即得.
(3)经计算由单位元、2-循环置换与3-循环置换的元素组成5的10个子集均为5的6阶子群,即:

,,

,,
每个子群的构造方法:
(3.1)从命题2中任意选定一个3阶子群,取其3阶元(如(abc)).
(3.2)取这个3阶元3个数字的任意二者组合,组成2阶元(如(ab)、(ac)、(b c)).
(3.3)取第2步中任一个2阶元(如(ab)).
(3.4)将这个2-循环置换的元与第1步中3阶子群相乘即得.
命题45有15个8阶子群.
证明:由定理1及推论,5的8阶子群的元素的阶只可能为1、2、4、8,所以组成5的6阶子群的元素除单位元外,只可能由2-循环置换、4-循环置换、2×2-循环置换的乘积或它们的元素组合形式,即:
经计算由单位元、2-循环置换、4-循环置换与2×2-循环置换的乘积形式的元素组成5的15个子集均为5的8阶子群,即:
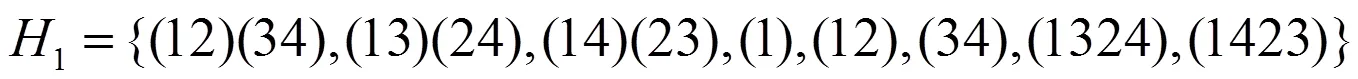
,
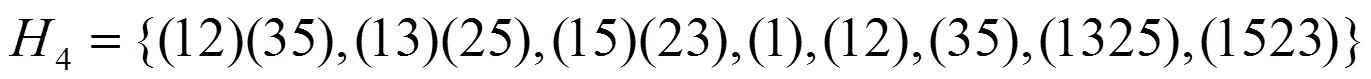
,

,

,
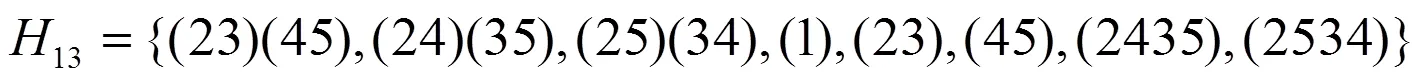
,
每个子群的构造方法:
(1)每个子群的前三个元素是从文章所给的5组2×2-循环置换的乘积中任取的一组,再加上单位元.
(2)第五、六个元素为前三个的第一个2×2-循环皆换的拆分.
(3)第七、八个元素分别为第二、三个2×2-循环置换按顺序合并成4-循环置换.
(4)在所取的2×2-循环置换的3个元素中按轮回排列先后顺序.
[1]徐明耀.有限群导引[M].北京:科学出版社,1999.
[2]孙自行,崔方达.4次对称群的子群个数及其证明[J].阜阳师范学院学报,2005,(4):13-16.
[3]黄本文.对称群6的一类子群[J].武汉交通科技大学学报,2000,(2):129-134.
[4]Huang Ben-wen.The subgroups of symmetric groups6[J].Applied Mathematics A Journal of Chinese Universities,2001,(1):31-35.
[5]Huang Ben-wen.The subgroups of symmetric group6[J].Journal of Wuhan Transportation University,2000,(2):129-134.
[6]班桂宁,吴建平,张中建,张玉.5的一类子群的一个构造方法[J].吉首大学学报(自然科学版),2008,(4):1-4.
[7]Machi A,Siconofi A.A new characterization of5[J].Arch.Math.1977:385-388.
[8]Arad Z,Chillang D,Herjog M.Classification of finite groups by a maximal subgroup[J].Journal of Algebra,1981,(1):235-244.
[9]Shi Wu-jie.Characterization of A5and the finite groups in which every element has prime order[J].Journal of Southwest Teachers University,1984,(1):36-40.
[10]Shi Wu-jie.Characterization proerty of5[J].Journal of Southwest Teachers University,1986,(3):11-14.
[11]Huang Ben-wen.The characterization of5[J].Wuhan University Journal of Natural Sciences,1997,(4):405-410.
[12]孙自行.5次交错群5的10阶子群的一个构造方法[J].电子科技大学学报,2006,(3):419-422.
[13]包霞,焦艳.5的一类12阶子群的构造[J].西北民族大学学报,2007,(3):11-15.
(责任编校:何俊华)
2017-05-09
湖南省自然科学基金项目(项目编号12JJ3077)。湖南省教育厅资助科研项目(项目编号12C0688)。
唐耀平(1973-),男,湖南永州人,教授,硕士,主要从事数值代数及群体决策研究。
O152
A
1673-2219(2017)10-0001-04

