基于学生差异发展专业服务的高等数学教学改革研究
(山东农业工程学院,山东 济南 250100)
前言:作为基础学科的高等数学课程,要适应新形势下的人才培养目标,从专业需求出发,建设新的课程体系,高等数学课程的开设,不仅要为专业知识的掌握打好基础,更要为学生的可持续发展奠定基础,为今后长期的学习做好入门准备,在明确培养目标的前提下,充分考虑学生差异发展的个体需求,达到学生差异发展下数学知识应用与综合素质提高有机结合的目的。
一、高等数学教学的现状
不可否认,在国家的进步和发展中,教育在其中的推动力量是无可非议的,而教育的核心则是将所学与所用有机的结合,反思过去的高等数学的教学,主要存在以下的问题:
(一)数学与专业案例有机融合较少。
对于学生来说,学生只是掌握了课本上的数学知识,却未能将数学与自己的专业相结合,完全忽视了高数对解决自己专业问题的重要性。对于老师来说,在数学领域有着很高的教学水平,但对所教专业用到的数学知识了解不够,没有真正做到学生差异化发展需求因材施教,缺乏与专业教师的沟通,因而专业应用案例较少。
(二)高等数学的教学内容理论性较强。
随着各专业人才培养方案、教学计划的调整,产生了教学内容与教学课时的矛盾,内容相对较多、理论性较强,同时专业需求对教学内容也有更高的要求。
(三)过多的考虑该课程知识体系的系统性和完整性。
虽然各专业对高等数学课程的知识需求是不完全相同的,在课程体系上过多考虑这一学科的完整性、计算上的精确、逻辑上的严谨,在教学内容上面面俱到,存在过难过深的内容,内容处理不够得当,由此专业特色和需求基本上不能兼顾,专业特色的发展受到了限制。
二、基于学生差异发展专业服务的高等数学教学改革
(一)明确课程改革目标,更新课程建设理念。
课程改革必须先从理念开始,以应用能力和职业素养为主线,打破过去追求知识体系的完整性和系统性,重构课程标准和教学内容,改革教学方法和教学模式,提高教学效果。
(二)构建课程标准,精选教学内容。
1、构建突出应用能力培养的课程标准。
本着以应用为目的,以服从人才培养方案及专业的培养目标为依据,将课改与专业建设相结合,教学内容和专业发展相联系。考虑差异化发展需求的教学对象调整教材内容,根据不同专业的特点和后续课程的要求,明确每一章节需要掌握、了解、选学的教学内容。本文制定数学课程改革建设目标如下:
(1)课程总体目标。
提高学生的数学素养,学习高等数学的基本知识与技能,培养学生数学思考能力,初步掌握运用数学知识解决实际问题的数学建模能力。
(2)课程知识目标。
掌握高等数学的基本知识;掌握实际工作中遇到的必要的导数、微分、积分等的计算方法以及计算途径;熟悉现代数学技术,如Matlab,Lingo的使用方法;拥有运用数学知识解决实际问题的能力。
(3)课程应用目标。
运用高等数学理论,建立简单优化模型,掌握高等数学在经济、工程实际问题中的应用.如空间解析几何的基本知识,在工程制图课程的应用,常微分方程在工程、经济问题中的应用;用数学建模方法解决简单的应用问题。
2、由学科型课程体系转变为满足差异化发展专业服务需求的项目化课程体系。
课程体系由两个层次构成,第一层次为:“基础核心项目”,主要内容是一元函数微积分,它是培养学生所必须具备的数学基本文化和核心能力而设置的,是每个学生都必须学习的数学内容;第二层次是“差异化发展需求项目”,主要是基于差异化发展、专业服务构建的。
3、转变教学理念,融入数学建模思想。
高等数学教师应到相应的二级学院相关专业进行调研,了解该专业的人才培养方案及高等数学知识的需求等内容,把数学建模的思想融入高等数学教学中。
4、结合专业需求,整合课程内容。
通过对近40个专业方向的调研,对学科所需高等数学知识进行粗化分类,分别对理工类专业,财经、管理类专业所需数学知识点进行调查,分析,归类,然后把教学内容按模块分为基础模块,专业需求模块和深造与拓展模块。学科模块划分如表1所示:

表1 数学课程教学内容模块划分
基础模块是各专业必须要求的数学基础知识,专业组合模块是为满足学生差异化发展需要,使之更有针对性和实用性,深造与拓展模块是为学生专升本、考研数学竞赛及数学建模竞赛的需要。
5、课上课下、线上线下相结合分层次教学,以适应不同学生的发展需求。
在同一课堂授课模式下,灵活运用教材,以适应学生的不同需求。真正实现因材施教,因才施教,针对学生的差异化发展需求,课程教学实行精讲加课外辅导形式,形成课堂内外分层次教学,在课堂教学中我们实施大圈套小环的分层次教学法,使每一层次的学生根据学生的特点,即学习能力、理解能力等的不同进行教学,对于基础比较薄弱的,就注重基本知识的讲解,巩固基本知识,等达到一定理解层次时,再逐层深入达到跳一跳,够得着的希望。具体做法是把内容,例题,习题分为必备层次,专业层次,知识延拓层次。充分调动学生学习的主动性和积极性,形成一系列开放的、动态的、师生互动的教学方法。借助于多媒体辅助教学,共享山东大学的《高等数学-微积分》慕课,与我院教学相结合,设计混合学习方法,指导学生课下进行视频内容的学习、练习操作与交流心得,课堂上进行内容的重点分析、知识总结,解决学生存在的问题,既增强师生交流与个性化沟通,又提高了学生的学习兴趣与成效,既注重面向全体学生,又注重学生差异发展,学生受益匪浅,达到教学过程及效果的最优化。
6、开设数学建模选修课,把数学建模教学与基本知识教学有机结合。
高等数学课程要为学生的可持续发展奠定基础,需要把工具数学,实用数学有机结合.课程设置方面我们在学校的支持下开设了数学建模选修课,全校各专业学生踊跃参加,2015、2016年连续两年每年均有280多人参加数学建模选修课,课堂外我们成立了数学建模协会,鼓励学生从实践中发现问题,解决问题,积极组织学生参加数学建模大赛,使数学课程应用“活起来”.2016年我校组织14个队参加“全国大学生数学建模大赛”,其中两个队获省级一等奖,三个队获省级二等奖,一个队获省级三等奖。如图1所示:

图1 获奖情况
7、实行多元化考核,实现不同专业不同模式的考核方式。
针对传统教学模式一刀切的弊端,根据差异性发展需求,不同专业对高等数学的要求,分别制定相应的考核标准,包括各种考核成绩的类型和比重。比如对于经济类的学生,曲面积分和曲线积分的要求就相对低一些,只需要了解即可,而对于工程类的学生,则要求相应提高,需要掌握,而在平时成绩和期末考试中则需要有不同的考核要求和标准。将学生的综合考试成绩分为两大部分。第一是采用笔试(占70%),它主要考查学生对数学基本知识和基本技能的掌握情况;第二是过程性考核(占30%),即对学生学习过程考核情况等。考试改革方案如下:
(1)总评成绩由三部分组成。
平时成绩1占10%;平时成绩2占20%;期末考试成绩3占70%。
(2)各考试成绩涵盖内容。
平时成绩1包含:数学作业、课堂问题讨论、出勤;平时成绩2包含单元测题、网上在线(图1)、数学知识应用等;期末考试成绩3的形式有填空题;选择题;计算题;应用题及证明题。
(3)增加学生数学实验的考核比重,数学实验则包括学生的数学竞赛,数学建模竞赛以及上机学习。
结合我校建设应用型本科院校的定位,数学作为一门重要的基础课程,培养学生的动手能力和应用能力则不容忽视,随着计算机的广泛应用以及数学软件的日益完善,在教学过程中引进了对数学软件的介绍和应用,如通过数学建模,引导学生学习Matlab软件和Lingo软件等,引导学生利用数学软件自己动手去处理诸如微积分、统计学、线性代数中的某些问题,让学生可以轻松地利用计算机完成一些课外作业和计算。
8、采用无纸化考试考核方式,实现无纸化考试分析模式,更好的反应学生的学习效果,同时提高学生的学习兴趣。
试卷分析是评价学生学习效果和教师教学质量的重要依据,是高校考试过程中的一个重要环节,因此做好试卷分析的研究意义重大。采取无纸化考试考核方式,可以对考试学生的各项综合指数有更明确和清晰的认识。包括:分析年级、专业、学生人数、学生试卷、得分数以及学生每题得分数。在此基础上,得出平均成绩、标准差、每分数段人数、最高分、最低分,最后得出分析结果。从而极大地方便了老师对学生的评价和及学生的自我评价。

图2 学生在进行无纸化在线考试
针对学生差异发展,考试考核方式的总评成绩比较及学生对考试计分法的认同性调查结果,针对两种不同的记分方法进行问卷调查所起到的效果如表2。

表2 试卷考试传统记分与改革记分学生认同情况调查表
表2显示,传统记分法与改革记分法学生的认同性有明显不同。考试方法的合理性,考试成绩的可靠性,促进学习的效果,考试信心的增强四项认同人数分别为19.5%、20.0%、48.1%、和24.6%;改革记分法四项的认同性分别为 87.5%、85.4%、94.3%和89.5%,特别是对学生促进学习的效果起到了明显的作用;学习压力增强是反向题,该项显示改革记分法可以减轻学生的学习压力,认可的学生比例占71.6%。实践证明,多元化的知识考评机制,有效的杜绝了考前死记硬背,考后一片空白的短期效应。
基于差异发展专业服务数学课程研究总体框架如图3所示:
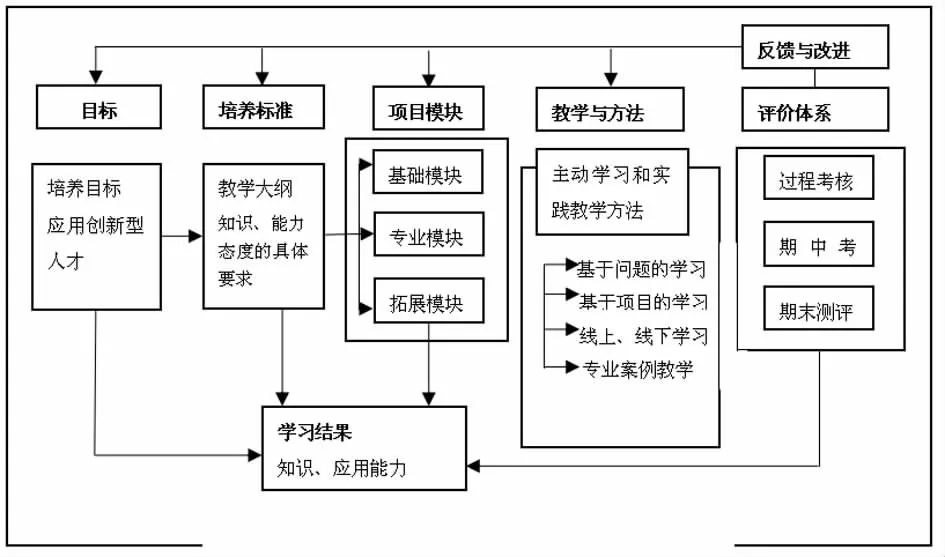
图3 课程研究总体框架
三、结语
总之,在高等数学教学过程中施以差异化发展服务专业的教学理念,提出了以差异化发展专业服务的高等数学教学方式,该方式要求高等数学课程教师,不仅精通高等数学知识,还需要了解不同专业对数学相关知识的要求,将数学课程细分为多个分支,在保证基础知识教学的同时,将有关的数学内容嵌入专业,这样设置的课程表面上内容浅化,实则知识深度却在增加,不仅仅是为了专业学习的应用,更是一种学习和思考以及创新能力的培养。因此解决教学内容厚重与应用的矛盾,适应不同学生的发展需求激发学生的积极性,培养学生学习、创新、创造等各方面的能力。
[1]陶颖华.高职院校高等数学考核制度改革研究[J];2008.07.22.
[2]田芳,海虹.“高等数学”课程与专业相结合教学模式研究---以宁夏师范学院为例[J];2015.06.20.
[3]王德印.基于专业需求的高等数学教学改革研究[J];2010.06.20.
[4]文传军,刘坤,许定亮.目标驱动、专业结合的高等数学课程教学研究—以常州工学院高等数学教学为例.

