课改下如何提高学生的数学解题能力

戴琼

（浙江省诸暨市马剑镇中）

课改下如何提高学生的数学解题能力

戴琼

（浙江省诸暨市马剑镇中）

提高学生的数学解题能力是数学教学中的主要任务之一，也是提高学生考试能力、锻炼学生知识应用能力的基础。所以，为了提升学生的数学素养，锻炼学生的数学解题能力，更为了凸显学生的课堂主体性，锻炼学生的基本学习能力，在数学教学时，教师要改变以往一讲到底的模式，要通过恰当教学活动的组织从多角度、全方位入手来提高学生的数学解题能力，进而为学生考试能力的提高做出相应的贡献。

解题能力；初中数学；基础；分析；数学思想

一直以来，初中数学教学的主要任务就是确保学生掌握基本的数学知识应对考试，至于解题能力的培养仅是依靠题海战术来达到目的。但事实上并没有真正对学生解题能力进行专门性和有针对性的锻炼和提高。所以，为了改变这一现象，在数学教学中，教师要转变教育教学观念，从多角度入手来提高学生的数学解题能力。因此，本文就从以下几个方面入手对如何提高学生的数学解题能力进行论述。

一、抓基础，提高数学解题能力

抓基础是指让学生掌握基本的概念和相关的定理、定律，是学生解题的基础，也是提高解题能力的保障。所以，在新课程改革下，为了提高学生的解题能力，也为了提高学生的数学学习质量，我们首先要做的就是帮助学生真正掌握数学基础知识，真正理解数学思想，了解知识的形成本质，这样才能在灵活运用中确保数学解题能力获得大幅度提高。

例：已知：如图，AB=DC，AD=BC，O是BD中点，过O的直线分别与DA、BC的延长线交于E、F。求证：OE=OF。

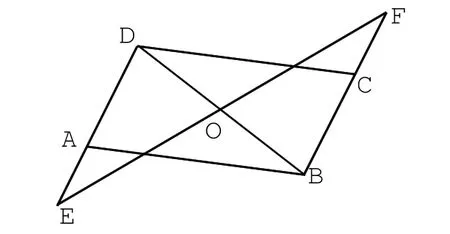
分析该题，我们可以知道，学生要想顺利地解答出这道题，首先要掌握平行四边形的判定定理，即“两组对边分别相等的四边形是平行四边形”。之后，再根据“内错角相等”以及“角边角”的三角形全等的判定定理进行证明。这样就能得出证明结论。具体的解题过程不再详细解答。但是，从分析过程中我们可以看出，该题考查了平行四边形的判定、内错角、全等三角形的判定三个方面的基础知识，如果学生对任何一个知识点没能熟练掌握都不能顺利地将该题解答出来，当然，学生的解题能力也是不会得到提高的。所以，在提高学生解题能力之前，我们必须要确保学生能够掌握数学基础知识，因为这是学生进行解题的依据，也是基础。

二、析题目，培养数学解题能力

所谓的分析题目是指让学生在相关试题的比较中，在多种思路的解题中灵活运用知识，同时也能丰富学生的解题思路，发散学生的数学思维。简单说就是借助一题多解和一题多变来提高学生的数学解题能力，以为学生解题能力的大幅度提高打下坚实的基础。

例如：在四边形ABCD中，AB=CD，点E，F分别是BC，AD的中点，延长BA，CD分别与EF的延长线相交于点H、G，求证：∠BHE=∠EGC。

这是一道一题多解题，所以，为了提高学生的解题能力，在解答时，我鼓励学生从多角度寻找该题的解答思路，这样不仅能够拓展学生的思路，锻炼学生的解题能力，而且对学生知识视野的拓展，对学生的发展都有着密切的联系。因此，在该题的解答时，学生提出了下面几种解题思路，如，思路一：连结AC，并取AC的中点P，连结PE、PF。思路二：过点D，B分别作DM∥AB，BM∥AD，BM、DM相交于点M，连结MC的中点P，连结EP、DP，等等。在这里不再进行画图和详细的解答。但是，从学生多角度的思考和问题解答中，我们可以看出，学生多种方法的解答对学生知识利用能力的锻炼，对高效数学课堂的实现都有着密切的联系。所以，一线教师要鼓励学生自主分析试题，通过丰富解题思路，对比题干来为学生健全的发展奠定坚实的基础。

三、渗思想，锻炼数学解题能力

众所周知，掌握了数学思想，就是掌握了数学的精髓。换句话说就是通过掌握数学思想，了解知识的本质来提高学生的数学解题能力。所以，在数学教学时，教师在教学时要有意识地对基本的数学思想进行渗透，要通过相关练习题的分析来提高学生的数学解题能力，同时也为学生数学素养的全面提升做好保障性工作。

以“数形结合思想”为例，如，已知y=ax2+bx+c中a<0，b>0，c< 0，Δ<0，函数的图象过_______象限。这是一道基本的函数试题，但要是要单凭知识的分析和想象力进行解答是非常容易出错的，也是不利于学生解题能力的提高的。所以，在解题时，我们要有意识地渗透数形结合思想，这样更加直观，也方便学生进行解答，这对学生解题能力的提高以及解题思路的形成都有着密切的联系。

总之，在素质教育思想的影响下，教师要从全方位、多角度入手来提高学生的解题能力，使学生在主动解答、自主应用知识中掌握基本的数学知识，同时也为学生考试能力以及综合数学素养的形成做出相应的贡献。

［1］楼黄芳.论怎样提高初中学生的数学解题能力［J］.时代教育，2013（6）.

［2］周粉美.初中数学教学中提高学生解题能力的技巧［J］.考试周刊，2013（75）.

·编辑 温雪莲