具有饱和输入和通信约束的多智能体系统的包含控制

方建印,谢欣欣，2

( 1.河南工程学院 理学院,河南 郑州 451191; 2.郑州大学 数学与统计学院,河南 郑州 450001)



具有饱和输入和通信约束的多智能体系统的包含控制

方建印1,谢欣欣1，2

( 1.河南工程学院 理学院,河南 郑州 451191; 2.郑州大学 数学与统计学院,河南 郑州 450001)

研究了有向拓扑下具有饱和输入和通信约束的线性多智能体系统的包含控制问题,利用代数图论和Lyapunov控制方法证明了相应结论.假设系统是有界输入渐近零可控的且任意追随者至少存在一个领导者到它有一条有向道路,若持续通信时长大于某一阈值,利用代数Riccati方程设计的低增益间歇反馈控制协议可以使系统达到半全局包含控制.最后,给出仿真实例证明了理论分析的正确性.

线性多智能体系统; 有向拓扑; 输入饱和; 间歇通信; 半全局包含控制

由于多智能体系统协同控制在许多热门领域都有着广泛的应用,如卫星群的协调和控制、无人驾驶飞行器编队控制、群集控制等,所以受到了越来越多的关注.多智能体系统协同控制中一致性的研究较为广泛,一般来说,一致性的研究可以分为无领导者的一致性[1-4]和领导者追随者跟踪一致性[5-6].包含控制类似于跟踪控制,是指有多个领导者的系统对追随者设计控制协议,使它们最终趋于多个领导者形成的凸包之中[7-12].由于多智能体系统工作环境并非实时可控,系统可能会面临许多问题,比如存在通信约束、输入饱和等.文献[12]研究了间歇通信和输入饱和同时存在的情况下线性多智能体系统的包含控制,考虑追随者之间的信息交互是无向的,通信间歇是周期性的.本研究考虑智能体间信息交互是有向的(即有向拓扑),间歇通信为非周期情况下具有输入饱和的线性多智能体系统的包含控制,更具有一般性.

1 预备知识和问题描述

1.1 图论知识

本研究考虑由N个追随者和M个领导者组成的多智能体系统,用g=(ν,ε,A)表示个体间的通信拓扑.其中，顶点集ν=νF∪νL,νF={1，…,N},νL={N+1,…,N+M},边集ε⊆νF×νF∪νF×νL,记有序顶点对(i,j)为图g中的有向边,表示第j个个体可以收到第i个个体的信息.i1到ik存在有向道路是指存在有序顶点序列(i1,i2),(i2,i3),…,(ik-1,ik),其中ij∈ν,(ij,ij+1)∈ε,j=1,…,k-1.A=[aij]∈(N+M)×(N+M)表示邻接矩阵,其中aij≥0.元素aij>0当且仅当(j，i)∈ε,否则aij=0.假设图中没有自环,即aii…=0.图g的度矩阵为一对角矩阵，记为D=diag{d1，d2，…，dN+M},对角线上的元素定义为节点的入度,即第i行对角线上元素为图g的Laplacian矩阵L=D-A=[lij]∈N×N,其中满足

一般来说,有向图的Laplacian矩阵是不对称的.考虑到记为N+1，…，N+M的M个领导者没有邻居,可以将L∈(N+M)×(N+M)划分为如下形式:

式中：L1∈N×N,L2∈N×M.

1.2 问题描述

本研究考虑具有饱和输入和通信约束的线性多智能体系统的包含控制,通信约束由于通信信道的不可靠、传感器的限制等因素,智能体只能在一些不连续的时间段内与其邻居节点通信.输入饱和是指由于物理设备的限制等因素,控制输入存在界限.

多智能体系统的动力学描述如下:

(1)

(2)

式中：xi∈n,ui∈m分别为第i个智能体的状态变量和控制输入.A和B是适当维数的系统矩阵,σ(·)是饱和向量函数,定义如下:

半全局包含控制问题是指对每个追随者构造一个控制协议,使得对于任意预先给定的有界集χ∈n,只要任意的追随者和领导者的初值都在此有界集中，即xi(0)∈χ,i=1,2,…,N+M,追随者最终趋于由多个领导者形成的凸包之中.

下面引入本研究涉及的一些假设和引理：

假设1在有向图g中,任意一个追随者至少存在一个领导者到它有一条有向道路.

假设2[13]线性系统(A,B)是有界控制输入渐近零可控的,即

(1)(A,B)可镇定;

(2)A的特征值都有非正实部.

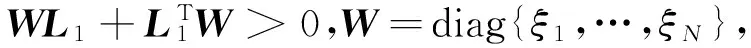
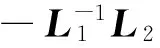
引理3[14]假设M∈N×N是一个正定矩阵,N∈N×N是一个对称矩阵,那么对∀x∈N有如下矩阵不等式成立:

λmin(M-1N)xTMx≤xTNx≤λmax(M-1N)xTMx.

引理4[15]若假设2成立，则对∀ε∈(0,1]存在唯一的矩阵P()>0,使如下代数Riccati方程成立:

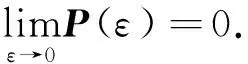
引理5对任意给定的实矩阵A=[aij]∈n×n,都存在一个正定实矩阵Q=QT∈n×n使得

ATQ+QA-βQ<0,

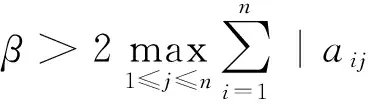
2 主要结果

对具有通信约束和输入饱和的多智能体系统利用如下算法构造状态反馈间歇包含控制协议,保证系统的低反馈增益.

算法1第1步解如下代数Riccati方程

ATP(ε)+P(ε)A-γ1P(ε)BBTP(ε)+εIn=0,ε∈(0,1],

(3)

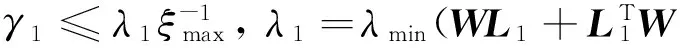
第2步对第i个追随者构造如下形式的状态反馈控制协议：

(4)

当t∈[tk,tk+δk)时,智能体可以接收到邻居的信息,即通信正常;当t∈[tk+δk,tk+1)时,智能体不能接收到邻居信息,即通信中断.其中,k∈.该算法建立在引理4的基础上保证了低反馈增益.

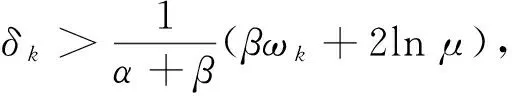
证明在状态反馈控制协议(4)下,系统(1)动力学改写为如下形式:

(5)

式中: i=1，2，…，N；k=0，1，2，….

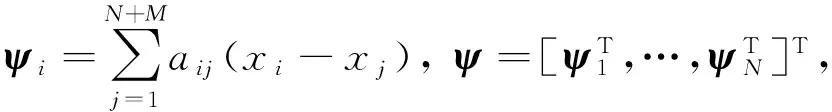
(6)

令c>0为一常数且满足:

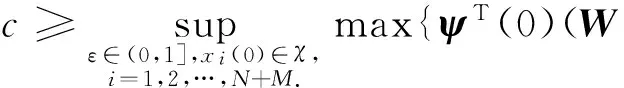
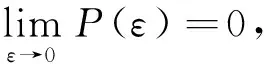
(7)

(8)

由方程(7)和(8)及ψ的定义将其写为矩阵形式：

ψ=(L1⊗In)XF+(L2⊗In)XL，

(9)

则有

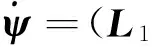
(10)

若通信中断,则有

(11)

(12)

下面分别在通信正常和中断的情况下对Lyapunov函数进行求导.

(1)当t∈[tk，tk+δk)，∀k∈时,对Lyapunov函数求导:

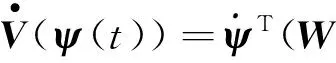
ψT(IN⊗AT-LT⊗P(ε)TBBT)(W⊗P(ε))ψ+ψT(W⊗P(ε))(IN⊗A-L1⊗BBTP(ε)ψ=

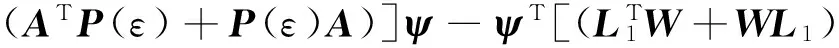
(13)

由引理3及式(3)得

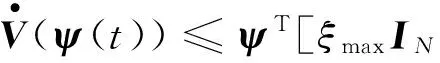
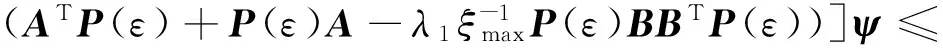
ξmaxψT[IN⊗(ATP(ε)+P(ε)A-γ1P(ε)BBTP(ε))]ψ=-εξmaxψTψ≤

-εξmaxλmin(W-1⊗P-1(ε))ψT(W⊗P(ε))ψ=

-ελmin(P-1(ε))V(ψ(t))-αV(ψ(t))，

(14)

式中:α=ελmin(P-1(ε))>0.

(2)当t∈[tk+δk，tk+1)，∀k∈时,对Lyapunov函数求导:

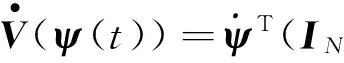
βψT(IN⊗Q)ψ=βV(ψ(t)).

(15)

由引理5易得式(15)中的不等式,其中β>0. 综上可知:

(16)

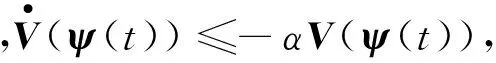
V(ψ(t1+δ1))=ψT(t1+δ1)(IN⊗Q)ψ(t1+δ1)≤λmax(Q)ψT(t1+δ1)ψ(t1+δ1)≤

μλmin(P(ε))ξminψT(t1+δ1)ψ(t1+δ1)≤μψT(t1+δ1)(W⊗P(ε))ψ(t1+δ1).

(17)

又由于

limt→(t1+δ1)-V(ψ(t))=ψT(t1+δ1)(W⊗P(ε))ψ(t1+δ1)≤V(ψ(t1))e-αδ1，

(18)

故

V(ψ(t1+δ1))≤μV(ψ(t1))e-αδ1.

(19)

V(ψ(t2))=ψT(t2)(W⊗P(ε))ψ(t2)≤λmaxP(ε)ξmaxψT(t2)ψ(t2)≤

μλminQψT(t2)ψ(t2)≤μψT(t2)(IN⊗Q)ψ(t2).

(20)

又因

(21)

那么

V(ψ(t2))≤μV(ψ(t1+δ1))eβ(t2-t1-δ1)≤μ2V(ψ(t1))eβ(t2-t1-δ1)-αδ1=V(ψ(t1)e-(α+β)δ1+β(t2-t1)+2ln μ.

(22)

令Δ1=(α+β)δ1-β(t2-t1)-2ln μ，由条件知Δ1>0.

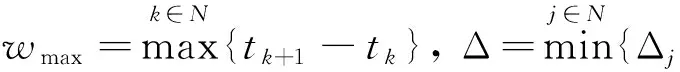
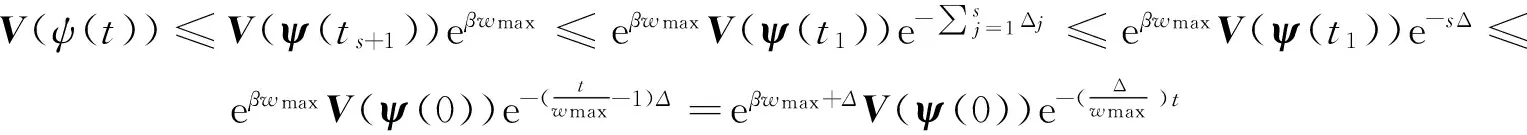
(23)

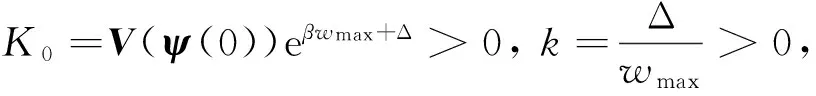
V(ψ(t))≤K0e-kt,t∈(0,∞].

(24)

从而,‖ψ(t)‖→0即

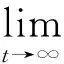
也就是说,利用算法中的反馈控制协议,追随者最终会趋于领导者形成的凸包.

3 数值仿真

考虑如下的系统矩阵：

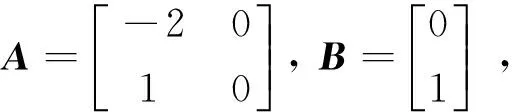
易知(A,B)可镇定且A的特征值具有非正实部.

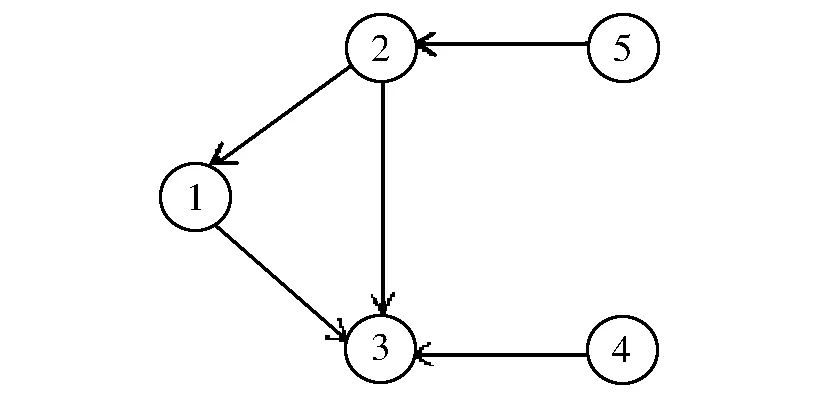
图1 多智能体系统的通信拓扑图Fig.1 Communication topology of multi-agent system

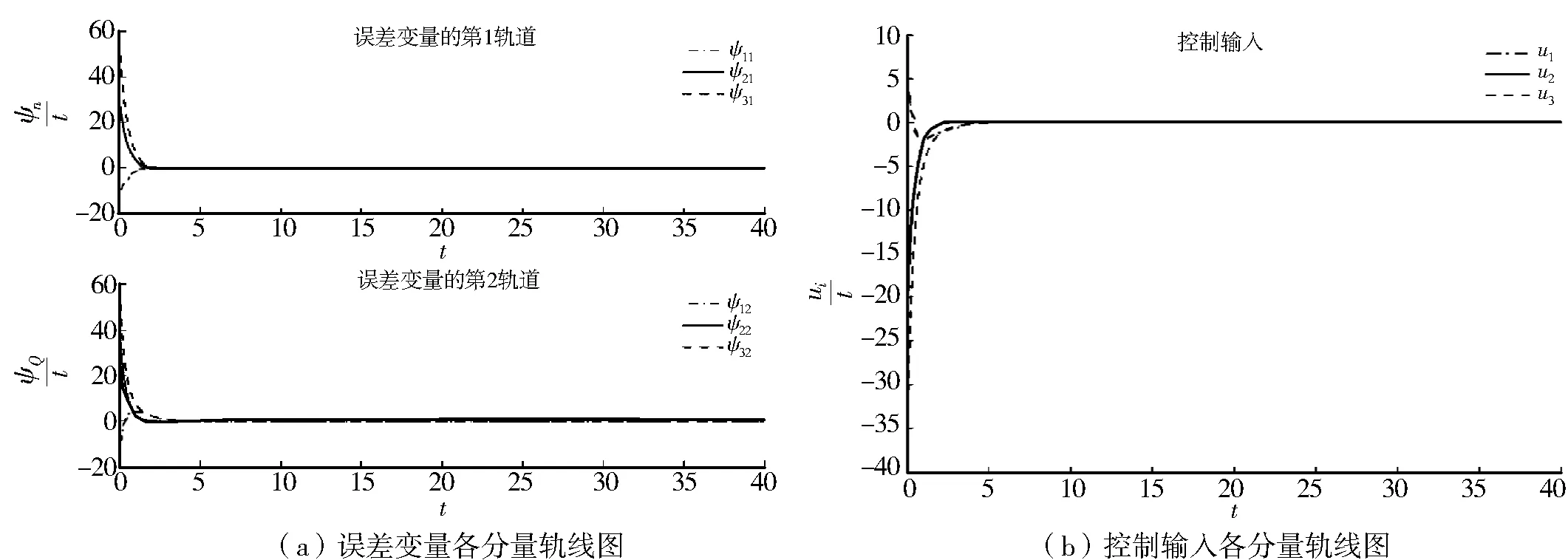
图2 当ε=0.5时,误差变量及控制输入各分量的轨线图Fig.2 ε=0.5,trajectories of error variable and control input

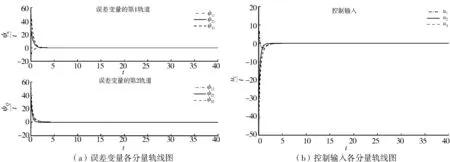
图3 当ε=0.8时,误差变量及控制输入各分量的轨线图Fig.3 ε=0.8,trajectories of error variable and control input

由图2与图3可知，若定理条件成立,控制输入的值随着ε值的减少而减少,误差变量逐渐趋于0,即所有的追随者最终趋于领导者形成的凸包之中.

4 总结

在固定有向拓扑下研究具有间歇通信和饱和输入同时存在的线性多智能体系统的包含控制问题,在系统是有界输入渐近零可控的,并且拓扑图中任意追随者至少存在一个领导者到它有一条有向道路的假设下,若持续通信时长大于某一阈值,利用代数Riccatic方程设计的低增益间歇反馈控制协议可以使系统达到半全局包含控制.

[1] WEN G,DUAN Z,YU W,et al.Consensus in multi-agent systems with communication constraints[J].International Journal of Robust and Nonlinear Control,2012,2(22):170-182.

[2] WEN G,DUAN Z,REN W,et al.Distributed consensus of multi-agent systems with general linear node dynamics and intermittent communications[J].International Journal of Robust and Nonlinear Control,2014,24(16):2438-2457.

[3] WEN G,DUAN Z,CHEN G.Distributed consensus of multi-agent systems with general linear node dynamics through intermittent communications[C]∥24th Chinese Control and Decision Conference,Taiyuan：IEEE,2012:1-5.

[4] HUANG N,DUAN Z,ZHAO Y.Leader-following consensus of second-order non-linear multi-agent systems with directed intermittent communication[J].IET Control Theory and Applications,2014,8(10):782-795.

[5] LI Z,WEN G,DUAN Z,et al.Designing fully distributed consensus protocols for linear multi-agent systems with directed graphs[J].IEEE Transaction on Automatic Control,2015,60(4):1152-1157.

[6] SU H,CHEN M,LAM J,et al.Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback[J].IEEE Transaction on Circuits and Systems,2013,60(7):1881-1889.

[7] JI M,FERRARI-TRECATE G,EGERSTEDT M,et al.Containment control in mobile networks[J].IEEE Transaction on Automatic Control,2008,53(8):1972-1975.

[8] MENG Z,REN W,YOU Z.Distributed finite-time attitude containment control for multiple rigid bodies[J].Automatica,2010,46(12):2092-2099.

[9] CAO Y,REN W,EGERSTEDT M.Distributed containment control with multiple stationary or dynamic leaders in fixed and switching directed networks[J].Automatica,2012,48(8):1586-1597.

[10]LI Z,REN W,LIU X,et al.Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders[J].International Journal of Robust and Nonlinear Control,2013,23(5):534-547.

[11]SU H,JIA G,CHEN M.Semi-global containment control of multi-agent systems with input saturation[J].IET Control Theory and Applications,2014,8(18):2229-2237.

[12]SU H,JIA G,CHEN M.Semi-global containment control of multi-agent systems with intermittent input saturation[J].Journal of the Franklin Institute,2015,352(9):3504-3525.

[13]SABERI A,LIN Z,TEEL A.Control of linear systems with saturating actuator[J].IEEE Transaction on Automatic Control,1996,41(3):368-378.

[14]HUANG L.Linear Algebra in System and Control Theory[M].Beijing：Science Press，1984.

[15]LIN Z.Low Gain Feedback[M].London：Springer，1999.

Containment control of multi-agent systems with input saturation and intermittent communications

FANG Jianyin1,XIE Xinxin1，2

(1.CollegeofScience,HenanUniversityofEngineering,Zhengzhou451191，China;2.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China)

This paper investigates containment control of multi-agent systems with input saturation and aperiodic intermittent communications,the corresponding conclusion is proved based on algebraic graph theory and Lyapunov control method. Under the assumptions that each agent is asymptotically null controllable with bounded controls and there exists at least one leader that has a directed path to each follower,low-gain state feedback aperiodic intermittent control protocol is designed according to the algebraic Riccati equation,simi-global containment control of multi-agent systems is proved theoretically if the communication duration is larger than a certain threshold. Finally,numerical simulation is given to illustrate the theoretical result.

linear multi agent systems; fixed directed topology; input saturation; intermittent communication; simi-global containment control

2016-08-20

方建印(1964-)，男，河南南阳人，教授，博士，主要从事运筹与控制研究.

TP13;TP18

A

1674-330X(2016)04-0062-07