基于泰森多边形法对南极洲平均温度测定的研究

邢晶晶，朱家明，邓 蕾，惠一奇

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)



基于泰森多边形法对南极洲平均温度测定的研究

邢晶晶，朱家明，邓 蕾，惠一奇

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

针对南极洲区域整体温度的测定，综合应用泰森多边形法建立了区域平均温度测定模型，运用了SPSS，Matlab，EVIEWS，Photoshop等软件得到了整个南极洲区域近25年的月平均温度，通过剔除季节影响因素得到了时间序列拟合函数，验证了其可行性，为测定南极洲区域整体平均温度提供了一种新方法.

泰森多边形法；南极洲；平均温度；时间序列；EVIEWS；温室效应

南极洲位于地球最南端，气候极寒干燥，生态循环缓慢且没有固定居民，是唯一未受污染的原始大陆.科学家们发现，可以通过南极洲冰层的厚度了解地球大气层的污染情况和温室效应的程度.其中，平均温度是研究气候变化和温室效应的重要指标.到目前为止，虽然已经有18个国家在南极洲建立了140多个科学考察站，但如何把这些科考站记录的温度数据综合起来得到整个南极洲大陆的平均温度，目前还没有公认的可靠方法.本研究尝试提供一种大区域平均温度测定的新方法，并就该方法的可行性进行了研究.

1 数据来源与模型假设

本研究的数据来源为文献[1]中南极洲各观测站的记录数据，提出以下假设：①忽略风对温度的影响；②海面温度与陆地温度相同；③默认温度为地表温度；④数据来源真实可靠，计算中没有错误及误差.

2 区域整体平均温度的测定

测定某地区的温度，通常情况下是通过该区域各个观测站测得的数据来估计一定范围内的平均温度.由于各个观测站点分布不均，大范围内平均温度的估计不能直接简单加总平均，要根据其他方法估计，本研究引用文献[2]中的泰森多边形法来解决此问题.

定义1泰森多边形法由美国气候学家Thiessen于1911年提出，是为了利用离散分布的气象站记录数据来计算平均降雨量的方法，原理是将所有相邻观测点连成锐角三角形，作所有三角形各边的垂直平分线，每个气象站周围的垂直平分线所围成的只包含一个点的多边形就称为泰森多边形，也称为Voronoi图或Dirichlet图，用这个点的降雨量代表整个多边形区域的降雨量.每个多边形区域面积占总区域面积的权重为该区域的降雨量加权，最后累加得到总区域的降雨量，这种方法称为泰森多边形法.公式如下：

(1)

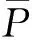
另外，泰森多边形有3个特殊的性质：①每个泰森多边形区域内有且仅有一个离散点；②每个泰森多边形内的点到此离散点的距离最近；③位于泰森多边形上的点距离其两边多边形内的离散点距离相等.根据这3个特殊性质，泰森多边形法与普通的算术平均法相比，剔除了观测点在区域内分布不均所带来的误差，文献[2]的实际应用也证明了泰森多边形法比普通算术平均法的误差更小.

泰森多边形法多用于求解区域平均降雨量，本研究将此方法延用于区域平均温度的测定.

3 南极洲1990—2015年区域平均温度的测定

3.1 数据的预处理

从British Antarctic Survey website上获取1990—2015年的地面人工观测站和地面自动观测站共113个观测站点的月平均温度数据，根据各个观测站点的经纬度在地图上找出相应位置.由于本研究着重研究1990—2015年南极洲温度变化的情况，所以将所得到的站点数据中此时间区域内数据严重缺失的站点去除.又因为地面人工观测站和地面自动观测站中一些站点的距离较近，将这些站点的数据合并以进行缺失数据的补充，最后得到符合要求的31个站点.这31个站点的数据中仍然有部分数据缺失，在保证数据完整性的前提下，利用SPSS软件中的替换缺失值功能填补缺失值.由于所得到的数据中有较多连续缺失值，所以需要利用缺失点处的线性趋势法填补缺失值.该法的原理是根据缺失值所在的整个序列构造线性回归方程，用回归方程在缺失点的预测值替换缺失值.

图1 泰森多边形图在地图上的映射Fig.1 The mapping of Voronoi Diagram-Thiessen Polygon

3.2 泰森多边形法对南极洲区域的划分

将所研究的31个站点在地图上的分布抽象到二维坐标系中，以南极点为原点，以东(西)经90°线和本初子午线(180°经线)分别为x，y轴，借助坐标转换工具[3]建立直角坐标系，按照观测站的经纬度分别确定其在直角坐标系中的坐标.根据上述泰森多边形的定义，在Matlab中画出依据31个站点位置构造出的泰森多边形，建立的坐标系在地图上的映射如图1所示.

3.3 南极洲1990—2015年各月份的平均温度

读取所建立坐标系中的31个坐标，在Matlab中分别计算各个泰森多边形的面积及其与总面积的比值，得到31个站点的权重.以月份为单位，依据公式(1)为各个站点的温度数据加权，得出总区域的月平均温度数据，见表1.

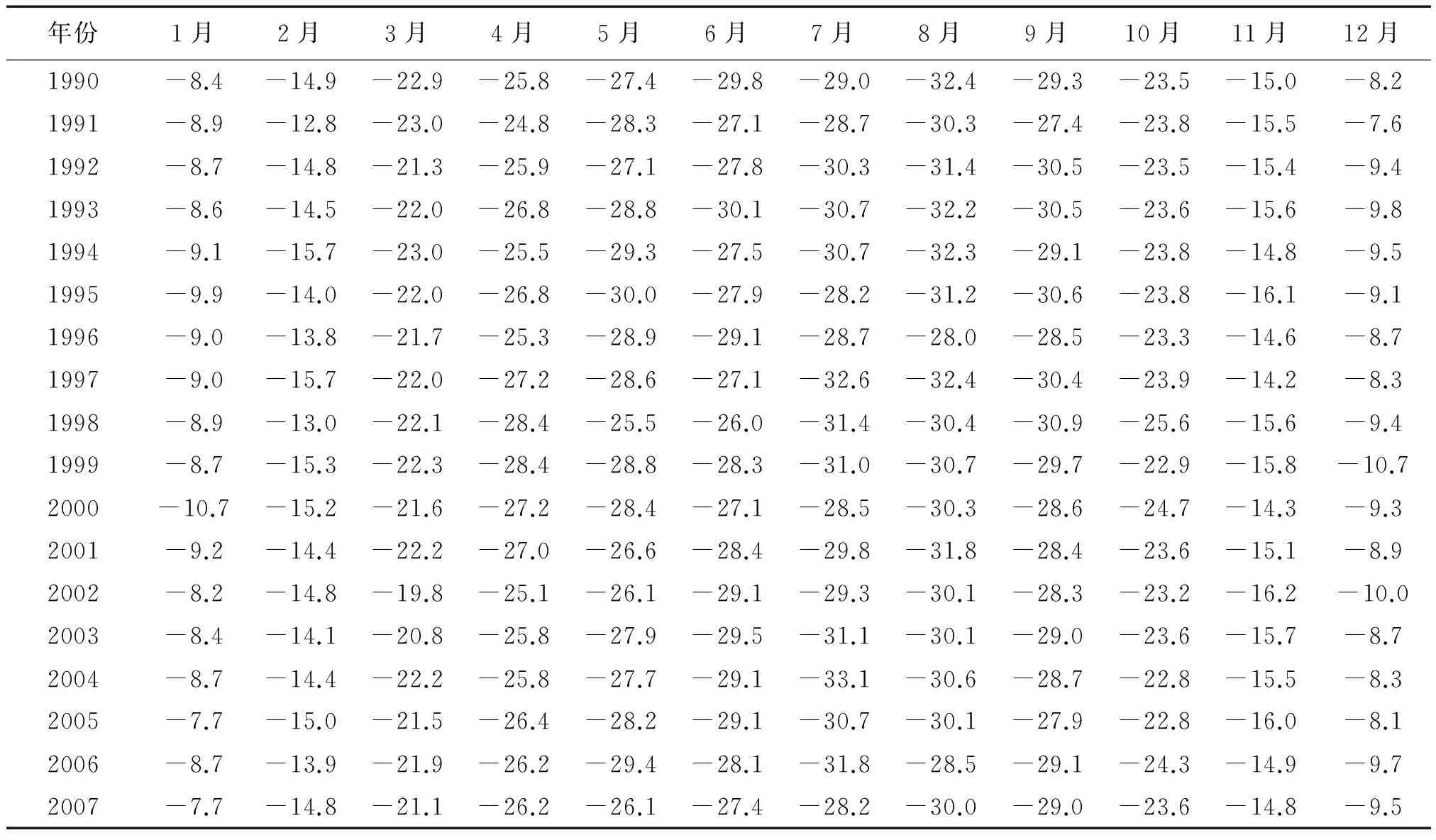
表1 南极洲各站点1990—2015年的月平均温度Tab.1 1990—2015 years average temperature of each site in Antarctica ℃

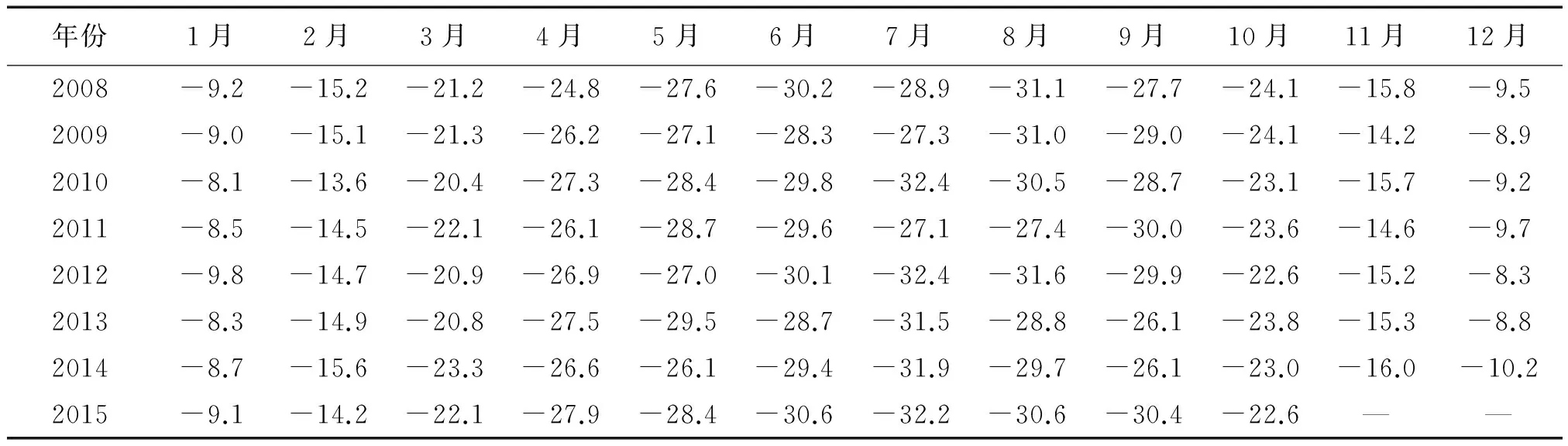
续表 ℃

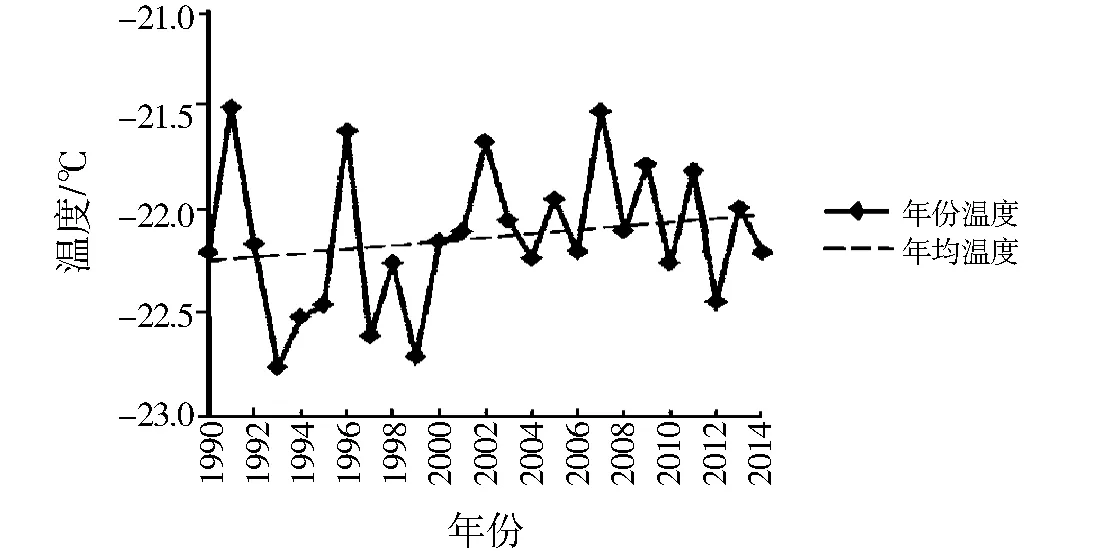
图2 年平均温度趋势Fig.2 Annual average temperature trend chart

由表1中的月平均温度数据计算出各年的平均温度，将其制成如图2所示的折线图.其中，2015年缺少11月和12月的数据,对其平均值有一定影响,故图2中只取前25年的平均温度数据.

从图2可以看出，年平均温度数据的趋势线向右上方倾斜，由此猜测年平均温度有缓慢增长的趋势.

4 南极洲区域平均温度的变化特征

4.1 确定数据的平稳性

南极洲月平均温度随时间变化且数据间相互独立，符合时间序列条件.根据应用时间序列分析[4]，将数据录入EVIEWS软件观察数据时序图与序列相关图来判断月平均温度的数据是否平稳，如图3和图4所示.

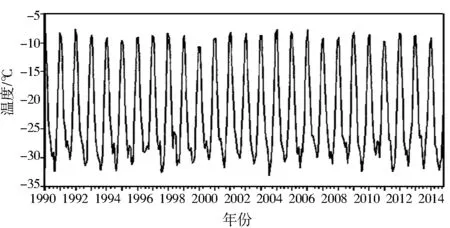
图3 月平均温度时序Fig.3 Monthly mean temperature time series

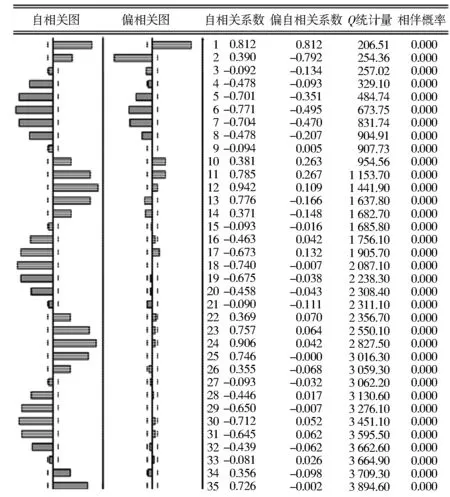
图4 月平均温度序列相关图Fig.4 Monthly mean temperature series correlation

从图4可以看出，自相关函数呈三角函数变化趋势，偏自相关函数在10倍的标准差之外才逐渐趋于0，这表明该时间序列是非平稳的，不能直接进行时间序列的模拟，数据中还存在未提取的影响因素.

4.2 剔除季节因素的影响

考虑到月平均温度数据有季节性变动，试从数据中剔除季节因素的影响.对数据使用EVIEWS软件进行季节因素的剔除，结果如图5所示.

从图5可以看出，剔除季节因素后的月平均温度数据基本符合平稳时间序列，季节因子是造成原数据不平稳的主要因素.对处理后的数据进行序列相关分析，自相关函数和偏自相关函数值均在2倍标准差之内，是平稳时间序列，表明其可以进行平稳时间序列的拟合.

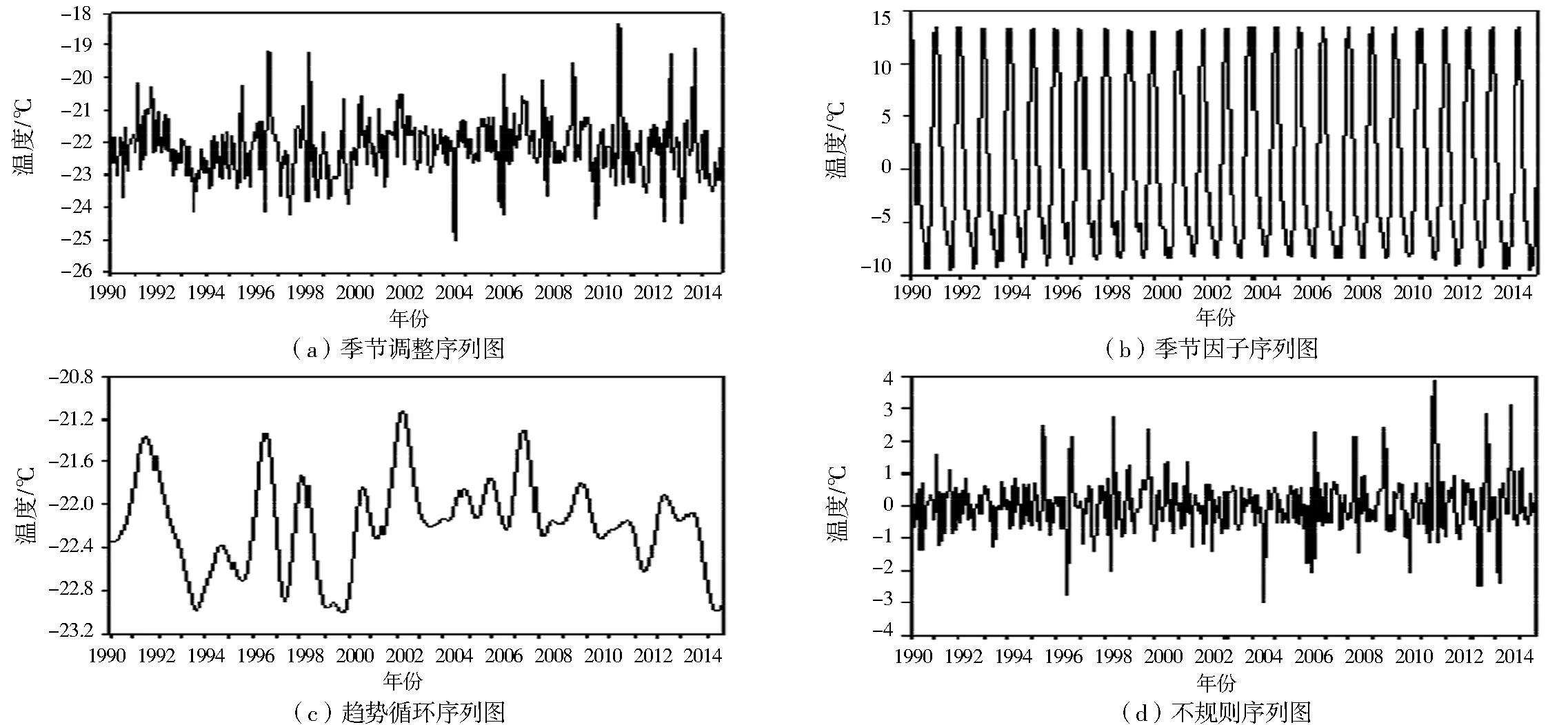
图5 季节调整后的序列特征图Fig.5 Feature of the sequence after seasonal adjustment

4.3 平稳时间序列的拟合

观察图5可发现，剔除季节因素后的数据在自相关和偏自相关系数方面均为一阶结尾，故尝试建立AR(1)模型、MA(1)模型和ARMA(1,1)模型.根据检验结果，三者的P检验值均很小，都可作为剔除季节因素后数据的模型.此处根据赤池准则和施瓦茨准则，选择AIC值和SC值更优的MA(1)模型进行拟合.

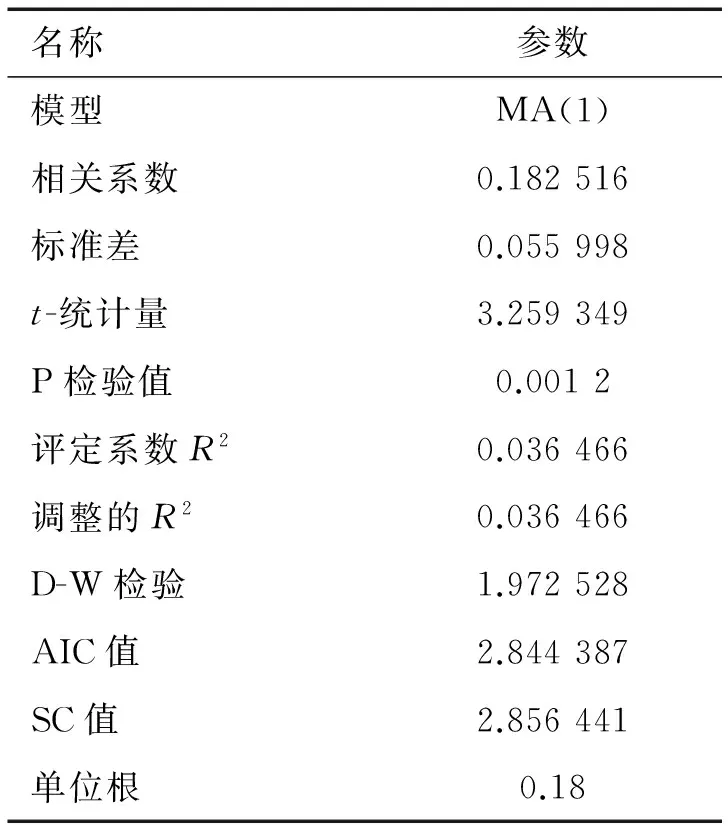
表2 标准序列最小二乘估计结果Tab.2 Least square estimation

为检验所建立的时间序列函数是否合理，对已有序列进行标准化处理并对其进行最小二乘估计(LS)，结果如表2所示.

由表2可以看出，自回归系数参数估计结果不为0，R2及调整的R2都较为合理，AIC和SC值较小且D-W值在2左右，单位根也在单位圆内，可以认为Xt平稳，可写出模型：

Xt=εt+0.182 516εt-1,εt～N(0,σ2)，

(2)

式中： εt代表白噪声过程 .

上述函数反映月平均温度随时间的增长缓慢上升，可推测南极洲的气候正在逐渐变暖，与全球气候变暖的客观事实相符.

5 结语

南极洲冰川淡水资源丰富，冰层的厚度与平均温度的变化等因素能帮助人们了解温室效应的程度，有很高的研究价值.本课题引用了应用于降水量测定的泰森多边形法，合理处理了复杂数据，并对得到的具有季节性特征的时间序列进行了加工处理，使其得以拟合为函数.最后，根据本方法得到的时间序列拟合函数表示南极洲月平均温度有缓慢上升的趋势，与全球变暖的客观事实相符.

[1] Antarctic Climate Data Results From The SCAR READER Project[DB/OL].[2016-03-08].http://legacy.bas.ac.uk/met/READER.

[2] 龙胤慧,廖梓龙.基于泰森多边形法的庆阳市面雨量计算[J].河北工程大学学报(自然科学版),2012,29(3):64-67.

[3] 李少华,刘远刚,王延忠.泰森多边形在地质数据去丛聚中的应用[J].物探与化探,2011,35(4):561-564.

[4] 王黎明,王连,杨楠．应用时间序列分析[M].上海：复旦大学出版社,2009.

2016-04-29

国家自然科学基金(11301001);安徽财经大学教研项目(acjyzd201429)

邢晶晶(1995-)，女，安徽合肥人，本科生，研究方向为应用统计.

朱家明(1973-)，男，安徽泗县人，副教授，研究方向为应用数学与数学建模.

P204

A

1674-330X(2016)04-0049-04