混合多属性决策方法在双语教学成绩评定中的应用
姜 乐,刘红彬
(1.郑州轻工业学院 数学与信息科学学院,河南 郑州 450002;2.河南财经政法大学 数学与信息科学学院,河南 郑州 450046)
混合多属性决策方法在双语教学成绩评定中的应用
姜 乐1,刘红彬2
(1.郑州轻工业学院 数学与信息科学学院,河南 郑州 450002;2.河南财经政法大学 数学与信息科学学院,河南 郑州 450046)
针对双语教学成绩评定问题,提出了一种混合多属性决策方法并给出了决策步骤.首先,计算属性权重,然后把多种形式的评价信息统一转换为二元语义,利用二元语义有序加权平均(OWA)算子集结各方案在各属性下的评价值以得到综合评价值,最后以复变函数课程双语教学成绩评定为例证明了该方法是有效的.该方法适用于百分制和语言变量混合使用的双语教学评价,可以全面评价学生的知识能力和英文水平.
多属性决策;语言变量;OWA算子;二元语义
随着我国高等教育的国际化,越来越多的本科院校采取合作办学的形式与国外大学进行交流合作,部分专业课程采用双语教学,但由于外教师资不够充分,部分课程会由具有国外留学经历的本校教师任教.这种双语教学形式大多使用英文教材和课件,使用中文讲授.这种新的教学形式使学生双语课成绩的评定与传统的中文教学有所不同,传统的中文教学成绩评定一般只根据学生的考试分数进行评价,而在双语教学成绩评价中,既要评价学生对知识的理解和掌握能力,又要评价学生使用英文进行准确交流和撰写论文的能力.因此,传统的成绩评定方式无法较好地满足双语教学的需求,需要研究新的学生成绩评定方法.
随着决策问题中所包含的不确定性及模糊性日益增加,由于决策者知识和能力的局限性,决策者往往无法提供精确数值形式的评价信息,而采用模糊信息给出评价结果,语言变量[1]是其中一种重要的模糊信息形式.由于它贴近人类的自然语言结构,也可以进行数学运算,所以得到了广泛应用,双语教学成绩评定就是一个多属性决策问题.教师选取若干个属性对每位学生的表现进行评价,最后将各属性下的评价值集结为学生的最终得分.在双语教学中,学生对知识的掌握情况可以用[0,100]的精确数值即百分制来表示,而学生的英文应用能力不适宜用精确数值来表示,如果用“很差、差、较差、一般、较好、好、很好”等语言变量来评价,则比较易于理解.一些学者利用决策理论和方法对学生成绩的评价进行了研究,李瑞兰[2]利用层次分析法研究了本科生毕业论文成绩的评价问题,张志英、曹黎霞和冯孝周[3-4]利用模糊评价模型研究了学生成绩的评价问题.但在这些方法中,成绩评定都是用精确数值形式给出的,没有考虑语言环境下的情形.对于此类精确数值和语言变量混合使用的双语教学成绩评定问题,本研究提出了一种新的多属性决策方法,将精确数值和语言变量统一转换为二元语义,进而利用OWA算子进行集结,得到学生的综合评价成绩并排序,最后通过复变函数课程双语教学成绩评定的实例验证了该方法的可行性.
1 预备知识
本部分介绍模型中所用到的概念和方法.
1.1 OWA算子
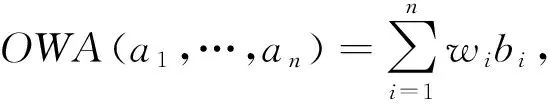
OWA算子的特点为它在集结数据之前对数据按照降序排列,算子的权重只与数据的位置有关,与数据的大小无关.OWA算子的一个重要问题是确定权重,该问题的研究成果十分丰富.Filev和Yager[6]提出了两种灵活的权重计算方法.第一种权重W=(w1,w2,…,wn)的计算公式为
w1=α,w2=α(1-α),w3=α(1-α)2,…,wn-1=α(1-α)n-2,wn=(1-α)n-1.
(1)
该权重的特点是较大数据的权重较大、较小数据的权重较小,适用于决策者具有乐观态度的情形.并且,随着n的增加,该算子的Orness测度增加,Orness测度标志OWA算子集结结果的乐观性,集结结果越大,Orness测度就越大,表示决策者越乐观.
第二种权重W=(w1,w2,…,wn)的计算公式为
w1=αn-1,w2=(1-α)αn-2,w3=(1-α)αn-2,…,wn-1=(1-α)α,wn=(1-α).
(2)
该权重的特点是较小数据的权重较大、较大数据的权重较小,适用于决策者具有悲观态度的情形.并且,随着n的增加,该算子的Orness测度减少.
这两种算子引入参数α来调节集结结果的大小,α越大,Orness测度越大,决策者越乐观.决策者可以根据自己的乐观程度选择合适的α值,所以具有较强的灵活性.
1.2 二元语义模型
定义1[7]设S={s0,s1,…,sg}为语言变量集,其中g+1为奇数,称为S的粒度,对β∈[0,g],二元语义(si,α)指的是存在一个映射Δ∶[0,g]→S×[-0.5,0.5),满足
式中:round为四舍五入函数,如round(2.1)=2,round(2.8)=3.
二元语义模型将[0,g]上的精确数值β转换为用语言变量si和[-0.5,0.5)上的一个小数α共同表示,其含义是与该精确数值β对应的语言变量为si向左(α<0)或向右(α≥0)平移|α|个单位.这样,精确数值β就可以与二元语义一一对应,意义更容易理解.特别地,对任意si∈S,其二元语义形式为(si,0).
映射Δ存在逆映射Δ-1∶S×[-0.5,0.5)→[0,g],它可以将二元语义转换为精确数值:
Δ-1(si,α)=i+α=β.
二元语义的比较法则如下:
设(si,α1),(sj,α2)为2个二元语义,
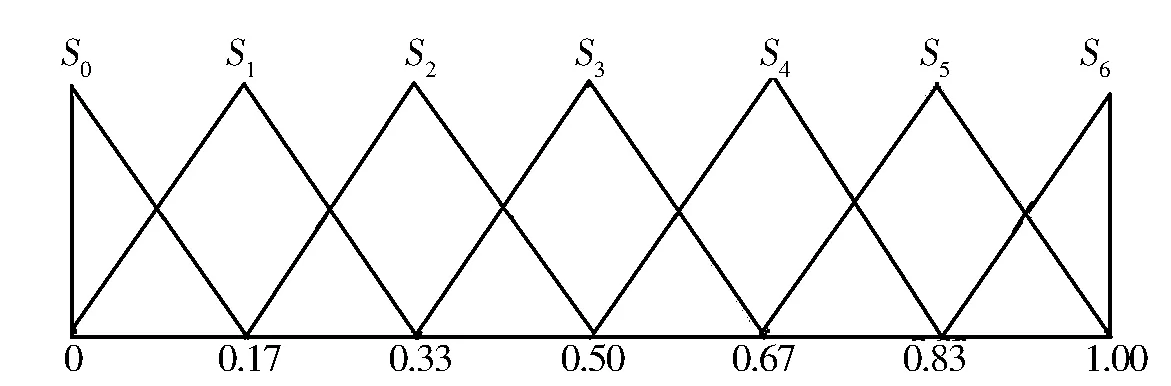
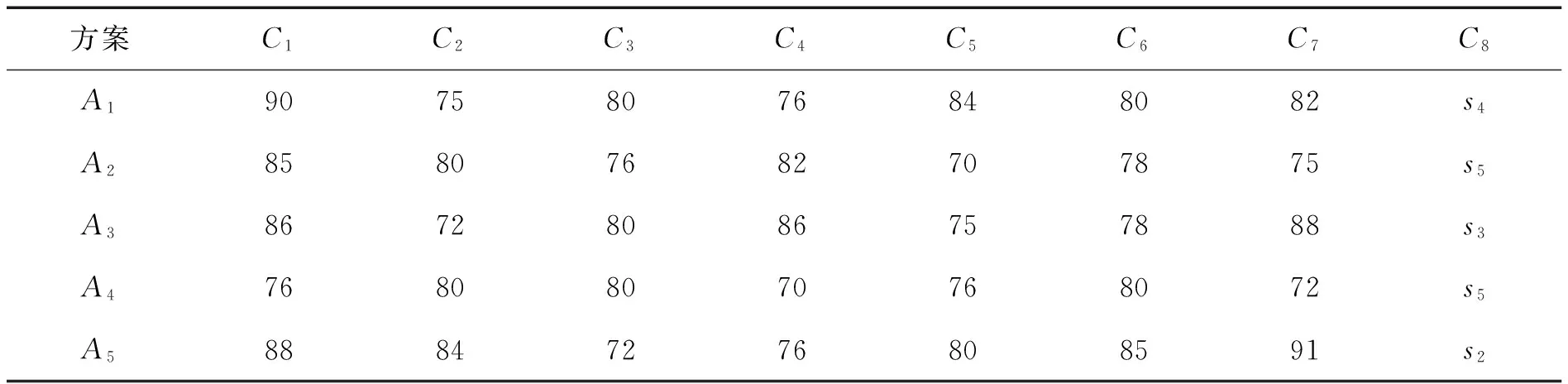
(1)若i (2)若i=j,则 ①若α1=α2,则(si,α1)=(sj,α2); ②若α1<α2,则(si,α1)<(sj,α2); ③若α1>α2,则(si,α1)>(sj,α2). 多个二元语义可以通过二元语义集结算子进行集结,这里只给出本研究中需要的二元语义OWA算子. (3) 1.3 单位区间上数值转换为二元语义的方法 Herrera等[8]提出了不同形式的信息,如单位区间上的精确数值、区间数、三角模糊数等转换为二元语义的方法,该方法适用于决策者使用多种形式评价信息的决策问题.由于精确数值和语言变量同时使用,决策过程中必须将二者统一,具体方法如下: 设S={s0,s1,…,sg}为语言变量集,其中任一语言变量si的隶属函数由三角模糊数确定,记为μsi=(αi,bi,ci),r∈[0,1],则映射f∶[0,1]→S×[-0.5,0.5)定义为 (4) ωi=μsi(r),i=1,2,…,n,即数值r属于语言变量si的隶属度为si的隶属函数在该点的函数值. 在双语教学成绩评定中,设所有选修该课程的学生为备选方案集A={A1,A2,…,An},从每一章的测验分数、期末考试分数、英文水平等方面考查学生的掌握程度,记为该问题的属性集C={C1,C2,…,Cm}.其中,学生测验和考试分数可以用百分制分数给出,而学生的英文水平不宜用百分制分数给出,故采用语言变量集给出评价信息.最后,根据学生在百分制下的成绩和语言变量集下的英文水平评价值,确定学生的总成绩并进行排序择优. 应用多属性决策方法解决这一问题的步骤如下: 步骤1 计算OWA算子的权重,即各属性的权重. 步骤2 将学生在每一属性下的百分制得分规范化,方法是将学生得分除以该属性下所有学生成绩的最大值,将学生的得分转换到单位区间上. 步骤3 将步骤2得出的单位区间上的数值利用公式(4)转换为二元语义,同时将学生英文水平的语言变量评价值写成二元语义形式. 步骤4 利用二元语义OWA算子集结各备选方案在各属性下的二元语义评价值,得到方案的综合评价值并进行排序. 图1 语言变量集S={s0,s1,…,s6}Fig.1 Set of language variables 复变函数双语课程作为数学系的一门专业课,学生学习的难度较大.为此,在教学中采取每章一测和期末考试相结合的方法,要求学生用英文答题,考查学生理解知识的程度和英文水平.全书共6章内容,取学生每章测验得分、期末考试得分、英文水平等8个属性作为该问题的属性,即C={C1,C2,…,C8}.取参加学习该门课程的全体学生为备选方案,为简明起见,以5名学生为例,即备选方案A={A1,A2,…,A5}.测验和考试成绩采用百分制计分,英文水平采用语言变量集S={s0,s1,…,s6}={很差,差,较差,一般,较好,好,很好}给出,其隶属函数如图1所示.学生的成绩如表1所示. 表1 学生成绩评价表Tab.1 Student’s score evaluation 利用前面所述的步骤解决此问题. 步骤1 由于n=8,若采用算术平均,则各属性权重均为0.125.基于鼓励学生的目的,对学生的较好成绩赋予较高的权重,较低的成绩赋予较低的权重,同时对学生的最差成绩也适当考虑,以督促学生尽快改进.为此,采用第一类权重公式(1)且取参数α=0.3,得到各属性的权重向量为W=(0.30,0.21,0.15,0.10,0.07,0.05,0.04,0.08).很容易看出,该权重中较小数据的权重较小且最小数据权重略大于次小数据,表示对最小权重也给予了一定的重视.在该权重下,集结结果大于算术平均的结果,可以看出决策者持乐观态度. 步骤2 对于前7列,每一列值都除以该列的最大值,使所有数值规范化.如第1列的最大值为90,该列数值除以90后,得到的规范化结果为(1,0.94,0.96,0.84,0.98)T. 步骤3 利用公式(4)将上一步中规范化的单位区间内数值转换为二元语义,第8列数据直接转换为二元语义,结果如表2所示. 表2 转换后的二元语义评价值Tab.2 Evaluation of daul semantie value after transformation 以方案A1在属性C1下的评价值为例给出计算过程.方案A1在属性C1下的评价值规范化后为0.94,很容易看出语言变量s0,s1,…,s4的隶属函数在0.94处为0,即ωi=0,i=0,1,…,4.语言变量的隶属函数在0.94处为ω5=1-(0.94-0.83)÷0.17=0.35,语言变量s6的隶属函数在0.94处为ω6=(0.94-0.83)÷0.17=0.65,利用公式(4)可得0.94转换为二元语义的结果为 步骤4 利用二元语义OWA算子集结每位学生在各属性下的二元语义评价值,得到综合评价值((s6,-0.297),(s6,-0.394),(s6,-0.389),(s6,-0.467),(s6,-0.410)). 以方案A1为例,具体的计算过程为 F((s6,0),(s5,0.35),(s6,0),(s5,0.29),(s6,0),(s6,-0.35),(s5,0.41),(s4,0))= Δ(0.30×6+0.21×6+0.15×6+0.10×5.65+0.07×5.41+0.05×5.35+0.04×5.29+0.08×5)=(s6,-0.297). 由上述综合评价值可得学生成绩排序为A1≻A3≻A2≻A5≻A4,即学生A1的成绩最好. 本研究给出了一种同时使用百分制和语言变量来评价学生双语课成绩的多属性决策方法.考虑到双语教学不但要求学生掌握知识,还要求学生规范使用英文、掌握专业术语,所以在评价学生成绩的过程中不但要评价考试成绩,还要考查英文水平,考试成绩通常用百分制给出,而英文水平适宜用语言变量进行评价.因此,本研究提出的方法能够更好地适应双语教学的要求,计算程序简便,易于在计算机上实现,模型中的集结算子权重计算也比较灵活,决策者可以根据自己的偏好选择合适的参数,使集结结果反映决策者的态度和偏好,该方法对双语教学成绩的评定是一个有益的探索. [1] ADEH L.The concept of a linguistic variable and its applications to approximate reasoning[J].Information Sciences,1975(8):199-249. [2] 李瑞兰.层次分析法在毕业设计(论文)成绩评定中的应用[J].长春工程学院学报(社会科学版),2011,12(4):156-158. [3] 张志英.模糊评价法在本科毕业设计成绩评定中的应用[J].浙江理工大学学报,2011,28(3):467-470. [4] 曹黎侠,冯孝周.考查课成绩评定的模糊综合评价模型[J].西南民族大学学报(自然科学版),2010,36(3):325-329. [5] YAGER R.On ordered weighted averaging operators in multicriteria decision making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,18(1):183-190. [6] FILEV D,YAGER R.On the issue of obtaining OWA operator weights[J].Fuzzy Sets and Systems,1998,94(2):157-169. [7] HERRERA F,MARTINEZ L.A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Fuzzy Systems,2001,8(6):746-752. [8] HERRERA F,MARTINEZ L,Sánchez P J.Managing non-homogeneous information in group decision making[J].European Journal of Operational Research,2005,166(1):115-132. The application of hybrid multi-attribute decision making method to performance evaluation in bilingual teaching JIANG Le1,LIU Hongbin2 (1.SchoolofMathematicsandInformationScience,ZhengzhouUniversityofLightIndustry, This paper introduces a hybrid multi-attribute linguistic decision making method for students’performance evaluation in bilingual teaching. The decision making steps are as follows: firstly,the weights of attributes are calculated. Secondly,multi-types of assessments are transformed into linguistic 2-tuple. The assessments of alternatives with respect to different attributes are then aggregated by using the linguistic 2-tuple OWA operator. Finally,an example of students’performance evaluation in bilingual teaching of complex variables is given to illustrate the feasibility of the method. This method is suitable to be applied to performance evaluation in bilingual teaching,in which scores and linguistic terms are used simultaneously,and it can evaluate students’knowledge and linguistic level in a comprehensive way. multi-attribute decision making; linguistic term; OWA operator;linguistic 2-tuple 2016-04-06 国家自然科学基金项目(11326161);河南省教育厅高等学校重点科研项目(15A630011,16A630038);郑州轻工业学院博士科研启动基金(BSJJ2013053) 姜乐(1985- ),女,辽宁本溪人,讲师,博士,研究方向为模糊数学及决策分析. 刘红彬(1982-),男,河南濮阳人,讲师,博士,研究方向为多属性决策理论与方法.E-mail:Liuhongbin92@126.com. C934 A 1674-330X(2016)04-0074-05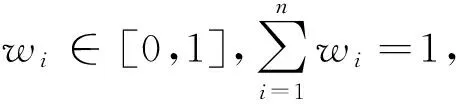

2 双语教学成绩评定的多属性决策模型
3 算例分析

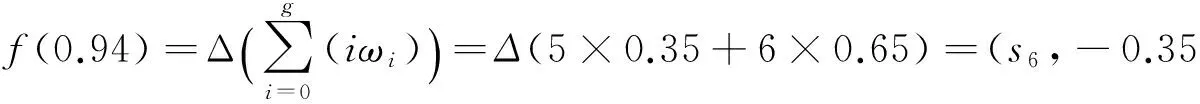
4 结论
Zhengzhou450002,China; 2.SchoolofMathematicsandInformationScience,HenanUniversityofEconomicsandLaw,Zhengzhou450046,China)

