基于多元表征理论下的数学教学实践与思考
江苏省常熟理工学院 (215500)
盛一凡*
江苏省常熟市浒浦高级中学 (215512)
殷伟康
基于多元表征理论下的数学教学实践与思考
江苏省常熟理工学院 (215500)
盛一凡*
江苏省常熟市浒浦高级中学 (215512)
殷伟康
所谓“多元表征理论”即是更加强调数学问题心理表征的多元性,强调数学问题表征不同方面的相互渗透与必要互补.更为重要的是,“多元表征理论”突出强调了数学问题的心理表征往往包含多个不同的方面或成分,这些成分对于数学问题的正确理解都具有重要的作用;另外,与片面强调其中的某一成分相对应,我们又应更加重视这些成分之间的联结与相互转换,进行多元表征,发现解题思路,有助于学生不断完善认知结构,更有利于培养学生的数学表达能力,提升数学素养.
1.加强数学问题表征的转换训练,提高数学表达能力
著名心理学家西蒙指出:“表征是问题解决的一个中心环节,它说明问题在头脑里是如何呈现的,如何表现出来的.”因而,在数学概念和数学公式的教学过程中要注重引导学生把握表征取向,加强数学问题表征的转换训练,创设问题情境,使问题表征尽可能和数学概念、数学公式相匹配,加深对概念、公式的理解.

基本不等式不同于方程、函数这样的以等式变换为主要特征的数学内涵,出现了一种更加灵活的数学现象:研究两个变量组成的代数式之间的不等关系.两个变量,两个代数式,一个恒成立的不等关系式.这种新型的数学模式对学生来说是陌生的,不少学生的思维可能仍然囿于原有的思维模式之中,此时需要教师有意识地指导学生进行问题表征转换训练,展示其不同的表征形式,让学生了解数学问题表征的特点和主要表征形式,并逐步掌握问题表征的基本要领,促进学生建立数学公式的多元表征和深层次理解基本不等式.
(1)语言表征:两个正数的等差中项不小于它们的等比中项.也可表述为两个正数的算术平均数不小于它们的几何平均数(当且仅当两个正数相等时,这两种平均数相等).让学生通过用简洁准确的语言表述公式,这不仅有助于学生理解基本不等式,而且有利于提高学生运用数学语言表达交流能力和数学素养.
(3)操作表征:利用Excel 进行现场操作,让学生分别取值计算两个正数的等差中项、等比中项,通过对比计算结果,发现两个代数式之间的关系,由此猜想出基本不等式.这样有利于学生进行归纳、概括与猜想活动,提供具体和易于理解的直接经验.

“商品打折”问题的设计,把生活中的鲜活题材引入课堂教学,赋予“基本不等式”以新的活力,让学生从数学角度观察日常生活中的现象,经历抽象提炼数学模型和数学应用的过程,培养学生数学素养.

图1

试指出图中哪条线段分别是a,b算术平均值和几何平均值?能否比较他们的大小关系?
借助学生熟知的几何图形,引导学生从几何图形中抽象出基本不等式,使学生体会数形结合的思想,领悟数学韵味,同时也使得学生理解很多看似抽象的代数不等式都源于几何图形,体会从形到数的转化.
通过数学问题表征的转换训练,帮助学生建立起各种表征方式之间的联系,不仅可以不断提升学生对数学问题的各种表征进行系统内转换和系统间的转译能力,提高多元表征能力,而且还能使学生对数学问题的表征形成直觉和积累经验,从而加深对问题的理解和数学表征的体验,领悟其本质,提高数学表达能力.
2.创设问题多维表征的交流平台,提高问题表征能力
数学问题的表征模式是由数学概念、命题、算法与策略经验等基本模式产生的心理图式.数学概念、命题、算法等基本模式具有对数学问题转译方式的多样性,从而形成了表征方式的多样性,每一种表征中的联结词都包含着解题策略和方法.问题多维表征是解题思路产生的源泉,因而在数学教学过程中,教师要善于运用启发性提示语:“你能否根据自己的联想,尝试用适当的方式将问题进行重新表征?”“在遇到困难的情况下,你能否变换问题的表征方式,调整解题的思维方向?”激活学生原有的知识块,产生联想,诱发学生进行多维表征.
问题2(2015年江苏省高考试题第10题)在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为________.
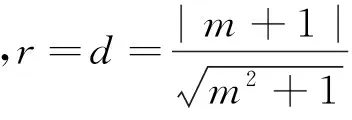

表征2:(函数模式)令m+1=t,则t≠0,

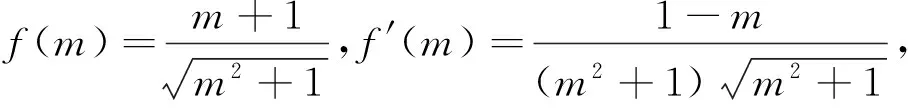
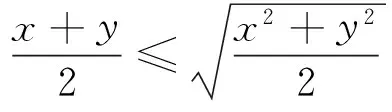
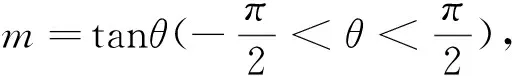


通过不同表征方式的交流,处于不同层次的学生将会对自己的表征方式进行同化和顺应,将会改进、完善已有信息表征方式,提升问题表征的质量,积累问题表征的经验.
3.通过问题表征系统的建构与分析,形成解题思维走向
当数学问题中信息较多时,则容易产生干扰交错的现象,很多学生常常因此出现思维不畅,无法顺利解答.通过建构表征系统,可以理顺信息间的逻辑关系和因果联系,进而帮助学生形成清晰的解题思维走向.
问题3(2016年江苏省高考试题第14题)在锐角三角形ABC中,sinA=2sinBsinC,则tanAtanBtanC的最小值是________.
通过建构表征系统,本题信息:①锐角三角形ABC;②sinA=2sinBsinC;③tanAtanBtanC的最小值.引导学生从中提取出核心信息“sinA=2sinBsinC”,据此聚拢所有信息,逐步把握问题的本质,最终形成条件与目标之间的思维通道.

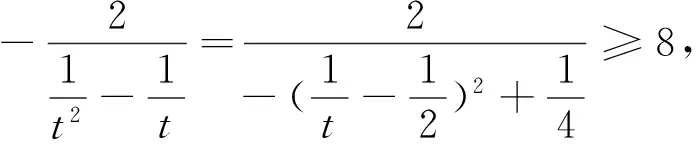
tanAtanBtanC的最小值是8.
思维走向2:(以地位关系为起点)将核心信息②化解为tanB+tanC=2tanBtanC,据此,联想三角形中重要结论tanA+tanB+tanC=tanAtanBtanC,从整体思考,运用基本不等式即可.由信息①得tanA>0,tanB>0,tanC>0,tanAtanBtanC=tanA+tanB+tanC=tanA+2tanBtanC
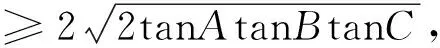
通过建构表征系统,确定核心信息,理顺信息之间的关系,按照不同的起点形成相应的思维走向.
4.学会选择合理的模式表征的方法,简约解题思维过程
数学问题的解决的前提条件是对问题进行合理表征.辨别问题的类型,根据问题的结构特征,联想已有的模式结构特征,进行模式识别(包括模式特征、适用条件、模式的本质和功能),再进行问题表征.问题表征是否适宜,直接影响到数学问题解决的难易和快慢.

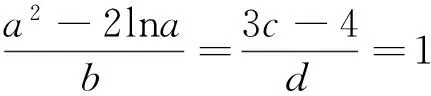
适当的图形表征有助于问题的形象直观思考,引导学生对问题深层次结构特征的正确表征,更容易激活问题图式,从而顺利解决问题.合理的模式表征有助于简约问题解决的思维长度,快速解决问题.
总之,在教学中要创设展示学生问题表征的时机,引导学生深入问题内部,建构恰当的信息表征系统和高质量的尽可能多的图式表征,让学生积累丰富的问题表征的方式和经验,有效地提高学生理解问题和问题表征能力.
[1]殷伟康.培养学生数学问题表征能力 “三部曲”[J].中学数学(高中版),2013(7):65-67.
[2]陈勇,丁益民.解题活动中表征系统的建构与分析[J].中学数学(高中版),2015(1):23-24.
[3]陆学政.“多元表征理论”指导下的“数列概念”教学[J].中学数学教学参考,2012(4):10-13.
[4]王思俭.2015年高考数学江苏卷特点回眸[J].中小学数学(高中版),2015(7-8):119-122.
* 作者为2015级经济统计学专业在读生.

