处理含双参平面向量问题的五大策略

江西省信丰中学 (341600)

张二生

处理含双参平面向量问题的五大策略

江西省信丰中学 (341600)

张二生

平面向量是高中数学知识的一块重要内容，它集数与形于一体，与代数、几何以及三角函数等数学知识紧密地联系在一起，它作为高考的重要考点，经常出现在选择与填空的压轴题中，尤其是含双参的平面向量问题，近几年高考命题的频率比较高，考生在处理这类问题时，经常感到无助，不知从何处找到切入口.作为教学一线的高中数学教师，笔者对近几年各个省份有关含双参平面向量问题的高考题与模考题进行了系统的整理，归纳出了处理这类问题的五大策略，供大家参考，以飨读者.

策略一、直角坐标法

直角坐标法是处理平面向量问题的主要方法，只要能够建立直角坐标系，把点的坐标表示出来，则向量的坐标就可以求出来，从而含双参平面向量问题就可以用坐标公式解决.

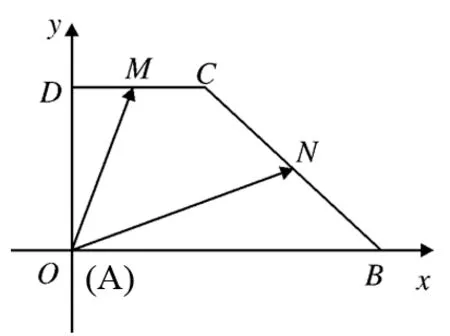
图1

策略二、向量基底法

若问题不适宜建立直角坐标系解决，则不妨尝试向量基底法，它也是处理含双参平面向量问题的主要方法，所谓向量基底法就是根据平面向量基本定理，选择好向量基底，再把题目所给向量全部用基底表示出来，最后翻译题目所给的向量关系.

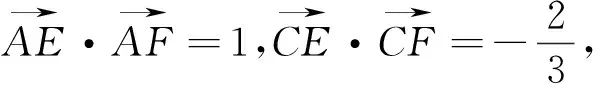
图2

策略三、三角代换法

当平面向量语言所表述的几何元素为点，且这样的点具有明显的圆(圆弧)的几何特征，那么我们就可以根据三解函数的定义，把圆(圆弧)上的各个点用坐标表示出来，即相应向量的坐标就出来了，最后代入题设中的向量关系式，问题就得以解决.

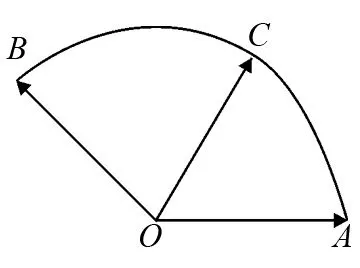
图3

解:如图3所示，以OA所在直线为x轴，以垂直于OA的直线为y轴，点O为原点，建立平面直角坐标系xOy.

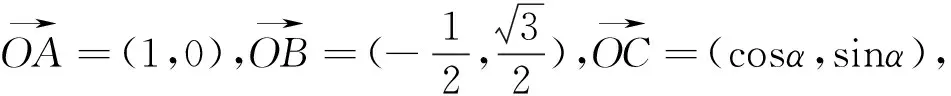
策略四、构造线性规划模型

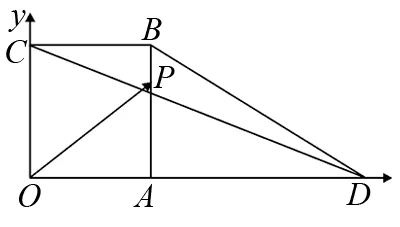
图4

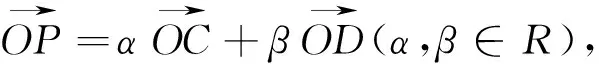
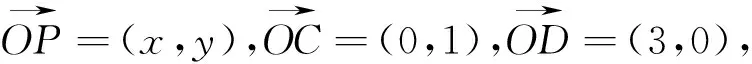
评注：本题明为几何问题，实为线性规划.通过建立平面直角坐标系，假设动点P的坐标，利用已知向量的等价关系，把两个参数α,β用未知量x,y表示出来，从而构建出目标函数，进而转化成线性规划问题来求解.

策略五、补形法

利用补形法来解决平面向量问题的实质是根据平面向量的基本定理及平行四边形法则，构造平行

四边形，结合共线向量定理与解三角形的相关知识对问题加以解决.

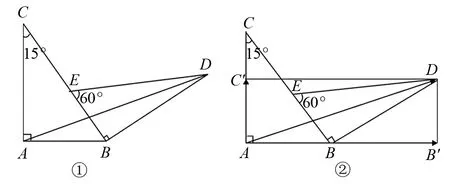
图5

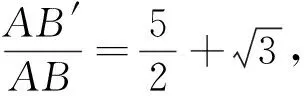
综上，含双参平面向量问题，题目涉及的知识较多，解题的方法较灵活，上述介绍的几种方法是比较常用的，但由于问题的形式千变万化，考题也常考常新，所以还需要我们不断地去领悟、体会和总结.