基于PRISM的山地环境大气湿度的空间插值

蒋育昊，刘鹏举，夏智武，贾道祥，闫 明

(中国林业科学研究院资源信息研究所，北京100091)

基于PRISM的山地环境大气湿度的空间插值

蒋育昊，刘鹏举，夏智武，贾道祥，闫 明

(中国林业科学研究院资源信息研究所，北京100091)

基于PRISM方法设计开发了山地大气湿度空间插值模型，选取北京西部山区作为试验区域，利用气象科学数据共享平台上36个台站资料和1∶25万DEM数据生成年、月、日3个时间尺度下大气相对湿度的栅格信息.采取站点交叉验证的方式对插值结果进行精度评估，并与反距离加权、克里金等其他空间插值方法的插值精度进行比较.结果表明:基于PRISM模型的大气湿度空间插值模型适合模拟北方山地的大气湿度分布场，年平均相对湿度和月平均相对湿度的插值精度比较高；与考虑空间距离或者空间距离结合海拔的其他插值方法相比，该模型插值精度有了较大提高.

大气湿度；空间插值；PRISM；加权线性最小二乘回归

大气湿度是指近地面大气层空气中水分的含量，常用水汽压、露点、相对湿度等指标来衡量[1].大气湿度是重要的森林环境要素之一，它一方面调节着植物生理生态和水分的平衡过程，对森林植被的光合作用、蒸腾作用等有重要影响[2]；另一方面它也调节着土壤与森林可燃物的含水量，是林火预测的重要参考指标[3－6].同时，在林木生长模拟模型、林区水文－生态过程模型、林火发生及蔓延模型等研究中，山地大气湿度均是其输入因子[7].由于受到当前站点分布和山地条件的影响，大范围的湿度场信息往往难以直接获取，所以依靠插值方法得到高分辨率的山地大气湿度分布场网格数据是如今农林生产与科学研究的迫切需求.

目前湿度要素空间分布数据的来源途径主要有两类:一类是基于遥感影像数据进行空间场反演[8]，另一类是基于地面气象台站的观测数据进行空间插值[9－10].何杰颖等[11]利用地基和星载微波辐射计数据反演大气湿度.刘旸等[12]基于高光谱分辨率遥感影像，使用人工神经网络法繁衍了晴空大气湿度廓线.李正泉等[13]利用GIS技术，结合DEM和气象站点数据建立了东北地区分辨率为1 km2的湿度分布图.胡丹桂等[14]以东三省为例，结合气象数据，采用克里金插值方法估计了试验区的空气湿度分布情况.随着地面气象台站自动化程度的不断提高和站点密度的不断增加，空间插值成为获得高分辨率湿度要素空间信息的主要方式[15].常用的空间插值方法有2种:(1)基于数学函数的确定性插值方法，包括反距离加权法、多项式法、样条函数法、径向基函数法等；(2)基于地统计模型的插值方法，包括普通克里金法、简单克里金法、泛克里金法、趋势面法等[16].上述空间插值方法主要的不足之处是单纯考虑空间距离因素，忽略地形地貌的影响；适用于大尺度空间，不适用于小尺度复杂环境；模型插值环境适应性差，难于推广[17－18].

针对以上问题，国外研究者结合了空间插值原理，综合考虑空间距离和局部地形地貌建立MTCLIM、DAYMET、PRISM等模型，用于复杂环境气候的模拟[19－21].坡面回归插值模型(parameter-elevation regression on independent slopes model，PRISM)是一种基于地理空间特征和回归统计方法生成的气候空间分布场模型.赵登忠等[22]最早引入PRISM模型进行气温和降水的空间内插，研究结果表明PRISM方法比其它内插方法能够更加精确地表达气象要素的空间分布，更适用于地形复杂地区气象要素的空间插值.夏智武等[23]也利用PRISM模型对北京西北山区进行了山地日气温插值研究，得到了良好的结果.目前PRISM模型研究多集中于大尺度空间上气温和降水的气象制图应用，大气湿度分布模拟方面的研究尚未见报道[24－25].

本研究基于PRISM空间插值的理论与方法，探讨海拔、坡向等地形因子对大气相对湿度的影响，建立小尺度的山地环境相对湿度空间插值模型，并通过实测数据验证该模型的有效性.

1 PRISM模型

PRISM模型是由美国气象学家Christopher Daly首先提出[26]，是基于独立坡面的气象－海拔回归模型.该模型兼顾独立坡面规律和局部地形的影响，将高程作为影响区域内气象要素空间分布的最主要因素，综合考虑高程、距离、坡向、坡度、垂直分层、距离海岸线的远近等因子的影响，能够有效地反应小尺度复杂空间上气象要素的分布特征[27－29].模型根据插值区域对主要影响因子的权重进行调整，比如沿海平原地区考虑海洋距离的影响，复杂山地环境则考虑坡向的影响.模型有2个主要特点:一是将坡向作为地形趋势面划分的依据；二是模型插值是通过移动窗口技术得到本地化的气象要素垂直变化率.PRISM模型主要有独立坡面、加权回归、综合权重3个模块.

1.1 单一坡面原理

具有相同坡向的连续空间区域称为地形趋势面或者独立坡面.在地形趋势面上，气象要素随海拔的变化呈规律分布.基于气象台站的海拔，采用线性函数估计独立坡面上任何位置的气象值.趋势面上气象要素线性回归预测公式表示如下:

式中，β1是台站资料统计回归后的气象垂直变化率；β0是台站资料统计回归后的虚拟海平面气象值；X是输入海拔；Y是气象预测值；β1m、β1x是β1取值范围的下限和上限，β1范围的设置要依据插值区域的实际情况而定.

1.2 局部线性加权回归

在插值过程中为了反映海拔对气象要素的影响，模型采用一致的垂直变化率.PRISM模型认为气象要素垂直变化率是随着环境而变化的，需要在每个独立坡面计算当地的垂直变化率.通过控制地形趋势面的分辨率选择合适的尺度，选中足够多的位于同一坡面的台站，根据选中台站的综合权重进行线性加权回归，并计算预测模型中的2个参数.计算公式如下[30]:

式中，n是窗口内样本站点数目；β1是局部加权回归的垂直变化率；β0是局部加权回归的海平面气象值；Wi是第i站点的综合权重大小；yi是第i站点的气象要素值；xi是第i站点海拔.

1.3 综合权重计算

气象要素不仅受到海拔的影响，还受到坡向、坡度等地形要素以及其他因素的影响.PRISM模型通过综合权重函数来反映不同类型的气象站点对回归过程的影响，与待预测点相似度高的气象站点被赋予较大权重.综合权重计算函数中需要输入坡向、坡度、海拔、离海洋的距离，以及空间距离等地形因子，由于本研究针对山地小环境进行预测，不考虑离海洋的距离、垂直分层等因子，仅选择空间距离、海拔、坡向3个因子.调整后的综合权重函数计算公式表示如下:

式中，W表示综合权重函数；W(d)、W(z)、W(f)分别是空间距离权重函数、海拔距离权重函数、坡向权重函数.参数Fd、Fz、a、b、c分别设置为0.8、0.2、2、1、1.Δf是站点与目标栅格方位差值的绝对值(坡向方位最大差值为4个方位点，最小差值为0)，△z是栅格与站点间的高程差的绝对值，△zm、△zx分别为最小、最大高程差，a是距离权重指数，b是一维指数，c是坡向权重指数，d是站点与栅格的水平距离.

2 模型的实现及验证

2.1 PRISM模型的实现

根据PRISM模型原理与方法设计并开发了基于台站输入数据和DEM数据的山地大气湿度空间插值模型，通过该模型可以得到北京西部山地区域的大气相对湿度空间分布信息.模型通过输入不同时间尺度的数据源，分别得到年、月、日3个时间尺度的相对湿度空间分布结果.

大气湿度空间插值模型设计为6个模块:数据读取模块、数据写入模块、移动窗口模块、加权回归模块、插值预测模块、交叉检验模块，其中移动窗口、加权回归、插值预测是关键模块.移动窗口模块的功能是搜索窗口范围内与待插值栅格单元处于同一地形趋势面的气象站点数目，并记录下各个选中站点的所有信息.加权回归模块的功能是通过坡位、坡向、海拔、距离等因素计算气象站点的综合权重大小，然后基于被选中站点的综合权重和湿度、海拔信息，通过加权最小二乘回归得到本地化垂直变化率.插值预测模块的主要功能是设定地形趋势面的最小站点数目阈值、窗口扩展的步长以及回归分析失效情形下的系统默认值，最后根据垂直变化率和虚拟海平面的相对湿度对栅格单元进行相对湿度预测.

基于Visual Studio 2010开发环境和GDAL动态库，依据数据预处理的结果编写数据输入接口，设置模型参数和专家知识预定值范围，依据系统设计完成各个模块的代码编写.在VS2010平台上调试相对湿度空间插值程序直至成功，依次输入预处理数据可以得到研究区域上各个时间尺度下大气相对湿度分布图.当利用程序调用交叉检验模块时，程序则输出研究区内各个台站之间的交叉检验结果.

2.2 试验的验证

2.2.1 数据来源及预处理 本研究采用的地形数据包括:北京西部山区1∶25万DEM数据，空间分辨率100 m×100 m；北京西部山区坡向栅格数据，分辨率1 km×1 km.观测数据来源于国家气象科研数据共享平台，包括北京西部地区36个自动气象站点，时间为2012年1至12月每天0时到24时整点时刻站点的气象观测数据，记录气象因子(温度、相对湿度、降雨、风速、风向等)及站点信息(代码、经度、纬度、坡向、高程).各类插值模型所用到的站点信息如表1所示.

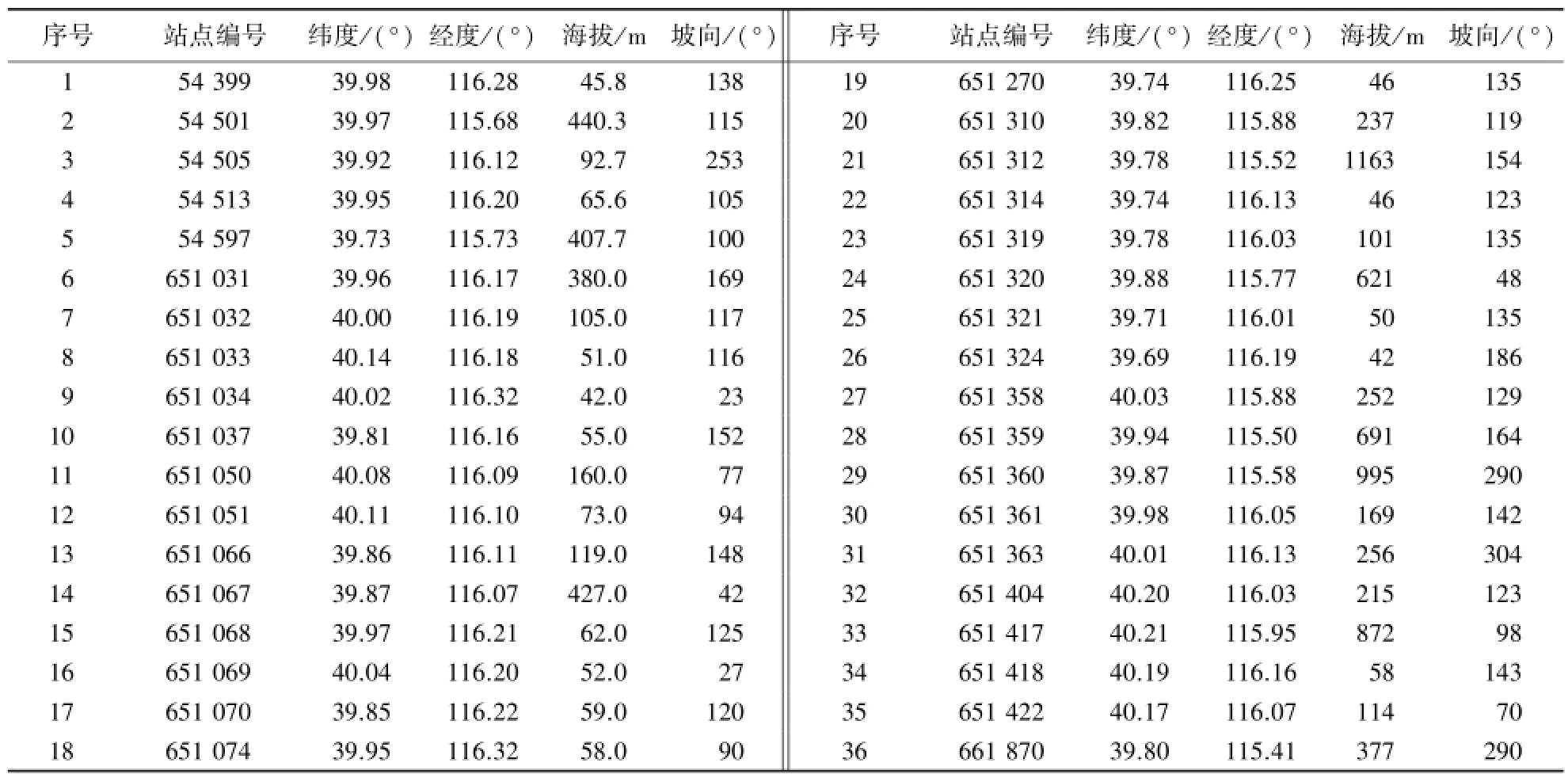
表1 气象站点信息表Table 1 Information on meteorological sites

首先要进行海拔与相对湿度的相关性预分析，这是PRISM模型能够插值的前提条件.分年、月、日3个尺度判断海拔与平均相对湿度是否有存在线性关系.站点年平均相对湿度通过2012年全年观测值计算的平均值得到，站点月平均相对湿度则通过全月观测值计算的平均值得到，站点日平均相对湿度则是通过全天观测值计算的平均值得到.月平均需要逐月的数据，日平均需要系统抽样选取各个月中旬某天的数据.再分时间尺度综合海拔、坡向、空间坐标、平均相对湿度等多种因子信息形成特定结构格式的站点信息输入数据.最后利用数字高程数据提取坡向栅格数据，并与DEM数据一起作为输入数据.

2.2.2 试验区概况 试验区位于北京市西部山区，属于华北典型的山地地形.该区域位于太行山余脉，其内有东灵山、笔架山、百花山、妙峰山、九龙山等多座山头耸立.全区最低海拔为29 m，最高海拔为2 176 m.山区由昌平、石景山、门头沟、丰台、海淀、房山部分区域组成，地理坐标大致为东经115°59′～116°06′，北纬39°54′～39°57′，面积约3 000 km2，约占全市面积的17%.山区属于半湿润地区，是典型的暖温带大陆性季风气候，干湿适中，四季分明.地区年平均气温为12.2～13.9℃，有效积温3 385～4 210℃，无霜期140 d左右，年平均降水量450～600 mm，汛期降水量约占全年的85%，年平均日照时长为1 963～2 695 h，平均日照辐射为112.16～136.48 kJ·cm－2.植被多为次生落叶林及灌丛，有人工针叶林和1 900 m以上的山地草甸.

2.2.3 精度的验证 日、月、年3个时间尺度下插值结果的精度通过站点之间交叉验证的方式来评估.模型插值误差的评价指标有平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE).MAE反映山地湿度插值模型的准确度，RMSE描述模型插值的误差范围，误差指标值越小说明模型的插值结果越精确.同时利用Arcgis 10.0软件的地统计工具和气象站点上的相对湿度数据进行空间插值，得到相同区域上的其他空间插值模型的插值结果；通过Arcgis 10.0交叉检验工具也得到3个精度指标值，并与PRISM方法的精度指标值进行对比.文中选取的对比插值方法有反距离加权法、径向基函数法、泛克里金法和协同普通克里金法.

3 结果与分析

3.1 相对湿度与海拔的相关性

经SPSS软件分析得出:年平均相对湿度与海拔的相关系数为0.71，月平均相对湿度和日平均相对湿度见表2.其中，月平均相对湿度与海拔的相关系数最小值是0.707，日平均相对湿度与海拔的相关系数最小值是0.719.结果表明大气相对湿度与海拔存在较强的线性关系.相对湿度的月垂直变化率和月平均值的时间序列特征如图2所示，两者的季节变化大致呈倒V字形，3月份至11月份二者的变化趋势一致，但11月至翌年2月二者的变化趋势相反.春夏秋三季内随着大气相对湿度的增加相对湿度的垂直变化率也提高，反之，则相对湿度垂直变化率递减.相对湿度的月垂直变化率和月平均值的时间序列分析结果表明，相对湿度越大，相对湿度的变化范围也越大，从而使得相对湿度月变化率升高.

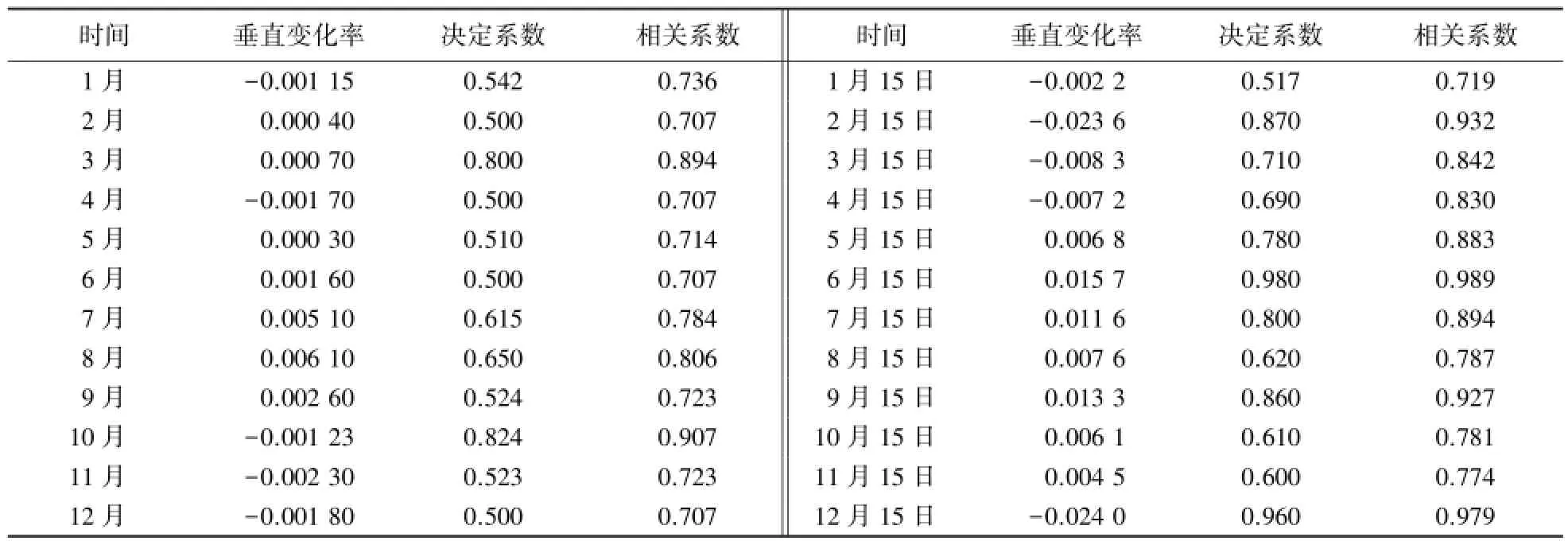
表2 月平均相对湿度与日平均相对湿度的相关系数Table 2 Correlation coefficients of monthly and daily average relative humidity

3.2 插值结果的精度

从整体评估指标和残差结果两方面来评估插值结果的精度.从表3可知:年尺度下平均相对误差在5%以内；月尺度下平均绝对误差的最大值是3.9%，最小值是2.43%，平均相对误差的范围在10%以内，均方根误差为1.8%～4.8%；日尺度下平均绝对误差的最大值是6.21%，最小值是3.07%，平均相对误差在25%以内，均方根误差为1.78%～5.84%.上述MAE、MRE及RMSE指标说明年平均相对湿度预测的误差小于月平均相对湿度的误差，月平均相对湿度预测误差小于日平均相对湿度的误差.综合上述指标，结果表明基于PRISM的插值模型在山地大气湿度插值的应用上基本上达到精度要求，即相对误差在10%之内，而且时间尺度越大模型精度越高.

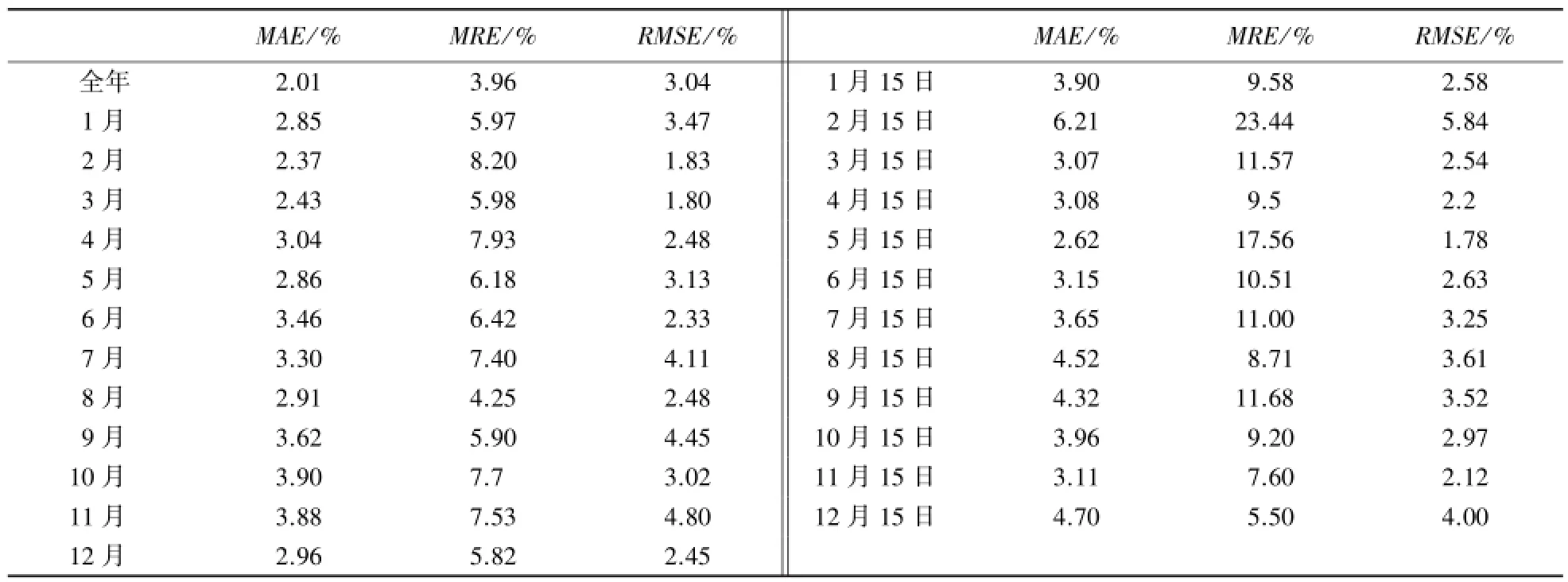
表3 3种时间尺度下平均相对湿度的预测精度Table 3 Accuracy of prediction on average relative humidity in different time scales

从图3可知，残差分布图显示除少数站点外，其他所有站点都在置信区间内且均匀分布在X轴两侧，表明预测残差是正态分布；PRISM插值模型的插值精度高，结果可信.

3.3 PRISM模型与其他插值模型的平均绝对误差指标的对比

图4A是PRISM插值模型与反距离加权、全局多项式等插值方法精度的对比；PRISM模型的MAE在日尺度下下降0.66%～1.23%，月份尺度下下降0.24%～0.52%，年尺度下下降0.36%～0.66%.图4B是PRISM插值模型与加入海拔的协同普通克里金方法精度的对比.PRISM模型在年尺度下MAE下降0.4%，月尺度下MAE下降0.38%，日尺度下MAE下降0.41%.综合上述，基于PRISM原理的山地气象空间插值模型在综合考虑了空间距离、海拔、坡向因素后，插值精度比其他插值方法有较大提高.

3.4 不同时间尺度下的相对湿度空间分布特征

以2012年、2012年8月、2012年7月15日为例子，利用山地大气湿度空间插值模型进行模拟，分别得到年、月、日3个尺度下的相对湿度分布场(图5).

4 讨论

本研究中，山地大气湿度空间插值模型综合考虑了海拔、坡向等地形因子影响山地湿度的气象机理，从而适用于山地大气湿度的空间分布模拟.上述结果与宋亚男等[31]以华北地区为例子对相对湿度空间插值研究的结果一致，即时间尺度越大平均相对湿度的空间插值精度越高.本研究结果也表明基于PRISM的空间插值程序能快速实现对山地大气湿度场的精确模拟，且插值精度优于反距离加权方法、径向基函数方法、泛克里金方法和协同普通克里金方法.

[1]李海涛，沈文清，夏军.MTCLIM模型系列研究报告(2):湿度估算方法在中国亚热带山地的有效性验证[J].山地学报，2003，21(4):395－401.

[2]马剑芳，马钦彦，康峰峰，等.山西太岳山油松林木夏季树干液流速率的研究[J].北京林业大学学报，2005，27(S2):160－164.

[3]高开通，刘鹏举，唐小明.森林资源小班火险天气等级预报方法研究[J].北京林业大学学报，2013，35(4):61－66.

[4]刘学勤，奥小平，何力春.宜林荒山春季土壤含水率与气象因子的相关分析[J].北京林业大学学报，1993，15(3):26－33. [5]林智慧，杨建全，郑敏琳，等.湿度对褐背小萤叶甲生长发育的影响[J].福建农林大学学报(自然科学版)，2004，33(1):42－45.

[6]潘炜，付月生，邢金鹏，等.环境温度对蜂巢内温湿度的影响[J].福建农林大学学报(自然科学版)，2016，45(3):316－319.

[7]王书光，周在敏，栾树杰，等.红松人工林林木直径生长与气象因子的相关分析[J].沈阳农业大学学报，1990，21(3):247－250.

[8]侯光雷.吉林省中部地表温度和湿度的反演及空间分布[D].长春:东北师范大学，2008.

[9]周红艺，叶颖燊，李辉霞.基于DEM的广东省平均气温空间插值Ⅰ:研究方法[J].佛山科学技术学院学报(自然科学版)，2014，32(2):6－9.

[10]张洪亮，倪绍祥，邓自旺，等.基于DEM的山区气温空间模拟方法[J].山地学报.2002，20(3):360－364.

[11]何杰颖，张升伟.地基和星载微波辐射计数据反演大气湿度[J].电波科学学报，2011，26(2):362－368.

[12]李正泉，于贵瑞，刘新安，等.东北地区降水与湿度气候资料的栅格化技术[J].资源科学，2003，25(1):72－77.

[13]刘旸，管莉.人工神经网络法反演晴空大气湿度廓线的研究[J].气象，2011，37(3):318－324.

[14]胡丹桂，舒红.基于协同克里金空气湿度空间插值研究[J].湖北农业科学，2014，53(9):2 046－2 049.

[15]马轩龙，李春娥，陈全功.基于GIS的气象要素空间插值方法研究[J].草业科学，2008，25(11):13－19.

[16]朱华忠，罗天祥，CHRISTOPHER D.中国高分辨率温度和降水模拟数据的验证[J].地理研究，2003，22(3):349－359.

[17]封志明，杨艳昭，丁晓强，等.气象要素空间插值方法优化[J].地理研究，2004，23(3):357－364.

[18]李新，程国栋，卢玲.空间内插方法比较[J].地球科学进展，2000，15(3):260－265.

[19]DALY C，NEILSON R P，PHILLIPS D L.A statistical-topographic model for mapping climatological precipitation over mountain terrain[J].Journal of Applied Meteorology，1994，33:140－158.

[20]GLASSY J M，RUNNING S W.Validating diurnal climatology logic of the MTCLIM model across a climate gradien in Oregon [J].Ecol Appl，1994，4(2):248－679.

[21]KIM J P，KIM G，LEE W S，et al.Estimation of monthly areal precipitation using Daymet and PRISM[J].Journal of Korean Society of Hazard Mitigation，2012，12(5):83－90.

[22]赵登忠，张万昌，刘三超.基于DEM的地理要素PRISM空间内插研究[J].地理科学，2004，24(2):205－211.

[23]夏智武，刘鹏举，陈增威，等.山地环境日气温PRISM空间插值研究[J].北京林业大学学报，2016，38(1):83－90.

[24]韩庆红，陈渭民，王普才，等.PRISM在松花江流域降水分布中的应用研究[J].南京气象学报，2006，29(1):56－61.

[25]朱求安，张万昌，赵登忠.基于PRISM和泰森多边形的地形要素日降水量空间插值研究[J].地理科学，2005，25(2): 233－238.

[26]DALY C，GIBSON W P，TAYLOR G H，et al.A knowledge-based approach to the statistical mapping of climate[J].Climate Research，2002，22(2):99－113.

[27]DALY C，HELMER E H，QUINONES M.Mapping the climate of Puerto Rico，Vieques and Culebra[J].International Journal of Climatology，2003，23(11):59－81.

[28]KINBALL J S，RUNNING S W，NENANI R R.An improved method for estimating surface humidity from daily minimum temperature[J].Agri For Meteorol，1997，85:85－98.

[29]CHRISTOPHER D，MICHAEL H，SMITH J I，et al.Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States[J].International Journal of Climatology，2008，28(15):2 031－2 064.

[30]徐成东.基于线性加权回归模型的降水量空间插值方法研究[D].郑州:河南大学，2008.

[31]宋亚男，王秀兰，冯仲科.区域气象要素的空间插值方法比较研究—以华北地区为例[J].山东林业科技，2014，44(6):1－6.

(责任编辑:叶济蓉)

Spatial interpolation of humidity over mountain area based on PRISM

JIANG Yuhao，LIU Pengju，XIA Zhiwu，JIA Daoxiang，YAN Ming
(Research Institute of Resource Information Techniques，Chinese Academy of Forestry，Beijing 100091，China)

To investigate spatial distribution characteristics of humidity across mountainous area in western Beijing，spatial interpolation model based on parameter-elevation regression on independent slopes model(PRISM)principle was applied to hourly humidity data from 36 stations of Meteorological Science Data Sharing Platform and 1∶250000 DEM data across western mountainous area in Beijing.Then grid information on atmospheric relative humidity under time scales of yearly，monthly and daily was generated.Moreover，accuracy of the model was evaluated by cross validation among the sites and comparison with other models like inverse-distanceweighting，Kriging and polynomial.The result showed that this spatial interpolation model based on PRISM was suitable for simulating atmospheric humidity distribution over mountainous area in northern China.Interpolation accuracies for monthly and annual average relative humidity were greatly improved.And its interpolation accuracy was higher than other interpolation methods which only considered space distance or space distance together with altitude.

atmospheric humidity；spatial interpolation；parameter-elevation regression on independent slopes model；weighted linear least squares regression

S716.2；P456.7

:A

:1671-5470(2016)06-0692-08

10.13323/j.cnki.j.fafu(nat.sci.).2016.06.014

2016－03－11

:2016－06－21

“863”计划资助项目(2012AA102001-2).

蒋育昊(1991－)，男，硕士研究生.研究方向:地理信息系统开发与应用.通讯作者刘鹏举(1973－)，男，副研究员，博士.研究方向:林业GIS应用与开发.Email:liupeng＠caf.ac.cn.