A NOTE ON HOMOGENIZATION OF THE HYPERBOLIC PROBLEMS WITH IMPERFECT INTERFACES

YANG Zhan-ying,YU Yun-xia

(1.School of Mathematics and Statistics,South-Central University for Nationalities, Wuhan 430074,China )

(2.Department of Mathematics,Xinxiang University,Xinxiang 453000,China )

A NOTE ON HOMOGENIZATION OF THE HYPERBOLIC PROBLEMS WITH IMPERFECT INTERFACES

YANG Zhan-ying1,YU Yun-xia2

(1.School of Mathematics and Statistics,South-Central University for Nationalities, Wuhan 430074,China )

(2.Department of Mathematics,Xinxiang University,Xinxiang 453000,China )

In this paper,we are concerned with a class of hyperbolic problems with nonperiodic coefficients in two-component domains.By the periodic unfolding method,we derive the homogenization and corrector results,which generalize those achieved by Donato,Faella and Monsurr.

hyperbolic problems;periodic unfolding method;homogenization;correctors

1 Introduction

In this paper,we study the homogenization and corrector results for the following hyperbolic problem with-1＜γ＜1,

where Ω⊂Rnis the union of two ε-periodic sub-domains Ω1εand Ω2ε,separated by an interface Γε,such that Ω1ε∪2ε=Ω and Γε=∂Ω2ε.Here,Ω1εis connected and the number of connected components of Ω2εis of order ε-n.This problem models the wave propagationin a medium made up of two materials with different coefficients of propagation.For the physical model,we refer the reader to Carslaw and Jaeger[1].

Let Y=[0,l1)×···×[0,ln)be the reference cell with li＞0,i=1,···,n.We suppose that Y1and Y2are two nonempty open disjoint subsets of Y such that Y=Y1∪,where Y1is connected and Γ=∂Y2is Lipschitz continuous.Throughout this paper,we have the following assumptions.

•For any ε,Aε(x)=is a matrix satisfying the following:

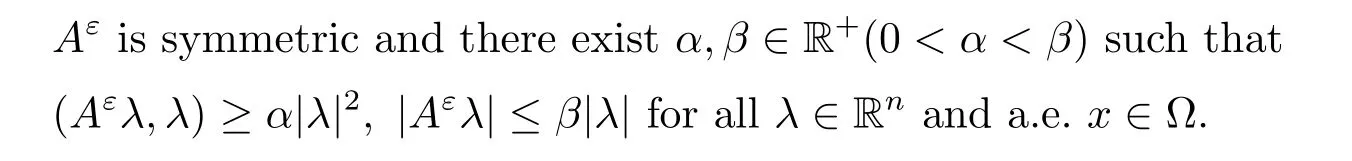
•For any ε,hε(x)=h(x/ε),where h is a Y-periodic function such that h∈L∞(Γ)and there exists h0∈R such that 0＜h0＜h(y)a.e.on Γ.

•The initial data satisfy the assumptions:

For the classical case Aε(x)=A(x/ε)with A being periodic,symmetric,bounded and uniformly elliptic,Donato,Faella and Monsurrgave the homogenization for γ≤1 in[2]. Later,they obtained the corrector results in[3]for-1＜γ≤1.Their proofs are based on the oscillating test functions method.In[4],the first author gave the corrector results for γ＜-1 by the unfolding method.However,the above methods do not work for the case that Aε(x)is non-periodic coefficient matrix.

In this paper,we will consider problem(1.1)with Aε(x)being non-periodic for-1＜γ＜1.More precisely,suppose that there exists a matrix A=(aij)1≤i,j≤nsuch that

where Tεis the unfolding operator.By the unfolding method,we derive the homogenization and corrector results for-1＜γ＜1.Next,we state our main theorems,in which we will use some notations to be defined in the next section.We first state the homogenization results whose unfolded formulation will be provided for the study of correctors in Section 3.

Theorem 1.1For-1＜γ＜1,let uεbe the solution of problem(1.1)with(1.2).We further suppose that

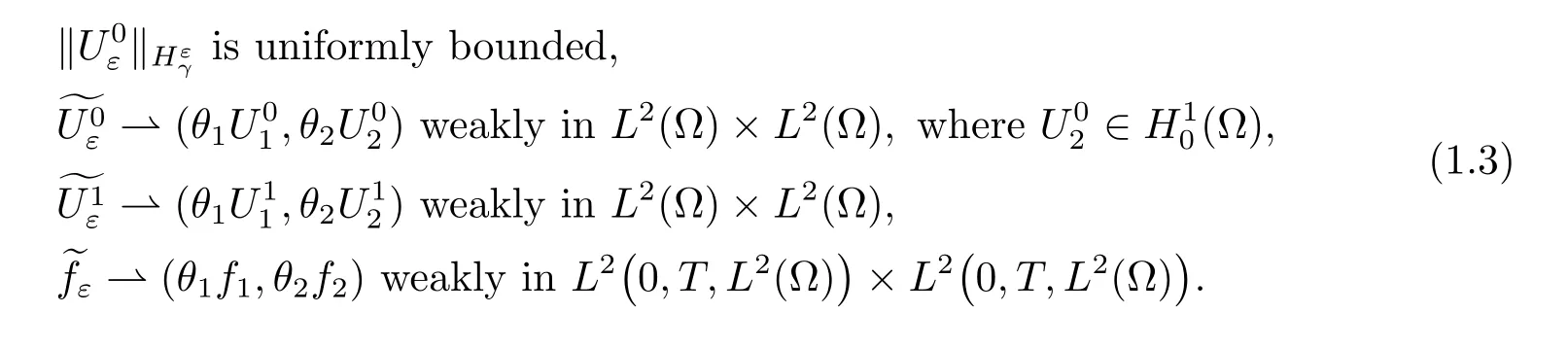
Then there exists u1∈L∞such that

Also,u1is the unique solution of the following problem:

where the homogenized matrix A0=is defined by

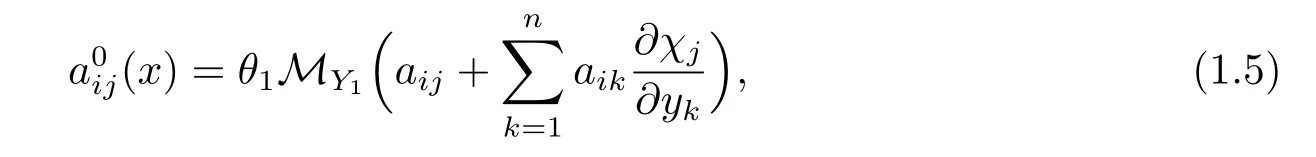
and χj∈L∞(Ω;(Y1))(j=1,···,n)is the solution of the following cell problem:

Further,we have the following precise convergence of flux:

Notice that the homogenized matrix A0still depends on x,compared with the classical constant matrix(see for instance[2,4]).

In order to investigate the corrector results,we need stronger assumptions on the initial data than that of the convergence results,as already evidenced in the classical works(see, for instance,[3,5]).Here we impose some assumptions,introduced by the first author(see [4]for more details),which are slightly weaker than those in[3].Now we list them as follows.

(i)For fiε∈L2

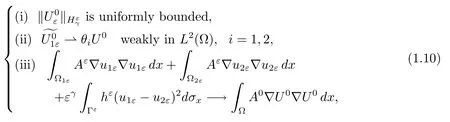
where U0is given in

These assumptions ensure the convergence of the energy in C0([0,T]).Moreover,we obtain the following corrector results.

Theorem 1.2For-1＜γ＜1,let uεbe the solution of problem(1.1)with(1.2). Suppose that the initial data satisfy(1.8)–(1.10).Let u1be the solution of the homogenized problem(1.4),then we have the following corrector results:

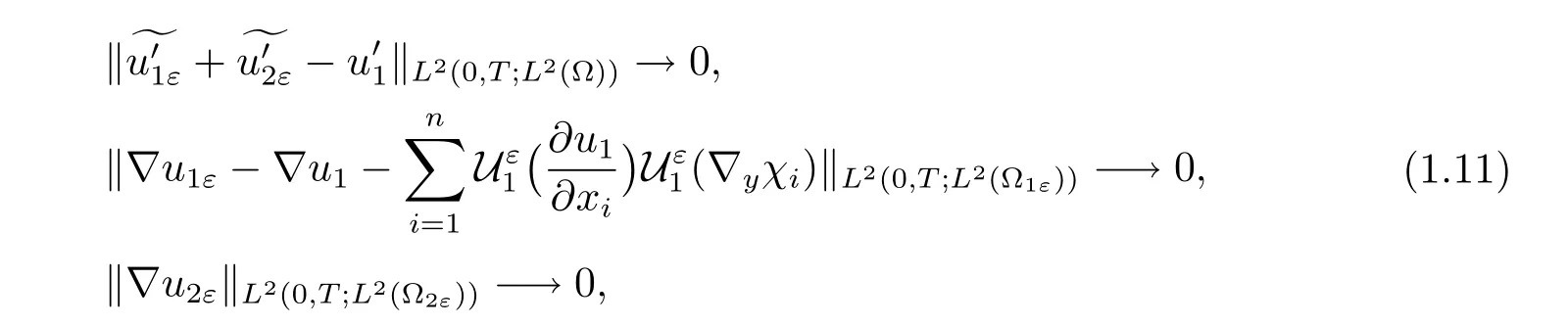
where χj∈L∞is the solution of the cell problem(1.6).

For the parabolic case,Jose[6]proved the homogenization for γ≤1.Later,the corrector results for-1＜γ≤1 were given by Donato and Jose[7].Recently,by the unfolding method,the first author obtained the homogenization and corrector results for γ≤1 in[8].Our results are also related to those of hyperbolic problems in perforated domains which were studied in[9,10].

The paper is organized as follows.In Section 2,we briefly recall the unfolding method in perforated domains.Section 3 is devoted to the homogenization result.In Section 4,we prove the corrector results.

2 Preliminaries

Let Ω⊂Rnbe an open and bounded set with Lipschitz continuous boundary.Let ε be the general term of a sequence of positive real numbers which converges to zero.

For any k∈Zn,we denote

where kl=(k1l1,···,knln)and i=1,2.For any fixed ε,let Kε=1,2}.We suppose that

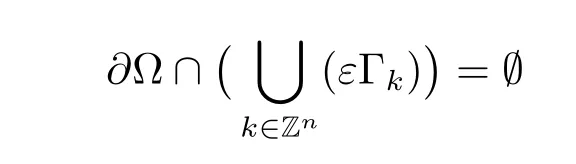
and define the two components of Ω and the interface respectively by

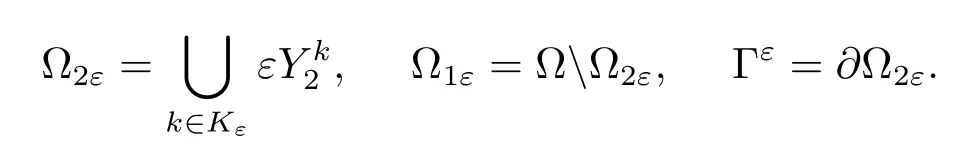
Observe that∂Ω and Γεare disjoint,the component Ω1εis connected and the componentΩ2εis union of ε-ndisjoint translated sets of εY2.

The following notations are related to the unfolding method in[11–13]:

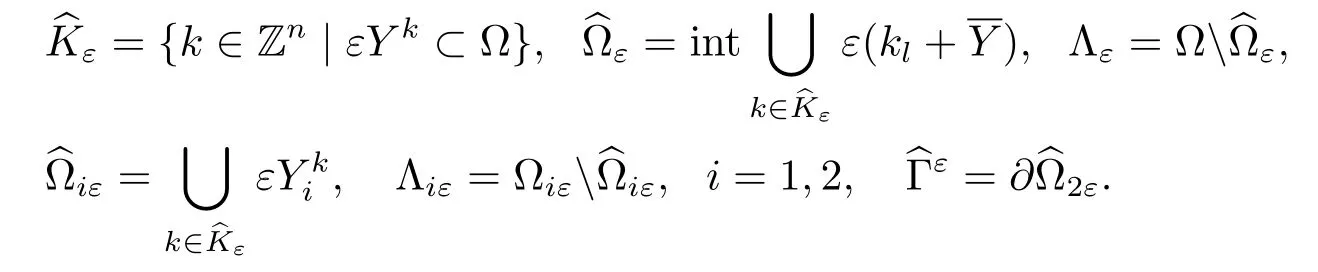
This paper will also use the following notations:

•θi=

•MO(v)=

•Vεis defined by

endowed with the norm‖v‖Vε=‖∇v‖L2(Ω1ε).

•For any γ∈R,the product space

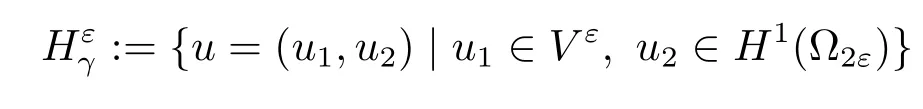
is equipped with the norm

•C denotes generic constant which does not depend upon ε.

•The notation Lp(O)will be used both for scalar and vector-valued functions defined on the set O,since no ambiguity will arise.

In the rest of this section,we give a brief review of the unfolding operators in twocomponent domains.We refer the reader to[9]and[14]for further properties and related comments.

For any x∈Rn,we use[x]Yto denote its integer part(k1l1,···,knln)such that x-[x]Y∈Y,and set{x}Y=x-[x]Y.Then one has

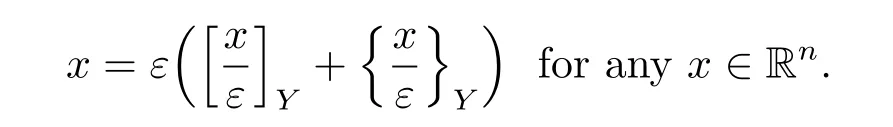
Definition 2.1[2]Let i=1,2.For p∈[1,+∞)and q∈[1,∞],let φ∈Lq(0,T;Lp(Ωiε)). The unfolding operatoris defined as follows:

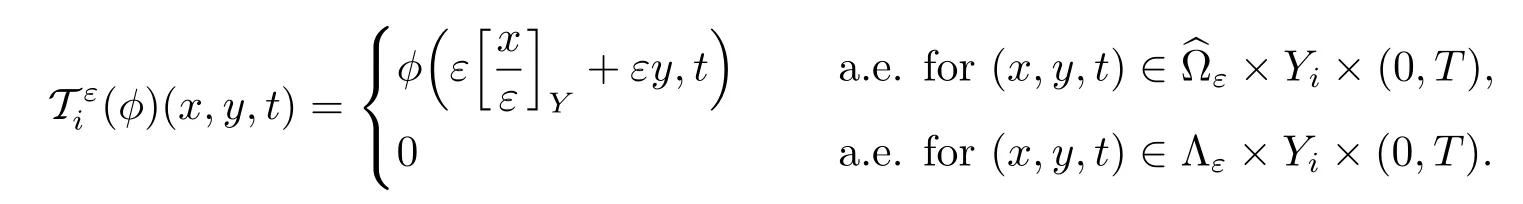
Definition 2.2[2]Let i=1,2.For p∈[1,+∞)and q∈[1,+∞],let φ be in Lq(0,T;Lp(Ω×Yi)).The averaging operatoris defined as follows:

Proposition 2.3For p∈[1,+∞)and q∈[1,∞],let φ∈Lq(0,T;L1(Ωiε)).Then for a.e.t∈(0,T),we have

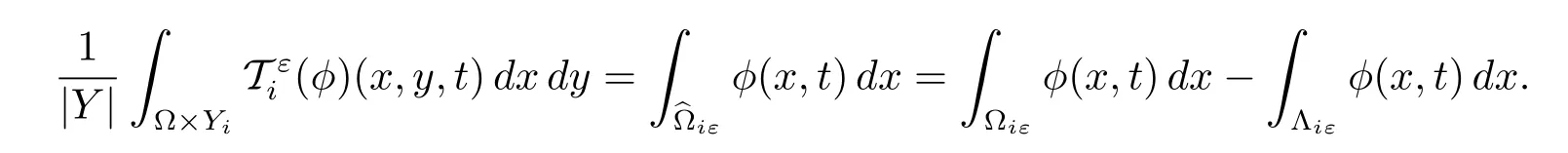
Proposition 2.4(some convergence properties)

(i)Let ω∈L2

(ii)Let ωε∈L2(0,T;L2(Ωiε))and ω∈L2(0,T;L2(Ω)),then the following two assertions are equivalent:

(iii)Let ωε∈L2(0,T;L2(Ωiε))and ω∈L2(0,T;L2(Ω×Yi)),then the following two assertions are equivalent:

Following the arguments in the proof of[Proposition 1.7,14](see also[Proposition 2.13, 9]),we can obtain the following result which will be used to get the corrector results.

Proposition 2.5Let p,q∈[1,∞),for i=1,2,let f∈Lq(0,T;Lp(Ω))and g∈L∞(Ω;Lp(Yi)),then we have

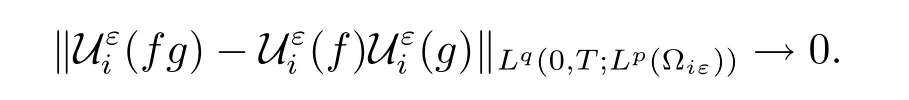
We end this subsection with the following convergence theorem which is crucial to obtaining our homogenization result.

Theorem 2.6Let uε=(u1ε,u2ε)and{uε}be in L∞(0,T;)with-1＜γ＜1.If

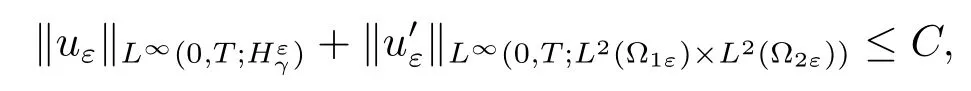
then there exist u1∈L∞for a.e.x∈Ω,such that,up to a subsequence(still denoted by ε),

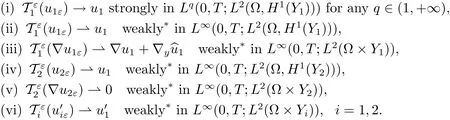
In fact,the proof can be obtained by following the lines of the proofs of[Theorem 2.12, 14](see also[Theorem 2.19,9])and[Theorem 2.20,13].

3 Homogenization Results

In this section,we are devoted to the asymptotic behavior of the hyperbolic problem (1.1).For every fixed ε,the Galerkin method provides that problem(1.1)has a unique solution uε.Under assumption(1.3),following the arguments in[2],we can obtain the following uniform estimate,

Now,we state the unfolded formulation of the homogenization results(see Theorem 1.1)which will be used for getting the corrector results.

Theorem 3.1Under the assumptions of Theorem 1.1,there exist u1∈L∞(0,T;(Ω))=0 such that

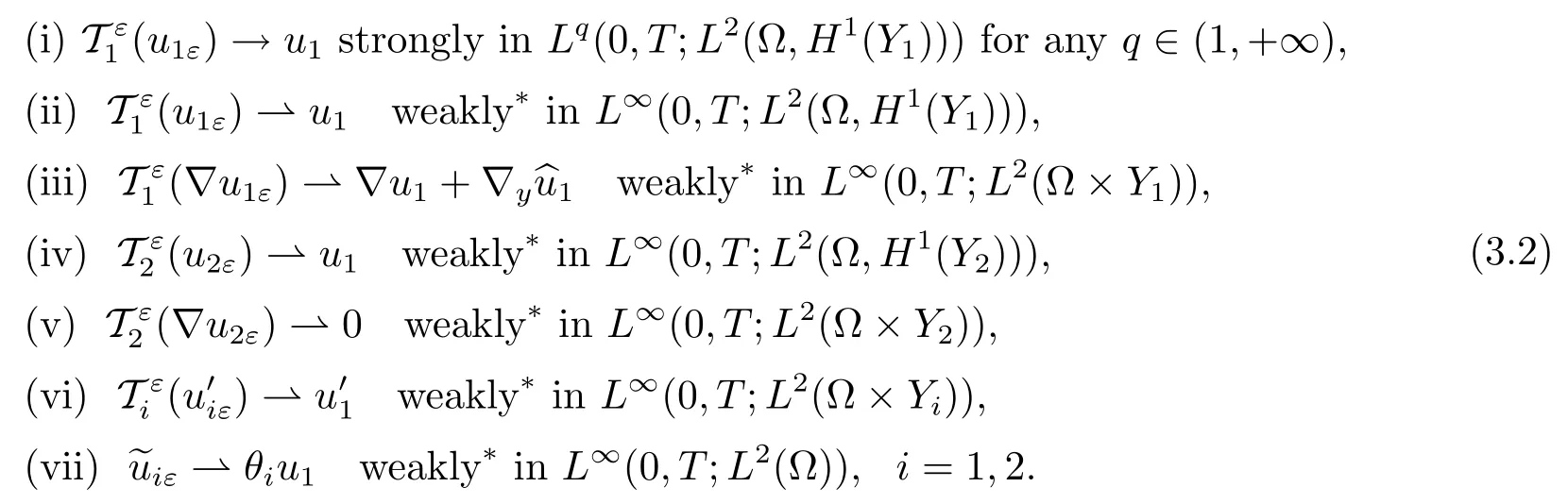
where χj∈L∞(Ω;(Y))(j=1,···,n)is the solution of the cell problem(1.6).

The proofs of Theorem 3.1 and Theorem 1.1 mainly rely on the periodic unfolding method.Indeed,following the lines of proof of Theorem 3.1[4],we can use Theorem 2.6 to obtain the proofs of these two theorems.

Remark 3.2Following the framework in the proof of Theorem 3.2[8],we derive

which will be used in the proof of Corollary 4.2.

Remark 3.3In Theorem 1.1,we exclude the case γ=1.For this case,the homogenized problem is a coupled system of a PDE and an ODE.As a result,the corrector results are more complicated.

4 Proof of Theorem 1.2

In this section,we are devoted to the proof of corrector results.To do that,we need some stronger assumptions than those of the homogenization results.Here,we impose the assumptions(1.8)–(1.10),as presented in[4],which are slightly weaker than those in[3]. Under these assumptions,the energy of problem(1.1)converges in C0([0,T])to that of the homogenized one.Moreover,we obtain that some convergences in(3.2)are strong ones.

For each ε,the energy Eε(t),associated to the problem(1.1),is defined by

The energy associated to the homogenized problem(1.4)is defined by

Following the classical arguments(see for instance[3]),we have the following result.

Theorem 4.1Let γ∈(-1,1).Suppose that uεis the solution of problem(1.1)with the initial data satisfying(1.8)–(1.10).Let u1be the solution of the homogenized problem (1.4),then we have

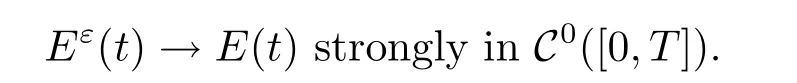
Corollary 4.2Under the assumptions of Theorem 4.1,we have

To prove this corollary,we need the following classical result.

Proposition 4.3(see[14])Let{Dε}be a sequence of n×n matrices in M(α,β,O) for some open set O,such that Dε→D a.e.on O(or more generally,in measure in O).If ζε⇀ζ weakly in L2(O),then

Proof of Corollary 4.2From(3.4),we have

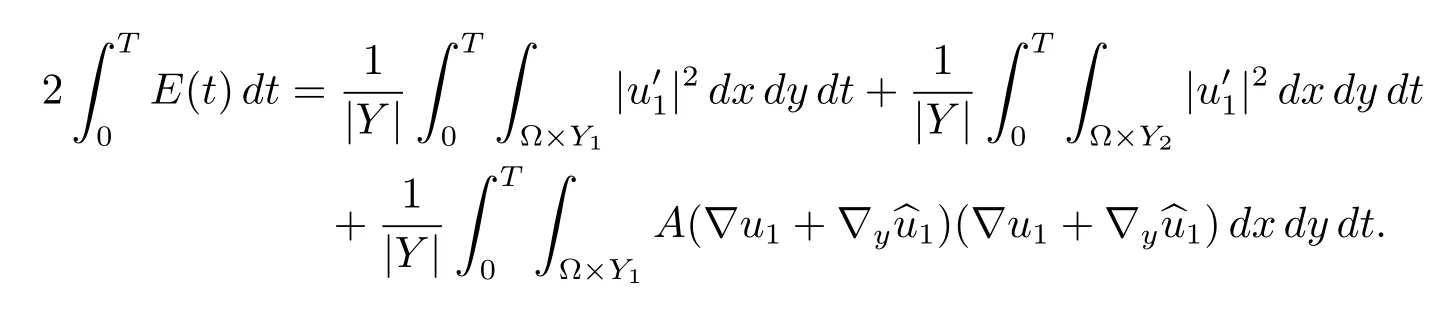
By Proposition 4.3 and the weak lower-semicontinuity,we deduce

Thus,Proposition 2.3 allows us to get that

The former equality implies that

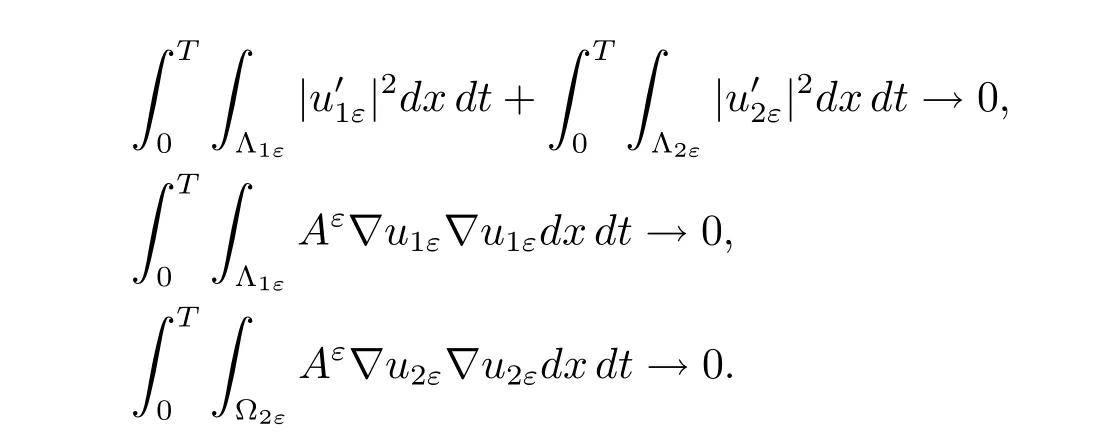
These give the first line and(iii)in(4.1)due to the ellipticity of Aε.

By the latter equality in(4.2)and Proposition 2.3,we know

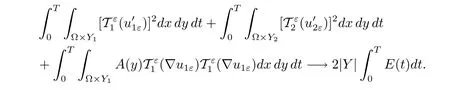
Combining this with(3.2),we obtain

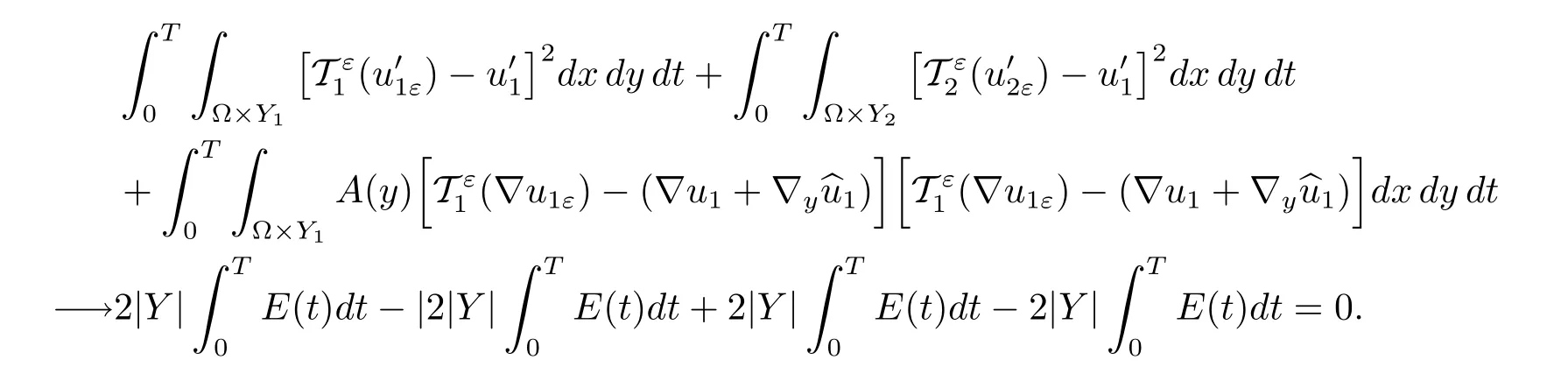
This together with the ellipticity of A,allows us to obtain the rest convergences in(4.1).

Proof of Theorem 1.2Observe that u1is independent of y.By(ii)of Proposition 2.4, the first convergence in(1.11)follows from(i)in Corollary 4.2.By(i)and(ii)in Corollary 4.2,we use(iii)of Proposition 2.4 to get

By the fact that∇u1is independent of y,(i)of Proposition 2.4 gives

Together with(3.3)and Proposition 2.5,we complete the proof of Theorem 1.2.

[1]Carslaw H S,Jaeger J C.Conduction of heat in solids[M].Oxford:Clarendon Press,1947.

[2]Donato P,Faella L,MonsurrS.Homogenization of the wave equation in composites with imperfect interface:A memory effect[J].J.Math.Pures Appl.,2007,87(2):119–143.

[3]Donato P,Faella L,MonsurrS.Correctors for the homogenization of a class of hyperbolic equations with imperfect interfaces[J].SIAM J.Math.Anal.,2009,40(5):1952–1978.

[4]Yang Zhanying.Homogenization and correctors for the hyperbolic problems with imperfect interfaces via the periodic unfolding method[J].Commu.Pure Appl.Anal.,2014,13(1):249–272.

[5]Cioranescu D,Donato P.An Introduction to Homogenization[M].Oxford:Oxford Univ.Press,1999.

[6]Jose E C.Homogenization of a parabolic problem with an imperfect interface[J].Rev.Rouma.Math. Pures Appl.,2009,54(3):189–222.

[7]Donato P,Jose E C.Corrector results for a parabolic problem with a memory effect[J].ESAIM: Math.Model.Num.Anal.,2010,44(3):421–454.

[8]Yang Zhanying.The periodic unfolding method for a class of parabolic problems with imperfect interfaces[J].ESAIM:Math.Model.Num.Anal.,2014,48(5):1279–1302.

[9]Donato P,Yang Zhanying.The periodic unfolding method for the wave equation in domains with holes[J].Adv.Math.Sci.Appl.,2012,22(2):521–551.

[10]Nabil A.A corrector result for the wave equations in perforated domains[J].GAKUTO Internat. Ser.Math.Sci.Appl.,1997,9:309–321.

[11]Cioranescu D,Damlamian A,Griso G.Periodic unfolding and homogenization[J].C.R.Math.Acad. Sci.Paris,2002,335(1):99–104.

[12]Cioranescu D,Damlamian A,Griso G.The periodic unfolding method in homogenization[J].SIAM J.Math.Anal.,2008,40(4):1585–1620.

[13]Donato P,Le Nguyen K H,Tardieu R.The periodic unfolding method for a class of imperfect transmission problems[J].J.Math.Sci.,2011,176(6):891–927.

[14]Cioranescu D,Damlamian A,Donato P,Griso G,Zaki R.The periodic unfolding method in domains with holes[J].SIAM J.Math.Anal.,2012,44(2):718–760.

[15]Chen Jiajia,Mu Chunlai.The upper and lower bound on the blow-up phenomena for some nonlinear parabolic systems[J].J.Math.,2012,32(5):897–903.

带不完美界面的双曲问题均匀化的一个注记

杨占英1,于云霞2

(1.中南民族大学数学与统计学学院,湖北武汉430074)

(2.新乡学院数学系,河南新乡453000)

本文研究了一类二分区域上的具有非周期系数的双曲问题.利用周期Unfolding方法,得到了均匀化及其矫正结果,推广了Donato,Faella和Monsurr的工作.

双曲问题;周期Unfolding方法;均匀化;矫正

O175.23;O175.27

tion:35B27;35L20

A

0255-7797(2017)01-0028-11

∗Received date:2015-06-05Accepted date:2015-09-09

Foundation item:Supported by National Natural Science Foundation of China(11401595).

Biography:Yang Zhanying(1980–),female,born at Zhoukou,Henan,associate professor,major in homogenization theory and its application.