A MASCHKE TYPE THEOREM FOR PARTIAL π-COMODULES

JIA Ling,CHEN Xiao-yuan

(1.Department of Mathematics and Statistics,Ludong University,Yantai 264025,China )

(2.Basic Department,Zhejiang Business College,Hangzhou 310053,China )

A MASCHKE TYPE THEOREM FOR PARTIAL π-COMODULES

JIA Ling1,CHEN Xiao-yuan2

(1.Department of Mathematics and Statistics,Ludong University,Yantai 264025,China )

(2.Basic Department,Zhejiang Business College,Hangzhou 310053,China )

In this paper,we study the Maschke type theorems of partial group comodules. By the methods of weak Hopf group coalgebras,we obtain the classical Maschke type theorems of Hopf algebras,which generalized those of Hopf algebras and results of[8].

partial π-comodule;trace map;Maschke type theorem

1 Introduction

Partial actions of groups as powerful tools were introduced during the study of operator algebras by Exel[2].With the further development,many positive results were proposed [3–6].Caenepeel and the other authors developed a theory of partial actions of Hopf algebras [1]and introduced the notion of a partial entwining structure as a generalization of entwining structure(see[9]).

On other hand,the notion of a Hopf π-coalgebra which generalized that of a Hopf algebra was introduced and played an important role,consequently group entwining structures and group weak entwining structure were carefully studied.Motivated by this fact,we introduce the notion of a partial group comodule and give a Maschke type theorem for them.Because the“coassociativity”of a partial structure is destroyed,the generalization is not trivial and easy.

In this paper,we first recall basic definitions of partial group comodules and give some examples.Then we state a Maschke-type theorem of partial group Hopf modules which generalizes the relevant results of Hopf modules(see[7,8]),entwined modules,group Hopf modules,etc..

The organization of the paper is as follows:First we introduce the notion of partial group comodules and then give our main result-Maschke type theorem.

ConventionsWe work over a commutative ring k.We denote by i the unit of the group π and use the standard(co)algebra notation,i.e.,Δ is a coproduct,ε is a counit,m is a product and 1 is a unit.If 1 appears more than once in the same expression,then we use different 1′.The identity map from any k-space V to itself is denoted by idV.Write aαfor any element in Aαand[a]for an element in=A/kerf,where f is a k-linear map. For a right π-C-comodule M,we write ρα,β(m)=for any α,β∈π and m∈Mαβ.

2 The Main Results

Definition 2.1A π-coalgebra over k is a family of C={Cα}α∈πof k-spaces endowed with a family k-linear maps Δ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈πand a k-linear map ε:Ci→k such that for any α,β,γ∈π,

(1)(Δα,β⊗idCγ)Δαβ,γ=(idCα⊗Δβ,γ)Δα,βγ.

(2)(idCα⊗ε)Δα,i=(ε⊗idCα)Δi,α=idCα.

Here we extend the Sweedler notation for comultiplication,we write

Remark(Ci,Δi,i,ε)is a coalgebra in the usual sense.

Definition 2.2A Hopf π-coalgebra(Hopf group coalgebra)is a family of algebras H={Hα}α∈πand also a π-coalgebra{Hα,Δ={Δα,β},ε}α,β∈πendowed with a family S={Sα-1:Hα→Hα-1}α∈πof k-linear maps called an antipode such that for any α∈π.

Definition 2.3Let H be a Hopf group coalgebra and A={Aα}α∈πbe a family of algebras endowed with a family of k-linear maps{ρα,β:Aαβ→Aα⊗Aβ}α,β∈π.A is called a right partial group comodule-algebra if the following conditions are satisfied:

Example 1Let H ba a Hopf group coalgebra and e={eα}α∈πbe a central idempotent such that Δα,β(eαβ)(eα⊗1β)=eα⊗eβand ε(ei)=1,then H is a right partial group comodule-algebra.

Definition 2.4Let H ba a Hopf group coalgebra and A be a right partial group comodule-algebra.An A-module M={Mα}α∈πwith a family of k-linear maps

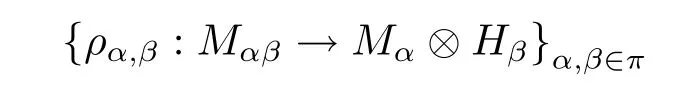
is called a partial(H,A)-Hopf module if the following conditions are verified for any m∈Mα,m′∈Mαβγ,m′′∈Mαβ,a∈Aαβ:

We define the coinvariants of M as

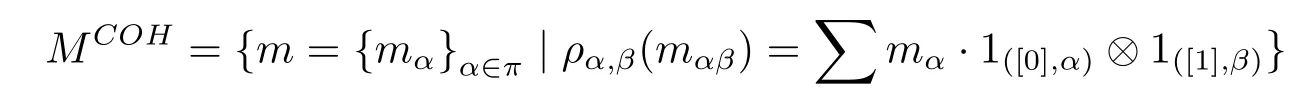
Example 2Let H ba a Hopf group coalgebra and A be a right partial group comodulealgebra.It is easy to prove that A is a partial(H,A)-Hopf module with the multiplications as A-actions.

Definition 2.5Let H ba a Hopf group coalgebra and A be a right partial group comodule-algebra.A right partial π-H-comodule map θ={θα:Hα→Aα}α∈πsuch that=1αis called a right total integral of A.

Definition 2.6Letand tr={trα:Mi→Mα}α∈πbe a family of k-linear maps such that trα(m)=Then tr is called a trace map of M.

In the following parts we always suppose that

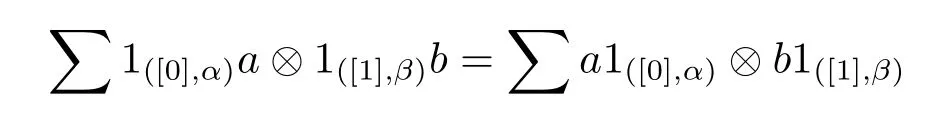
for any a∈Aαand b∈Hβ.

Proposition 2.7m=(mα)α∈πis a coinvariant of M if and only if(m)=m.

ProofIf m=(mα)α∈π∈MCOH,then

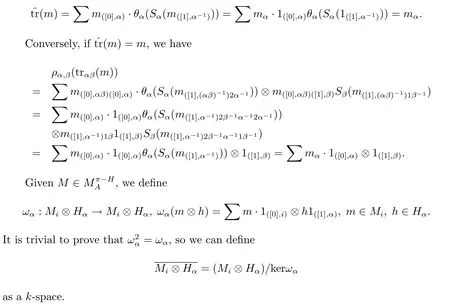
and the partial coactions given by

It is easy to prove that the actions are well-defined.We only have to show the coactions are well-defined.In fact,we have

Then we claim that ξαis well-defined for any α∈π.Indeed,for any m∈Mi,h∈Hα,

Lemma 2.8For any α∈π,canonical map.

ProofIn fact,for any m∈Mα,we have

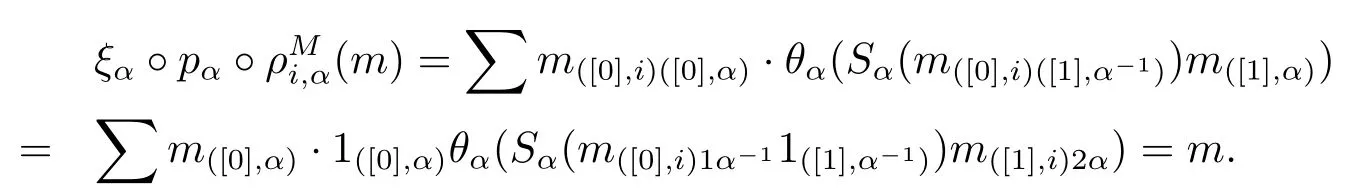
Lemma 2.9If for any α∈π,h∈Hα,a∈Aα,

then ξαis a right Aα-linear map.

ProofIndeed for any α∈π,h∈Hα,a∈Aα,we have

Lemma 2.10Let H ba a Hopf group coalgebra and A be a right partial group comodulealgebra.If the condition in Lemma 2.9 is satisfied,then

ProofIt is sufficed to prove that ξ is right partial π-H-colinear.In fact,for any α,β∈π,h∈Hαβ,m∈Mi,on one hand,Therefore we complete the proof.Now we can give our main result.

Theorem 2.11Let H ba a Hopf group coalgebra and A be a right partial group comodule-algebra with a total integral θ,and M,N∈.Supposing the condition in Lemma 2.9 is satisfied,if fi:Mi→Nisplits as Ai-module map,then f={fα:Mα→Nα}α∈πsplits as partial π-H-comodule map.

ProofAssume that there exits an Ai-module map gi:Ni→Misuch that gifi=idMi. We define

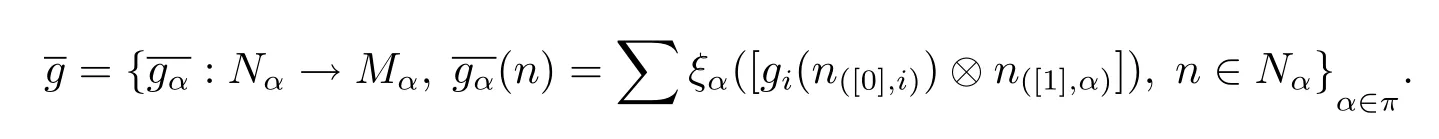
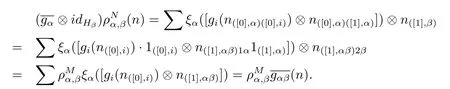
Hence we complete the proof.

[1]Caenepeel S,Janssen K.Partial(co)actions of hopf algebras and partial Hopf-Galois theory[J]. Comm.Algebra,2008,36(8):2923–2946.

[2]Dokuchaev M,Exel R,Piccione P.Partia representations and partial group algebras[J].J.Algebra, 2000,226:251–268.

[3]Dokuchaev M,Exel R.Associativity of crossed products by partial actions enveloping actions and partial representations[J].Trans.Amer.Math.Soc.,2005,357:1931–1952.

[4]Dokuchaev M,Ferrero M,Pacques A.Partial galois theory of commutative rings[J].J.Pure.Appl. Algebra,to appear.

[5]Dokuchaev M,Zhukavets N.On finite degree partial representations of group[J].J.Algebra,2004, 274:309–334.

[6]Exel R.Twisted partial actions:a classification of regular C∗-algebra bundels[J].Proc.London Math.Soc.,1997,74:417–443.

[7]Doi Y.Hopf Extensions of algebras and maschke type theorems[J].Israel J.Math.,1990,72(1-2): 99–108.

[8]Jia Ling.A Maschke-type theorem for a partial entwining structure[J].Taiwanese J.Math.,2010, 14(4):1571–1576.

[9]Guo Jingjing,Zhao Wenzheng.Relative Hopf modules and generalized cleft extensions[J].J.Math., 2011,31(3):21–29.

偏π-余模的Maschke型定理

贾玲1,陈笑缘2

(1.鲁东大学数学与统计科学学院,山东烟台264025)

(2.浙江商业职业技术学院基础部,浙江杭州310053)

本文研究了偏群余模的Mashcke型定理.利用弱Hopf群余代数推广Hopf代数的方法,获得了偏群余模的Mashcke型定理.推广了Hopf代数理论中的Maschke型定理和[8]的相关结论.

偏群余模;迹映射;Maschke型定理

O153.3

tion:16W30

A

0255-7797(2017)01-0021-07

∗Received date:2014-09-05Accepted date:2015-05-06

Foundationitem:SupportedbyNaturalScienceFoundationofShandongProvience (ZR2012AL02).

Biography:Jia Ling(1974–),female,born at Ji’nan,Shandong,associate professor,major in Hopf algebra.