INTERCHANGE BETWEEN WEAK ORLICE-HARDY SPACES WITH CONCAVE FUNCTIONS THROUGH MARTINGALE TRANSFORMS

GUO Hong-ping,YU Lin,JIANG Qin

(1.Department of Mathematics and Finance,Hanjiang Normal University,Shiyan 442000,China )

(2.School of Science,China Three Gorges University,Yichang 443002,China )

(3.Department of Computer Science,Hanjiang Normal University,Shiyan 442000,China )

INTERCHANGE BETWEEN WEAK ORLICE-HARDY SPACES WITH CONCAVE FUNCTIONS THROUGH MARTINGALE TRANSFORMS

GUO Hong-ping1,YU Lin2,JIANG Qin3

(1.Department of Mathematics and Finance,Hanjiang Normal University,Shiyan 442000,China )

(2.School of Science,China Three Gorges University,Yichang 443002,China )

(3.Department of Computer Science,Hanjiang Normal University,Shiyan 442000,China )

In this paper,we consider the interchanging relation between two weak Orlicz-Hardy spaces associated concave functions of martingales.By the means of martingale transform, we prove the result that the elements in weak Orlicz-Hardy space wHΦ1are none other than the martingale transforms of those in wHΦ2,where Φ1is a concave Young function,Φ2is a concave or a convex Young function and Φ1Φ2in some sense.It extends the corresponding results in the literature from strong-type spaces to the setting of weak-type spaces,from norm inequalities to quasi-norm inequalities as well.

martingale transform;weak Orlicz-Hardy space;concave function

1 Introduction

In this paper,we extend some classical results of martingale transforms from the strongtype spaces(normed space)to the setting of weak-type spaces(quasi-normed space).More precisely,we are interested in the characterization about the interchanging between weak Orlicz-Hardy space wHΦ1and wHΦ2in terms of Burkholder’s martingale transforms.

The first motivation in this paper comes from the classical results of Chao and Long [2],as well as the similar results of Garsia[3]and Weisz[10].The concept of martingale transforms was first introduced by Burkholder[1].It is shown that the martingale transforms are especially useful to study the relations between the“predictable”Hardy spaces of martingales,such as Hp,which is associated with the conditional quadratic variation of martingales.The“characterization”of such spaces via martingale transforms were provided in[2]:the elements in the space Hp1are none other than the martingale transforms of thosein Hp2for 0＜p1＜p2＜∞.All of those results can be found also in the monographs of Long[7]and Weisz[11].

Generally,the similar conclusions were obtained also in the case of Orlicz-Hardy spaces for martingales by Ishak and Mogyordi[4],Meng and Yu[8]and Yu[14–15],according to different situations,respectively.

On the other hand,we also note that in recent years,the weak spaces,including their applications to harmonic analysis and martingale theory,have been got more and more attention.See for example Jiao[5],Nakai[9],Weisz[12–13].Particularly,Liu,Hou and Wang [6]firstly introduced the weak Orlicz-Hardy spaces of martingales and discussed its basic properties and some martingale inequalities.Jiao[5]investigated the embedding relations between weak Orlicz martingale spaces.

This article will focus its attention on the relationship between the weak Orlicz-Hardy spaces wHΦ1and wHΦ2,where Φ1and Φ2are two generalized Young functions(not need to be convex)and Φ1Φ2in some sense(see Definition 2.1).It will be shown that the elements in weak Orlicz-Hardy space wHΦ1are none other than the martingale transforms of those in wHΦ2,which extend the corresponding results in Chao and Long[2]from strongtype spaces to the setting of weak-type spaces.In this paper,we are interested in the case Φ1is not convex.

2 Notations and Lemmas

Let(Ω,F,P)be a probability measure space,let(Fn,n∈N)be a sequence of nondecreasing sub-σ-algebras of F such that F=WFn,and let f=(fn,n∈N)be a martingale adapted to(Fn,n∈N).Denote by df=(dfn,n∈N)the sequence of martingale differences with dfn=fn-fn-1,n≥1,and set f0≡0,F0={∅,Ω}.The conditional quadratic variation of a martingale f is defined by

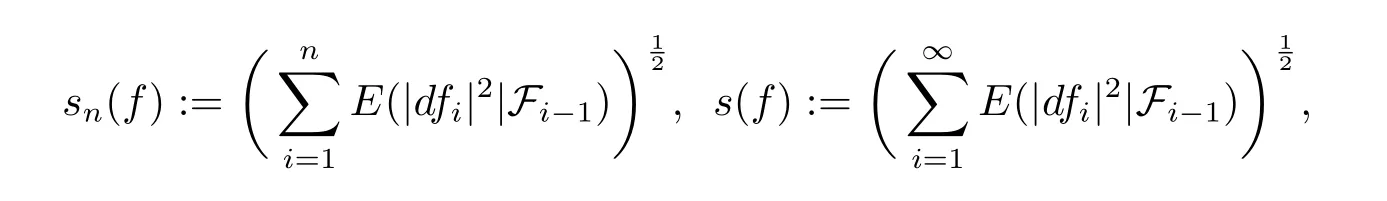
Then for 0＜p≤∞,we define martingale Hardy space as below

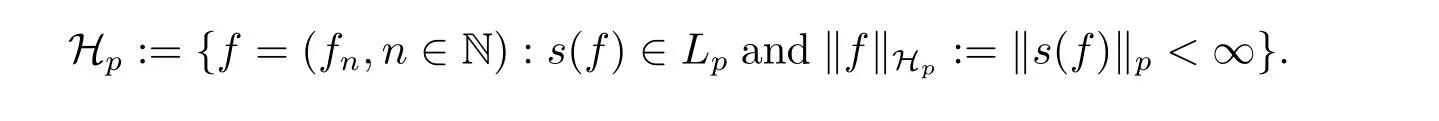
A non-decreasing function Φ(x)is called a generalized Young function(convex or concave),if Φ(x)=φ(t)dt,x≥0,where φ(x)is a left-continuous,non-negative function on[0,+∞). When Φ(x)is a convex Young function,we can define the inverse of φ(t)by ψ(s):=inf{t: φ(t)≥s}.It is well known that its integral Ψ(x)=ψ(t)dt is a convex function and Ψ(x) is called the Young’s complementary function of Φ.The upper index and lower index are defined by

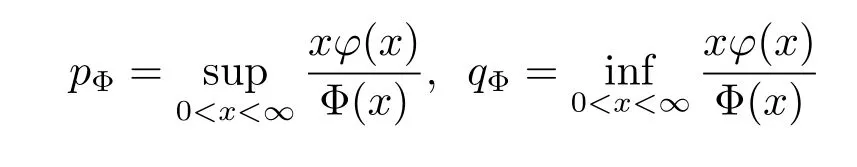
If pΦ＜+∞,then the inverse function Φ-1of Φ exists and has the form

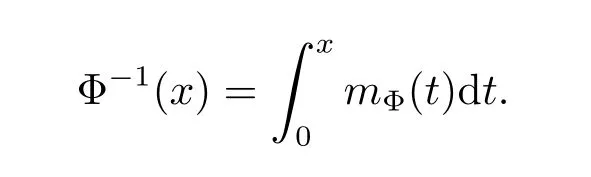
If Φ is convex then mΦ(t)is a decreasing function and we can easily see that(see Ishak and Mogyordi[4])

A function Φ(x)is said to satisfy the Δ2condition(denote Φ∈Δ2)if there is a constant C such that Φ(2t)≤CΦ(t)for all t＞0.It is well known that if Φ(x)is a convex function with pΦ＜+∞then Φ∈Δ2and if Φ(x)is a concave function with qΦ＞0 then Φ∈Δ2.

Let Φ(x)be a generalized Young function.We say that the random variable f belongs to the weak Orlicz space wLΦ=wLΦ(Ω,F,P)if there exists an c＞0 such thatt)＜+∞for all t＞0.In this case we put

The class wLΦis said to be a weak Orlicz space.Some basic facts on weak Orlicz spaces were discussed in Liu,Hou and Wang[6].For example,‖·‖wLΦis a quasi-norm,wLΦis a quasi-Banach space,and LΦwLΦ.If‖f‖wLΦ＜+∞,then

We define the weak Orlicz-Hardy spaces of martingales as below

A new type of partial ordering between pairs of Young functions was introduced by [14–15]as below.

Definition 2.1[14–15]Let Φ1,Φ2be two generalized Young functions.We call that Φ2is more convex than Φ1,Φ2Φ1or Φ1Φ2in symbols,if the compositiona convex function.

Lemma 2.1(see[16])Let Φ1Φ2be two generalized Young functions having lower index qΦ1＞0 and upper index pΦ2＜∞.Then qΦ1,2＞0 and pΦ1,2＜∞.More exactly,we have that

Remark 2.1Since Φ1,2(x)is a convex Young function,we denote by φ1,2(x)and ψ1,2(x) the density functions such that Φ1,2(x)=φ1,2(t)dt and its Young’s complementary function Ψ1,2(x)=ψ1,2(t)dt,respectively.

Remark 2.2It is shown in Lemma 2.1 thathas finite upper index,then the inverse functionexists and it has the form

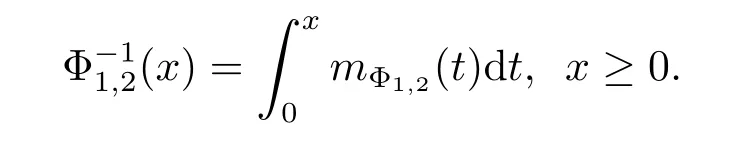
Since Φ1,2(x)is convex,then its inverse function(x)is concave,therefore mΦ1,2(x)is a decreasing function and we also have that

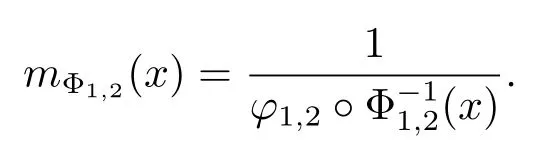
Lemma 2.2(see[6])Let Φ∈Δ2,then there exists a constant KΦ≥1 depending only on Φ,such that

Let v=(vn,n∈N)be a process adapted to(Fn,n∈N),the martingale transform Tvfor a given martingale f is defined by Tvf=(Tvfn,n∈N)where Tvfn:=vi-1·dfi.It can easily be seen that Tvf is still a martingale.

The Lemma below is well known and can be found in Long[7]and Weisz[11].

Lemma 2.3(see[7,13])Let f=(fn,n∈N)be a martingale.Then fnconverges a.s. on the set of{ω:s(f)＜∞}.

3 Main Results and Their Proofs

At first,we prove a necessary lemma,which can be seen as a weak version of the generalized Hlder’s inequality and has an independent existence value.

Lemma 3.1Let Φ1be a concave Young function with qΦ1＞0,Φ2a concave Young function with qΦ2＞0 or a convex Young function with pΦ2＜+∞,and let Φ1Φ2, Φ1,2(x)=◦Φ2(x)with Young’s complementary function Ψ1,2(x).If f∈wLΦ2,g∈wLΦ1◦Ψ1,2,then f·g∈wLΦ1and we have

ProofFor any f∈wLΦ2and g∈wLΦ1◦Ψ1,2,if‖f‖wLΦ2·‖g‖wLΦ1◦Ψ1,2=0,then(3.1) is obvious.Now we assume that‖f‖wLΦ2·‖g‖wLΦ1◦Ψ1,2＞0.For the sake of convenience, denote‖f‖wLΦ2=A and‖g‖wLΦ1◦Ψ1,2=B.Because(Φ1,2,Ψ1,2)is a pair of conjugate Young functions,by Young’s inequality,we have that

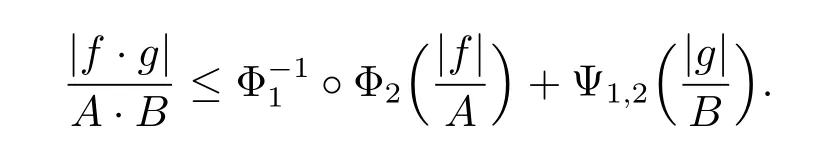
Since qΦ1＞0 and 0＜qΦ2≤pΦ2＜+∞,Φ1,Φ2∈Δ2.Applying Lemma 2.2,we obtain

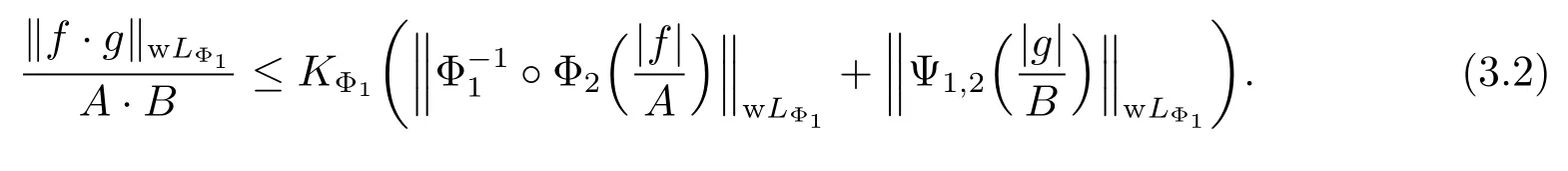
Because 0＜A=‖f‖wLΦ2＜+∞,so Φ2P(|f|＞t)≤1 for all t＞0.Since both Φ1and Φ2are continuous and bijective from[0,+∞)to itself,then for any s＞0,there exists a t＞0 such that Φ1(s)=Φ2(t/A).Moreover,for any s＞0,we have

Theorem 3.1Let Φ1be a concave Young function with qΦ1＞0,Φ2a concave Young function with qΦ2＞0 or a convex Young function with pΦ2＜+∞,and Φ1Φ2.Let f=(fn,n∈N)∈wHΦ1,and define the martingale transform T(f)by

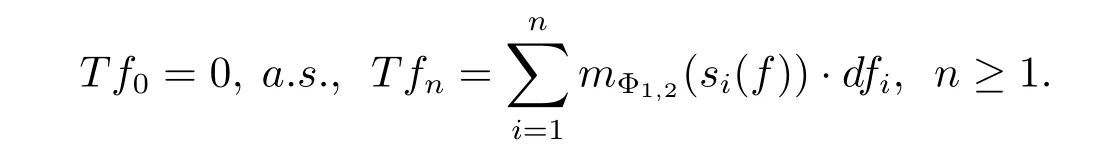
Then the martingale T(f)=(Tfn,n∈N)belongs to wHΦ2and Additionally,{Tfn}n≥1converges a.s.to a limit Tf∞.

ProofSetting s0(f)=0,for all i≥1,we have E(|dfi|2|Fi-1)=(f),and

Then for all n≥1,we have

The sequence{sn(f)}n≥1is non-negative and non-decreasing,the function mΦ1,2(x)is nonnegative and decreasing,so for all i≥1,we have

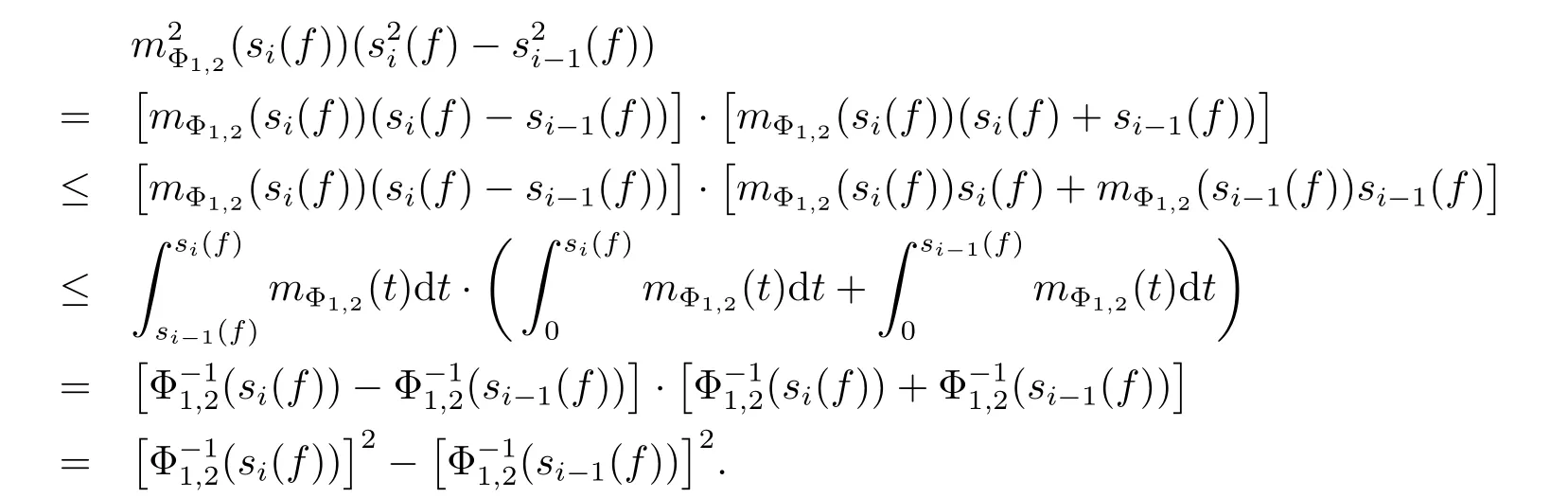
Consequently,for any n≥1,we get

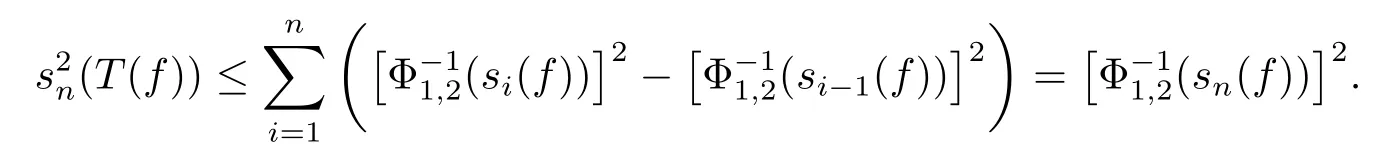
In other words,we have that s(T(f))≤(s(f))a.s..Given f∈wHΦ1,then‖s(f)‖wLΦ1=‖f‖wHΦ1＜+∞.By the homogeneity of quasi-norm,we may assume that‖s(f)‖wLΦ1=1 for simplicity.Then

Since both Φ1and Φ2are bijective from[0,+∞)to itself,for any s∈(0,+∞),there exists a t∈(0,+∞),such that Φ1(t)=Φ2(s).For any s＞0,we have that

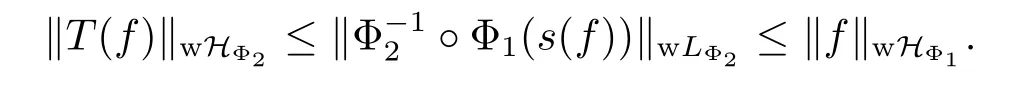
The inequality(3.3)is proved.

On the other hand,since s(T(f))≤◦Φ1(s(f)),then{s(T(f))＜+∞}Φ1(s(f))＜+∞}.Hence,we have that

This means that s(T(f))＜+∞a.s..Consequently,by Lemma 2.3,{Tfn}n≥1converges a.s. to a limit Tf∞.The proof is completed.

Theorem 3.2Let the generalized Young functions Φ1and Φ2,the martingales f and T(f)be as in Theorem 3.1.Then

ProofWith s0(T(f))=0,we have

for all i≥1.From the representation of Tfnfiguring in the statement of Theorem 3.1,we have

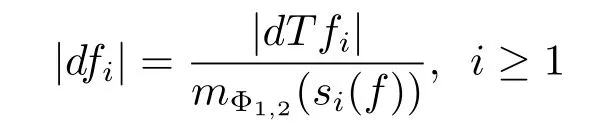
(if mΦ1,2(si(f))=0,then we can add an ε＞0 to each si(f)and at the end let ε→0). Therefore,by Abel’s rearrangement,we have

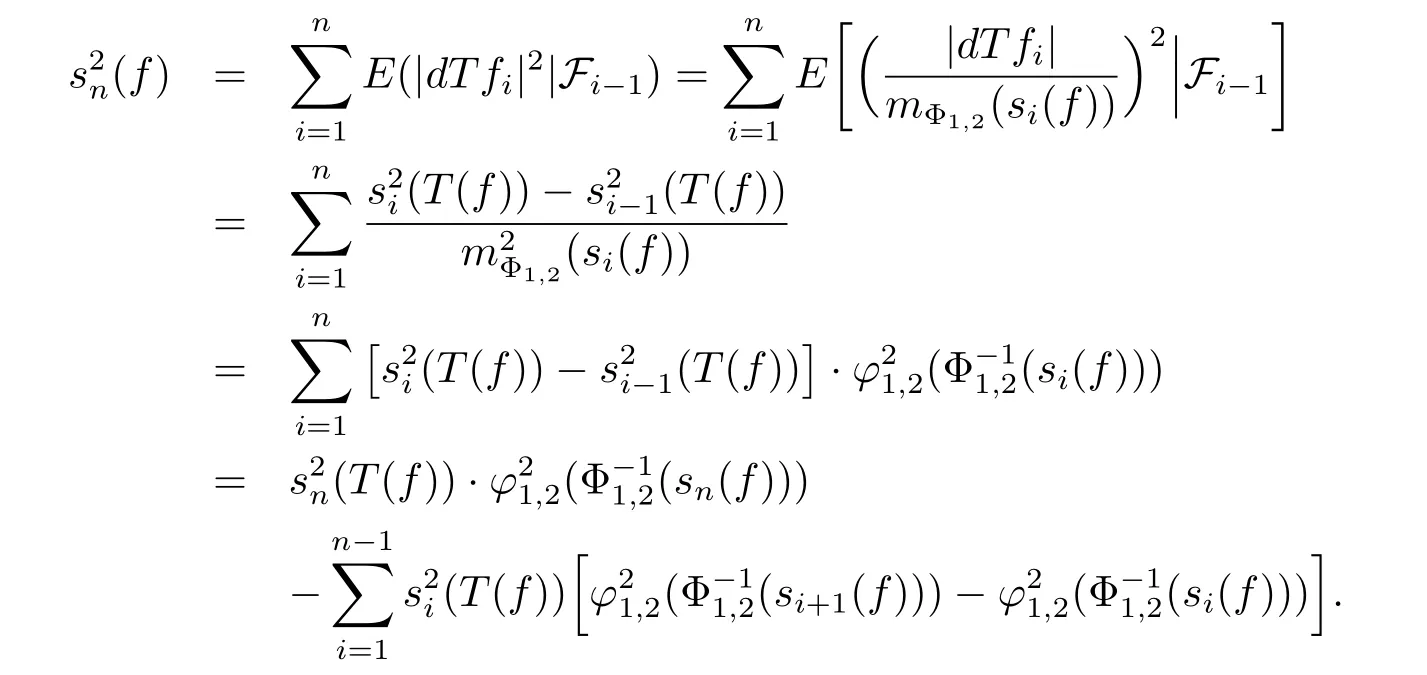
Noticing that both the sequences{sn(T(f))}n≥0and{φ1,2◦Φ-11,2(sn(f))}n≥0are nonnegative and nondecreasing,then we get that

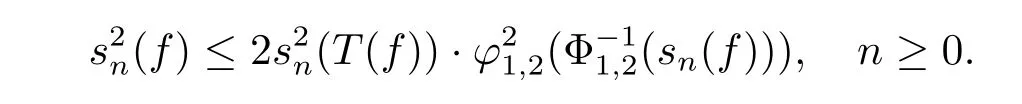
Therefore

Thus applying Lemma 3.1,we have that

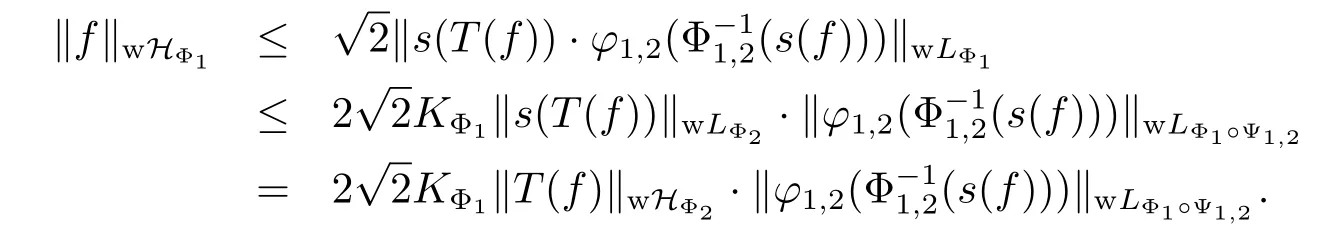
This proves the assertion.

Now,combining Theorem 3.1 and 3.2,we obtain the following corollary,one of the main results of the present article.

Corollary 3.1Let Φ1be a concave Young function with qΦ1＞0,Φ2a concave Young function with qΦ2＞0 or a convex Young function with pΦ2＜+∞,and Φ1Φ2.Then for any martingale f=(fn,n∈N)∈wHΦ1,there exists a martingale g=(gn,n∈N)∈wHΦ2, such that f is the martingale transform of g.Namely,we have

where vi=(i=0,1,2,3,···).We have

and

ProofFrom Theorem 3.1 and 3.2,only the inequality(3.4)needs to be proved.In fact,since(Φ1,2,Ψ1,2)is a pair of conjugate Young functions,so

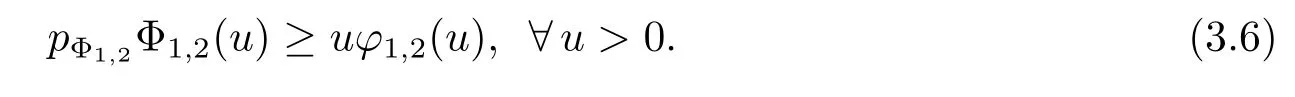
By(3.5)and(3.6),we get

and then

Employing(3.8),on the one hand,by the convexity of Ψ1,2,for all t＞0,we have

On the other hand,for any t＞0,we have

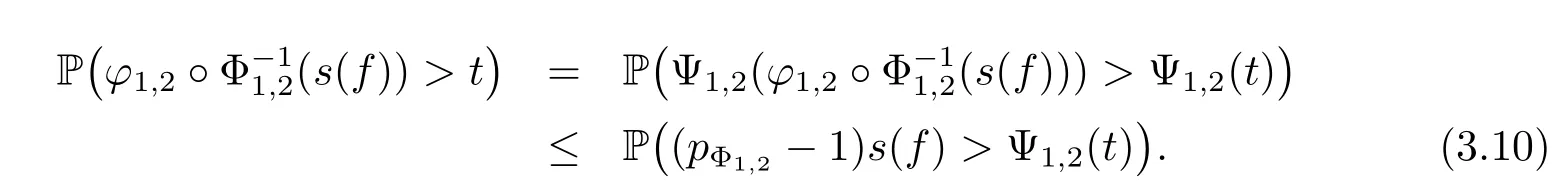
Since f∈wHΦ1,we have s(f)∈wLΦ1,furthermore,we have(pΦ1,2-1)s(f)∈wLΦ1too,and‖(pΦ1,2-1)s(f)‖wLΦ1=(pΦ1,2-1)‖s(f)‖wLΦ1=(pΦ1,2-1)‖f‖wHΦ1.Therefore for any u＞0,we have

From(3.9),(3.10)and(3.11),for any t＞0,we have that

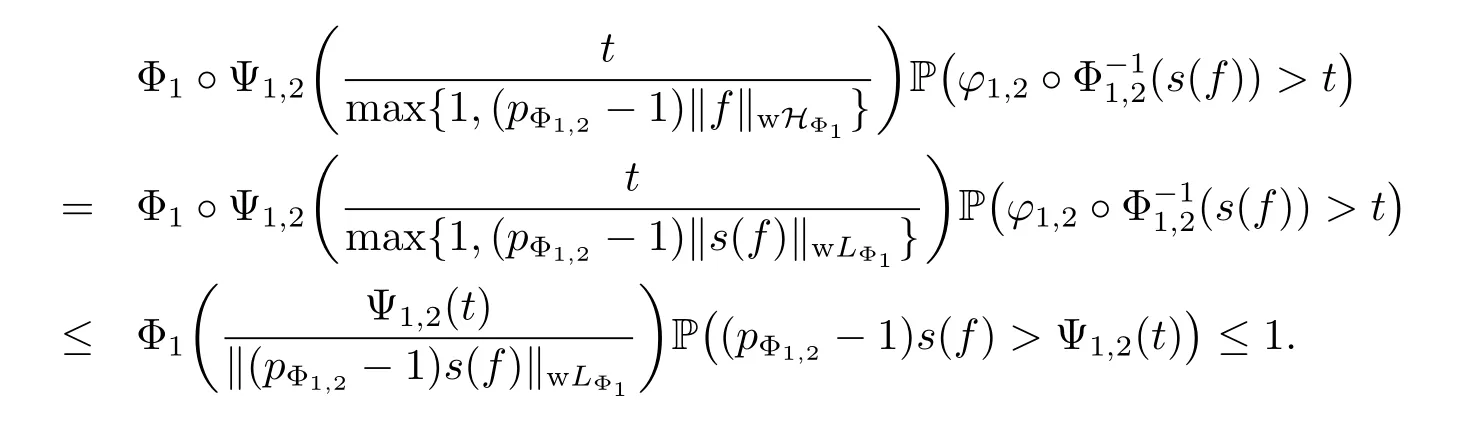
This implies that

[1]Burkholder D L.Martingale transforms[J].Ann.Math.Stat.,1966,37:1494–1504.

[2]Chao J A,Long Ruilin.Martingale transforms and Hardy spaces[J].Prob.The.Rel.Fiel.,1992,91: 399–404.

[3]Garsia A M.Martingale inequalities,seminar notes on recent progress[M].Math.Lect.Notes Ser., New York:Benjamin Inc,1973.

[5]Jiao Yong.Embeddings between weak Olicz martingale spaces[J].J.Math.Anal.Appl.,2011,378: 220–229.

[6]Liu Peide,Hou Youliang,Wang Maofa.Weak Orlicz spaces and its applications to the martingale theory[J].J.Sci.China,Ser.A,2010,53:905–916.

[7]Long Ruilin.Mart spaces and inequalities[M].Beijing,Wiesbaden:Peking Univ.Press Vieweg Publ., 1993.

[8]Meng Weiwei,Yu Lin.Martingale transform between Q1and QΦof martingale spaces[J].Stat.Prob. Lett.,2010,79:905–916.

[9]Nakai E.On generalized fractional integrals on the weak Orlicz spaces,BMOΦ,the Morrey spaces and the Campanato spaces[A].In function spaces,interpolation theory and related topics[C].Berlin, New York:Lund,Walter de Gruyter,2000:389–401.

[10]Weisz F.Hardy spaces of predictable martingales[J].Anal.Math.,1994,20:225–233.

[11]Weisz F.Martingale Hardy spaces and their applications in Fourier analysis[M].Lect.Notes Math., Vol.1568,New York:Springer-Verlag,1994.

[12]Weisz F.Weak martingale Hardy spaces[J].Prob.Math.Stat.,1998,18:133–148.

[13]Weisz F.Bounded operators on weak Hardy spaces and applications[J].Acta Math.Hung.,1998, 80:249–264.

[14]Yu Lin.Martingale transforms between Hardy-Orlicz spaces QΦ1anf QΦ2of martingales[J].Stat. Prob.Lett.,2011,81:1086–1093.

[15]Yu Lin,Zhuang Dan.Martingale transforms between Orlicz-Hardy spaces of predictable martingales[J].J.Math.Anal.Appl.,2014,413:890–904.

[16]Yin Huan,Yu Lin.Martingale transforms and Orlicz-Hardy spaces associated with concave functions [J].Acta Anal.Funct.Appl.,2015,17:209–219.

凹函数定义的弱Orlicz-Hardy空间之间的鞅变换

郭红萍1,于林2,姜琴3

(1.汉江师范学院数学与财经系,湖北十堰442000)

(2.三峡大学理学院,湖北宜昌443002)

(3.汉江师范学院计算机科学系,湖北十堰442000)

本文研究了两个弱Orlicz-Hardy鞅空间中元素之间相互转换关系的问题.利用鞅变换的方法,证明了:设Φ1是凹Young函数,Φ2是凹或者凸Young函数,且qΦ1＞0,0＜qΦ2≤pΦ2＜+∞,则当Φ1Φ2时,wHΦ1中的元素是wHΦ2中元素的鞅变换的结果,所得结果将已有的相关结论由强型空间(赋范空间)推广到弱型空间(赋拟范空间).

鞅变换;弱Orlicz-Hardy空间;凹函数

O211.6

tion:60G42

A

0255-7797(2017)01-0001-10

∗Received date:2016-04-30Accepted date:2016-06-28

Foundation item:Supported by the Science and Technology Research Program for the Education Department of Hubei Province of China(Q20156002).

Biography:Guo Hongping(1987–),female,born at Xiantao,Hubei,lecturer,major in martingale theory and functional analysis.