基于复杂网络拓扑结构的评估体系研究
邵铁林
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
基于复杂网络拓扑结构的评估体系研究
邵铁林
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
对复杂网络拓扑结构中特定属性的计算和评估进行了研究。层次分析法和熵权法被用来计算复杂网络拓扑结构的权重,这样既可以防止在主观赋权法上因专家经验不足使得对方案的排序造成很大的随意性,又可以避免客观赋权法的结果与实际情况不一致的现象发生。选取了规则网络模型、随机网络模型、小世界网络模型和BA无标度网络模型进行加权计算,并计算出它们各自相应的综合权重。从综合权重的角度来看,实验结果表明,随机网络效能最好,接下来是小世界网络、无标度网络,最后是规则网络。该评估体系和算法可以被广泛地用于需要对网络性能进行定量评估的情况下。
主观赋权法;客观赋权法;组合赋权法;网络性能评价
0 引言
目前对多属性决策问题的权重确立已有许多方法,如何准确地对各个指标赋值,会直接影响到最终复杂网络系统综合权重结果的正确性。根据确定指标权重方法的不同,可以分为主观赋权法、客观赋权法和主客观相结合的组合赋权法。主观赋权法是由决策者的偏好给出的方法,如专家调查法[1-2]、层次分析法[3-4]、二项系数法[3]等都可以用来对复杂网络进行系统评估。但是主观赋权法有它自身的缺陷。比如由专家根据自己的经验和判断对目标赋以权值时,得到的不同方案之间的排序会出现一个很大的随意性。客观赋权法是一种基于目标矩阵信息的方法,如熵权法[4]、离差及均方差法[5]等。但由于该方法没有体现出决策者对诸多目标的重视程度,因此一些可以使不同方案显示出明显差异的目标,并没有体现其重要性,甚至会出现截然相反的结果。
本文运用了第三种赋权方法:主客观组合赋权法[6]。主客观组合赋权法正好可以克服主观的随意性并避免客观所得结果与实际不符的现象发生,可以使复杂网络系统最终得到的综合权重结果科学合理。在本文中,综合了主观赋权法中的层次分析法和客观赋权法中的熵权法。列举四种基本的复杂网络模型:规则网络模型[7]、随机网络模型[8]、小世界网络模型[9]和BA无标度网络模型[10]。在同样目标条件下根据最终所得的综合权值的大小对不同的复杂网络模型进行排序。
1 复杂网络拓扑结构模型的指标确立[11]
影响复杂网络模型的因素有许多,应该尽可能选取少量但具有关键性的指标。在这里选取了鲁棒性、可靠性、适应性和品质因素作为复杂网络模型的评估指标。各指标的建立如图1~图4所示。

图1 鲁棒性评价指标图

图2 可靠性评价指标图

图3 适应性评价指标图

图4 品质因素评价指标图
2 基于AHP层次分析法的指标权重计算方法
层次分析法其主要思想是将要达到的目标分解为多个具有代表性的指标,根据指标间的从属性关系建立一个递接层次结构模型,按层进行分析,最终获得底端层指标相对于目标层的最终权重。
AHP法可分为4个步骤:
(1)根据复杂网络系统中各因素之间的关系,将网络分为3个层次,即目标层、准则层和措施层,并建立层次结构。
(2)对于同一层中各因素相对于上一层因素的重要性进行两两比较,构造权重判断矩阵。
(3)由判断矩阵计算得到各指标的权重,并进行一致性检验。其具体步骤如下:
①计算判断矩阵的每一列,并进行规划处理
②对判断矩阵每一行进行求和

W=[W1,W2,…,Wn]T,即为所求特征向量。
④计算判断矩阵的最大特征根
其中A是权重比矩阵。
(4)措施层的权重计算:
①准则层的权重为:w=(w1,w2,w3...wk)T,其中,wi为准则层指标i在准则层中所占有的相对权重。
②措施层指标权重为:wk=(wk1,wk2,wks…wkp)T,再以wk为列向量构成矩阵W=[w1,w2,…wn]。
③措施层的权重为:c=W·w,其中c为最终的权重值。
3 基于熵权法的指标权重计算方法
熵最早是用来描述热力学第二定律,在1865年由克劳休斯引入。信息熵值反映了信息的不确定程度,可以度量信息量的多少。在复杂网络效能评估时某一项指标带有的信息量越多,表明该项指标对决策的作用越大,此时信息熵值越小。因此,可用信息熵评价所获信息的有序度及其效用,即各评价指标的权重大小由评价指标值构成的判断矩阵来确定。
熵权法的具体计算步骤如下:
(1)设一共有M个方案,本文中共有4个复杂网络模型M=(M1,M2,M3,M4)。评价指标D=(D1,D2,D3,D4),被评价的对象Mi对指标Dj的值记为Xij(i=1,2,3,4;j=1,2,3,4)。则形成的原始数据矩阵如下:
其中Xij为第j个指标下的第i个评价对象的值。
(2)对原始矩阵进行无量纲化处理,所得到的指标值越大表明评价对象在该项目上表现越好:

(4)计算第j项指标的熵值ej
其中,m为方案的个数,本文中共有4个方案,所以m=4。
(5)计算第j项指标的差异系数dj
dj=1-ej
dj越大,该指标所提供的信息量越大,越应该给予较大的指标权重。
(6)确定各指标的熵权
(7)分别计算各个评价对象的综合评价值
4 组合赋权法计算权重


采用拉格朗日乘子法解决上述优化问题:
5 应用实例
本文采用4种复杂网络模型,它们对应着4个方案。分别是A:无标度网络;B:小世界网络;C:随机网络;D:规则网络。
基于层次分析法的效能评估,根据第2节中所提到的方法,通过MATLAB来进行计算。以4种不同的复杂网络模型为4种方案得到的各自指标权重,见表1~表4。

表1 实验A的仿真结果(无标度网络模型)

表2 实验B的仿真结果(小世界网络模型)
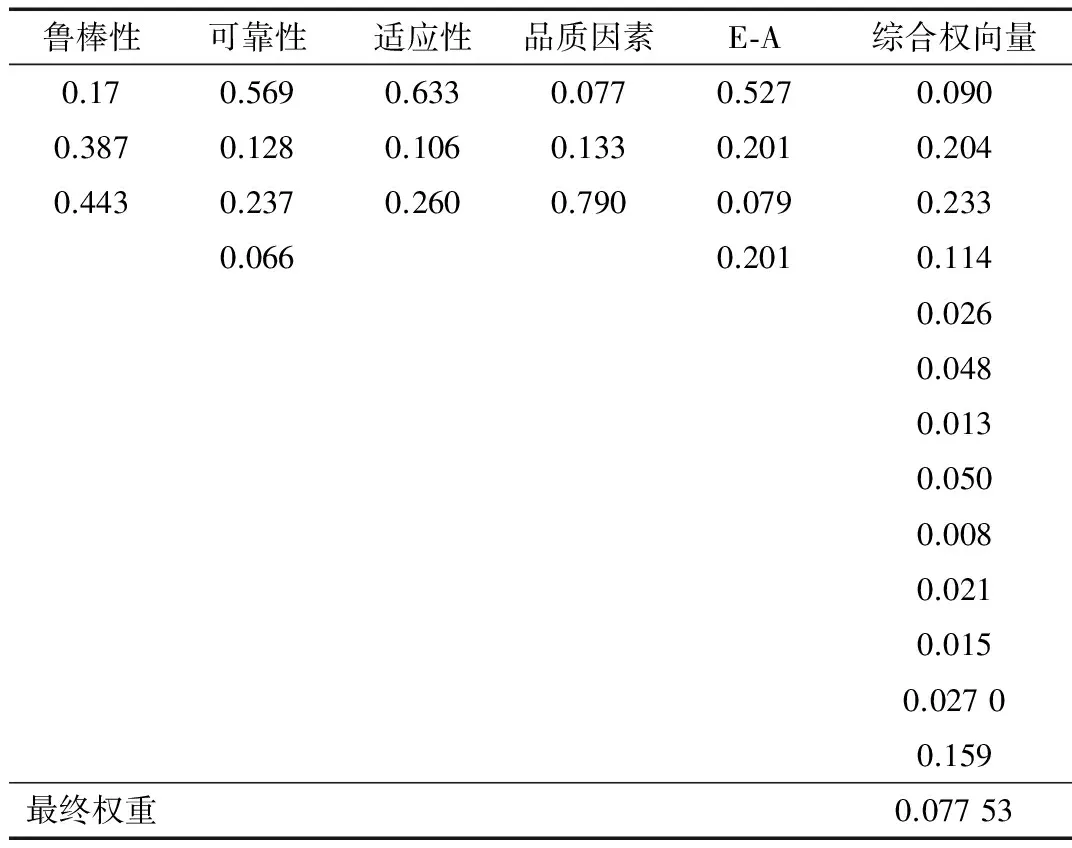
表3 实验C 的仿真结果(随机网络模型)

表4 实验D 的仿真结果(规则网络模型)
最终通过层次分析法得到的4种方案的综合权重为:Wi=[0.076 84,0.077 07,0.077 53,0.075 07]。
根据第3节介绍的熵权法,将鲁棒性、可靠性、适应性、品质因素设为4个评价指标D=(D1,D2,D3,D4),对于4种复杂网络模型设定为4个不同的评价对象M=(M1,M2,M3,M4)。形成的判断矩阵为:

最后得到的4种复杂网络模型的权值向量为:
Vi=[0.240 42,0.256 04,0.276 52,0.227 02]
根据第4节介绍的组合赋权法,将层次分析法和熵权法的权重带入组合赋权法的公式得到4种复杂网络模型的效能权重。
A:W1=0.438 84
B:W2=0.524 27
C:W3=0.639 87
D:W4=0.350 89
最终根据组合赋权法得到了4种复杂网络模型的权重,充分利用了两种方法的优点,同时又最大程度地避免了人为主观性和客观单一权重的片面性,使得综合评价既合理又科学。根据组合赋权法得到4种方案各自的权重大小,对4种复杂网络模型的效能进行排序,得到的结果是:C>B>A>D。即随机网络的效能要好于小世界网络,小世界网络要好于无标度网络,而规则网络的效能最差。结论符合实际情况,因此该评估系统可靠有效。
6 结论
在对复杂网络拓扑结构进行效能评估时,利用将主观赋权法和客观赋权法相结合的思想,把层次分析法和熵权法的各自权重进行了科学、合理的结合。这既反映了专家对各评价指标的主观意向,又包含了科学严谨的数学理论依据,便于计算处理。组合赋权法使得主观判断和客观计算有了一个很好的结合。
[1] 聂相田,王博,骆原. Delphi专家法在施工监理规范修订中的应用[J]. 人民黄河,2010,32(12):240-242,247.
[2] 房鑫,郝艳华,吴群红,等. 基于Delphi法的完善全民医保制度要素设计专家意见分析[J]. 中国卫生经济,2016,35(2):29-31.
[3] 肖满生,阳娣兰,张居武,等. 基于模糊相关度的模糊C均值聚类加权指数研究[J]. 计算机应用,2010,30(12):3388-3390.
[4] 毛毅钢. 基于熵权法的高校体育教师评价指标体系的建立[J]. 重庆理工大学学报(自然科学版),2015,29(1):150-154.
[5] 雷勋平,刘晨. 熵权法在高校实践教学质量评价中的应用[J]. 蚌埠学院学报,2015,4(6):125-128.
[6] 谢轶. 组合赋权法确定清河流域总量减排绩效评估指标权重[J]. 环境保护科学,2014,40(1):28-31.
[7] 王晨晨,姚军,杨永飞,等. 基于规则网络的碳酸盐岩多尺度网络模型构建方法研究[J]. 计算力学学报,2013,30(2):231-235.
[8] 姜志宏,王晖,高超. 一种基于随机行走和策略连接的网络演化模型[J]. 物理学报,2011,60(5):824-832.
[9] 张浩. 基于小世界网络的高校知识转移机理及扩散模型研究[J]. 情报科学,2011(9):1294-1297,1312.
[10] 吴泓润,覃俊,易云飞,等. 基于优化理论的社区无标度网络模型[J]. 计算机学报,2015,38(2):337-348.
[11] 刘建香. 复杂网络及其在国内研究进展的综述[J]. 系统科学学报,2009,17(4):31-37.
Research on the assessment system based on complex network topological structures
Shao Tielin
(College of Information Science and Engineering, Shenyang Ligong University, Shenyang 110159, China)
A quantitative way of measuring and evaluating specific properties in complex networks topology is studied. By determining the weight of the complex network topology structure, both hierarchy process and entropy weight method were introduced to avoid incorrect results out of great randomness caused by experts who are lacking of experiences in the subjective weighting method, as well as to avoid the inconsistent output of objective weighting method with that of the real situations. Weighting method was performed on four different complex networks models including regular network model, random network model, small world network model and BA scale-free network model, and comprehensive weights of corresponding networks were calculated. The experimental results show that on comprehensive performance point of view, random network is the best followed by small world network, scale free network rank next and the regular network at last. The assessment systems and algorithms could be widely used in circumstances where quantitative evaluations of networks performances are required.
subjective weighting method; objective weighting method; combined weighting method; network performance evaluation
TP302.7
A
10.19358/j.issn.1674- 7720.2017.01.021
邵铁林. 基于复杂网络拓扑结构的评估体系研究[J].微型机与应用,2017,36(1):69-72.
2016-08-05)
邵铁林(1990-),男,硕士研究生,主要研究方向:无线网络信息处理技术。

