基于IFOA-KELM-MEA模型的游梁式抽油机采油系统井下工况的短期预测

李琨，韩莹，佘东生，魏泽飞，黄海礁

（1渤海大学工学院，辽宁 锦州 121013；2辽河油田分公司锦州采油厂采油作业五区，辽宁 锦州 121209）

基于IFOA-KELM-MEA模型的游梁式抽油机采油系统井下工况的短期预测

李琨1，韩莹1，佘东生1，魏泽飞1，黄海礁2

（1渤海大学工学院，辽宁 锦州 121013；2辽河油田分公司锦州采油厂采油作业五区，辽宁 锦州 121209）

实现对井下工况的预测是及时掌握抽油井生产状态的有效方法，对提高油井生产效率和降低维护成本具有十分重要的意义。采用混沌理论实现抽油井井下工况的短期预测，首先将所提取的示功图的不变曲线矩特征向量作为预测变量，在证明其数据序列具有混沌特性后，由核极限学习机（kernel extreme learning machine, ELM）建立混沌时间序列预测模型，对其中的几个不确定参数采用改进的果蝇优化算法（improved fruit fly optimization algorithm, IFOA）进行优化选取，IFOA采用全局群体多样进化和局部个体随机变异的策略，最后，对模型所预测的结果进行物元分析（matter-element analysis, MEA），诊断其属于哪种故障类型。由某油田作业区的两口生产井进行实例验证，结果表明所提出的IFOA-KELM-MEA预测模型是合理有效的。

混沌时间序列预测；游梁式抽油机；核极限学习机；果蝇优化算法；物元分析；测量；石油；模型

引 言

游梁式抽油机采油系统是目前国内外油田的主要生产方式，依靠抽油杆的上下移动带动井下抽油泵将油液抽出地面。系统主要由两个部分组成，其中，地上部分主要包括电动机、皮带轮-齿轮箱、四连杆机构等；地下部分主要包括抽油杆、抽油泵、油管、套管等。由于地下部分工作在不易观察的地面以下，特别是抽油泵工作在数千米的地下，工作环境恶劣，造成井下工况复杂且不确定性较强。根据目前的生产现状，典型的井下工况类型有：“供液不足”“气体影响”“抽油杆断落”“油稠”“游动凡尔漏失”“固定凡尔漏失”“泵上碰”“泵下碰”“油井出砂”和“柱塞脱出工作筒”等，不同的工况发生程度对采油系统的影响不同，会造成减产、高能耗甚至停井修井等问题。

在油田实际生产中，通过采集抽油井的示功图分析井下的工况类型，示功图是抽油杆光杆位移变化在一个完整周期内载荷-位移数据所构成的二维关系曲线。示功图的形状可以反映不同的工况类型[1]，例如：“正常”的图形特征是“上、下趋近于平行，左右趋近于平行”，“供液不足”的图形特征是“图形右下部分缺失，加载线正常，卸载线变化较慢”，“油井出砂”的图形特征是“出现锯齿状波峰，尖小且变化快”。对于示功图的分析，传统的方法是依靠技术人员进行人工识别，再根据结果调整生产措施；近年来，随着计算机信息技术的不断发展以及油田生产对先进技术要求的不断提高，基于计算机的智能分析方法越来越受到关注。文献[2]提出基于 FBH-SC聚类的抽油井井下故障诊断方法，不依赖训练样本，以一种无监督学习的方式实现井下工况的诊断；文献[3]提出一种有杆抽油系统井下工况诊断方法，分析井下泵功图阀门打开和关闭点间的曲线段，将曲线段的曲率特征作为分类依据，建立了16个井下工况类别的Mamdani模糊推理系统；文献[4]提出基于示功图的有杆抽油系统故障递阶诊断方法，通过分析故障机理，建立有杆抽油系统故障识别的搜索树，对故障样本进行故障类型的详细识别；文献[5]提出基于生物地理优化算法的抽油机故障诊断方法，将混沌变异算子与生物地理优化算法相结合，对BP神经网络的相关参数进行优化选取，用于抽油机的故障识别；文献[6]采用基于曲线矩和PSO-SVM的方法实现有杆泵抽油系统井下工况的诊断，提取示功图的曲线矩特征向量作为诊断模型的输入向量，建立PSO-SVM模型实现井下工况的识别；文献[7]考虑井下多工况共存时的诊断，提出一种基于Freeman链码和指定元分析的多故障诊断方法，由Freeman链码表示示功图，提取其特征向量，再根据指定元分析方法实现多故障识别。

根据目前的研究现状，对于游梁式抽油机采油系统井下工况的诊断，主要针对系统当前工况发生时的状态评价及定位，而对井下工况预测的研究却鲜有涉及。然而在实际生产中，对于一些工况类型来说，如果不能做出提前预测，当发现时系统生产已经偏离正常水平，虽然管理者可以通过调整生产措施使其恢复到正常水平，但已严重影响了生产的经济效益；而对于另一些工况类型来说，如果不能做出提前预测，当发现时已使系统生产处于负面甚至危险的境地，此时管理者很难将系统工况恢复到正常水平。对此，本文对游梁式抽油机采油系统井下工况的短期预测方法展开研究，主要解决两个问题：一是如何建立合理的预测模型，二是如何确定预测后的工况类型。

采用非线性建模和线性关联相结合的策略，首先对所提取的示功图的特征向量序列进行混沌特性分析，然后由核极限学习机建立混沌时间序列预测模型，对于不确定的模型参数采用改进的果蝇优化算法进行优化选取，最后根据物元分析理论将预测结果与工况类型进行线性关联，以判断预测后的工况类型。

1 示功图特征提取

游梁式抽油机采油过程是一个连续的生产过程，井下工况的变化可以体现在示功图形状的不断变化上，因此，可以对示功图图形形状进行数字化特征提取，将其特征向量作为预测模型的输入。采用文献[1]的特征提取方法，首先将采集的地面示功图转化为井下泵功图，然后将其划分为4个区域，如图1所示，然后提取每一区域的7个不变曲线矩特征向量，将28个不变曲线矩特征向量作为表达示功图图形特征的特征向量。鉴于篇幅原因，基于曲线矩的示功图特征提取的相关内容不再过多赘述。

2 示功图特征向量的混沌特性分析

要实现游梁式抽油机采油系统井下工况的短期预测，需要首先对所提取的28个示功图的不变曲线矩特征向量数据序列分别进行混沌特性分析，只要能够证明它们具有混沌特性，就可以采用预测模型进行预测。采用0-1混沌测试法[8-9]进行不变曲线矩特征向量数据序列的混沌特性分析，下面对 0-1混沌测试法的原理进行简要介绍。

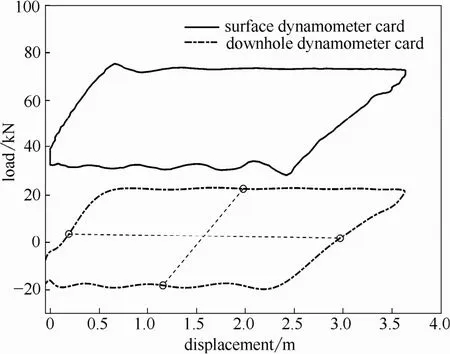
图1 示功图特征提取Fig.1 Feature extraction of dynamometer card

设示功图的不变曲线矩特征向量数据序列为fi(j)（i=1, 2,…, 28；j=1 ,2,…, N），一随机常数c∈(0, π)，定义如下2个函数pi,c(n)和qi,c(n)有

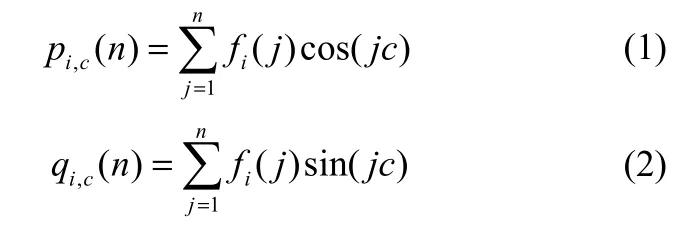
其中，i=1, 2,…, 28；n=1, 2,…, N。

由pi,c(n)和qi,c(n)计算均方位移Mi(n)如下

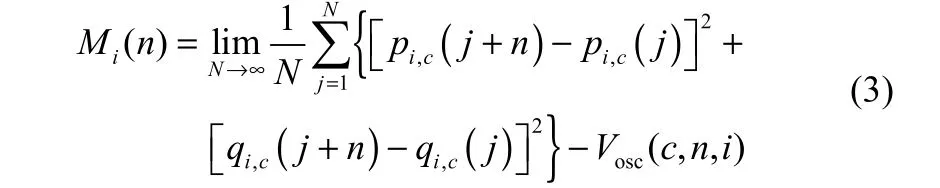
其中，Vosc(c,n,i)为摄动项，定义如下

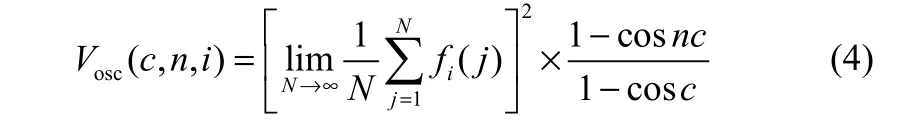
采用文献[8]中的回归分析方法计算均方位移Mi(n)的渐近增长率Ki,c如下

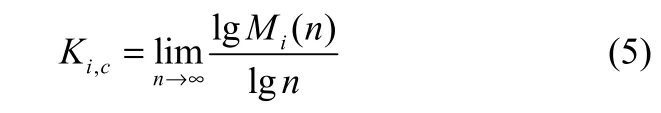
为了减小计算偏差，在(0, π)取值范围内随机重复选择Nc次常数c，每一次重复计算式(1)～式(5)，然后取Nc个Ki,c值的均值i,c，取Nc=100。根据文献[10-11]，若i,c≈1，表明该时间序列具有混沌特性；若i,c≈ 0，表明该时间序列不具有混沌特性。

在实际计算过程中，pi,c(n)和qi,c(n)可以通过如下迭代计算得到[8]

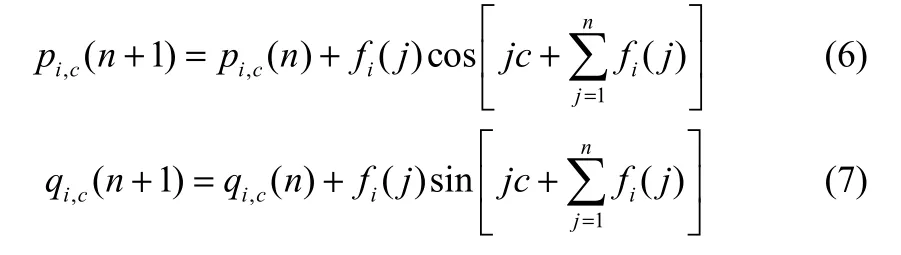
其中，j=1, 2,…, N；n=1, 2,…, N。

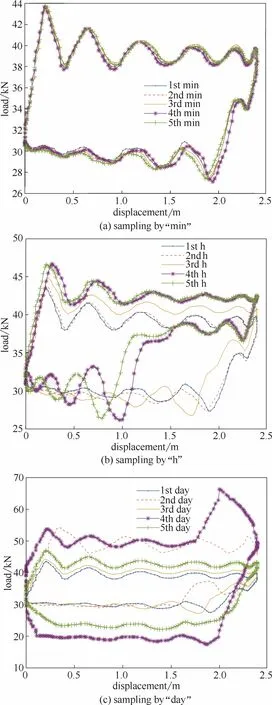
图2 不同采样时间间隔下的示功图变化趋势图Fig.2 Changing trends of dynamometer card under different sampling time intervals

在实现过程中采用迭代方式计算均方位移Mi(n)和渐近增长率Ki,c时，采用如下限定条件[8]：n≤N/10，为了计算方便，设定n=N/10。

以国内某油田作业区一口抽油井的实际生产数据进行验证，当该油井的冲程为2.5 m和冲次为3次·min−1时，根据安装在油井“驴头”悬点处的示功图采集设备的工作方式，对油井示功图进行连续采集，采集频率为每分钟3幅示功图，每幅示功图由250组数据点组成。在采用时间序列方法进行预测时，样本点的采样时间间隔的选择较为重要，分别以“分钟（min）”、“小时（h）”和“天（day）”为采样时间间隔的5幅示功图如图2所示。

由图2可以看到，当以“分钟”为采样时间间隔采集数据时，由于采样间隔过短，示功图的变化不明显，由此数据构成时间序列进行预测意义较小；当以“天”为采样时间间隔采集数据时，由于采样间隔过长，示功图的变化幅度较大，中间过程的很多有用信息丢失，由此数据构成时间序列的可预测性较差；而以“小时”为采样时间间隔采集数据时，所构成的时间序列既能兼顾数据的变化趋势，又不易丢失变化过程的有用信息。因此，所采用的实际示功图数据以“小时”为采样时间间隔，即两幅示功图之间的时间间隔为1 h。

以“小时”为采样时间间隔连续采集该抽油井一段生产周期内的228幅示功图，首先采用第2节的特征提取方法分别提取228幅示功图的28个不变曲线矩特征向量，然后构成28个不变曲线矩特征向量数据序列，每个序列包含228个数据点。下面以第12个不变曲线矩特征向量为例，采用0-1混沌测试法进行混沌特性分析。第12个不变曲线矩特征向量数据序列如图3所示。

根据式(1)～式(7)，由 0-1混沌测试法对第 12个不变曲线矩特征向量数据序列进行混沌特性分析，得到p12,c(n)和q12,c(n)的相图如图4所示，100次重复计算后的平均均方位移M12(n)和平均渐近增长率12,c如图5所示。

图3 第12个不变曲线矩特征向量数据序列Fig.3 Data sequence of 12th invariant curve moments eigenvalue

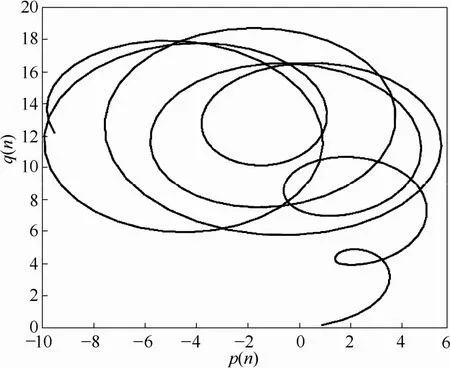
图4 p12,c(n)和q12,c(n)的相图Fig.4 Phase diagram of p12,c(n) and q12,c(n)

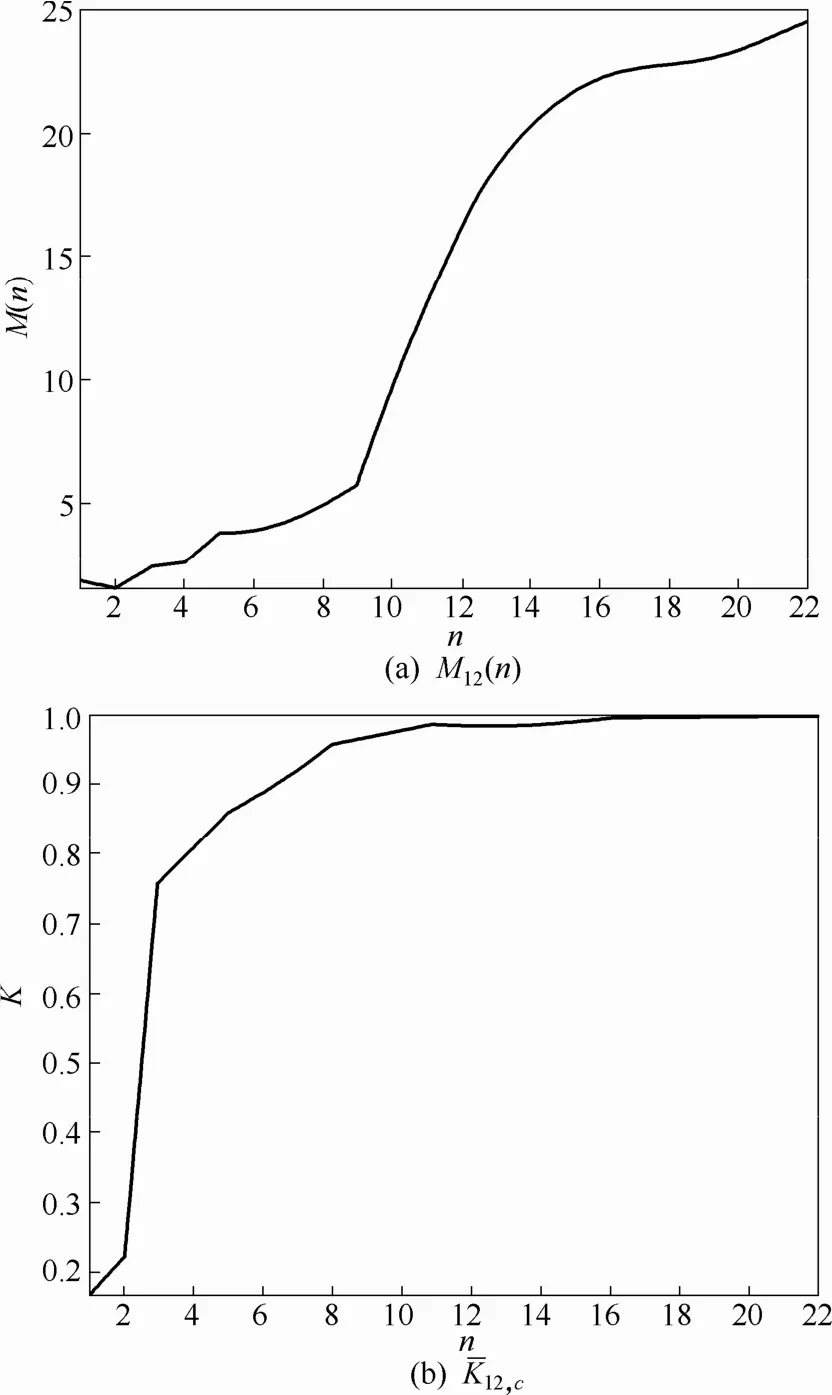
图5 平均均方位移和渐近增长率（100次重复计算）Fig.5 Mean-square displacement and progressive growth rate (average value of 100 times)

由图4、图5，p12,c(n)和q12,c(n)的相图呈现布朗运动特性，均方位移M12(n)呈线性增长变化，渐近增长率K的变化趋近于1，因此，可以证明第12个不变曲线矩特征向量数据序列具有混沌特性，可以建立预测模型进行预测。同理，根据式(1)～式(7)对其他不变曲线矩特征向量数据序列进行混沌特性的验证，都能证明满足混沌特性，鉴于文章篇幅原因，不再一一列举验证结果。

3 基于混沌时间序列的井下工况的短期预测

在验证了不变曲线矩特征向量数据序列具有混沌特性之后，就可以通过相空间重构进行预测。相空间重构是混沌时间序列预测最基础的第一步，它的基本思想是：系统中每一个变量的变化都会受到与之有联系的其他变量的影响，因此这些相关变量的信息就包含在任一变量的动态变化过程中，通过重构得到的相空间会反映系统状态的变化规律。

设不变曲线矩特征向量混沌时间序列为{xi(n), i=1, 2,…, 28, n=1, 2,…, N}，通过相空间重构得到如下形式

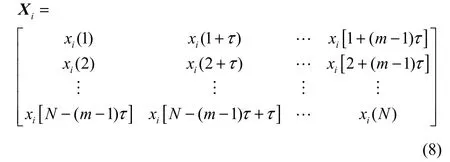
采用一步预测，即由一段时间的数据序列去预测下一个时间点的值，过长的预测步长会降低预测的精度。那么预测输出可以由如下形式进行表示

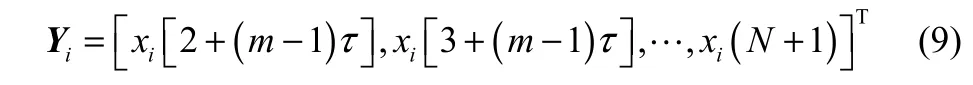
其中，m为嵌入维数，τ为延迟时间。m和τ是相空间重构中两个关键的参数，如果能够选取正确的值，则可以使重构的相空间在一定程度上逼近原始的系统。

将 Xi和Yi分别作为预测模型的输入和输出即可完成建模，采用核极限学习机作为混沌时间序列的预测模型。

4 核极限学习机（KELM）

极限学习机（extreme learning machine, ELM）是Huang等[12]在2006年提出的一种新型前馈神经网络模型，能够克服像BP神经网络等传统模型存在的收敛速度慢、易陷入局部最优、泛化能力差等不足[13]。对于给定的训练样本集{(xi,ti)|xi∈Rd,ti∈Rn,i=1,2,…, N}，ELM 模型的数学描述为：，其中，ti为ELM模型的训练输出；βj为隐含层神经元与第i个输出神经元之间的连接权值；ωj为隐含层神经元与输入神经元之间的连接权值；bj为第 j个隐含层神经元的偏置；L为隐含层节点的个数；g(·)为激活函数。ωj和 bj在系统初始化时随机给定，在模型训练过程中其值不发生变化。

ELM 模型训练的目的就是找到最优的输出权值矩阵β，使得||H·−βY||=0，其中：H为隐含层输出矩阵，Y为期望输出值矩阵。

采用如下公式求得β

其中，H+为隐含层输出矩阵H的伪逆[14]。

那么ELM模型的输出函数可以表示为[15]

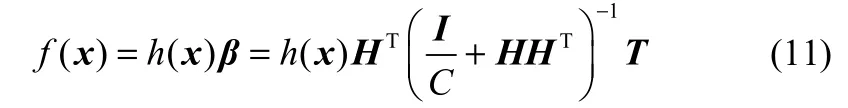
其中，C为正则化参数，T=[t1t2… tN]，h(x)=g(ω, b, x)。

对于式（11），当h(x)为未知的特征映射时，可以构建KELM模型，定义核矩阵形式如下[15]

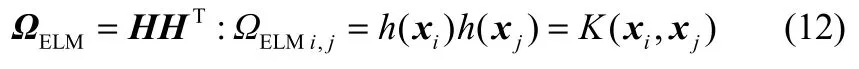
其中，i,j=1, 2, …, N。

那么，KELM模型的输出函数可以表示为

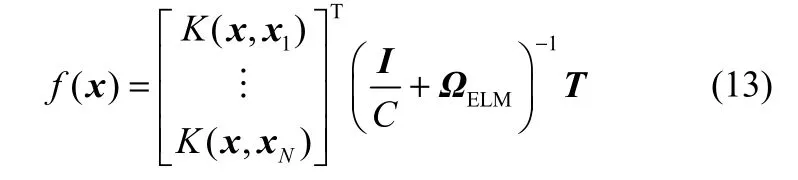
本文采用高斯核函数如下

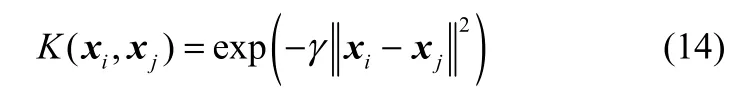
其中，γ为核函数参数。

相对于ELM模型，采用KELM模型的好处是不需要明确h(x)的特征映射类型，因此不需要给定隐含层节点的个数 L，使得模型训练的特征空间维数大大降低，从而降低KELM训练的复杂度；另外，与传统支持向量机方法相比，KELM在求解时约束更少，因而性能更好[14]。

5 基于改进果蝇优化算法的模型参数优化

5.1 不确定模型参数分析

在构建基于核极限学习机的预测模型过程中，存在4个不确定模型参数，分别为：相空间重构中的嵌入维数m和延迟时间τ，KELM模型中的正则化参数C和核函数参数γ。4个模型参数的准确赋值在一定程度上决定了KELM模型的预测精度，图6(a)给出了不同的m和τ下模型的预测误差，评价指标采用预测结果与实际结果的均方根误差（root mean square error, RMSE），图6(b)给出了不同的C和γ下模型的RMSE评价指标，所采用的测试数据集为图2中的第12个不变曲线矩特征向量数据序列。

由图6可以看到，不同的模型参数值会造成模型预测性能的差异；在建模过程中，如果设置的参数准确，可以得到较好的预测效果，但是如果给定的参数偏差较大，那么势必会降低模型的预测性能。对此，采用改进的果蝇优化算法实现建模过程中不确定模型参数的优化选择。

5.2 改进果蝇优化算法（IFOA）

5.2.1 果蝇优化算法(FOA) 果蝇优化算法是Pan[16]提出的一种新的群智能优化算法，通过模拟果蝇群体的觅食行为，实现全局最优解的搜索；与传统的遗传算法、蚁群算法和粒子群优化算法相比，该算法具有计算过程简单、编码实现容易和易于理解等优点，且受主观设定参数的影响较小。基于FOA的模型参数优化的实现步骤如下。

（1）参数初始化。初始生成4个果蝇群体，分别指派给m、τ、C和γ这4个待优化参数，设定每个果蝇群体的位置区间[pos_low, pos_up]，设置最大迭代次数（maxgen）和果蝇种群规模（sizepop）。对于每个果蝇群体，在位置区间内随机给定每个果蝇的初始位置X_axisi和Y_axisi如下

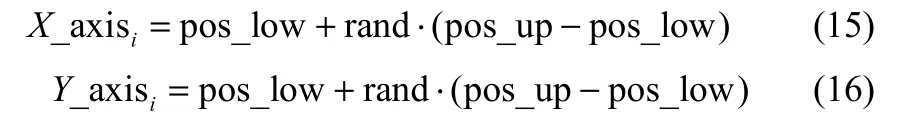
其中，i=1, 2,…, sizepop。

（2）每个果蝇群体中果蝇个体利用嗅觉搜寻食物，随机给定每个个体的飞行方向和距离

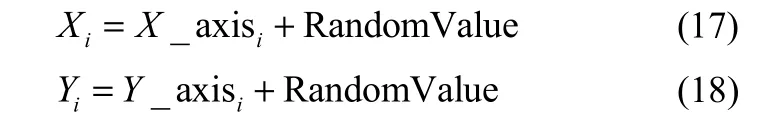
其中，Xi和Yi表示第i个果蝇移动后的位置坐标，RandomValue为搜寻距离。

（3）由于无法知道食物的具体位置，首先估计果蝇个体与原点的距离（Disti），然后计算味道浓度判定值（Si），这个值为距离的倒数

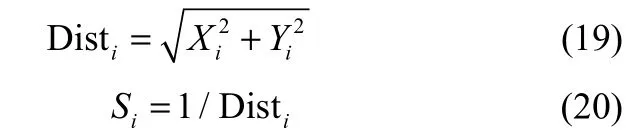
（4）将4个果蝇群体中每个果蝇个体的味道浓度判定值Si（分别对应4个优化参数）代入相空间重构和KELM模型中，得到模型预测输出值，计算预测值与实际值的RMSE指标值，将其作为适应度函数值（Smell），计算每个果蝇个体的Smelli值。

（5）找到果蝇群体中具有最小适应度函数值的个体，如下

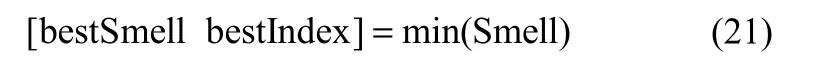
其中，bestSmell表示最小的适应度函数值，bestIndex表示最小适应度函数值对应的果蝇个体的序号。

（6）将具有最小Smelli值的个体标记为最优的果蝇个体，果蝇群体中其他的个体都利用视觉飞向此位置

其中，Smellbest为记录最优适应度函数值的参数。

（7）重复步骤（2）～步骤（5），每一次迭代都判断味道浓度是否比前一代更优，如果是，执行步骤（6），否则继续迭代直至达到最大迭代次数。

根据经典的果蝇优化算法，当在迭代过程中确定最优个体后，其他的个体都向其移动，通过不断缩小搜索范围逐渐接近食物源（最优解），但是如果该个体是局部最优值，则会造成算法陷入局部最优解导致“早熟”问题[17]。对此，对经典的果蝇优化算法进行改进，提出一种改进的果蝇优化算法（IFOA）。

5.2.2 改进果蝇优化算法（IFOA） 为了防止搜索过程过早陷入局部最优解的问题，所提出的 IFOA方法采用全局群体多样进化和局部个体随机变异的策略。

（1）全局群体多样进化策略

根据式(17)、式(18)、式(23)和式(24)，当在迭代过程中确定最优个体（[X_axis, Y_axis]）后，其他个体都会向其移动，那么搜索方向由其信息所决定，极易陷入局部最优解。对此，IFOA中对每个个体的移动方式进行改进，不仅采用当前最优个体的信息，还同时考虑次优个体的信息，即

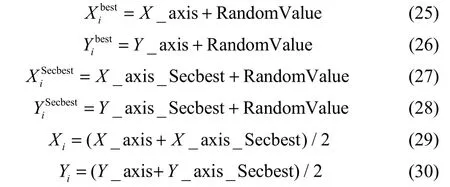
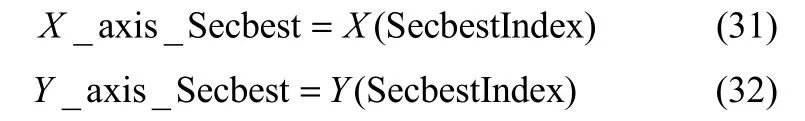
其中，SecbestIndex为当前代中具有第二小 Smell值的个体的序号。

新的群体移动机制中，以每一次迭代中最优和次优的两个个体的信息为导向，可以在一定意义上增大最优解的搜索空间和进化方向，从而增加可行解群体的多样性。

（2）局部个体随机变异策略

根据步骤（1）～步骤（3），首先给定果蝇群体的初始位置，然后每个果蝇个体向不同的方向进行移动，通过计算果蝇个体与原点的距离得到味道浓度判定值，最后确定最优个体。由于果蝇群体的初始位置是随机给定的，那么最优解迭代进化的过程就会受到初始值的影响；如果给定的初始值合适，则能尽快找到最优解，否则极易陷入局部最优值。对此，IFOA方法借鉴模拟退火算法[18]中的以一定概率接受坏解的策略，能够在一定意义上跳出当前最优解，避免过早陷入“早熟”的问题。

根据式(19)和式(20)，最优个体的选择标准为果蝇个体与原点的距离Dist最小（即味道浓度判定值S最大），可以设定一个阈值ξ，当最优个体在连续两代内的位置变化差(Distbest为最优个体与原点的距离，t为迭代的代数)时，以一个较小的概率p（p∈[0,0.5)）放弃该个体，然后在解空间内的任意位置随机生成一个新的个体。ξ的定义如下

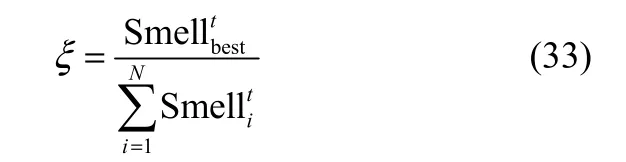
5.2.3 仿真实验 为了验证所提出IFOA方法的有效性，采用Mackey-Glass混沌时间序列进行仿真实验。该时间序列由如下微分方程描述

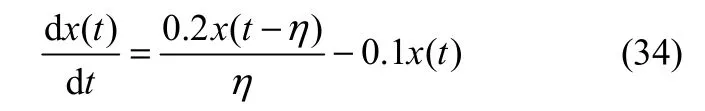
当η＞17时，式(34)具有混沌行为，η越大混沌特征越明显。本文选定 η=30，给定初始值x(t)|t=0=0.9，生成600组数据，其中前400组数据作为训练样本用以建立预测模型，后200组数据作为测试样本。为了说明本文所提出方法的有效性，首先将其与最小二乘支持向量机（least squares support vector machine, LSSVM）方法进行横向对比，LSSVM 被广泛应用于时间序列预测领域，与粒子群算法（particle swarm optimization, PSO）、遗传算法（genetic algorithm, GA）、蚁群算法（ant colony optimization, ACO）和声搜索算法（harmony search, HS）等相结合进行参数的优化选择是其中一个研究热点[19]。将本文所提出的 IFOA-KELM 方法与PSO-LSSVM方法、GA-LSSVM方法、ACO-LSSVM方法和HS-LSSVM方法进行对比，为了更好地体现本文所提出方法的有效性，在对比分析中使PSO、GA、ACO和HS算法不依赖主观设定参数值，将其中各参数设定取值范围，其中：PSO中的惯性权重ω∈[1,3]，学习因子c1∈[0,2]和c2∈[0,2]；GA中的编码串长为10，交叉概率pc∈[0.4,0.8]，变异概率pm∈[0.001,0.005]；ACO中的信息素重要程度因子α=1，转移概率判断因子p0∈[0.1,0.5]、信息素蒸发系数 P∈[0.1,0.5]和信息素增加强度系数 Q∈[0.1,0.5]；HS中和声记忆库的和声数M∈[10,40]，和声记忆库保留概率 HMCR∈[0.5,0.9]，记忆扰动概率 PAR∈[0.05,0.2]，带宽范围为[0.001,1]。设定算法迭代次数为100次，每个预测模型重复执行20次取平均结果（平均值±标准偏差），每次执行过程中，各算法的相关参数在取值范围内随机取值，由RMSE和MAE（mean absolute error）作为评价指标，对比结果见表1。

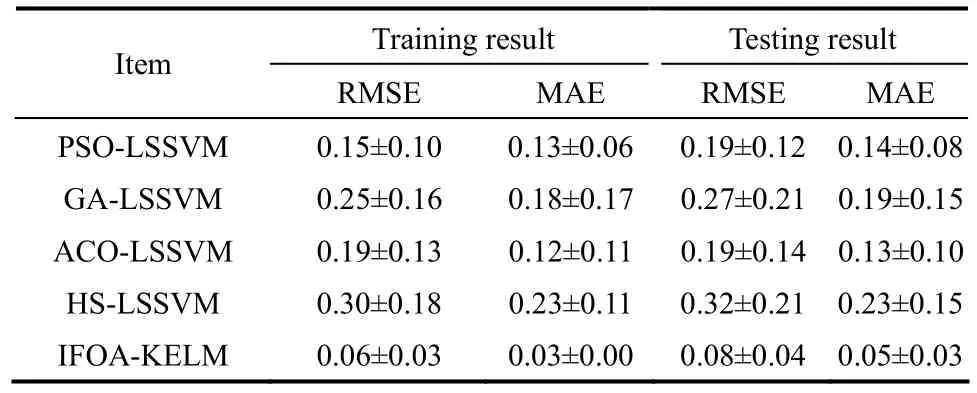
表1 不同方法的MAE和RMSE指标对比（横向）Table 1 Comparison of MAE and RMSE index value of different methods (horizontal comparison)

由表1的结果可以看到，相比于PSO-LSSVM、GA-LSSVM、ACO-LSSVM和HS-LSSVM这几种方法，本文所提出的IFOA-KELM方法在训练集和测试集上都有较好的预测效果。由于不受主观设定参数的影响，多次预测的结果较为稳定，波动较小。

为了进一步说明IFOA-KELM的有效性，将其与 FOA-KELM 方法、IFOA1-KELM 方法[17]、AMFOA-KELM方法[20]进行纵向比较。各种方法的对比结果见表2。

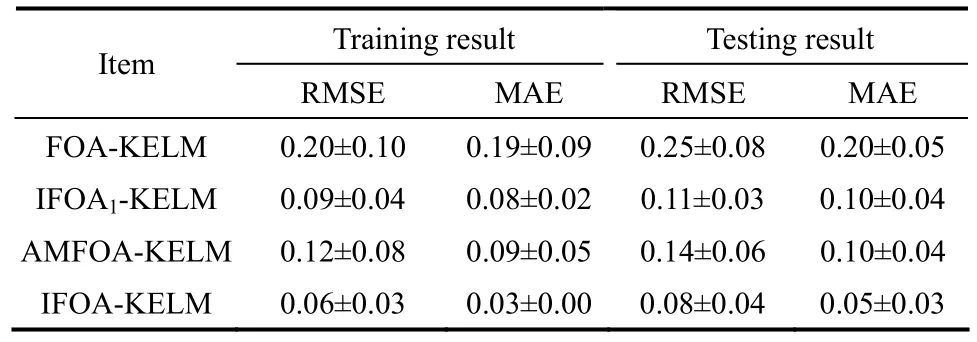
表2 不同方法的MAE和RMSE指标对比（纵向）Table 2 Comparison of MAE and RMSE index value of different methods (vertical comparison)

由表2的对比结果可以看到，IFOA-KELM的预测性能优于其他几种方法。

6 基于物元分析理论的工况预测

物元分析理论是蔡文等[21]所建立可拓学的重要组成部分，综合考虑定性分析和定量分析两个方面，由信息的可拓展性去解决问题。首先建立所预测28个不变曲线矩特征向量的物元模型如下

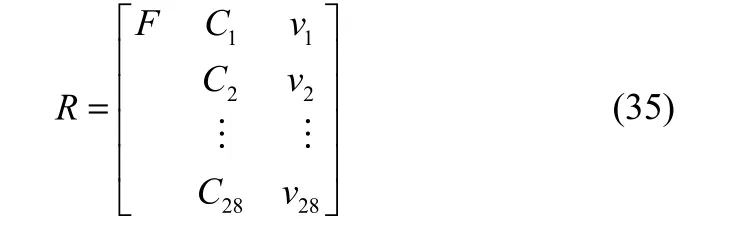
式中，C为不变曲线矩特征；v为不变曲线矩特征的取值。

在油田生产中，抽油机常出现的故障类型有如下11种：“正常”（为了便于研究，将“正常”看作一种故障类型）、“气体影响”、“供液不足”、“抽油杆断落”、“油稠”、“游动阀漏失”、“固定阀漏失”、“泵上碰”、“泵下碰”、“油井出砂”和“柱塞脱出工作筒”，然后由已有的示功图样本建立每一种故障类型的不变曲线矩特征值库[1]，其物元模型表示如下

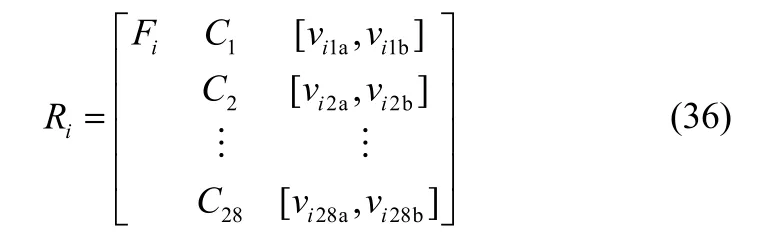
其中，i=1,2,…,11，Fi为第i种故障类型；vi=[via,vib]表示第i种故障类型的不变曲线矩特征的取值区间。

根据式(37)～式(39)计算所预测样本与各故障类型的关联度

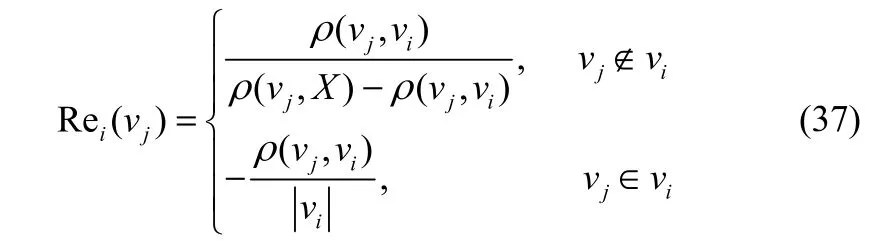
其中，j=1, 2, …, 28；vj为第Cj个不变曲线矩特征的取值，Rei(vj)为第Cj个不变曲线矩特征下所预测样本与第i种故障类型的关联函数；“ vj∉ vi”表示所预测样本的第 Cj个不变曲线矩特征的取值不在区间vi=[via,vib]内，“vj∈vi”表示在区间内；X为节域，本文取X=[0,20]；|vi|为区间的间距；ρ(vj, vi)表示第 Cj个不变曲线矩特征的值与区间[via,vib]的距离，定义如下

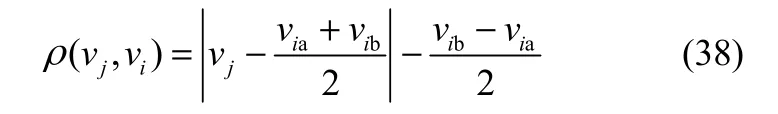
那么，所预测样本与第i种故障类型的关联度定义如下

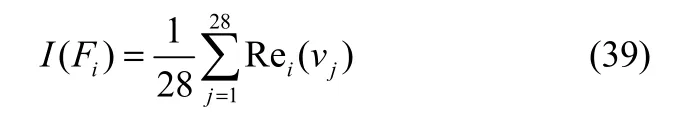
采用最大值原则，最大值发生程度所对应的故障类型即为所预测样本的故障类型；若所有的I(Fi)＜0，则认为所预测样本不属于当前任一故障类型。

7 实例验证

采用国内某油田作业区的两口抽油井进行实例验证，“油井1”的主要生产参数：额定电压380 V、额定功率37 kW、电动机额定转速980 r·min−1、冲次3次·min−1、冲程2.5 m；“油井2”的主要生产参数：额定电压380 V、额定功率27 kW、电动机额定转速490 r·min−1、冲次4次·min−1、冲程 3.5 m。以“小时”为采样时间间隔，采集每口油井在连续250 h生产时间内的250幅示功图，采集设备如图7所示。

图7 示功图采集设备Fig.7 Data acquisition equipment of dynamometer card

为了验证所提出方法的有效性，首先进行如下仿真实验，250幅示功图中选取前240幅作为训练样本建立预测模型，后10幅作为测试样本，由生产技术人员人工识别测试样本的故障类型，作为预测准确率的评价标准。将本文所提出的IFOA-KELM-MEA 预 测 模 型 分 别 与PSO-LSSVM-MEA 、 GA-LSSVM-MEA 、ACO-LSSVM-MEA 、 HS-LSSVM-MEA 、IFOA1-KELM-MEA和AMFOA-KELM-MEA预测模型进行对比，PSO、GA、ACO和HS算法的主观设定参数值采用5.2.3节的取值范围，在预测每个样本时，预测模型重复执行20次得到预测准确率，每次执行过程中，各算法的相关参数在取值范围内随机取值。各预测模型的预测准确率如图8所示。

由图8可以看到，由于受到主观设定参数不确定性的影响，PSO、GA、ACO和HS算法的参数优化稳定性较差，使得 PSO-LSSVM-MEA、 GA-LSSVM-MEA 、 ACO-LSSVM-MEA 和HS-LSSVM-MEA模型的预测准确率的波动较大，在70%～100%之间波动，预测效果不是很理想；而IFOA1-KELM-MEA、AMFOA-KELM-MEA 和IFOA-KELM-MEA模型中的优化算法不需要设定主观参数，因此受其值的影响较小，使得预测结果稳定性较好，预测准确率保持在95%～100%。

图8 各模型预测准确率对比Fig.8 Comparisons of prediction accuracy of different models

图 8反映出 IFOA1-KELM-MEA、AMFOAKELM-MEA和IFOA-KELM-MEA模型的预测效果较好，为了说明本文所提出IFOA-KELM-MEA模型有更好的性能，进行如下仿真实验，将两口油井的250幅示功图都作为训练样本，预测下一个时间点的示功图故障类型，然后与实际采集的示功图（图9）进行对比。

根据人工分析结论，图9(a)示功图反映抽油杆接箍与油管偏磨严重，造成上死点处的负荷突然增大，典型的“泵上碰”故障类型；图9(b)示功图反映图形右下角严重缺失，加载线正常，但是卸载线变化缓慢，典型的“供液不足”故障类型。IFOA1-KELM-MEA、AMFOA-KELM-MEA和IFOA-KELMMEA模型的预测结果见表3。

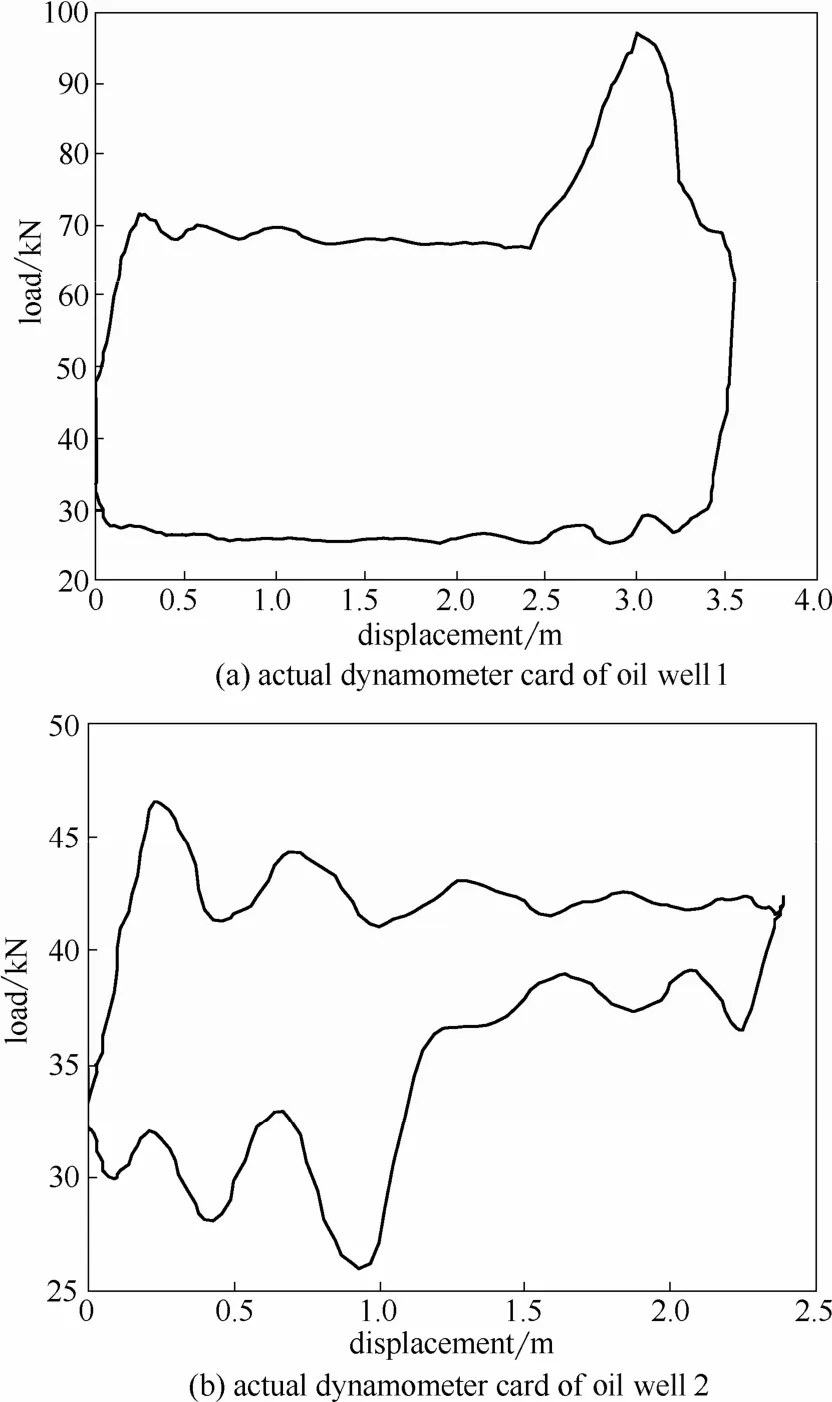
图9 两口油井采集的实际示功图Fig.9 Actual dynamometer cards of two oil wells

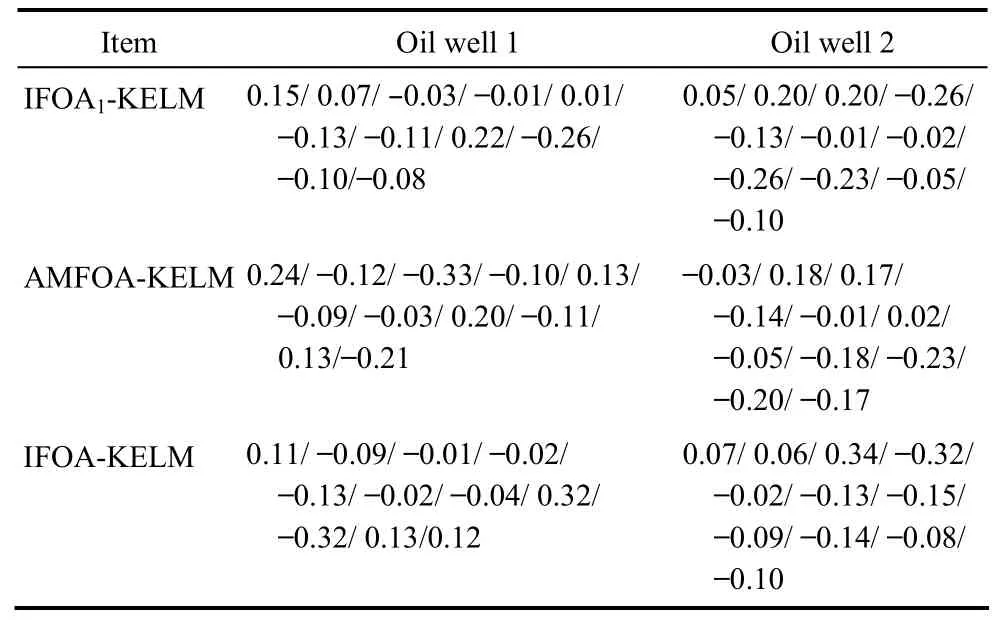
表3 3个模型的关联度对比（I(F1)/ I(F2)/ I(F3)/ I(F4)/ I(F5)/ I(F6)/ I(F7)/ I(F8)/ I(F9)/ I(F10)/ I(F11)）Table 3 Comparison of correlation degree (I(F1)/ I(F2)/ I(F3)/ I(F4)/ I(F5)/ I(F6)/ I(F7)/ I(F8)/ I(F9)/ I(F10)/ I(F11)) among three models

根据表3的对比结果可以看到，对于“油井1”故障类型的预测，AMFOA-KELM-MEA模型的结论是 I(F1)最大，认为属于“正常”，与实际工况不符，IFOA1-KELM-MEA和IFOA-KELM-MEA模型都得到了I(F8)最大的结论，都认为属于“泵上碰”，但是IFOA1-KELM-MEA模型得到的与“泵上碰”的关联度明显小于本文所提出的IFOA-KELM-MEA模型，说明后者的结论更精确，这也正是采用物元分析理论的优势，不止评价“属于”或“不属于”，还能得到“属于”或“不属于”的程度；对于“油井 2”故障类型的预测，IFOA1-KELM-MEA模型得到的结论是I(F2)和I(F3)同为最大，无法分辨是属于“气体影响”还是“供液不足”故障类型，AMFOA-KELM-MEA模型的结论是 I(F2)最大，认为属于“气体影响”，与实际工况不符，而本文所提出的IFOA-KELM-MEA模型得到的I(F3)结果明显大于其他类型，预测结果明确，性能优于其他两个预测模型。

8 结 论

针对游梁式抽油机采油系统井下工况的预测问题，首先将28个不变曲线矩特征向量作为预测序列变量，通过0-1混沌测试法验证其混沌特性后证明可以采用基于混沌时间序列的预测方法。然后根据核极限学习机理论建立预测模型，将相空间重构后的Xi和Yi分别作为其输入和输出；经过仿真实验，预测模型中的嵌入维数 m、延迟时间 τ、正则化参数C和核函数参数γ会影响预测精度，对此采用改进的果蝇优化算法进行参数的寻优；通过横向和纵向不同方法的比较，验证了改进算法中所采用全局群体多样进化和局部个体随机变异策略的有效性。对于所得到的预测变量的工况类型诊断，由可拓理论中的物元分析方法计算其与各标准工况的关联度，通过某油田作业区两口抽油井的实际生产数据验证了预测结果与实际工况的一致性。

[1]李琨, 高宪文, 仇治学, 等. 有杆泵抽油系统井下工况诊断的物元分析方法[J]. 东北大学学报（自然科学版）, 2013, 34(5): 613-617. LI K, GAO X W, QIU Z X, et al. Matter-element analysis method of downhole conditions diagnosis for suck rod pumping system [J]. Journal of Northeastern University (Natural Science), 2013, 34(5): 613-617.

[2]LI K, GAO X W, ZHOU H B, et al. Fault diagnosis for down-hole conditions of sucker rod pumping systems based on the FBH-SC method [J]. Petroleum Science, 2015, 12(1): 135-147.

[3]REGES G D, SCHNITMAN L, REIS R, et al. A new approach to diagnosis of sucker rod pump systems by analyzing segments ofdownhole dynamometer cards [C]// SPE Artificial Lift Conference—Latin America and Caribbean, Salvador Bahia, Brazil: Society of Petroleum Engineers, 2015: SPE-173964-MS: 1-13.

[4]梁华. 有杆抽油系统故障递阶诊断的故障识别研究[J]. 西南石油大学学报(自然科学版), 2015, 37(1): 165-171. LIANG H. Hierarchical fault diagnosis of rod pumping system based on fault distinguishing [J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 165-171.

[5]任伟建, 赵月娇, 王天任, 等. 基于生物地理优化算法的抽油机故障诊断研究[J]. 系统仿真学报, 2014, 26(6): 1243-1250, 1273. REN W J, ZHAO Y J, WANG T R, et al. Research on pump-jack fault diagnosis method based on biogeography-based optimization algorithm [J]. Journal of System Simulation, 2014, 26(6): 1243-1250, 1273.

[6]LI K, GAO X W, TIAN Z D, et al. Using the curve moment and the PSO-SVM method to diagnose downhole conditions of a sucker rod pumping unit [J]. Petroleum Science, 2013, 10(1): 73-80.

[7]LI K, GAO X W, YANG W, et al. Multiple fault diagnosis of down-hole conditions of sucker-rod pumping wells based on Freeman chain code and DCA [J]. Petroleum Science, 2013, 10(3): 347-360.

[8]GOTTWALD G A, MELBOURNE I. On the implementation of the 0-1 test for chaos [J]. SIAM Journal on Applied Dynamical Systems, 2009, 8(1): 129-145.

[9]田中大, 李树江, 王艳红, 等. 短期风速时间序列混沌特性分析及预测[J]. 物理学报, 2015, 64(3): 030506-1-12. TIAN Z D, LI S J, WANG Y H, et al. Chaotic characteristics analysis and prediction for short-term wind speed time series [J]. Acta Phys. Sin., 2015, 64(3): 030506-1-12.

[10]GOTTWALD G A, MELBOURNE I. On the validity of the 0-1 test for chaos [J]. Nonlinearity, 2009, 22(6): 1367-1382.

[11]周伟, 李引珍, 俞建宁. 利用0-1测试快速识别交通流时间序列中的混沌[J]. 系统工程, 2015, 33(9): 122-126. ZHOU W, LI Y Z, YU J N. Fast identification for chaos of traffic flow times series based on 0-1 test [J]. Systems Engineering, 2015, 33(9): 122-126.

[12]HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications [J]. Neurocomputing, 2006, 70(1): 489-501.

[13]王新迎, 韩敏. 多元混沌时间序列的多核极端学习机建模预测[J].物理学报, 2015, 64(7): 070504-1-7. WANG X Y, HAN M. Multivariate chaotic time series prediction using multiple kernel extreme learning machine [J]. Acta Phys. Sin., 2015, 64(7): 070504-1-7.

[14]韩敏, 刘晓欣. 一种基于互信息变量选择的极端学习机算法[J].控制与决策, 2014, 29(9): 1576-1580. HAN M, LIU X X. An extreme learning machine algorithm based on mutual information variable selection [J]. Control and Decision, 2014, 29(9): 1576-1580.

[15]HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 513-529.

[16]PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example [J]. Knowledge-Based Systems, 2012, 26: 69-74.

[17]WANG L, SHI Y L, LIU S. An improved fruit fly optimization algorithm and its application to joint replenishment problems [J]. Expert Systems with Applications, 2015, 42(9): 4310-4323.

[18]KIRKPATRICK S. Optimization by simulated annealing [J]. Science, 1983, 220(5): 671-679.

[19]李琨, 韩莹, 黄海礁. 基于IBH-LSSVM的混沌时间序列预测及其在抽油井动液面短期预测中的应用[J]. 信息与控制, 2016, 45(2): 241-247. LI K, HAN Y, HUANG H J. Chaotic time series prediction based on IBH-LSSVM and its application for short-term prediction of dynamic fluid level of the oil wells [J]. Information and control, 2016, 45(2): 241-247.

[20]WANG W C, LIU X G. Melt index prediction by least squares support vector machines with an adaptive mutation fruit fly optimization algorithm [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 141: 79-87.

[21]蔡文, 杨春燕, 林伟初. 可拓工程方法[M]. 北京: 科学出版社, 2000: 18-97. CAI W, YANG C Y, LIN W C. Extension Engineering Method [M]. Beijing: Science Press, 2000: 18-97.

IFOA-KELM-MEA model based transient prediction on down-hole working conditions of beam pumping units

LI Kun1, HAN Ying1, SHE Dongsheng1, WEI Zefei1, HUANG Haijiao2
(1College of Engineering, Bohai University, Jinzhou 121013, Liaoning, China;2The Fifth District of Jinzhou Oil Production Plant, Liaohe Oilfield Company, Jinzhou 121209, Liaoning, China)

Prediction for down-hole working conditions of beam pumping units is an effective strategy to timely control oil well's working state, and is important to improve production efficiency and to reduce maintenance cost. Chaos theory was used in transient prediction for oil well's down-hole working conditions. First, moment eigenvalues of invariant curves were extracted from dynamometer chart as predictive variables. Then, after data sequence of these predictive variables were proved to have chaotic characteristics, chaotic time series prediction model was established by ELM (kernel extreme learning machine) method and several uncertain variables of the model were optimally solved by IFOA (improved fruit fly optimization algorithm) with two strategies of global population diversity-evolution and local individual random-variation. Finally, model predictive results were analyzed to determine fault types according to MEA (matter-element analysis) method. Case study of two oil wells in one oilfield showed that the IFOA-KELM-MEA prediction model was reasonable and effective.

chaotic time series prediction; beam pumping units; kernel extreme learning machine; fruit fly optimization algorithm; matter-element analysis; measurement; petroleum; model

LI Kun, bhulikun@163.com

TP 273

：A

：0438—1157（2017）01—0188—11

10.11949/j.issn.0438-1157.20160834

2016-06-20收到初稿，2016-09-28收到修改稿。

联系人及第一作者：李琨（1983—），男，博士，副教授。

国家自然科学基金项目（61403040）。

Received date: 2016-06-20.

Foundation item: supported by the National Natural Science Foundation of China (61403040).