基于模型分块逼近的三关节机器人鲁棒滑模控制

马莉丽, 钟 斌

(中国人民武装警察部队工程大学 装备工程学院,陕西 西安 710086)



基于模型分块逼近的三关节机器人鲁棒滑模控制

马莉丽, 钟 斌

(中国人民武装警察部队工程大学 装备工程学院,陕西 西安 710086)

三关节机器人结构参数、作业环境的外界干扰及结构振动等不确定因素均会造成其动力学模型不确定,导致机器人关节位置镇定或轨迹跟踪控制器的设计具有一定的难度。为此,设计三个RBF(Radical Basis Function)神经网络分别对机器人不确定模型中的三个不确定项进行分块逼近,得到三个不确定项的估计信息,从而得出机器人估计模型,神经网络的权值采用适应算法。针对机器人估计模型设计鲁棒滑模控制律,其中鲁棒项用于克服神经网络建模误差。通过定义Lyapunov函数,证明了控制系统是稳定的。实验结果也表明了三关节均约在1s时达到期望位置或跟踪期望轨迹,位置镇定误差或轨迹跟踪误差也快速、稳定地趋于零。

三关节机器人; 模型分块逼近; 关节控制; RBF神经网络

三关节机器人(以下简称机器人)结构紧凑，所占空间小，灵活性强，工作空间较大，避障性好，广泛应用于工业机器人中。对机器人控制问题的研究一般集中于对其关节的位置控制，或者使每个关节能够按照期望的动态品质跟踪期望轨迹，或者使每个关节渐近稳定于指定的某个位置，即其控制问题归纳为轨迹跟踪或位置镇定两类[1-5]。然而，机器人本身结构参数的变化或工作环境中的干扰往往导致机器人动力学模型的不确定，这就给控制器的设计带来了较大的难度[6-8]。通常针对这类问题采用的控制方法有滑模控制[9-11]、自适应控制、模糊控制[12]和鲁棒控制[13]。其中，滑模控制无需精确的动力学模型和专门的多变量解耦，只需根据轨迹跟踪或位置镇定误差合理设计滑模面，具有快速响应、无超调及鲁棒性强等优点，成为不确定机器人系统控制的首选方法。但该方法易导致控制器的输出幅值波动较大，所以滑模控制通常与其他控制方法相结合使用，才能得到较满意的控制效果，如文献[11]和文献[12]。与这些文献研究方法不同的是，本文采用了三个RBF神经网络分别对不确定机器人模型中三个不确定项进行建模，即采用分块逼近的方法得到其估计信息，神经网络的权值采用自适应算法。已有研究表明，RBF神经网络能以任意精度逼近任意非线性函数[14]。针对机器人估计模型，设计误差滑模函数和PI控制项及用于克服神经网络建模误差的鲁棒项，即构成机器人的PI鲁棒滑模控制。利用Lyapunov稳定性理论证明了所设计的控制系统是全局渐近稳定的。实验结果也表明三关节均能达到稳定、快速的轨迹跟踪和位置镇定的控制要求。

1 三关节机器人动力学模型及问题的提出

三关节机器人结构示意图如图1所示。后臂质量为m2,前臂质量为m3,后臂长为l2,前臂长为l3,后臂质心到关节2的距离为r2,前臂质心到关节3的距离为r3,q1、q2和q3分别为关节1、关节2和关节3的转角,立柱转动惯量为I1,后臂转动惯量为I2,前臂转动惯量为I3,不计关节摩擦力矩。

图1 三关节机器人Fig.1 Robot with three joints

三关节机器人动力学模型为:

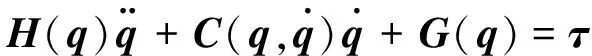
(1)

h11=I1+a1cos2(q2)+a2cos2(q2+a3)+ 2a3cos(q2)cos(q2+q3)

h12=h21=h13=h31=0

h22=I2+a1+a2+2a3cos(q3)

h23=h32=a2+a3cos(q3)

h33=I3+a2

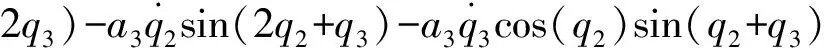
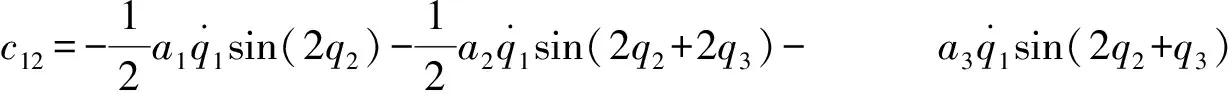
c21=-c12

c31=-c13

c33=0

g1=0

g2=b1cos(q2)+b2cos(q2+q3)

g3=b2cos(q2+q3)

(2)

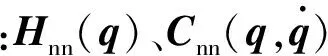
现定义滑模函数:

(3)

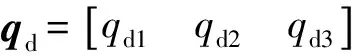
于是,有:

(4)

(5)

将式(2)代入式(5),得:

(6)

2 RBF神经网络算法及PI鲁棒滑模控制律设计

以神经网络对H(q)的建模为例,RBF神经网络算法为:

(7)

式中:m为神经网络神经元个数;ΞH(e)=[ξH1(e),ξH2(e),…,ξHm(e)]为隐含层高斯基函数的输出;xk=[xk1,xk2,…,xk(2m)]为第k个神经元的中心向量;y=[y1,y2,…,ym]T为高斯基函数的基宽向量;WH=[WH1,WH2,…,WHm]为输出层权值。

同理,有:

(8)

(9)

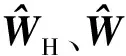
(10)

式中:ΓH、ΓC和ΓG均为对称正定矩阵。

(11)

式中:KP和KI分别为比例系数和积分系数,且KP>0、KI>0;τm为基于模型估计的控制律,且

(12)

其中,τr为用于克服神经网络建模误差的鲁棒项,且

τr=Krsgn(s)

(13)

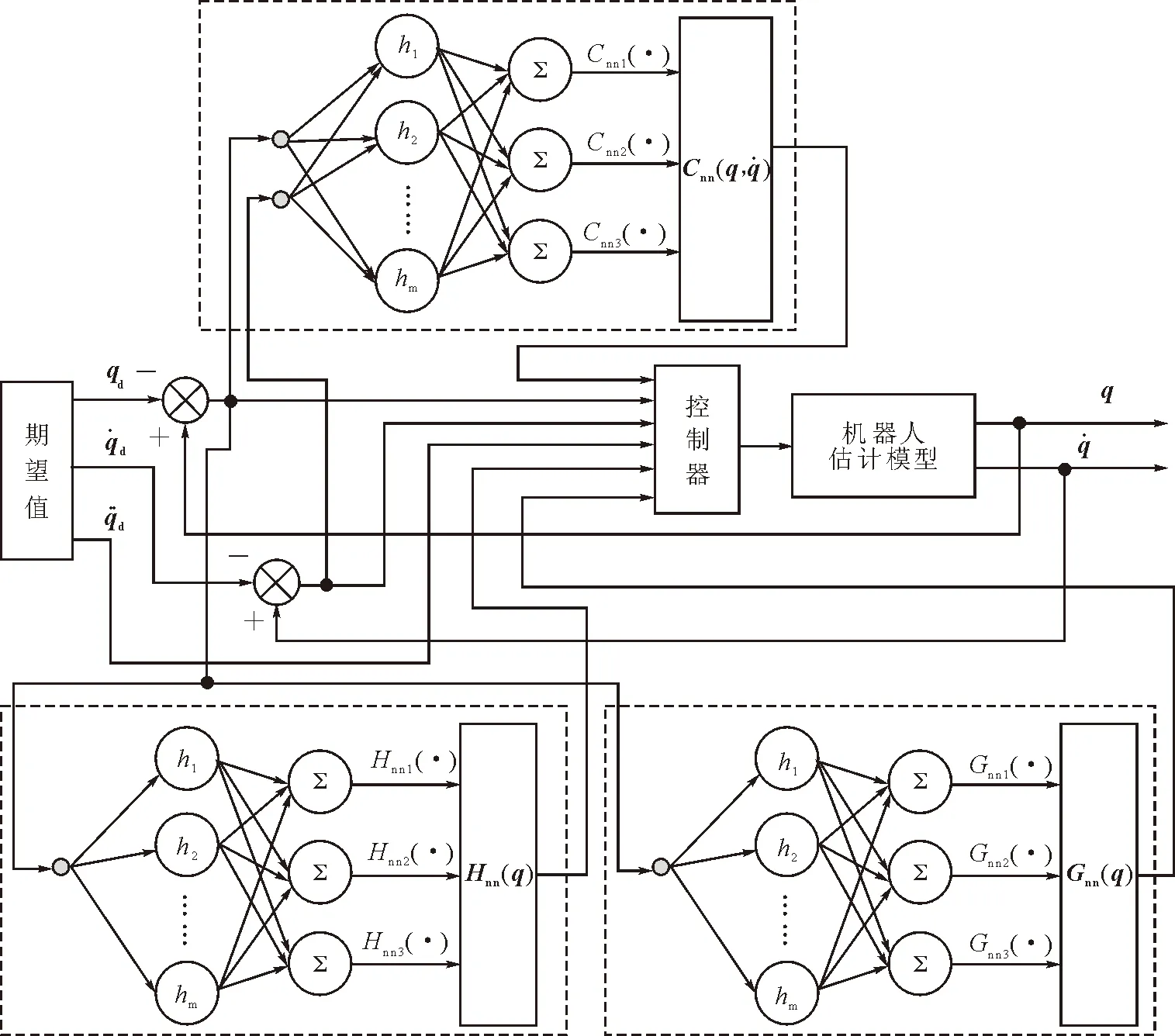
图2 控制系统结构框图Fig.2 Control system’s structure

3 控制系统稳定性分析

为分析控制系统的稳定性,现定义基于积分型的Lyapunov函数:

(14)

显然,V是正定的,现对V求一阶导数,有:

(15)

(16)

由式(1)、式(4)和式(8),得:

(17)

再由式(9)、式(11)～式(13),得:

(18)

于是,由式(17)和式(18),得:

(19)

将式(19)代入式(16),得:

(20)

由于:

(21)

同理:

(22)

将式(21)和式(22)代入式(20),得:

(23)

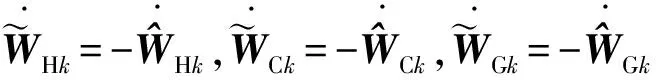
(24)

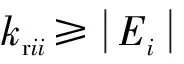
(25)

4 实验验证

机器人参数:m2=30 kg,m3=26 kg;r2=0.6 m,r3=0.5 m;I1=3.61 (kg·m2),I2=2.35 (kg·m2),I3=1.95 (kg·m2)。

关节初始值:

三关节位置镇定期望指令:

轨迹跟踪期望指令:

RBF神经网络的神经元个数m=5,高斯基函数基宽为3。控制器参数:KP=KI=100×I,Λ=5×I。

三关节的位置镇定结果如图3所示。从图中可以看出,三关节约在1 s时达到并稳定在期望位置,也能在1 s时跟踪期望轨迹,实验还表明三关节也能在1 s时跟踪期望速度。轨迹跟踪结果如图4所示。为了验证本文控制方法的有效性和优势,与文献[14]所采用的RBF神经网络滑模控制方法进行了对比实验,限于篇幅,仅给出了如图5所示的关节位置镇定控制结果。通过对比图3和图5可以看出,采用文献[14]的控制方法时,三个关节约在4 s时才能达到并稳定在期望位置。

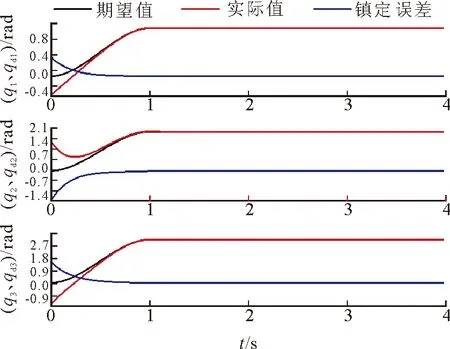
图3 采用本文控制方法的关节位置镇定结果Fig.3 Control of position stabilizing with method of this paper

图4 采用本文控制方法的关节轨迹跟踪结果Fig.4 Control of trajectory tracking with method of this paper

图5 采用文献[14]的控制方法时关节位置镇定结果Fig.5 Control of position stabilizing with control method of reference [14]

5 结 论

为了解决三关节机器人不确定动力学模型的关节位置镇定或轨迹跟踪控制器设计较困难的问题，通过设计三个RBF神经网络，分别对机器人不确定模型中的三个不确定项进行分块逼近，得到机器人估计模型。针对机器人的估计模型设计了鲁棒滑模控制律，通过本文的研究得出了以下主要结论：

1) 通过定义Lyapunov函数,证明了控制系统是全局渐近稳定的;

2) 仿真实验表明,三关节机器人的各关节均约在1 s时达到期望位置或跟踪期望轨迹,其位置镇定误差或轨迹跟踪误差也约在1 s时渐近地趋于零。

[1] 季晔, 刘宏昭, 原大宁, 等. 并联机构位置正解方法研究 [J]. 西安理工大学学报, 2010, 26(3): 277-282. JI Ye, LIU Hongzhao, YUAN Daning. Research on approach of forward positional analysis of parallel manipulator [J]. Journal of Xi’an University of Technology, 2010, 26(3): 277-282.

[2] HARMON F G, FRANK A A, JOSHI S S. The control of a parallel hybrid-electric propulsion system for a small unmanned aerial vehicle using a CMAC neural network [J]. Neural Networks, 2012, 18(5): 772 -780.

[3] ODA M. Space robot experiments on NASDA’S ETSVII satellite: preliminary overview of the experiment results [C]∥IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2011: 1390-1395.

[4] 赵涛, 刘明雍, 周良荣. 基于Lyapunov方法的轮式移动机器人全局轨迹跟踪控制 [J]. 火力与指挥控制, 2010, 35(7): 87-89. ZHAO Tao, LIU Mingyong, ZHOU Liangrong. Lyapunov based global trajectory tracking control for wheeled mobile robot [J]. Fire Contorl & Command Control, 2010, 35(7): 87-89.

[5] 赵涛, 刘明雍, 周良荣. 移动机器人的轨迹跟踪控制新方法 [J]. 火力与指挥控制, 2010, 35(11): 33-34, 46. ZHAO Tao, LIU Mingyong, ZHOU Liangrong. Novel method for trajectory tracking control of mobile robot [J]. Fire Contorl & Command Control, 2010, 35(11): 33-34, 46.

[6] LI Z J, ZHANG Y N, YANG Y P. Support vector machine optimal control for mobile wheeled inverted pendulums with unmodeled dynamics [J]. Neurocomputing, 2011, 13(73): 2773-2782.

[7] BANERJEE A, BHATTACHARYA B, MALLIK A K. Large deformation of cantilever beams with geometric non-linearity: analytical and numerical approaches [J]. International Journal of Non-linear Mechanics, 2010, 43(5): 366-376.

[8] 田慧慧, 苏玉鑫. 机器人系统输出反馈重复学习轨迹跟踪控制 [J]. 控制与决策, 2012, 27(11): 1756 -1760. TIAN Huihui, SU Yuxin. Global asymptotic stable repetitive output feedback tracking control of robot manipulators [J]. Control and Decision, 2012, 27(11): 1756-1760.

[9] UTKIN V I. Sliding mode control design principles and applications to electric drives [J]. IEEE Trans and Electron, 2010, 40(1): 23-26.

[10] LI T, HSENG S, HUANG Y C. MIMO adaptive fuzzy terminal sliding-mode controller for robotic manipulators [J]. Information Sciences, 2010, 180(6): 4641-4660.

[11] DELAVARI H, GHADERI R, RANJBAR A, et al. Fuzzy fractional order sliding mode controller for nonlinear systems [J]. Commun in Nonlinear Sci Numer and Simulat, 2010, 15(4): 963-978.

[12] 胡盛斌, 陆敏恂. 多个关节机器人反馈线性化双模糊滑模控制 [J]. 机械科学与技术, 2013, 32(1): 105-110. HU Shengbin, LU Minxun. Feedback linearization double fuzzy sliding mode control for multi-links robot [J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(1): 105-110, 115.

[13] ISLAM S, LIU P X. Robust adaptive fuzzy output feedback control system for robot manipulators [J]. IEEE/ASME Trans on Mechatronics, 2011, 16(2): 288-296.

[14] 邵克勇, 马千惠, 邹运, 等. 基于径向基函数神经网络的多关节机器人滑模控制器 [J]. 计算机测量与控制, 2014, 22(5): 1385-1387. SHAO Keyong, MA Qianhui, ZOU Yun, et al. Sliding mode control for multi-joint robot based on RBF neural network [J]. Computer Measurement & Control, 2014, 22(5): 1385-1387.

(责任编辑 周 蓓)

Research on three-joint robot’s robust sliding mode control based on model’s partitional approximating

MA Lili， ZHONG Bin

(College of Equipment Engineering, Engineering University of Chinese Armed Police Force, Xi’an 710086, China)

Generally, the dynamic model of robot with three-joint is undetermined due to three-joint robot’s uncertain structure parameters, working environment’s external interfere and structural vibration. Accordingly, it is difficult to control the robot’s joints’ position stabilizing and trajectory tracking and controller’s design due to the dynamic model’s uncertainty. Therefore, three designed RBF(Radical Basis Function) neural networks are used to respectively model the three undetermined terms of the undetermined robot dynamic model, with partition approximating the three-joint robot. Three undetermined terms’ estimation information is respectively obtained, with the robot’s estimation model obtained. The neural networks’ weights are obtained through the adaptive algorithm. The robust sliding mode control law is designed based on the robot’s estimation model. The control law’s robust term is used to overcome the neural networks’ modeling error. The control system’s stability is proved by defining Lyapunov function. The simulation experiments test verifies that three joints can trace ideal trajectory and reach an ideal position in 1s, and stabilization error and tracking error can fast and stably approximate to zero.

robot with three-joint; model’s partitional approximating; joints’ control; RBF neural network

10.19322/j.cnki.issn.1006-4710.2016.04.011

2015-09-06

国家自然科学基金资助项目(51005246);中国人民武装警察部队工程大学基础研究基金资助项目(WJY201509)

马莉丽,女,博士,讲师,研究方向为机电系统智能控制及其自动化、机器人控制、军事装备理论及其应用等。E-mail:malilichina@163.com

TP242.2

A

1006-4710(2016)04-0437-06