从随机事件的分析到带灾难的投资策略

农宇轩

（中南大学 数学与统计学院，湖南 长沙，410012）

从随机事件的分析到带灾难的投资策略

农宇轩

（中南大学 数学与统计学院，湖南 长沙，410012）

该文以赌场中流行的骰宝游戏为例，设定在胜负比率乘上赔率所满足的条件下进行无限局游戏时，研究两种不同的投注策略所得到的盈亏情况，结果表明赌户最终都会亏。进而提出一个相比赌博结果确定性较高的投资问题，即在固定的多轮投资中，在已知将要发生的灾难的次数时，在控制风险最小的情况下，怎样投资才能获得最大的收益。分析了在投入与回报相等的情况下，每一轮投资的具体策略以及最终的收入情况。

直觉错误；概率论；带灾难的投资

引言

在没有系统地分析的情况下，人们倾向于用直觉分析问题，但是通过概率论分析，我们可以得出直觉并不可靠的结论。参与赌博的一个重要原因是因为觉得赢面比较大。然而事实并非如此，通过概率论的分析，得到了在赌局中，亏损的概率更大的结论，同时证明了当进行赌博的次数比较多时，不论有多少钱，最终都会输光的结论，可靠的证明了赌博的危害性。

亏损的必然是由于赔率的设置与结果的随机性造成的，本文还考虑了确定性更大的投资的问题，并且分析了存在一些特殊条件（称之为灾难）下的投注策略。

1 随机事件分析

1.1 直觉错误

未来还没有发生的事情，我们并不能明确地确定将会发生的是什么，人们会本能的去估计某件事情发生的可能性的大小，而这种估计往往都是通过直觉来进行的，有时候直觉可能是对的，但也不总是对的，这时候就需要通过数学的方法来进行合理的估计。

人们的直觉不总是那么的可靠，需要通过数学的方式来进行进一步的验证来确定它的可靠性，下面我们将给出一些具体的直觉错误的例子。

1.1.1 生日问题

足球场上有2个球队，每队11个人，1个裁判，总共23人中，至少有2人同一天生日的概率是多少？人们对这一概率的估计都严重偏低了。

用 X[i,j]表示第i个人和第j个人不是同一天生日的概率，不难得到：

令事件A表示n个人都不是同一天生日，有：

1.1.2 三门问题

三门问题起源于一档美国的电视游戏节目，规则如下：

参赛的选手可在三扇门中选一扇，且参赛选手知道两扇门后是山羊，一扇门后汽车，选中车就可将车带走。主持人知道这三扇门后到底是车还是羊，为了给游戏增加一点趣味性，当参赛者选好了一扇门以后，主持人会打开一扇背后是羊的门，并且会询问参赛者是否要改变他现在的选择去选另一扇没有打开的门。

从直觉上来分析，很多人认为换和不换是一样的，用摸球模型来表示时，一个盒子里有三个球，两白一红，先摸出一个白球，那么剩下的两个球不管怎么摸，摸到红球的概率都是

而从数学上分析，“换门”这一策略能获得汽车的概率确实更高，下面我们将列出所有可能的情况：

1）所选门后是羊一，主持人打开羊二的门，换门后获得汽车

2）所选门后是羊二，主持人打开羊一的门，换门后获得汽车

3）所选门后是车，主持人打开一扇背后是羊的门，不换门后获得汽车。

1.2 赌博模型分析

骰宝是赌场内比较火的一种玩法。每次投掷三个骰子，下注的规则与赔率如下：

一、“大”，总点数为11至17(遇围骰庄家通吃)，赔率1∶1；

二、“小”，总点数为4至10(遇围骰庄家通吃)，赔率1∶1；

三、“围骰”，开出三颗点数的骰子，赔率1∶24；

四、“点数”，点数总和，赔率如下：

A．点数为4或者17点，1∶50

B．点数为5或者16点，1∶18

C．点数为6或者15点，1∶14

D．点数为7或者14点，1∶12

E．点数为8或者13点，1∶8

F．点数为9，10或者11，12点，1∶6

首先考虑“大”和“小”的获胜的概率，设三个骰子掷出的数字分别为321,, AAA

其中 Ai=={{1,,22,3,,34,,54,,6},5,6,}i=1,2,3,显然 (P(大)= (P(小),且 (P(大)+ (P（小）= (P（围骰）=1，我们只需要计算“围骰”的情况，即可知道“大”和“小”的情况，而“围骰”共有六种情况，每种情况的概率为：

则：

从而“围骰”的获胜的情况乘上赔率比上失败的情况为：

由 (P(大)= (P(小)以及 (P(大)+ (P（小）= (P（围骰）=1，不难知道：

同样，计算“大”和“小”的胜利失败比乘上赔率：

下面考虑点数的投注方式的概率，首先考虑{4,5,6,7,8,}这五种情况的可能性，并且{17,16,15,14,13,}的可能性与之是对应相等的。利用挡板模型：用两个挡板将i个球分成三组，其中 84 ≤≤i ，每组的球的个数必然小于六个，对于每一种情况可能的构成方案总共有种。

当i=14或i=17，可能的概率为：

赔率乘上胜和负的比率为：

当i=5或i=16，可能的概率为：赔率乘上胜和负的比率为：

当i=6或i=15，可能的概率为：

赔率乘上胜和负的比率为：

当i=7或i=14，可能的概率为：

赔率乘上胜和负的比率为：

当i=8或i=13，可能的概率为：

赔率乘上胜和负的比率为：

对于点数为9与点数为12的情况，为了利用挡板模型，必须去除掉每组球多于六个的情况，当每一组的球的个数在少于六个时，每一种情况都与投掷骰子的情况一一对应。所有对于投掷三个骰子，点数之和为九的情况共有

则：

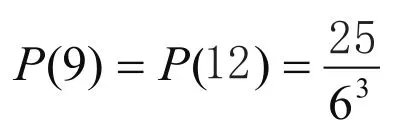
赔率乘上胜和负的比率为：

而点数之和是10和11的可能的组合是一一对应的，十个球分成三组，每组至少有一个球的挡板模型的可能的情况共有也就是36种情况，至少有一组有超过六个的球的情况共有9种，三个骰子总和为十的可能的情况总共有27种，则：

赔率乘上胜和负的比率为：

对于所有可能的情况，均有比率乘上赔率都是小于一这一结果，由于赌场是长时间存在的，可以假设赌场进行的赌局的次数足够的多。由大数定律，某一事件发生的次数变多时的时候，事件发生的频率会接近于事件发生的概率。考虑次数足够多的情况，可以用概率来代替频率。假设在所有的游戏中，赌徒获胜N次，失败M次，赔率是Q，游戏下注金额为A。在所有游戏中，赌徒所获得金钱是QNA，损失的金钱是MA，而获得的钱与损失的金钱的比例则是又由伯努力大数定律，进行的次数足够多时，可以用获胜的概率与失败的概率的比1P来代替有：

那么获得的金钱与损失的金钱的比例则近似于Q1P，其中的Q1P赔是赔率乘上胜和 负×的6:比21率6，-满25足=由大数定律来呈现，有：

也就是说当进行赌博的次数足够多的时候，获得的金钱都是少于失去的金钱的，在长期赌博骰宝的情况下，损失总是大于收益的，也就是总体呈现亏损的情况。

2 带灾难的投资策略

上一章我们分析了在长期的赌博行为中，最终的亏损以及破产的必然，其中一部分原因是由于赌场关于每种下注情况下的赔率的设置得比较低，另一部分原因是由于随机事件本身的特性，所以不确定性非常大。由此知道，人们不应该参与赌博，而应该考虑确定性更大的投资来降低风险。接下来我们将考虑一种确定性更大的情况的投资（其中确定性体现在对一些特定信息的掌握），以及讨论在控制风险的情况下，具体的最优策略。

假设在某个方面，需要进行总共z次的投资，而会有s次的灾难发生，并且只有z-s次的投资将是成功的，当灾难发生的时候，将失去所有投入的资金，当投资成功的时候，将获得等同于投入的资金的利益。为了控制风险，将使用投入的资金是本金的某个倍数的方式进行投资，当初始的本金为c时，为了最大化z次投资后的资金，投注的比率是多少，最后的资金是多少？

在这个问题中，和普通的赌博存在着以下几点的不同，如果一个赌博的胜率是那么在z局游戏中，获胜几次都是可能的，而在这一问题中，一定会并且只会投资成功z-s次，不同于赌博游戏的每次的独立性，这个问题中的投资成功或者遇到灾难，都是将会受到之前的投资的结果的影响，例如，当进行了z-1次投资后，最后一次的投资的结果是成功还是遇上灾难，是可以百分之百确定的，所以可以通过之前所发生过的情况来改变当前投资的策略。

同时，在整个过程中并不确定灾难会在那次投资中发生，也不知道每次投资时出现灾难的概率，所以为了控制风险，我们将需找出一种投资策略，使得每一种可能的灾难的情况所对应的最终资金的下界最大化。对于一个固定的投资策略，对于不同顺序的灾难情况，获得的最终资金是不同的，必定有一种灾难情况使得最终的资金最小，把这种灾难情况称为最坏情况，并把这种情况下的最终资金称为最坏情况资金，现在需要找出一种策略，使得它的最坏情况资金大于其他所有的策略。

首先考虑s=0的情况，也就是没有灾难发生的情况，首先考虑只进行一次投资的情况，显然，在这种条件下，这次投资应该投入所有的本金，所获得的资金是2c。更进一步的，对于 1≥z 的投资，在z次投资后，最终的资金为 2zc对于s=1的情况，在z次投资中的任何一次都可能出现，并且只有一次灾难，此时最佳的策略是在第一轮投入的资金，并且最终的资金为下面将给出证明。

首先考虑z=1的情况，对于只进行一次投资，并且灾难一定会发生的情况，最好的策略就是不投入任何的资金，这时最终的资金为z=1时结论成立。

假设z=k时都成立，当z=k+1时，假设第一次投资将投入本金的x倍，那么将会出现两种情况：1）灾难没发生在第一次投资，这时的资金变成c+x，并且在接下来k次投资中，将会有一次灾难发生，由假设，最终的资金将是灾难发生在第一次投资，这时的资金变成c-x，并且在接下来的投资中，将不会再有灾难发生，那么最终的资金为 )(2 xck- 。

为了找到使得最坏情况资金最大的策略，也就是使得最终资金的下界的最大，那么两种情况的最终资金应该相等，也就是：

解之得：

并且最终的资金：

结论得证。

接下来考虑s=2的情况，当进行 2≥z 次投资，并且将会出现s=2次灾难的时候，在首次投资时，应该投入最终的资金是下面将给出证明。

对于z=2，两次投资都将出现灾难，最好的方式就是不投入任何资金，最终资金结论成立。

假设当z=k时结论成立，当z=k+1时，假设第一次投资将投入本金的x倍，那么将会出现两种情况：1）灾难没发生在第一次投资，这时的资金变成c+x，并且在接下来k次投资中，将会有两次灾难发生，由假设，最终的资金将是灾难发生在第一次投资，这时的资金变成c-x，并且在接下来的投资中，将会再有一次灾难发生，那么最终的资金为

同理，为了找到使得最坏情况资金最大的策略，也就是使得最终资金的下界的最大，那么两种情况的最终资金应该相等，也就是：

解之得：

最终资金：

结论得证。

对于更加普遍的灾难次数s，可以通过已知的几种情况推导，为了更加直观地解决这个问题，首先定义TZS为在z此投资中，有s次灾难发生时，第一局投入的资金与本金最佳比例。EZS表示在这种投资策略下，最终的资金与初始资金的比例。

由前面所证明的，我们有：

对于任意的s，我们假设第一次投资将投入TZSc的资金，这时有两种可能的结果：1）第一次投资没有发生灾难，这时的资金为(1+TZS)c，而接下来的z-1次投资中，将会发生s次灾难，最终的资金为E(Z-1)s(1+TZS)c；2）灾难发生在第一次投资，这时的资金为(1-TZS)c，并且在接下来的z-1次投资中，将会发生s-1次灾难，最终的资金为E(Z-1)(S-1)(1-TS)c。

同理，为了找到使得最坏情况资金最大的策略，也就是使得最终资金的下界的最大，那么两种情况的最终资金应该相等，也就是：

也就是说：

化简并将TZS放在等式的一边，有：

带入上一个等式，可以得到：

至此，我们得出了EZS的递推表达式。

将递推式两边同时取倒：

两边同时乘上 2z-1次方：

下面通过数学归纳法证明：

由前面的证明，可得，当S-0,1,2时，对于所有的 sz≥ 均成立，我们不妨设s=j时，对所有的 sz≥ 成，则当s=j+1时，若z=j+1，意味着灾难发生在每一次投资，所以每一次都不应该投资，那么E(j+1)(j+1)=1，则B(j+1)(j+1)=2j+1，此时命题成立，再假设 lz=时成立，其中 1+＞jl ，由递推公式：

由此，当s=j+1时，对于所有 sz≥ ，命题都成立，所以对于任意的 0≥≥sz ，命题都成立。

因此可以得出：

同理还可以求得：

因此，在会有s次灾难的z次投资中，最优的最终资金是EZSc，并且最优的投策是，每一次投资的金额Tnmg，其中n表示的是还剩下投资次数，m表示还发生的灾难的次数，g表示这次投资开始之前所拥有的资金数。

如果不按照这个策略进行投资，当投资的金额多于Tnmg时发生灾难，或者投资的金额少于Tnmg没发生灾难，都将导致最终的资金少于EZSc。

例如，在十二个月中，政府需要对房子建设进行十二次投资，通过预测发现将会有三个月有暴雨，在有暴雨的月份，进行的投资都会亏损，那么这种情况下，为了控制风险，就可以应用我们的模型来解决每个月投入都少资金的问题。

3 结论

通过概率的分析，了解到普遍存在的直觉的错误，人们对某些随机事件的结果有一些错误的估计，原因是由于对样本空间的选择错误造成的。直觉与实际情况不符合是大部分人参与赌博的原因，同时计算了在获胜概率不等时，并且以在赌场比较流行的骰宝为例，得出了胜负比率乘上赔率小于1这一结论。进行足够多次的赌博，最终的结果必然是破产的。由此看出，赌局的设置导致了长期赌博亏损的必然。进一步，提出了在多次投资中，将会遇到固定次数的灾难的情况中，如何进行每一轮的投资，才能在控制风险的情况下，使得最终的资金最大的投资策略。

[1] 林志兴. 概率与直觉[J]. 数理统计与管理, 2006, 25(2):240-243.

[2] 王俊红. “免费抽奖”真的免费吗?——某个抽奖活动中的概率统计问题[J]. 数学的实践与认识, 2009, 39(2):199-201.

[3] 彩票与概率分析[J]. 统计与咨询, 2006(2).

[4] 张国辉. 从赌博和概率到抽奖陷阱中的数学[J]. 科技信息, 2009(1):162-163.

[5] 冯金顺. 用数学知识解析赌博的实质[J]. 商丘职业技术学院学报, 2014(5):1-3.

[6] 夏恒. 赌博·游戏·战争与数学[J].青海民族大学学报:社会科学版, 1993(4):102-105.

[7] 胡晓飞. 赌博产生的数学——概率论的起源和发展[J]. 科技风, 2013(18):189-189.

[8] 张少华. 赌博中的数学[J]. 百科知识, 2010(9):17-18.

[9] 隋圆圆. 赌博策略及其在资金管理中的应用[J]. 山东大学学报:理学版, 2013, 48(5):97-104.

An Analysis of Investment Strategy: from Random Events to Disaster

Nong Yu-xuan
(School of mathematics and statistics, Central South University, ChangSha China, 410075)

This paper is exemplified by a popular dice game in casinos. Supposing the conditions are met with the ratio of winning and losing being multiplied by odds, the study investigates the conditions of profits and loss given by two different betting strategies, the results show that the gamblers will eventually lose. And the author proposes a further investment question which is more certain than the gambling results. That is , during the fixed and multi-turned investments, how the profits can be gained to the largest extent when the risks are under control and the numbers of disaster to take place are already known. This paper also analyzes the specific strategies during every turn of investment and the final situation of profit obtaining when investment equals the profits in return.

intuitive error; probability theory; investment with disaster

O1-647

A

1674-3083（2016）06-0069-07

2016-11-24

农宇轩（1994—），男，广西平南人，本科，研究方向：数学与应用数学。