具有连续时滞和功能性反应的微分方程的概周期解
严建明
(湖南财政经济学院数学与统计学院 湖南 长沙 410205)
众所周知,在种群动力学的研究中,种群的持续生存和灭绝是人们非常关注的课题. 近年来,对于扩散对种群的持续生存的影响已有不少的结果,人们通过扩散可以挽救绝灭的种群,从而使其保持持续生存.1965年,Holling在实验的基础上,对不同的物种,提出了三种不同的功能性反应函数.对具有Holling I、II、III类功能性反应的系统,许多学者进行了深入研究[1,2].由于概周期现象在实际问题中经常可见,以周期现象作为特例,它是比周期现象更广泛的现象。对于 Lotka-Volterra系统的概周期解的定性性质(概周期解的存在唯一性和一致渐近稳定性)的研究工作目前相对还较少[3,4,5,6].而对于同时具有连续时滞、扩散、HollingⅡ类功能性反应的Lotka-Volterra型竞争系统的研究就更少,本文就研究这种具有连续时滞、扩散、HollingⅡ类功能性反应的非自治竞争模型:
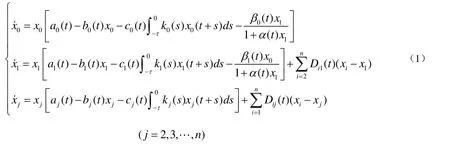
其中 ai( t), bi( t), ci( t), Dij( t)( i = 0,1,… ,n, j = 1,2,… n ) ,α(t )是连续的严格正的函数.x0和 x1分别表示两个竞争种群 X0和 X在斑块 1中的密度, xj( j = 2 ,3,… ,n )是种群 X在斑块j中的密度. Dij( t)( i, j = 1 ,2,… ,n )表示种群 X在斑块之间的扩散系数. ki( s)是分段连续函数,并且

记fL=inf f( t), fM= s up f( t ).本文我们假定方程(1)的系数满足下列条件:
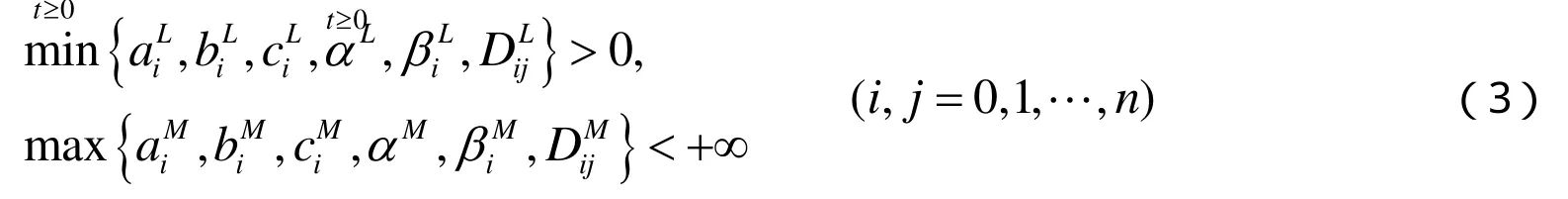
为了叙述的方便,我们作如下记号: 记
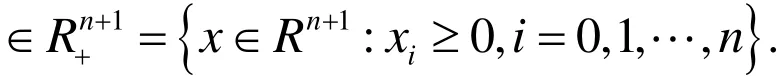
C+表示定义在[- τ ,0]上具有范数(其中代表欧几里德范数)的非负连续函数构成的Banach空间.因此,如果我们选C+为系统(1)的初始函数空间,易知对且则系统(1)在上存在唯一解 x ( t,φ),且对于有我们称此解为系统(1)的正解.因此,在本文下面的研究中,我们总假定

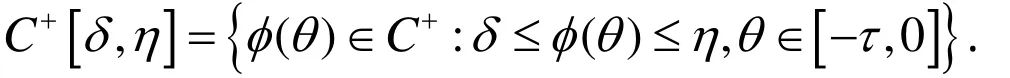
对于系统 (1),记 x( t)= x(0,φ )(t)是过(0,φ)的解,其中初值函数则 x ( t) 是唯一的,且 x ( t) > 0 ,t ∈ [ 0 ,T ),这里[0 ,T ) 是系统(1)的解的最大存在区间,这样的解叫做系统(1)的正解.系统(1)的系数是连续的严格正的概周期函数.
引理1[7]考虑泛函微分方程

及乘积系统
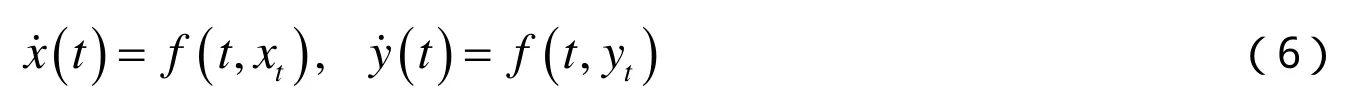
这里 f :R× C→R3连续,对于φ∈C,定义范数为这里为 R3中的范数.令
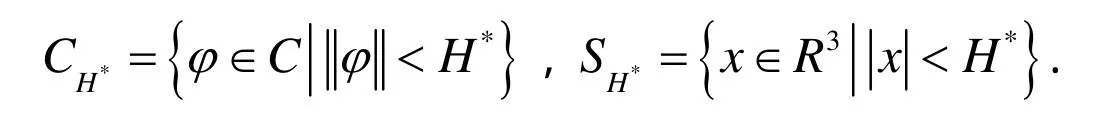
这里总是假设对φ关于t是一致概周期的,若存在连续函数
V:满足如下条件:
(Ⅰ)其 中 a( s),b ( s) ∈ C IP, b (0 ) =0;
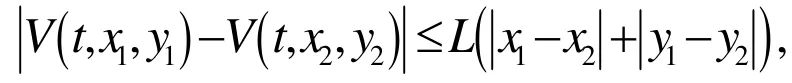
(Ⅲ) 存在连续非减函数 p ( s) ,当 s > 0 时,有 p ( s)> s,使得当
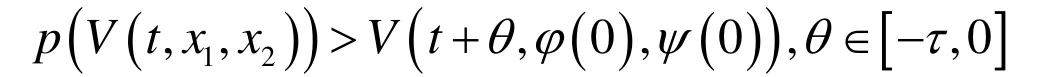

对系统(1)作如下变换则系统(1)可化为如下等价系统:
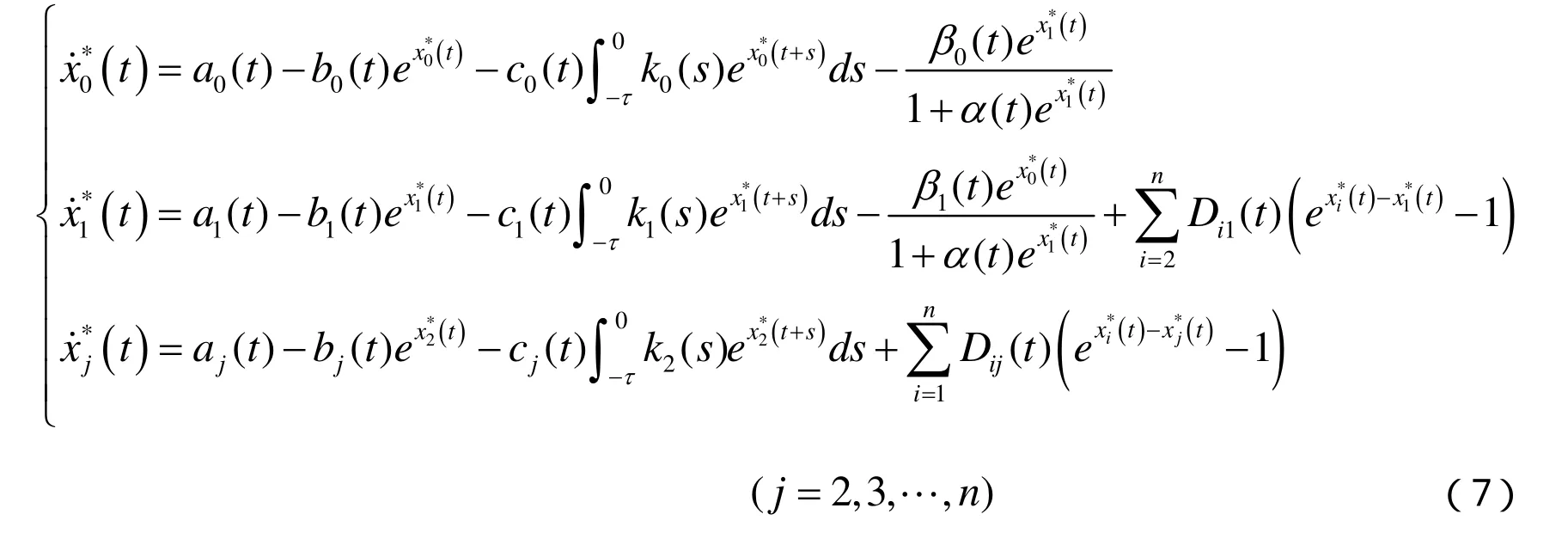
定理 设系统(1)满足以上给定的条件(2)(3),且还满足
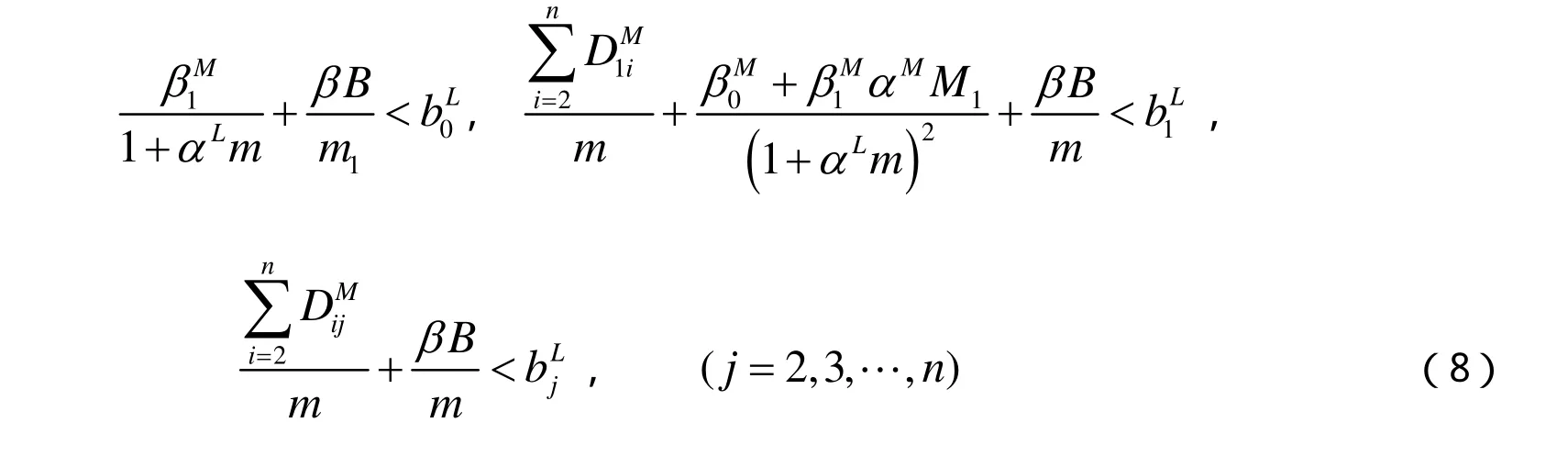
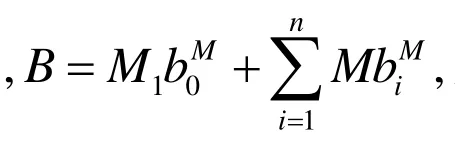
证明 考虑系统(1)的乘积系统
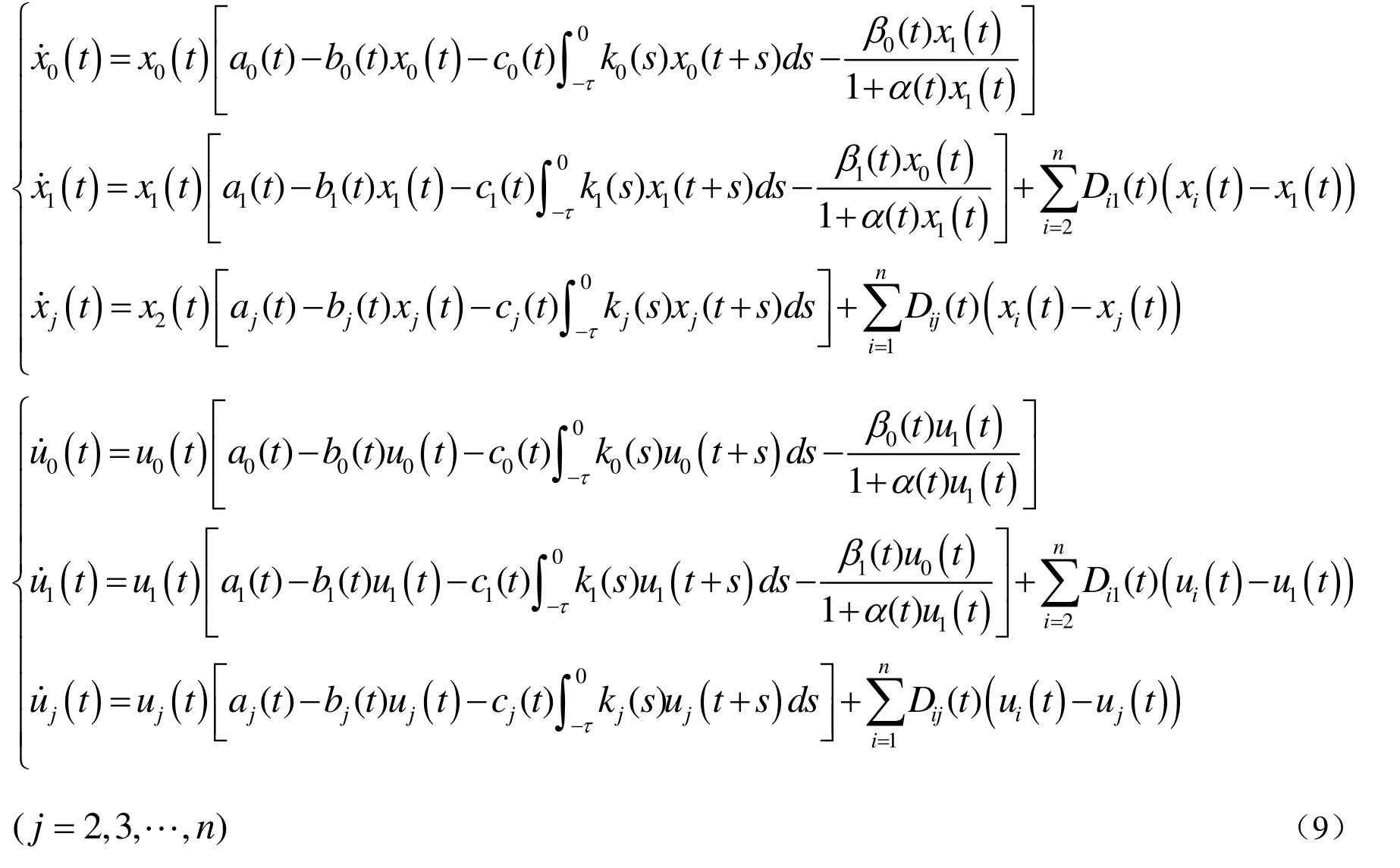
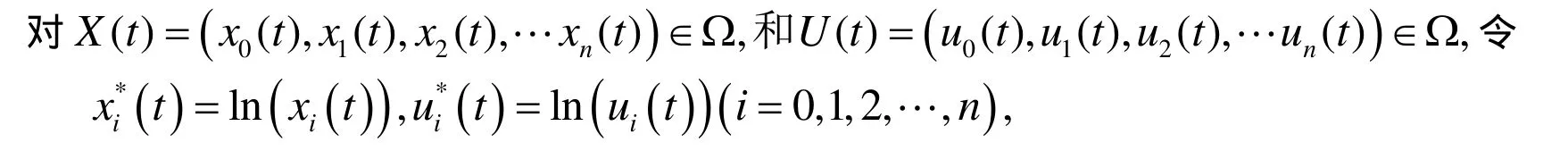
定义集合
Ω*可知Ω*是系统(7)的最终正向不变集.则这里的Ω, Ω*如前面所定义.
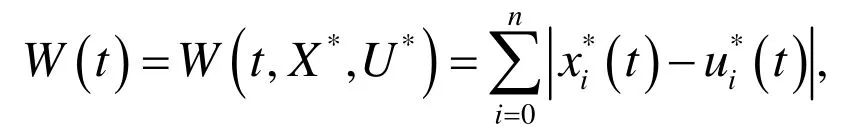
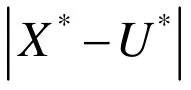
对于乘积系统(9)在Ω×Ω上的任一解

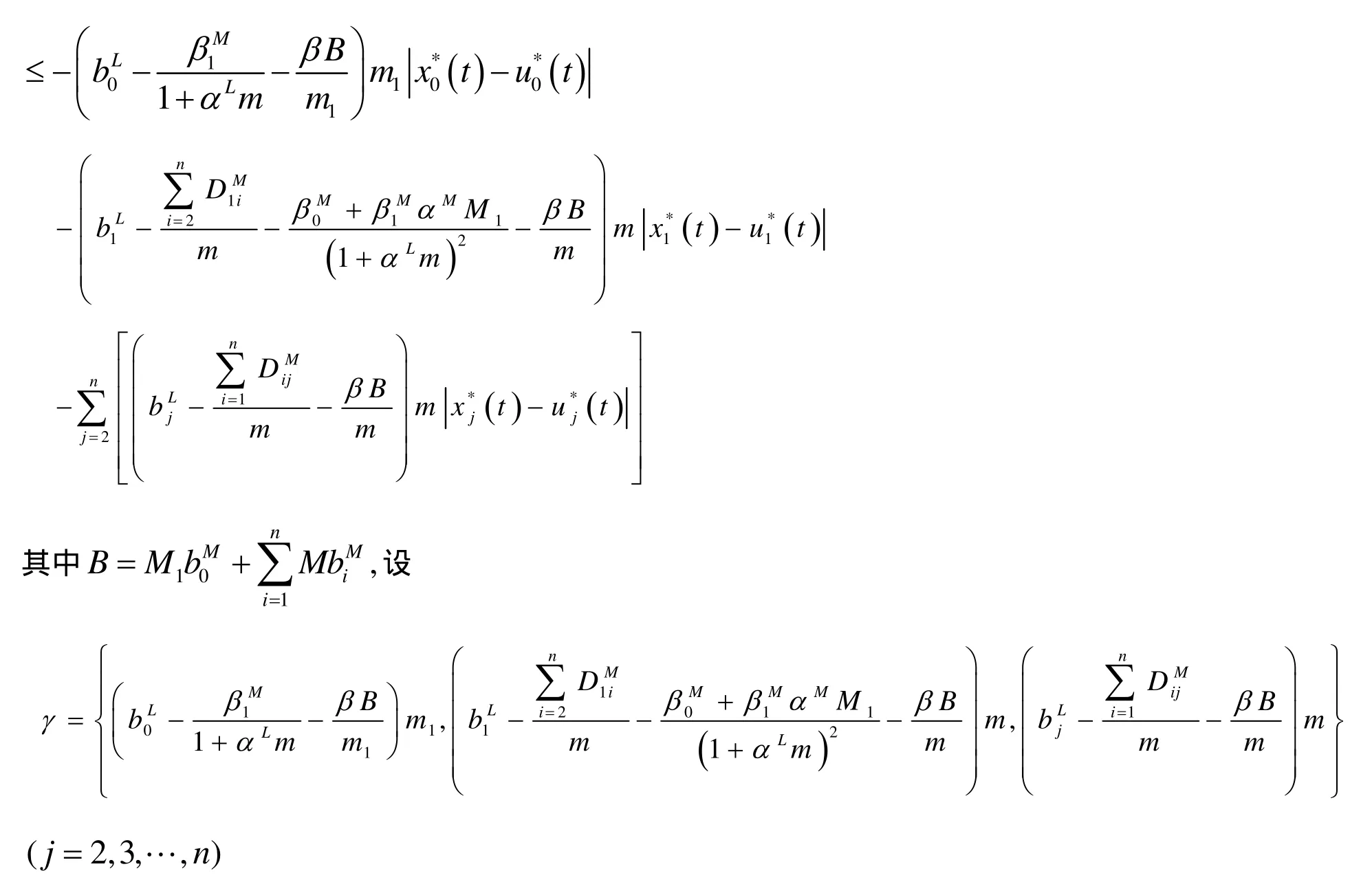
从而由条件(8)可知存在常数γ>0,使得有
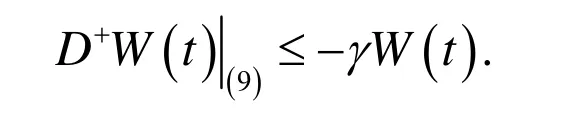
由引理 1知,系统(1) 在区域Ω中存在一致渐近稳定的概周期解,进而如果系统(1)的右端关于t是ω-周期的,则系统(1)存在一个ω-周期解.
[1]靳祯,原三领,马知恩.具有功能性反应的三种群食物链系统全局周期解的存在性[J].工程数学学报,2001,18(04):69-75.
[2]桂占吉,陈兰荪.具有功能性反应的非自治竞争系统持续性[J].工程数学,2001,17(02):07-10.
[3]罗桂烈.具时滞的非自治扩散捕食系统的概周期解[J].生物数学学报,1998,13(01):32-38.
[4]罗桂烈,廖民锂,江佑霖.两种群非自治 Lotka-Volterra竞争扩散系统的概周期解[J].系统科学与数学,1998,18(02):204-210.
[5]Zhang Jingru,Chen Lansun.Periodic solutions of single-species nonautonomous diffusion models with continuouse time delays[J].Math.comput.modelling,1996,23(07):17-27.
[6] 杨启贵,江右霖.Willis环状脑动脉瘤模型的概周期解[J].生物数学学报,2000,15(03):313--318.
[7]Yuan Rong.Existence of almost periodic solution of functional differential equations[J].Ann.of Diff.Eqs.1991,07(02):234-342.

