基于主成分分析的神经网络算法对期权价格预测研究

骆 桦，刘 兴

(浙江理工大学理学院，杭州 310018)

基于主成分分析的神经网络算法对期权价格预测研究

骆 桦，刘 兴

(浙江理工大学理学院，杭州 310018)

采用基于主成分分析的神经网络算法对华夏上证50ETF期权价格进行预测，并使用期权数据验证该方法的有效性。比较传统Black-Scholes期权定价、单个BP神经网络算法和基于主成分分析的BP神经网络算法对期权价格的预测精度，结果表明：基于主成分分析的BP神经网络算法预测精度最高，传统的Black-Scholes期权定价方法其预测精度最低。

期权价格；Black-Scholes期权定价；主成分分析；BP神经网络

0 引 言

金融市场中的期权是重要的金融衍生品，期权交易始于18世纪后期的美国和欧洲市场，1973年芝加哥期权交易所进行标准化合约的买卖后，期权得到迅猛发展。期权又被称作选择权，是指在未来一定期限内可以买卖某种资产的权利，期权的买方向卖方支付一定的期权费，拥有在未来一段时间或者特定时期以事先约定好的价格向卖方买入或者卖出一定数量的标的资产的权利。期权价格变动影响着市场中投资者的利益，因此预测期权价格非常重要。2015年2月9日，中国大陆市场诞生了唯一一只可交易期权——华夏上证50ETF期权，研究该期权的价格变动对中国市场的投资者来说具有重要意义。

常用的期权价格预测方法有时间序列、BP神经网络等。时间序列方法中典型模型是ARMA模型[1]。李干琼等[2]利用时间序列模型对农产品市场价格进行短期预测，模型预测误差为10%；马保忠等[3]利用时间序列分析对黄金期货价格进行拟合；尹玥[4]利用ARIMA模型对股票市盈率分析并预测。由于时间序列模型是一种线性模型，而期权价格呈现非线性，因此利用时间序列分析来研究期权价格有一定的缺陷。BP(back propagation)神经网络是一种按照误差逆传播算法训练的多层前馈网络，能够学习和储存大量的输入-输出模式映射关系，在对各种随机数据的拟合和预测上有着广泛的应用。董莹等[5]利用BP神经网络来预测标准普尔500指数期权；韦德民等[6]在Black-Scholes期权定价公式基础上构建神经网络，对中国市场上的权证价格进行研究；王启敢等[7]通过实证表明，人工神经网络在我国权证市场上的定价效果优于Black-Scholes期权定价方法；Laboissiere等[8]利用人工神经网络以及相关性分析来预测公司的股票价格。尽管很多研究表明利用BP神经网络算法能提高精度，但是大多没有考虑输入输出变量的设计。

本文提出了一种基于主成分分析的BP神经网络算法来研究期权价格变动。构建BP神经网络的重点在于输入输出变量的设计，本文对期权价格预测研究时，先对输入变量进行主成分分析，得到贡献率较大的变量作为BP神经网络的输入变量，这样可减少输入变量的维数，优化神经网络结构，进而提高预测精度。本文以50ETF期权价格为实证分析验证该方法的可行性，同时比较传统Black-Scholes期权定价方法、单个BP神经网络算法和基于主成分分析的BP神经网络算法3种方法的期权价格预测精度，以验证本文所提出算法的有效性。

1 实验数据来源及输入输出变量设计

本文选择中国大陆市场唯一上市可交易的期权——上证50ETF期权作为研究对象。该期权合约标的是华夏上证50ETF(代码为510050)，合约的履约方式为欧式，合约的到期月份为当月、下月及最近的两个季月，合约的最后交易日和行权日为合约到期月份的第4个星期三。本文以看涨期权为例，选择50ETF购6月2.50(代码为10000464)及其标的资产自2015年11月5日到2016年3月17日的每日收盘价为样本数据(数据来源于WIND资讯)，该数据分别包含90个交易日数据，其中前80个交易日的数据记为样本内数据，后10个记为样本外数据。50ETF购6月2.50指的是2016年6月22日交割，执行价为2.50的看涨期权。50ETF购6月2.50每日收盘价格序列如图1所示。

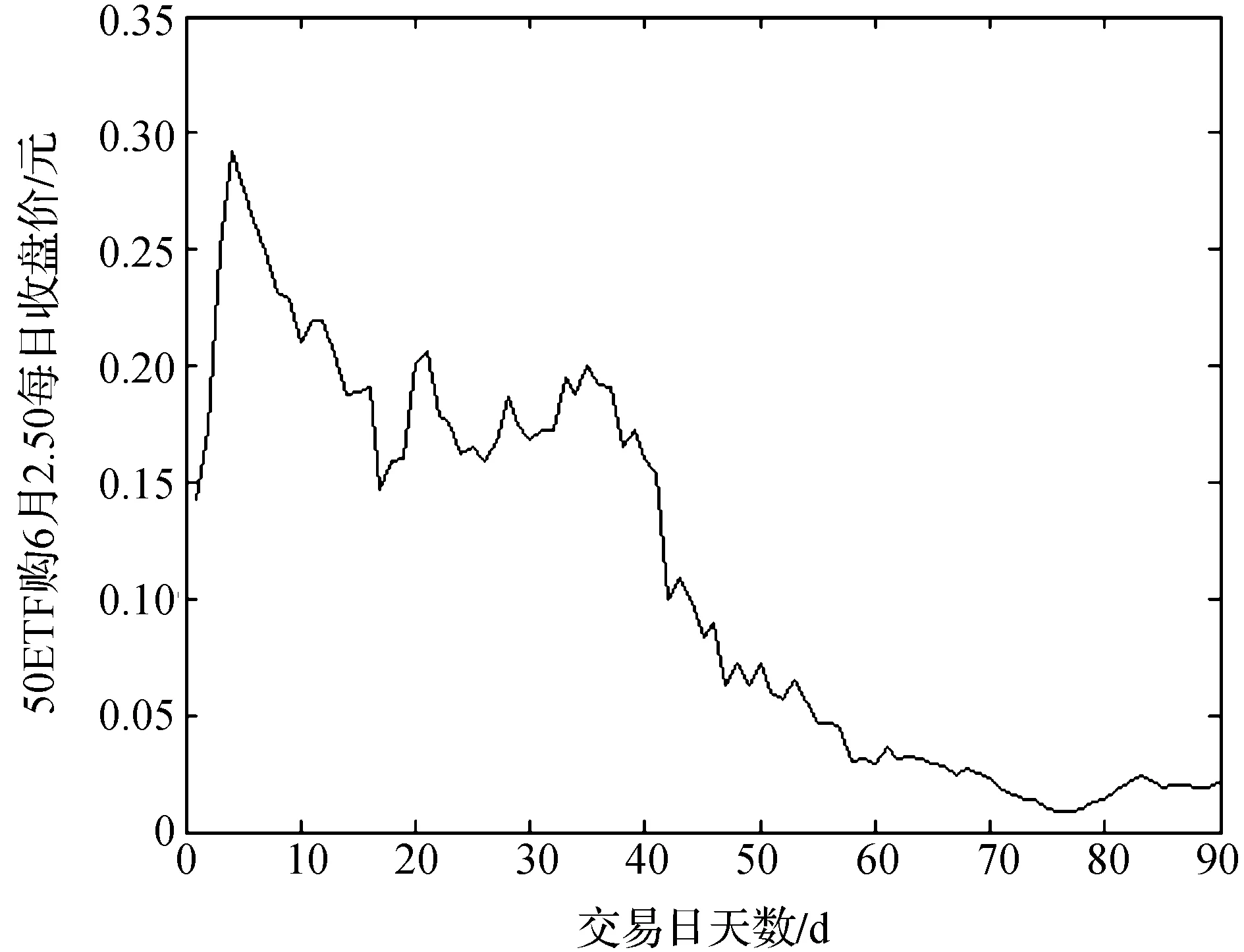
图1 50ETF购6月2.50每日收盘价格

50ETF购6月2.50的每日收盘价作为神经网络的输出变量。考虑各影响因素以及滞后效应，本文选择以下变量作为神经网络输入变量：期权标的资产分别滞后1、2、3、4、5d的价格、执行价格、资产价格5d波动率和上海银行间同业拆放利率Shibor 1年，共8个变量。这8个变量自2015年11月5日到2016年3月17日的数据来源于WIND资讯。

2 建立基于主成分分析的BP神经网络算法的期权价格模型

2.1 基于主成分分析的BP神经网络算法

主成分分析[9]是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量称为主成分。在实际问题中，总体X的协方差矩阵Σ通常未知，需要由样本进行估计。设x1,x2,…,xn为取自总体X的样本，每个样本有p个指标，则样本xi可以表示为p维向量，即：

xi=(xi1,xi2,…,xip)T(i=1,2,…,n).

其中元素xij(j=1,2,…,p)表示描述该样本的一个指标。样本表示为X=(x1,x2,…,xn)T。记样本协方差矩阵S为：

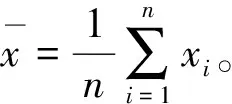
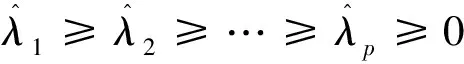
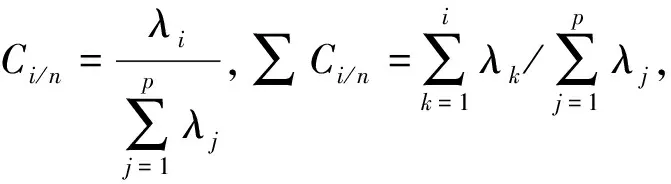
BP神经网络算法[10]由信号的正向传播和误差的反向传播两个阶段组成。在正向传播过程中，信号从输入层输入，经过隐含层处理之后从输出层输出。如果从输出层输出的结果跟预期结果误差大，则转入反向传播过程，将输出结果误差按照一定形式沿着网络反向传播，并且按照误差函数的负梯度方向不断修正各层的连接权值以及阈值，直至输出误差达到精度要求，从而实现神经网络中的大量的输入输出的非线性映射。

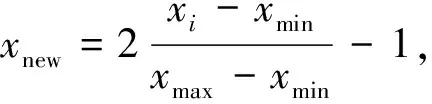
2.2 基于主成分分析的BP神经网络算法的期权价格模型的建立与结果

模型变量包括期权标的资产价格分别滞后1、

2、3、4、5 d值，执行价格、资产价格5日波动率以及上海银行间同业拆放利率Shibor 1年，共8个变量。首先对这8个变量做主成分分析，将8个变量所包含的样本数据进行归一化处理后，得到它们对应的特征值为：0.0061、1.9000、0.6391、0.6288、1.0062、1.3185、1.2965、1.2048。将这些特征值排序并计算贡献率，结果见表1。

表1 输入变量贡献率结果表

计算得前6个特征值对应的贡献率累计达到92.07%，因此主成分有6个。对应于BP神经网络的输入变量设计上，本文选择表1中前6个特征值对应的变量为输入变量，即期权标的资产价格分别滞后2、3、5d值，执行价格、资产价格5日波动率以及上海银行间同业拆放利率Shibor1年，共6个输入变量。

利用这6个输入变量数据构造BP神经网络，训练参数如下：输入层到隐含层的传递函数为tansig，隐含层到输出层的传递函数为purelin；动量项系数为0.3，最大学习次数为5000，学习速率为0.25；网络输出与真实值之间的误差采用均方误差。初始权值和阈值为(-1,1)之间服从均匀分布的随机数，通过多次试验确定隐含层的神经元个数为5个。基于主成分分析所构建的BP神经网络结构为6-5-1。

图2是基于主成分分析的BP神经网络输出值与实际值的比较结果，从图中可以看出输出值与实际值的误差较小，这说明所构建的BP神经网络效果良好。利用构建好的BP神经网络结构可预测出后10个交易日的期权价格，结果见表3。

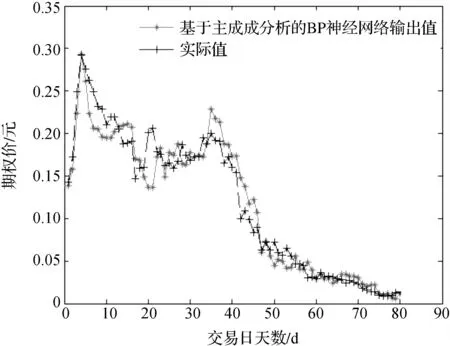
图2 基于主成分分析的BP神经网络输出值与实际值比较

3 与两种传统期权价格预测模型比较

3.1 Black-Scholes期权定价

利用Black-Scholes随机微分方程[11]得到的期权定价公式是一个连续时间的金融衍生品的定价模型。由于金融衍生品价格满足Black-Scholes微分方程：

(1)

再结合边界条件，可以求出金融衍生品的价格。以欧式看涨期权为例，其价格为：

f(t,St)=StΦ(d1)-Ke-r(T-t)Φ(d2)

(2)

其中：

在应用Black-Scholes微分方程计算金融衍生品的理论价格时，本文作了如下假设：a)金融衍生品的剩余期限T-t的单位为年份；b)所采用的无风险利率r为年利率；c)基础资产收益率的标准差σ亦为年标准差，σ的计算方法如下：

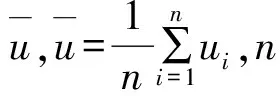
这里采用上海银行间同业拆放利率Shibor1年的60日均值3.2471%作为无风险利率值，由期权合约标的资产的样本内数据计算得到收益率的年标准差σ为0.3307。以2016年3月3日到2016年3月10日的合约标的资产价格，由式(2)通过计算可得后10个交易日的期权计算价格，结果见表2。

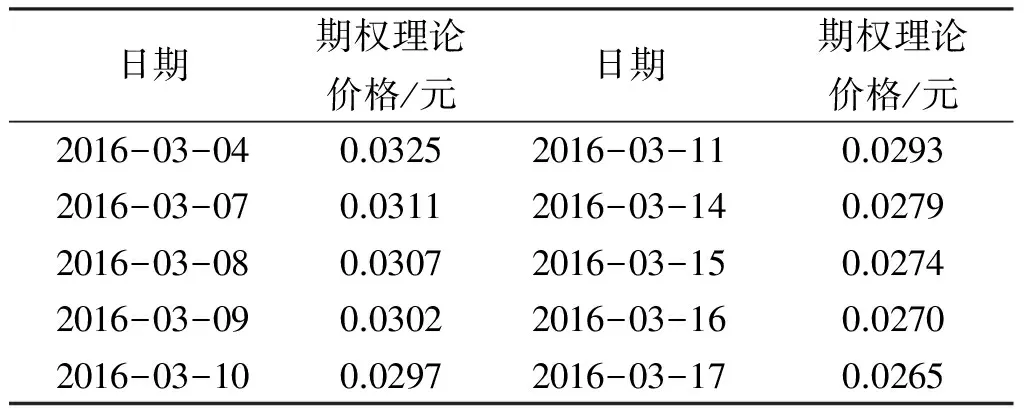
表2 基于Black-Scholes期权定价模型的50EFT购6月2.50的理论价格

3.2 单个BP神经网络期权价格预测

BP神经网络的输入变量个数为8个，网络训练参数设置如下：输入层到隐含层的传递函数为tansig，隐含层到输出层的传递函数为purelin；动量项系数为0.3，最大学习次数为5000，学习速率为0.25；网络输出与真实值之间的误差采用均方误差。初始权值和阈值为(-1,1)之间的服从均匀分布的随机数，通过多次试验最终确定隐含层的神经元个数为6个。因此构建的BP神经网络结构为8-6-1，由构建好的BP神经网络结构可预测出后10个交易日的期权价格，结果见表3。

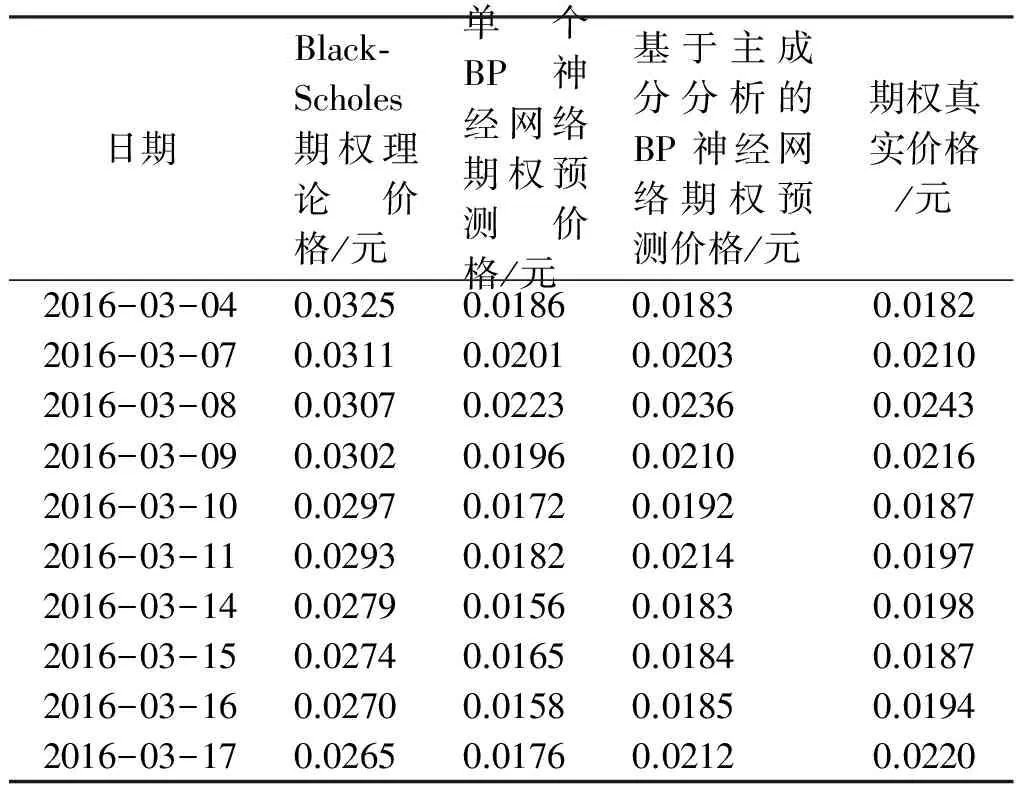
表3 传统期权价格预测模型与基于主成分分析的BP神经网络预测模型结果比较

3.3 结果比较

表3是传统期权价格预测模型与基于主成分分析的BP神经网络期权价格预测模型结果比较，比较这3种方法的优劣性，优劣性由误差大小来判定，误差较小的方法较优。本文选取两种误差，一是均方误差MSD，二是平均绝对误差MAD，它们的计算公式如下：

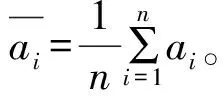
通过计算，得到3种方法的误差见表4。

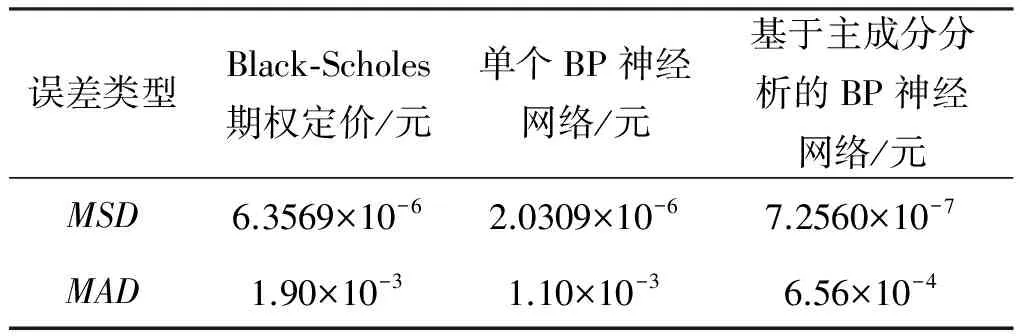
表4 3种方法预测期权价格误差比较

从表4中可以看到：应用Black-Scholes期权定价模型得到的期权计算价格与实际值之间的误差较大，其均方误差MSD为6.3569×10-6，平均绝对误差MAD为1.90×10-3；通过构建单个BP神经网络算法以及基于主成分分析的BP神经网络算法来预测期权价格得到的预测值与实际值间的误差均较小；这三种方法中均方误差和平均绝对误差最小的是基于主成分分析的BP神经网络算法。可见基于主成分分析的BP神经网络算法对期权价格预测可行，且其预测精度最高。

4 结 语

本文提出基于主成分分析的BP神经网络算法对期权价格预测研究，利用主成分分析对BP神经网络中的输入变量进行优化，减少输入变量维数，降低神经网络结构复杂度，提高神经网络的预测精度。实验结果表明，利用单个BP神经网络算法对期权价格预测研究，其预测精度比传统的Black-Scholes期权定价方法高，而基于主成分分析的BP神经网络算法其预测精度比单个BP神经网络算法高。因此本文采用的基于主成分分析的BP神经网络算法对期权价格预测研究可行，且该方法的预测效果好。

[1] Fuchs J J. On estimating the order of an ARMA process [J]. Automatica,1987,23(6):779-782.

[2] 李干琼,许世卫,李哲敏,等.农产品市场价格短期预测方法与模型研究：基于时间序列模型的预测[J].中国农业大学学报,2011,16(2):172-178.

[3] 马保忠,甄博倩.基于时间序列分析的黄金期货价格预测模型的实证分析[J].商,2015(7):152.

[4] 尹玥.基于ARIMA模型的股票市盈率分析及预测[J].合作经济与科技,2015(2):36-37.

[5] 董莹,乌日噶,齐淑华.基于BP神经网络的期权定价模型[J].鲁东大学学报,2013,29(3):196-199.

[6] 韦德民,薄晓旭.基于人工神经网络的权证定价模型研究[J].市场经济与价格,2015(5):40-44.

[7] 王启敢,张艳峰.基于神经网络方法的期权定价研究[J].中南财经政法大学研究生学报,2009(5):49-53.

[8] LABOISSIERE L A, FERNANDES R A S, LAGE G G. Maximum and minimum stock price forecasting of Brazilian power distribution companies based on artificial neural networks[J]. Applied Soft Computing,2015,35:66-74.

[9] 何东,刘瑞叶.基于主成分分析的神经网络动态集成风功率超短期预测[J].电力系统保护与控制,2013,41(4):50-54.

[10] 王小川.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:1-19.

[11] BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. Journal of Political Economy,1973,81(3):637-659.

(责任编辑： 康 锋)

Study on Option Price Forecasting with Neural Network Algorithm Based on Principal Component Analysis

LUOHua,LIUXing

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Neural network algorithm based on principal component analysis was applied to forecast the option price of Chinese Shanghai 50 ETF, and the option data were used to verify the effectiveness of the proposed method. Besides, we compared prediction accuracy among traditional Black-Scholes option pricing, single BP neural network algorithm and the BP neural network algorithm based on principal component analysis. The results show that the BP neural network algorithm based on principal component analysis has the highest prediction accuracy, and traditional Black-Scholes option pricing method has the lowest prediction accuracy.

option price; Black-Scholes option pricing; principal component analysis; BP neural network

10.3969/j.issn.1673-3851.2017.01.020

2016-05-10

日期： 2017-01-03

国家自然科学基金项目(11401532)

骆 桦(1962-)，男，浙江诸暨人，副教授，硕士，主要从事金融数学和数理统计方面的研究。

F830.91

A

1673- 3851 (2017) 01- 0122- 05