凸轮滑块式夹紧机构设计及其热-结构耦合分析
竺 熔,俞亚新,周志栋,刘 磊
(浙江理工大学机械与自动控制学院,杭州 310018)
凸轮滑块式夹紧机构设计及其热-结构耦合分析
竺 熔,俞亚新,周志栋,刘 磊
(浙江理工大学机械与自动控制学院,杭州 310018)
为了满足摩托车制动蹄自动化生产要求,实现摩擦片与蹄形铝块之间夹紧并在高温下保压,设计了一种凸轮滑块式夹紧机构。通过对夹紧机构运动学和动力学仿真分析,获得了凸轮转速和输送速度对夹紧力的影响。对夹紧状态下的制动蹄在保温箱内进行温度场和应力场耦合分析,得到夹紧机构和工件的位移变化情况。结果表明:在热-结构耦合状态下夹紧滑块位移较常温下增加了0.7 mm,夹紧力增大了11.6 N。由于夹紧机构的结构特点,夹紧力的变化不会影响夹紧机构的正常松开,故该夹紧机构能满足高温环境下的工作要求。
夹紧机构;制动蹄;运动仿真;热-结构耦合
0 引 言
摩托车制动蹄生产中摩擦片和蹄形铝块通过胶粘剂粘合,胶粘剂固化需要放入200 ℃的恒温箱中,施加一定压力并持续45 min,才能在整个粘接面上得到一层厚度均匀的致密胶层[1]。目前摩托车制动蹄生产过程中涂胶、加压、松开等工作均由人工完成,这些工作属于劳动密集型的工作,劳动强度大,迫切需要采用机械化生产方式。根据制动蹄生产特点及自动化生产要求,可以采用夹具完成对制动蹄自动加压并松开的操作。
目前运用于实际生产的夹具机构主要有斜楔夹紧机构、螺旋夹紧机构、偏心夹紧结构、铰链夹紧机构等[2]。许多研究者对夹紧力优化进行了研究:刘少岗等[3]利用构造的摩擦力和摩擦力矩的圆锥,分析工件滑动情况,计算滑动过程中工件所受到的最小夹紧力;秦国华等[4]通过对夹紧状态下工件变形的研究,提出了一种工件位置误差与运动副变形之间的关系模型,为实现夹紧力的优化设计提供了理论依据。但是,对于夹具机构经历温度变化所引起的夹紧力变化的研究未见报道。
针对机构在经历温度变化时的应力场、温度场分析常采用热-结构耦合分析技术。李涵武等[5]、包圳等[6]借助ANSYS仿真软件,对处于单独机械载荷作用以及机械载荷和热载荷共同作用两种工作状态下的汽车制动器,分别进行结构和热-结构耦合分析,发现温度对制动器的强度与刚度均有较显著的影响,这为处于热环境下机构的结构设计提出了新的分析方法。齐先坤等[7]、杨淑贞等[8]、梅益等[9]将热-结构耦合分析应用于温度场、应力场共同作用下,行星齿轮组、减速箱等结构应力分布计算的场合。李昱霖等[10]通过瞬态热传导、热结构、热模态和热颤振之间的单向耦合关系,对飞行器热弹性问题进行分析,对处于气动热结构耦合状态下机构的分析,提出了一种新的思路。
本文根据某摩托车制动蹄自动化生产要求,设计了一种凸轮滑块式夹紧机构,阐述了实现自动夹紧的原理,分析了工件在受热后所受夹紧力的变化情况。
1 夹紧机构设计
1.1 夹具设计要求
结合制动蹄胶粘剂的胶合特性以及制动蹄生产效率方面的要求,制动蹄夹具的结构设计需满足如下2个条件:
a)所设计的夹具需提供80 N的夹紧力,并且随制动蹄一起进入200 ℃恒温箱中保温45 min;
b)传输带上每行设计6套制动蹄同时夹紧,行间距为200 mm。
1.2 机构原理分析
本文所设计的制动蹄夹具夹紧原理如图1所示,制动蹄由蹄形铝块5和摩擦片7组成,置于加压滑块1和限位圈6中间,弹簧受力后通过加压滑块1对制动蹄施加压力,制动蹄受到限位圈6的约束,因限位圈6与制动蹄外圈贴合,施加压力均匀地分布在制动蹄的胶合面4(蹄形铝块与摩擦片的胶粘面)上。
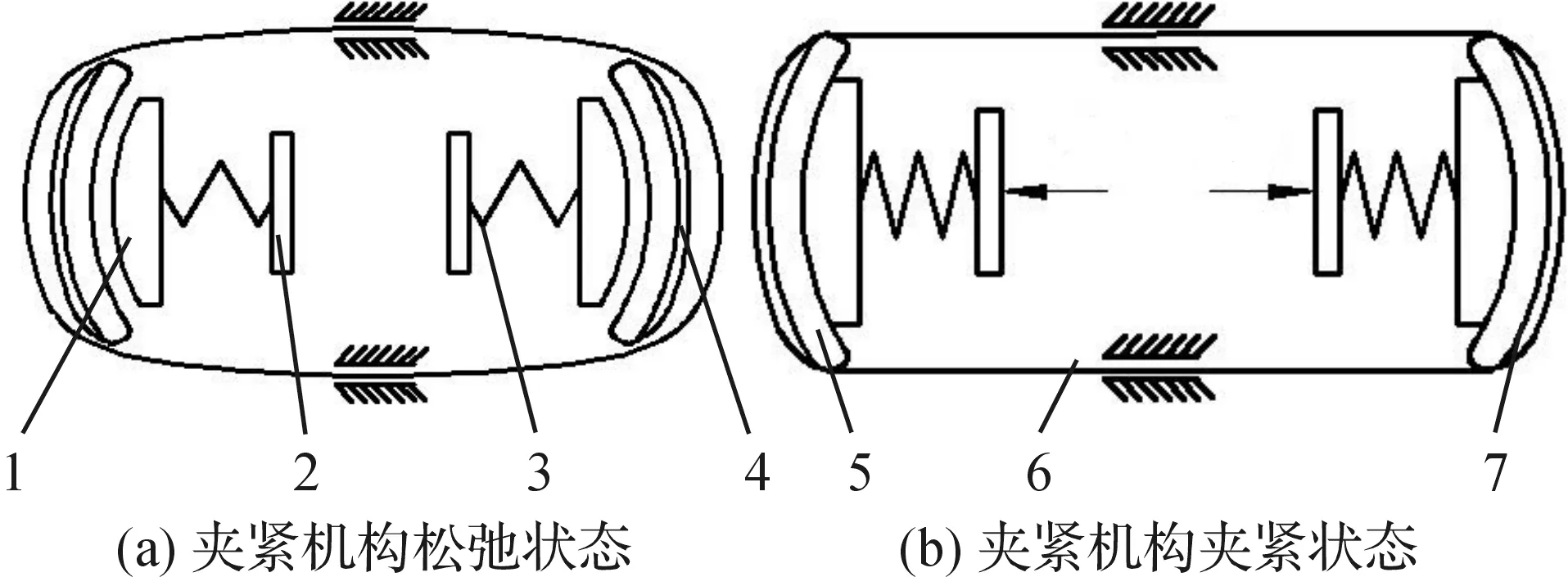
1.加压滑块;2.滑块;3.弹簧;4.胶合面;5.蹄形铝块;6.限位圈;7.摩擦片图1 夹紧机构原理
凸轮滑块夹紧机构如图2所示。已涂胶的摩擦片和蹄形铝块放入限位圈10与弹簧底座8中间,随着传输带11运动到夹紧凸轮1处时,夹紧凸轮顶杆下压,楔块3撑开夹紧滑块9,同时,保压滑块6在保压弹簧5作用下上升,限制夹紧滑块9的回复,摩擦片和蹄形铝块在限位圈10、弹簧底座8、夹紧弹簧4等一系列构件的作用下被压紧,随后进入保温箱并保压保温一定时间。制动蹄随传输带离开保温箱后运动到松开凸轮12下方时,松开凸轮顶杆13下压,顶下保压滑块6,夹紧滑块9在夹紧弹簧4的作用下回复原位,制动蹄与限位圈松开。
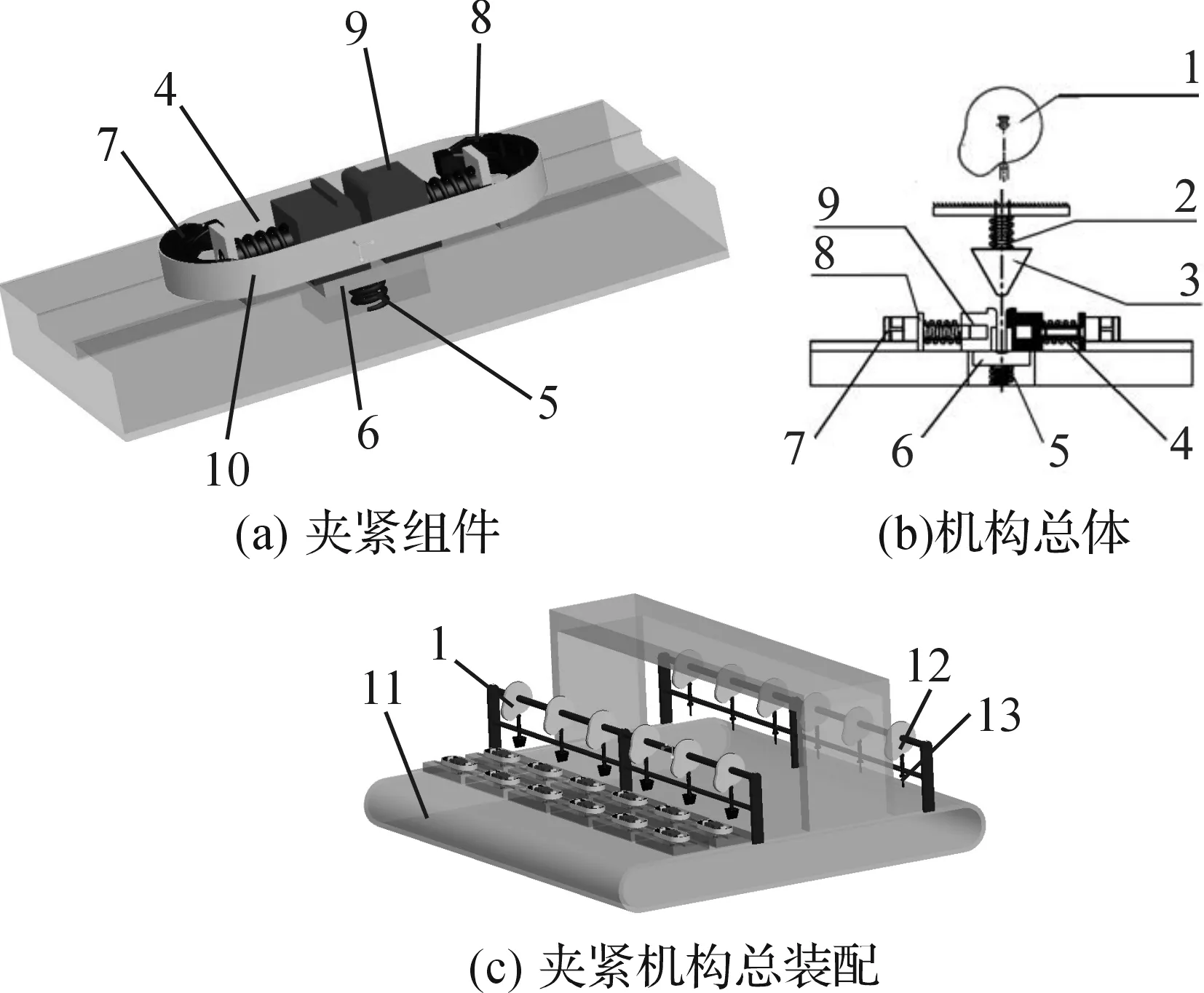
1.夹紧凸轮;2.回复弹簧;3.楔块;4.夹紧弹簧;5.保压弹簧;6.保压滑块;7.制动蹄片;8.弹簧底座 9.夹紧滑块;10.限位圈;11.输送带;12.松开凸轮;13.松开凸轮顶杆图2 夹紧机构结构示意图
1.3 结构设计
根据夹紧机构的工作原理,并结合制动蹄实际尺寸,所设计限位圈厚度为1 mm,高度为24 mm,周长为615 mm,材料选用45号钢,许用应力为235 MPa。根据实际机构运动过程中夹紧滑块与制动蹄的运动行程,夹紧弹簧的最大压缩量设计为5 mm,并结合夹紧机构夹紧力要求,夹紧弹簧的材料选取弹簧钢30W4Cr2VA,弹簧中径、弹簧丝直径分别设计为20、3 mm,夹紧弹簧的实际压缩量确定为4.75 mm。
此外,楔块3作为机构中的重要施力构件,其形状尺寸对整个机构的运动情况会产生较大的影响。楔块的受力分析如图3所示。
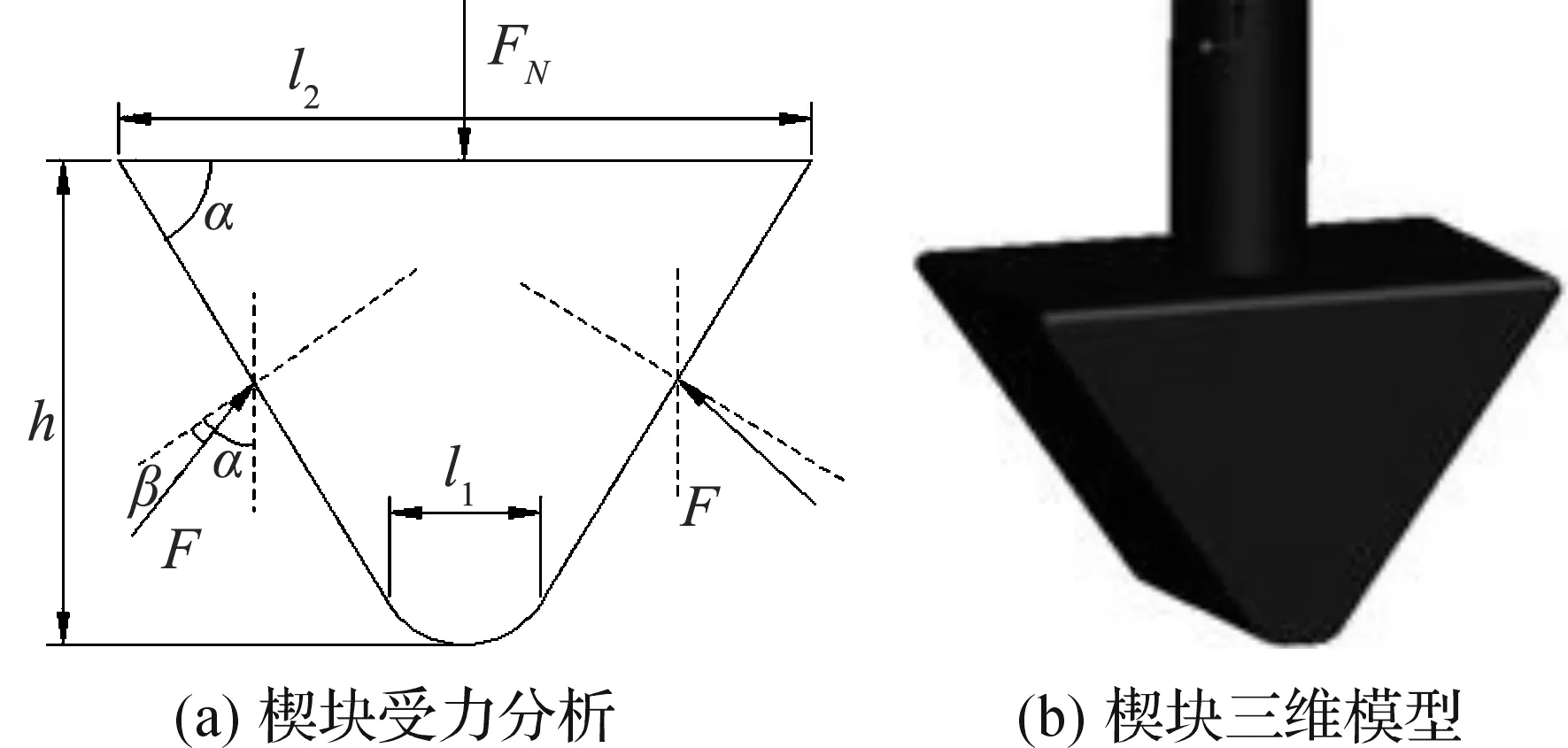
图3 楔块受力分析图和楔块三维模型
(1)
F1=F sin (α-β)
(2)
其中:FN为楔块受到来自夹紧凸轮推杆的压力;F为楔块来自夹紧滑块的压力;β为摩擦角;α为楔块底角;F1为楔块对夹紧滑块的水平压力。
从式(1)、式(2)可知:
FN=2F1cot (α-β)
(3)
由式(3)可知,在F1需满足一定要求的前提下,FN的大小与楔块底角α成反比。同时楔块自锁条件为:α≤β。
综合考虑楔块底角α、夹紧滑块的行程、楔块高度的相互影响,本文设计的夹紧机构有关参数定为:楔块设计为尖端长度l1为10 mm,长端长度l2为70 mm,高度h为50 mm,宽度l3为50 mm。为方便楔块与夹紧滑块接触,楔块尖端倒圆角R为10 mm。楔块的材料选取为20号钢,渗碳淬火达到HRC 58-62。
为避免楔块与夹具之间发生干涉,并且考虑凸轮低速轻载的工况以及凸轮允许的最大压力角等因素,本文将凸轮基圆定为80 mm,推程相应凸轮转角定为25°,回程相应凸轮转角定为75°,松开凸轮顶杆推程定为48 mm,夹紧凸轮顶杆推程定为42 mm。
2 夹紧机构运动分析
利用ADAMS软件对单排夹紧机构运动进行仿真分析,研究各运动件在不同速度下夹具夹紧的作用效果。
2.1 夹紧机构运动学仿真分析
由于仿真初始位置已确定,对凸轮以及传输带添加不同运动速度时,为从理论上避免楔块与限位圈,松开顶杆与限位圈发生干涉,每次仿真都对凸轮与传输带之间的相位差进行修改,凸轮的运动设置为阶跃函数,以便于凸轮与传输带之间设置一个良好的相位差。
2.1.1 凸轮转速对机构运动的影响
根据机构工作原理,夹紧滑块在整个运动过程中,速度和加速度均存在两个波动峰值。第一个出现在机构夹紧过程中:夹紧滑块在楔块的推动下,向两端运动;第二个则出现于机构自动松开过程:松开凸轮顶杆顶开保压滑块后,夹紧滑块在夹紧弹簧的作用下回到初始位置。
当凸轮转速分别为5.5、6.0 r/min以及6.5 r/min,传输带速度设定为1.1 m/min时,夹紧滑块速度和加速度的变化情况如图4、图5所示。由图可知:无论是夹紧过程还是松开过程,随着凸轮转速的增大,夹紧滑块运动速度峰值呈先增大后减小的趋势,凸轮转速越大,夹紧滑块速度达到峰值的时间越短;同样地,凸轮转速越大,夹紧滑块的加速度峰值也越大,达到峰值的时间越短。
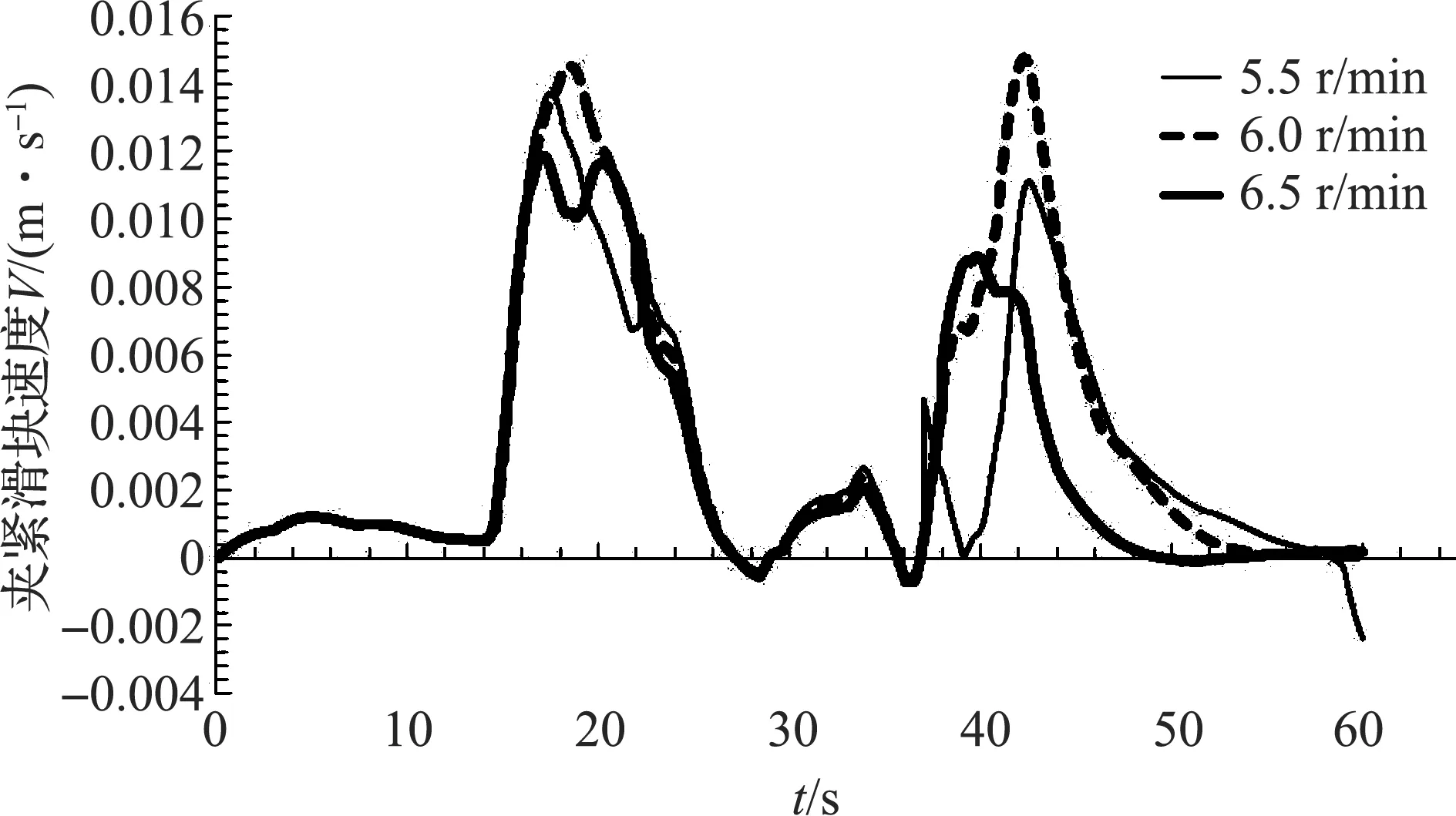
图4 凸轮转速对夹紧滑块运动速度影响曲线
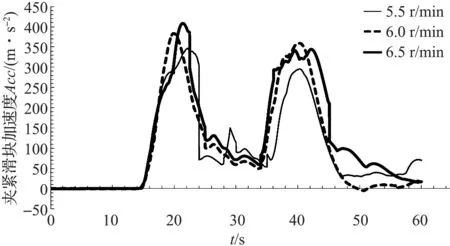
图5 凸轮转速对夹紧滑块运动加速度影响曲线
2.1.2 传输带速度对机构运动的影响
当传输带速度分别为1.1、1.3 m/min以及1.5 m/min,凸轮转速为6.5 r/min时,夹紧滑块速度以及加速度的变化情况如图6、图7所示。
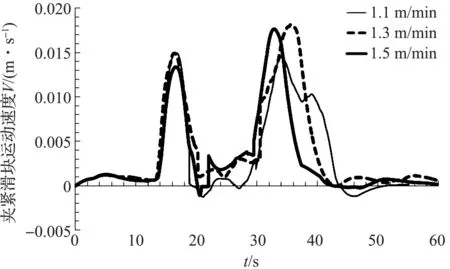
图6 传输带速度对夹紧滑块运动速度影响曲线
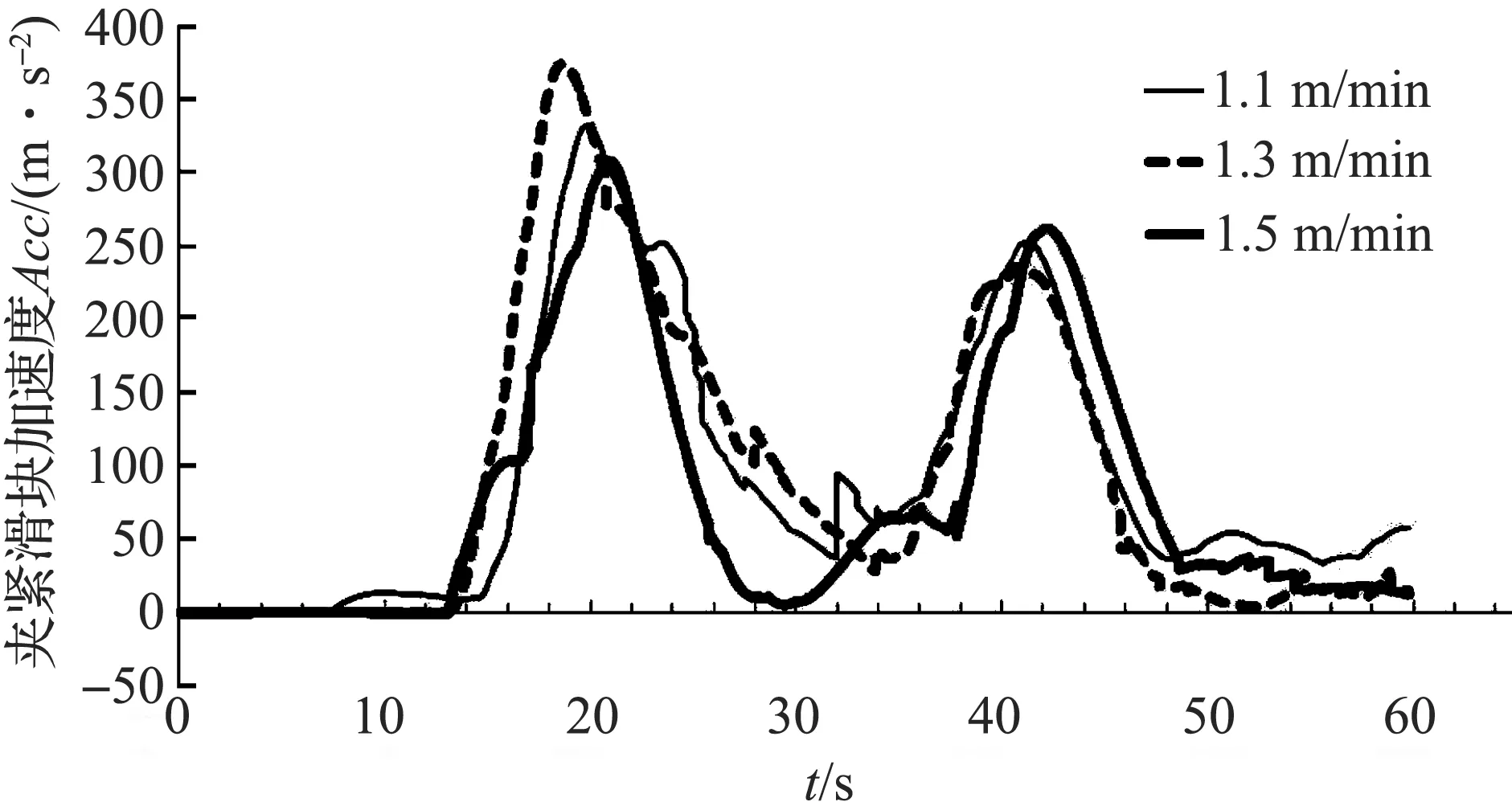
图7 传输带速度对夹紧滑块运动加速度影响曲线
由图6、图7分析可得:当传输带速度为1.3 m/min时,夹紧过程中夹紧滑块运动加速度最大,反映到速度变化曲线,则表现为速度峰值最大;而在松开过程中,不同传输带速度下,夹紧滑块的加速度变化曲线较接近,只是达到峰值的时间存在差别,反映到图6上,则表现为不同传输带速度下,夹紧滑块运动速度相近。
2.2 夹紧机构动力学分析
2.2.1 凸轮转速对机构受力的影响
当传输带速度为1.1 m/min时,凸轮转速分别取5.5、6.0 r/min以及6.5 r/min时,夹紧力的变化趋势如图8所示。由图8分析可知,在不同凸轮转速下,制动蹄受到的夹紧力在80~100 N范围内波动,这说明本文所设计的夹紧机构基本符合预期。
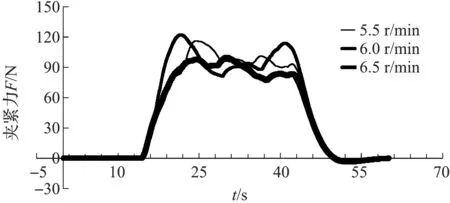
图8 凸轮转速对夹紧力影响曲线
图9、图10分别为不同凸轮转速下楔块斜面法向以及切向作用力的变化情况。由图9可知,随凸轮转速的升高,楔块斜面沿法线方向受力增大。由图10可知,随凸轮转速的升高,楔块斜面沿切线方向受力反而减小。
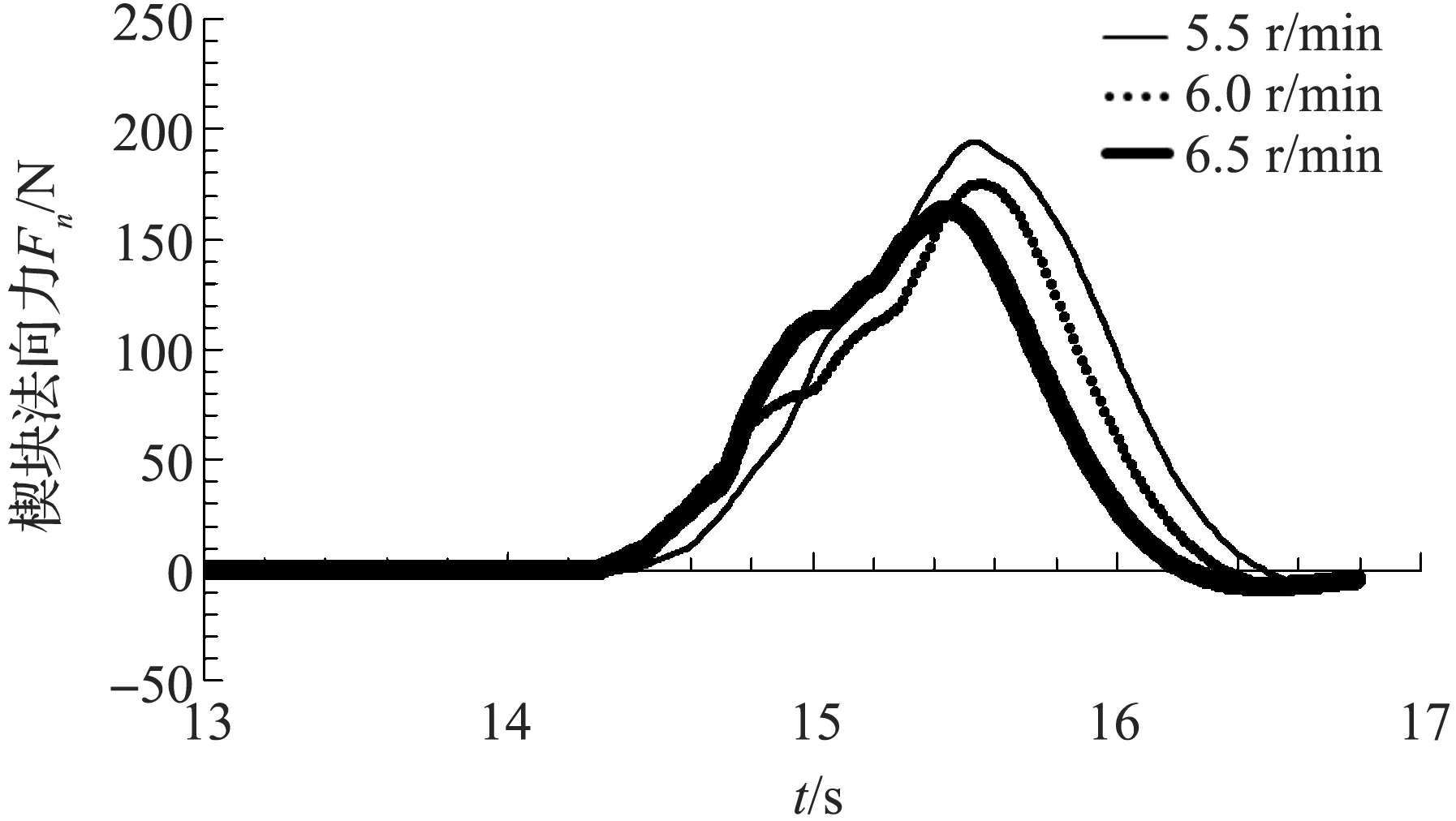
图9 凸轮转速对楔块斜面法向力的影响曲线
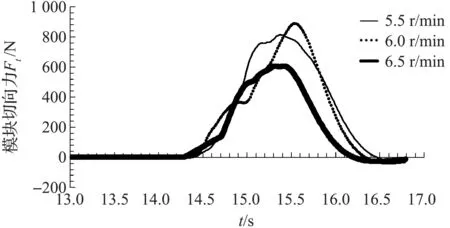
图10 凸轮转速对楔块斜面切向力的影响曲线
2.2.2 传输带速度对机构受力的影响
为研究传输带速度对夹紧力以及夹紧滑块与楔块之间的作用力的影响,取凸轮转速6.5 r/min,传输带速度分别取1.1、1.3 m/min及1.5 m/min的情况进行分析。传输带速度对夹紧力的影响曲线、对楔块斜面法向力和斜面切向力的影响曲线分别见图11-图13。
由图11可知,三种传输带速度下,制动蹄所受的夹紧力变化曲线较为接近,表明传输带速度对制动蹄受到的夹紧力不产生显著的影响,结合图8说明所设计的夹紧机构能够在不同工况下保证夹紧力的稳定。
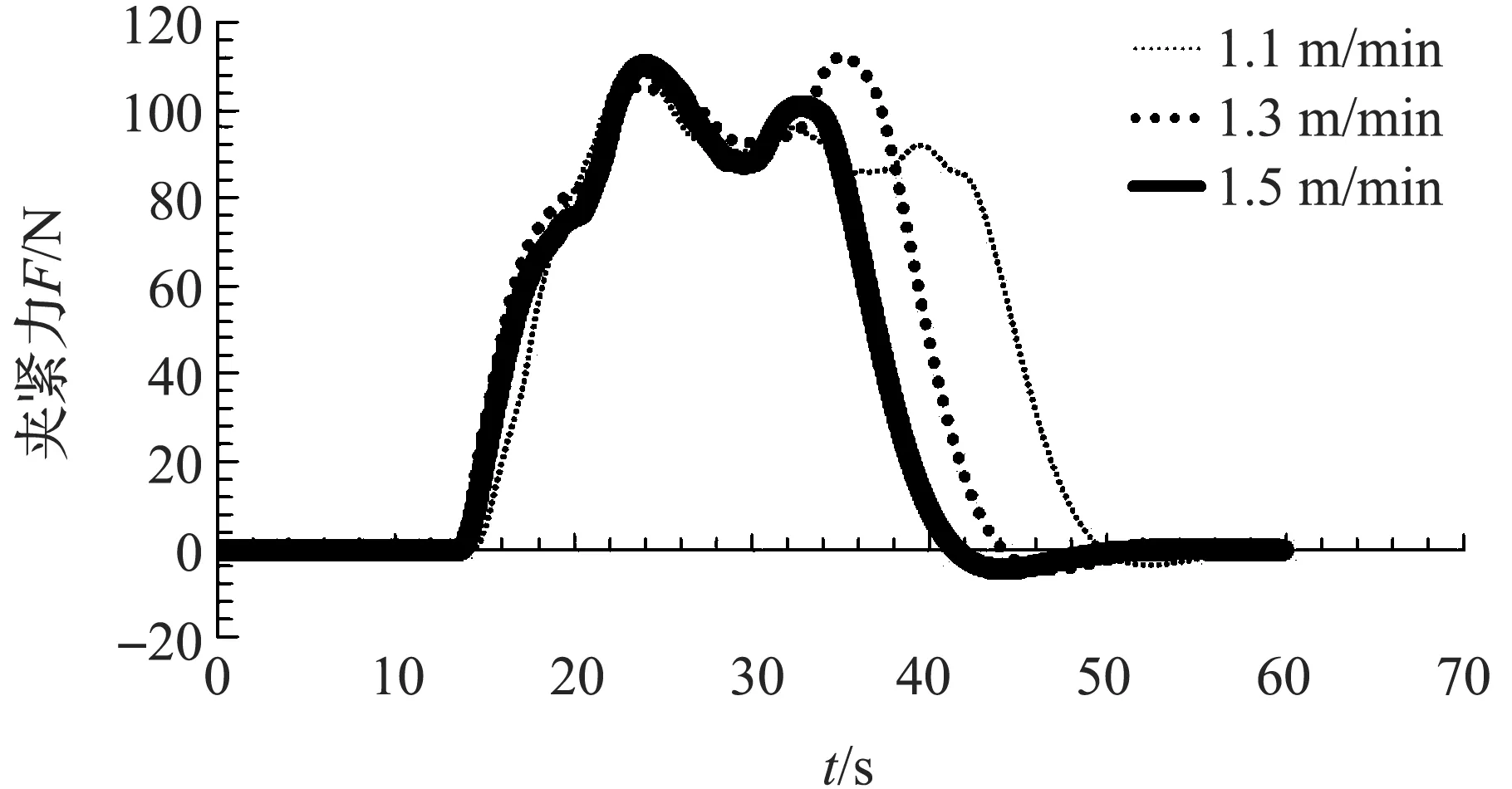
图11 传输带速度对夹紧力的影响曲线
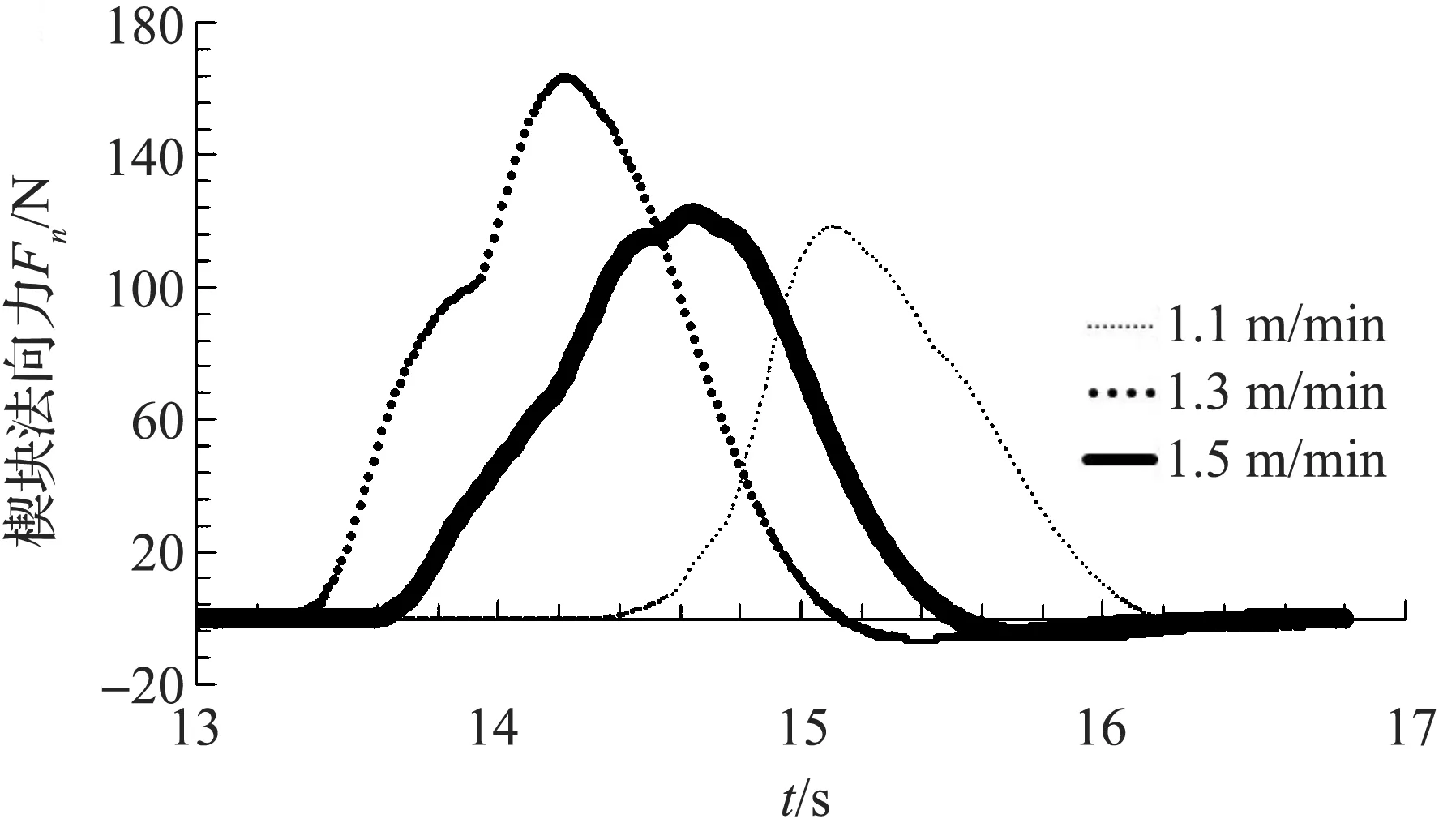
图12 传输带速度对楔块斜面法向力的影响曲线
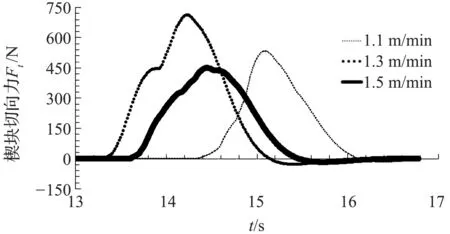
图13 传输带速度对楔块斜面切向力的影响曲线
由图12可知,楔块受到的沿斜面法线方向的作用力随传输带速度增大有着先变大后变小的规律。由图13可知,楔块受到的沿斜面切线方向的作用力随传输带速度的增大,先增大后减小。
通过对夹紧机构进行动力学分析,可以发现该夹紧机构在不同工况下,夹紧力均能够维持在80N左右,且楔块与夹紧滑块之间受力相对稳定,结合运动学分析,验证了该夹紧机构理论上的合理性。
3 热-结构耦合分析
夹紧后的制动蹄需进保温箱进行热处理,由于各材料的热膨胀系数和导热系数不同,在高温下产生不同变形,进而影响压紧力,因此需对夹紧机构进行热-结构耦合分析[11-13]。
3.1 有限元分析模型
本文设计的夹具模型结构对称,故选取一半结构进行分析。图14(a)—(d)分别为限位圈、摩擦片、摩擦片与蹄形铝片接触对、弹簧-滑块的有限元网格。限位钢圈主要承受摩擦片的作用力,在内部产生张力,钢圈的长度和宽度远远大于厚度,近似认为是板壳结构,采用壳单元。制动蹄片包括蹄形铝片和摩擦片,采用四面体单元划分网格,两者之间建立接触对。弹簧和滑块之间建立两个接触对,全部采用四面体划分网格。材料属性见表1。
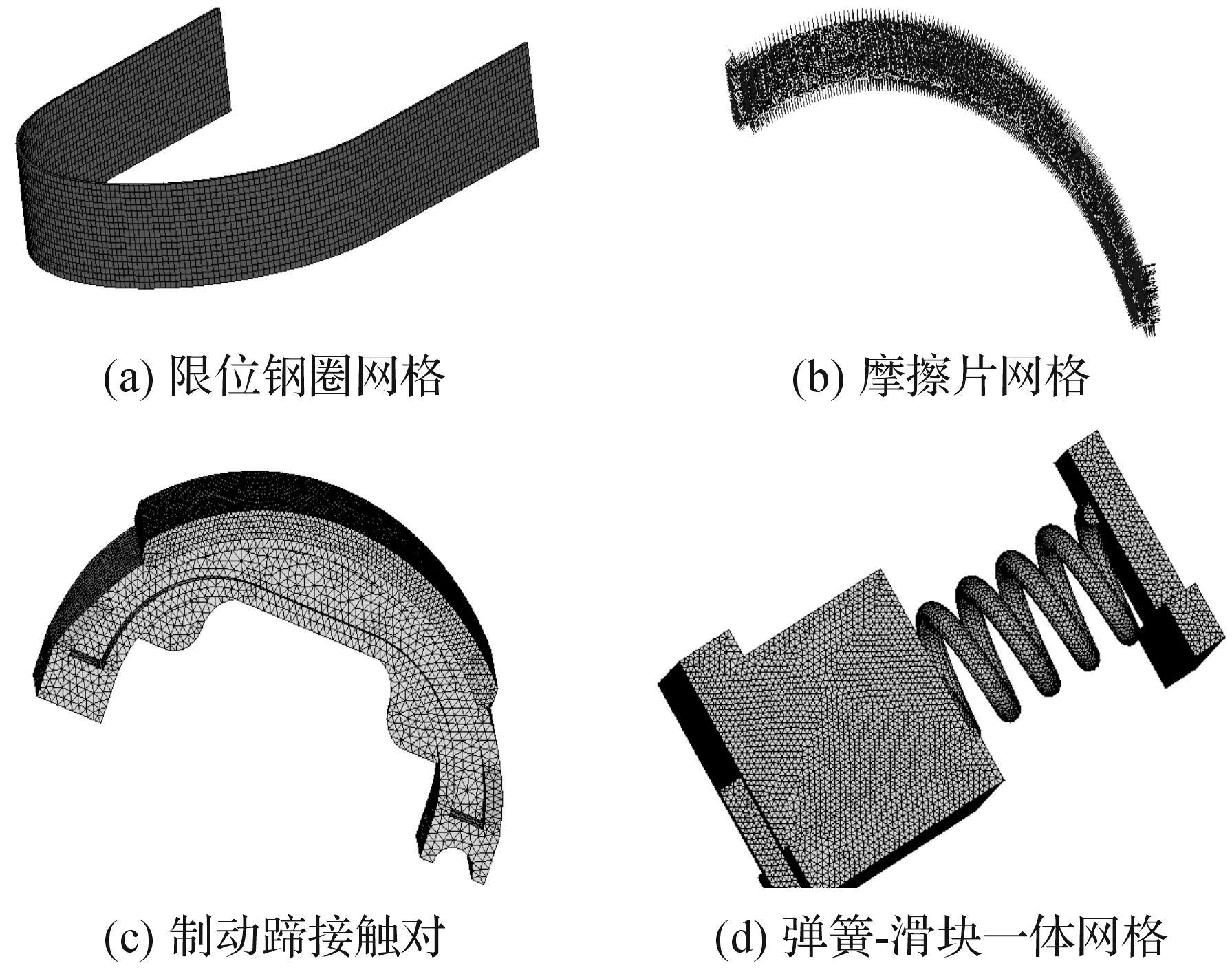
图14 网格划分

属性弹性模量/GPa泊松比密度/(kg·m-3)比热容/(J/(kg·℃))线膨胀系数导热系数/(W·(m·K)-1)钢带2110.3078504601.92×10-550弹簧/滑块1930.3078004201.93×10-546摩擦片(石棉)280.3539606001.21×10-548制动衬铁(铝合金)69.50.3027009402.36×10-5188
3.2 静力学分析
对结构进行静力学分析[14-15],添加如下边界条件:固定钢带截面的节点,仅空余制动衬铁及其摩擦片中心部位的若干节点的Z方向(沿压紧力方向)自由度,在夹紧滑块上施加80 N的节点集中力,同时仅保留Z方向的自由度。
由静力学分析结果可知,应力最大值出现在限位圈上,为6.5 MPa左右,夹紧滑块沿压紧力方向的位移量为0.5 mm,如图15所示。

图15 夹紧滑块位移
3.3 结构-热耦合分析
本实验模型采用间接耦合分析[16-17],需先后添加结构和温度边界条件:
a)结构边界条件。结构-热耦合分析的结构边界条件与作静力学分析时添加的边界条件一致。
b)温度边界条件。在80 N压力的作用下,夹具以及工件将产生一定的应力场,转换单元后,对模型整体进行温升加载,求解前的温度设置为20 ℃,加载温度函数T为:T=20*TIME,TIME表示仿真时间,求解时间设定为10 s。
在保温箱内,固体与空气之间存在着传热,传热系数如表2所示。
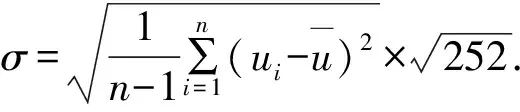
表2 传热系数
图16(a)-(d)分别为时间0.5、5.0、200.0、500.0 s时温度场云图。比较热-结构耦合分析[18-19](图17)与静态结构分析(图15)的结果可以发现,耦合状态下,夹紧滑块位移量相较于静态结构状态增加0.7 mm,同时,由于分析过程中钢带截面节点固定,可知夹紧弹簧的压缩量相应的增加0.7 mm,制动蹄上摩擦片与蹄形铝片之间的夹紧力增大11.6 N,比设计值增大14.5%,表明受热后制动蹄受到的夹紧力增大。
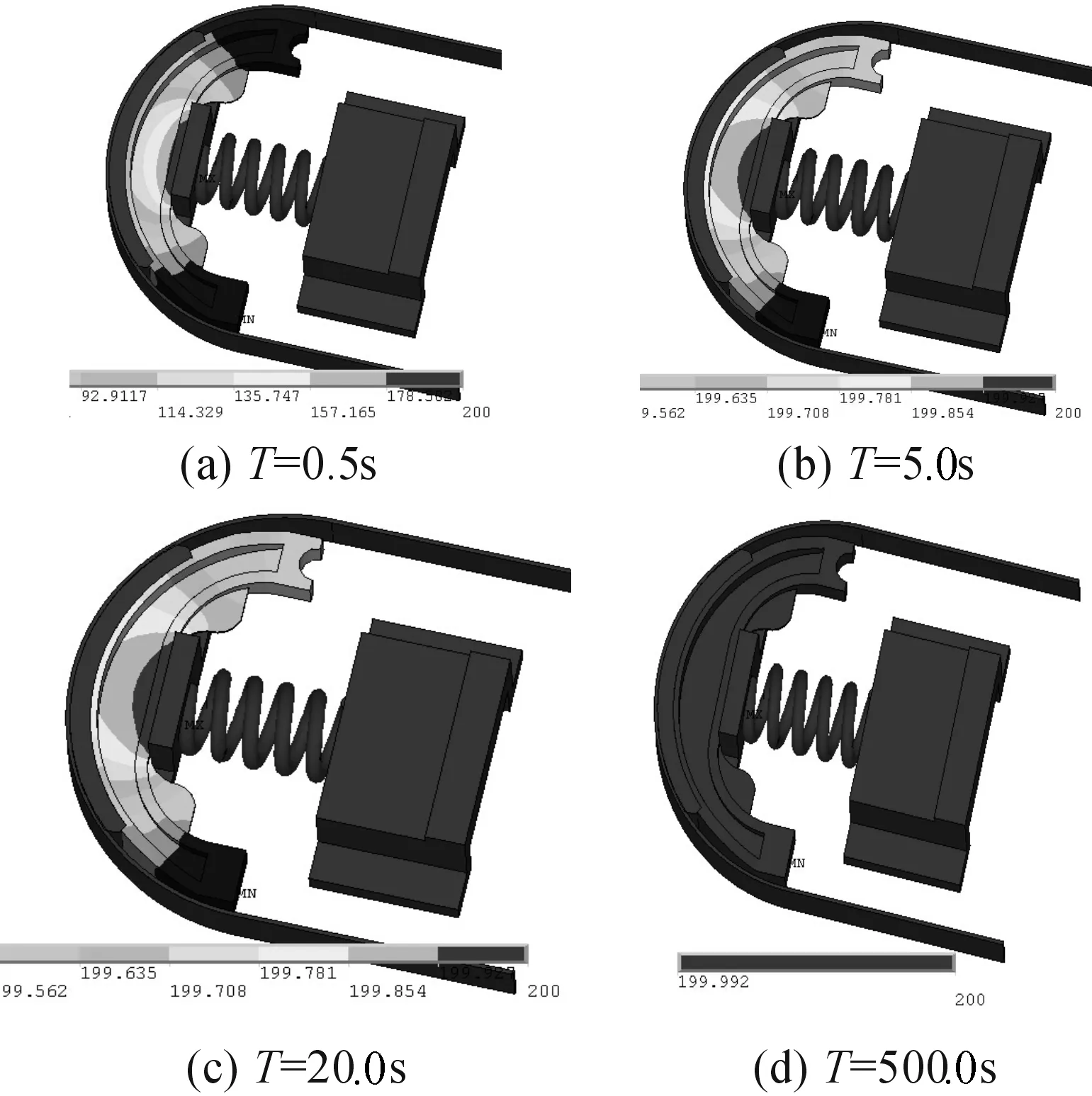
图16 夹具温度场
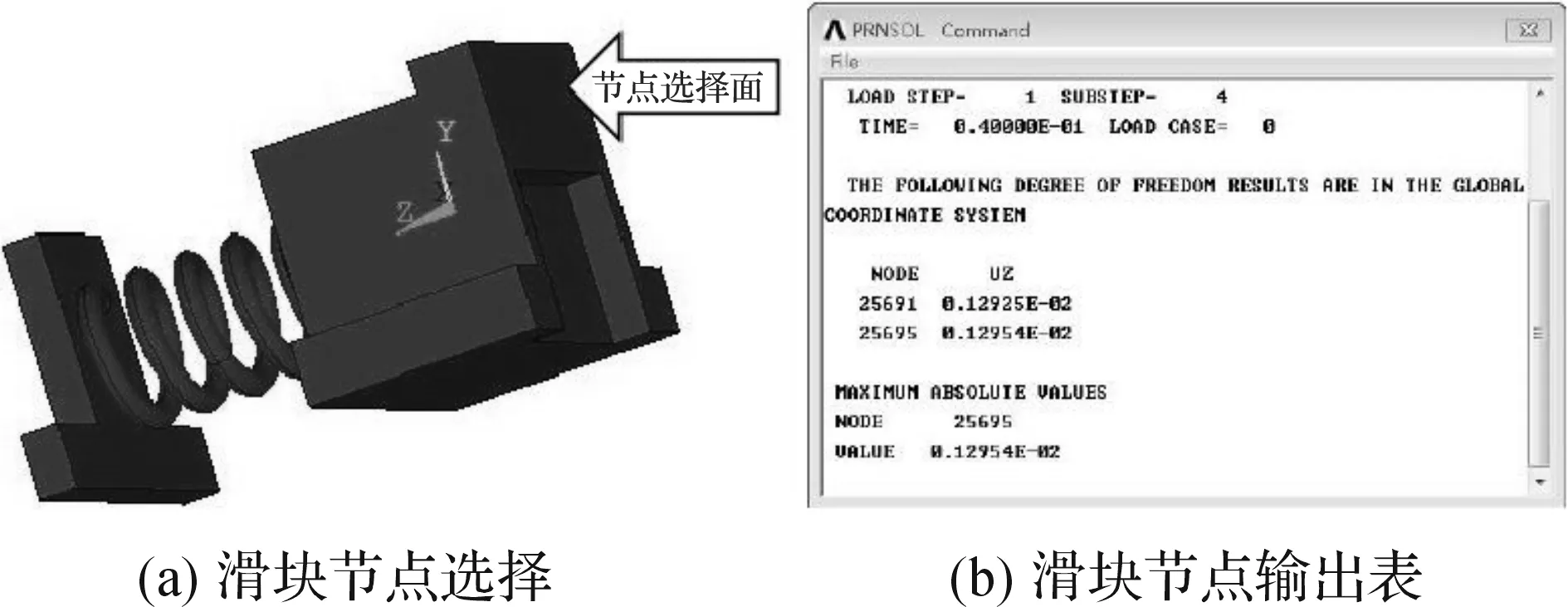
图17 热-结构耦合分析夹紧滑块位移量
由于本文设计夹紧机构的松开动作是通过松开凸轮顶杆顶开保压滑块,夹紧滑块在弹簧作用下回位,而且在初始状态下,弹簧底座与摩擦片之间留有足够的间隙,因此无论夹紧力是否有变化,均能保证制动蹄片与夹具松开。
4 结 论
本文根据摩托车制动蹄的生产要求,提出一种了凸轮滑块夹紧机构,设计了关键部件;对夹紧机构进行运动学和动力学仿真,分析了不同的凸轮转速和传输带速度对机构夹紧力的影响。
通过ANSYS软件对夹紧机构进行结构静力学分析发现,夹紧机构应力主要集中在弹簧和限位钢带弧形处。通过对比静力学分析和热-结构耦合分析结果,发现在200 ℃环境下,摩擦片与蹄形铝块间的压紧力增大14.5%,达到91.6 N。
由于夹紧机构的结构特点,高温所引起夹紧力的变化不会影响夹紧机构的正常松开,且不会引起夹紧误差积累,因此本文设计的凸轮滑块夹紧机构能满足夹紧机构在涂胶流水线上的工作要求。
[1] 贺吉凡.制动蹄上摩擦片的粘结[J].摩托车信息,2006,22(2):25-25.
[2] 刘凡.基于AD-TRIZ快速夹紧机构创新设计[D].苏州:苏州大学,2013:8-16.
[3] 刘少岗,郑力.虎钳夹紧下工件定位稳定性的快速算法[J].现代制造工程,2004(2):79-80.
[4] 秦国华,张卫红,周孝伦.夹紧方案的数学建模及夹紧力的优化设计[J].机械科学与技术,2005,24(4):438-442.
[5] 李涵武,杜宏磊,赵雨旸.汽车鼓式制动器制动鼓的热-结构耦合分析[J].林业机械与木工设备,2011,39(7):25-27.
[6] 包圳,苏小平,张桃沙.汽车鼓式制动器热结构耦合分析与仿真[J].机械设计与制造,2015(8):189-192.
[7] 齐先坤,邵忍平,汪亚运.基于UG与ANSYS Workbench的齿轮箱体热-结构耦合分析研究[J].机械传动,2015,39(6):16-19.
[8] 杨淑贞,董彬.基于Workbench的行星齿轮组热-结构耦合分析[J].制造业自动化,2015,37(6):75-76.
[9] 梅益,王方平,刘乔英.重载减速箱有限元热-结构耦合分析研究[J].煤矿机械,2011,32(8):58-60.
[10] 李昱霖,刘莉,龙腾,等.高速飞行器气动热结构耦合分析及优化设计[J].弹箭与制导学报,2014,34(5):138-143.
[11] 赵凯辉,魏朗.鼓式制动器三维热-机耦合温度场仿真[J].农业机械学报,2009,40(2):32-36.
[12] 杨智勇,韩建民,李卫京,等.制动盘制动过程的热-机耦合仿真[J].机械工程学报,2010,46(2):88-92.
[13] 黄健萌,高诚辉,唐旭晟,等.盘式制动器热-结构耦合的数值建模与分析[J].机械工程学报,2008,44(2):145-151.
[14] TIROVIC M, SERGENT N, CAMPBELL J, et al. Structural analysis of a commercial vehicle disc brake caliper[J]. Proceedings of the Institution of Mechanical Engineers: Part D: Journal of Automobile Engineering,2012,226(5):613-622.
[15] YELDIZ Y, DUZGUN M. Stress analysis of ventilated brake discs using the finite element method[J]. International Journal of Automotive Technology,2010,11(1):133-138.
[16] 阎彬.结构-热耦合问题及结构疲劳的可靠性分析方法研究[D].西安:西安电子科技大学,2013:17-19.
[17] 张洪才.ANSYS 14.0理论解析与工程应用实例[M].北京:机械工业出版社,2013:433-453.
[18] CHOI J H, LEE I. Transient thermoelastic analysis of disk brake in frictional contact[J]. Journal of Thermal Stresses,2003,26(3):223-244.
[19] CHOI J H, LEE I. Finite element analysis of transient thermoelastic behaviors in disk brake[J]. Wear,2004,257(1/2):47-58.
(责任编辑: 康 锋)
Design of Cam-Slider Clamping Mechanism and Thermal-Structure Coupling Analysis
ZHURong,YUYaxin,ZHOUZhidong,LIULei
(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)
To meet the requirements of the automated production of motorcycle brake block, clamp the friction plate and horseshoe-shaped aluminum block and maintain pressure under high temperature, a kind of cam-slider clamping apparatus was designed in this paper, maintaining pressure between friction plate and brake block. The effect of cam speed and transmission speed on clamping force was gained through simulated analysis analyzed of different operational speed on the clamping force, through kinematics and dynamics simulation of clamping mechanism. Coupling analysis of temperature field and stress field was conducted in the thermal insulation box for the brake block in clamping state to gain the displacement changes of clamping mechanism and work piece. Thermal-structural coupling analysis of the clamping apparatus was conducted to analyze the change in displacement of the various components of the clamping mechanism, with the help of the finite element software, in the incubator. The results of the simulation demonstrate that the displacement of the slider in the thermal-structural coupling state was 0.7 mm larger than that in the normal temperature structural state, and leading clamping force to increase by 11.6 N. Owing to the special structural characteristics of clamping mechanism, the change of clamping force will not affect normal loosening of clamping mechanism, so this kind of clamping mechanism, in the paper, can release normally in spite of the change of clamping force, thus working properly meet working requirements under high temperature environment.
clamping mechanism; brake block; motion simulation; thermal-structure coupling
10.3969/j.issn.1673-3851.2017.01.007
2016-06-21
日期:2017-01-03
国家自然科学基金项目(51475430);浙江理工大学521人才培养计划项目;浙江理工大学科研创新团队专项项目
竺 熔(1991-),男,浙江宁波人,硕士研究生,主要从事农业机械设计与分析方面的研究。
俞亚新, E-mail:yyxin@zstu.edu.cn
TH112;TH113
A
1673- 3851 (2017) 01- 0035- 07

