多伦县降雨量时间序列的随机模拟

李睿芳

(天津师范大学，天津 300380)



多伦县降雨量时间序列的随机模拟

李睿芳

(天津师范大学，天津 300380)

以1971～2002年的降雨量资料为依据，利用相关知识和时间序列分析方法,对多伦县降雨量时间序列进行了模拟。利用年资料建立随机模型，根据时间序列的自相关系数和偏相关系数的比较建立了一阶平稳的AR(1)模型。 通过模型模拟出了服从偏态分布的降雨量序列,并通过误差分析得出了由AR(1)模型模拟的大量序列都较符合预报要求，故此模型在实际中可以对水文时间序列进行偏态模拟。

AR(1)模型； 水文时间序列； 自相关系数； 偏相关系数

1 引言

依据观测到的多伦县降雨量样本序列建立随机水文模型，由模型模拟出大量降雨量序列。虽然在水文随机模拟中还存在一些问题有待解决，如模型与参数的不确定性的影响，但水文随机模拟技术的正确使用，将有助于在水资源工程的规划设计和管理运用中得到比应用传统方法更为可靠的结果，从而可以提高规划设计或管理运用的科学水平。

2 时间序列模型建立

2.1 建模目的

出自模型模拟序列的应用十分广泛，在水文水利计算、水文测验、水文站网规划以及水文预报中均有应用，不同的目的要求有不同的模拟序列即不同的模型，设计建立模型的目的是根据降雨量资料的分析情况，建立随机模型，以便模拟出大量序列。

2.2 模型类型的选择

由自相关图可以看出该序列存在着相依性，为一组相依序列，考虑以下几点初步选用AR(p)模型： ① AR(p)模型表征降雨量序列的统计特性有一定的物理基础； ② AR(p)模型参数的估计可以用简单的距法，而且精度较高； ③ AR(p)模型形式简单，数字处理方法简单，为大家所熟悉。

2.3 模型形式的识别

选定AR(p)模型后，主要问题是如何确定阶数p，对模型识别阶数p的主要方法是对偏相关系数的统计分析。当k≥1时，数据落入容许限内，即可推断出p=1，换言之，据偏相关系数的统计分析，AR(1)模型可以用来描述该降雨量系列的统计变化。

2.4 参数估计

因此对降雨量序列建立AR(1)模型为：

(1)

2.5 利用AIC准则对模型进一步识别

由准则计算的情况如下：

AIC(0)=29Ln(5120.872)+2×0=247.6913

AIC(1)=29Ln(4757.441)+2×1=247.5565

AIC(2)=29Ln(4648.0775)+2×2=248.876

AIC(1,1)=29Ln(4673.811)+2×2=249.04

根据计算结果，设计中采用AR(1)模型。

2.6 模型的检验

利用建立的AR(1)模型和实测的1999年降雨量对2000～2002降雨量进行模拟，AR(1)模型递推公式为：

(2)

利用(2)式递推出2000～2002年降雨量的随机项，加上确定性成分就得到了 2000～2002年降雨量的模拟值。

计算的实测值与模拟值的绝对误差如表1,因绝对误差没有超过2倍标准差,所以模型检验符合要求，即AR(1)模型可用来模拟降雨量序列。

3 模拟降雨量序列

确定出AR(1)模型后，还要判断随机项是属于正态分布还是偏态分布的, 经计算随机项的偏态系数Cs=0.119，因此可以判断该序列属于偏态分布。

AR(1)偏态模型如下。

(3)

笔者选用的是长序列法模拟序列计算统计参数,即由模型模拟出一个很长的模拟序列,然后进根据这个长序列来估计参数。序列的主要数字特征为数学期望函数，方差函数，偏态系数等。

利用计算机电子表格中的数据分析随机数发生器公式，在计算机上直接生成10组长度为1000的(0，1)上均匀分布的随机数，并从中选取1组长度为1000的随机数序列用来进行模拟。

对服从偏态分布的纯随机项的模拟，将均匀随机数作下列变换：

则ζ1，ζ2为相互独立的标准正态分布[N(0,1)]变量。因为该序列属于偏态分布，偏态系数Cs=0.119<0.5，所以采用近似法又称W—H变换法来进行偏态序列模拟，这一方法的实质在于标准正态分布和标准化的皮尔逊Ⅲ型分布之间存在着近似关系

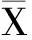
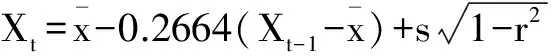
(4)

模拟的步骤如下所示。

(2)由服从标准正态分布的的随机变量的模拟方法模拟出ζ1，算出φ1;

(3)以x0和值φ1代入式(4)又计算出x1;

(4)回到步骤二模拟出ζ2，算出φ2;

(5)以x1,φ2又代入是(4)计算出x2;

(6)重复以上步骤,可得到一个很长的序列，设计中模拟生成长度为1000的序列。在模拟过程中随着模拟长度的增加，模拟序列的统计特性逐渐接近实测序列的统计特性。故模型具有实用性。

(7)考虑到序列的前100项受初值的影响,各将其舍去,最后从剩余序列中选取长度为n的序列。

对于以上步骤可在计算机上算出，用选取的这段模拟序列加上前面分析求得的确定性成分，就得到了降雨量模拟序列。并将实测序列和模拟序列的参数作对比(表2)。

表2 多伦县降雨量实测与模拟序列参数对照

经比较相对误差在允许范围之内(相对误差取10%)，所以选取这段模拟序列符合要求。

4 小结

笔者用随机水文学中的时间序列分析方法和技术，对多伦县1971～1999年降雨量资料进行时间序列分析，建立了一阶平稳的AR(1)模型，通过误差分析，模型模拟的序列较符合要求。

在上述过程中，虽然资料较全面，可靠，但由于随机发生器上产生的随机数随机性较大，因此存在一些不足之处，需要改进，主要表现在以下几个方面。

(1)设计中用随机水文学中的时间序列分析方法和技术对多伦县1971～2002年的降雨量资料进行时间序列分析，建立AR(1)模型，来进行模型模拟。

(2)在进行周期分析时，由于所选取的样本序列较短，有可能存在伪周期成分，与降雨量总体序列的周期可能会存在一定的偏差造成周期成分计算结果存在一定的误差。

(3)对降雨量时间序列选取模型进行建模，可以看出建立符合要求的模型涉及到基本资料分析、随机理论和方法运用等。实际问题错综复杂，需要对具体情况具体分析，以便达到期望的建模目的。

[1]王立坤,付强,杨广林,等. 季节性周期预测法在建立降雨预报模型中的应用[J].东北农业大学学报 ,2002(1).

[2]陈元芳. 随机模拟中模型与参数不确定性影响的分析[J].河海大学学报(自然科学版) ,2000(1).

[3]陈元芳. 非负自回归模型的提出及估计回归系数的新方法[J].水利水运科学研究 , 1994(Z1).

2016-09-06

李睿芳(1990—)，女，天津师范大学硕士研究生。

P426.61

A

1674-9944(2016)18-0023-02