一种基于发送方身份认证的快速信息安全传输算法
赵 冰,周 华
(中州大学 信息工程学院,河南 郑州 450044)
一种基于发送方身份认证的快速信息安全传输算法
赵 冰,周 华
(中州大学 信息工程学院,河南 郑州 450044)
针对开放通信信道的信息安全问题,采用发送方身份认证(数字签名)的方式,设计了一种类似RSA算法的基于离散对数问题的快速信息安全传输加密算法.通过数值举例演绎了该算法的系统设计(选择私钥和公钥)、加密、信息传输、解密和信息恢复等步骤.理论分析和仿真结果表明,该算法的执行速度比RSA算法快2倍,而所需的指数运算比ElGamal加密算法减少50%.因此,该算法是一个安全的、快速的、确定性的方案.
数字签名;密钥交换;离散对数;发送方身份认证
0 引言
本文介绍了一种类似RSA(Rivest Shamir Adleman)算法的信息安全传输协议.然而,该协议的加密免疫不是基于整数分解算法的计算复杂度.如果基数g在以质数p为模的模运算中是生成元,其密码分析的强度是基于离散对数问题(discrete logarithm problem,DLP)的计算复杂度[1-2].
定义1
q:=(p-1)/2.
(1)
如果q也是质数,则质数p被称为安全质数;对于所有的p≥7都会有q是奇数.
如果p是一个安全质数,则生成元g的计算是一个快速计算的过程.
1 FIST(fast information security transmission)加密算法方案设计
1.1 私钥和公钥
该协议是基于发送方和接收方并行生成私钥的加密机制.
定义2 如果p是一个大于或等于7的安全素数,则
g=p-22,
(2)
g是每个p的生成元.
根据Fermat小定理和等式(1)得出,如果p≥7,则有
gq=(p-22)q=(-1)q2p-1=-1≠1(modp)
(3)
和
g2=(p-22)2=24≠1(modp).
(4)
注1 对每一个整数n,都有
gn=p-22n(modp).
(5)
所有参与方都将使用整型参数p和g.
一方X选择a为密钥,则它的公钥可以计算得到
u=ga=p-22a(modp),
(6)
并且,类似的另一方Y选择b为密钥,则它的公钥可以计算得到
w=gb=p-22b(modp).
(7)
注2 两个私钥必须满足不等式
log4p (8) 否则,入侵者不需考虑离散对数问题DLP的复杂性,就能够从式(6)推导出a和从式(7)推导出b;此外,密钥a和b必须与q不同[3]. 1.2 求幂加密法 1)用户计算共同的私有加密码元 e:=ub=wa(modp); (9) 2)如果e不同于2,q和2q,即 gcd(e,d)=1, (10) 用户计算满足等式(11)的整数d, edmodq=1, (11) d:=eq-2modq; (12) 3)消息m的发送方计算密文(加密) c:=memodp; (13) 4)通过开放的通信信道将密文c送到接收方; 5)接收方计算(解密)得 f:=cdmodp. (14) 注3 用户可以从式(12)得到d(解密). 注4 虽然算式(13)和(14)类似于RSA协议,但是却有两个鲜明的特征:①加密码元e是密钥(不公开的);②模归约不是通过第l个用户的两个大质数私钥的乘积nl=plql计算的,而是通过公钥质数q计算的[4]. 命题1 如果m是模p的二次剩余,则f=m,否则f=p-m. 证明 考虑两种结果:①e和d都是奇数;②e或d或两者都是偶数. 对于结果①,等式(11)和费马大定理表明存在一个偶数k,使得 ed=1+qk, (15) 则 cd=med=m×[m(p-1)/2]k(modp)=m. (16) 对于结果②,由二次剩余的费马大定理和欧拉准则表明存在一个奇数k,使得ed=1+qk;同时 (17) 注5 如果m是模p的二次剩余,则对每个结果都有f=m,否则在式(17)中cd=p-m. 然而,每个明文块m的二次剩余的验证是一个耗时的过程.为了克服这个缺陷,有两个方案可供选择. 方案1 发送方连同密文c一起传送一个二进制指示符R,即0或1;如果m是偶数,则发送方发送0,否则发送1.对于接收方,如果f的奇偶校验值等于R,则m:=f;否则 m:=p-f. (18) 方案1的所有情况都汇总在表1中. 表1 信息恢复案例 e,d信息恢复e和d是奇数f=me和d是偶数f=±mifpar(f)=Rthenm:=felsem:=p-f 方案2 发送方预设条件m和分配v:=2m,并且计算c:=vemodp.如果f=cdmodp是偶数,则m:=f/2;否则 m:=(p-f)/2. (19) 在密码体制系统设计方面,每个用户求幂计算它们的公钥,根据算式进行两次取幂计算出它们的公钥式(6)和式(7)及私有加密码元式(9). 加密时,只需进行一次取幂式(13).类似地,解密时,每个接收方也只执行一次取幂式(14).虽然为了保持高安全级别,需要定期选择新的私钥和重新计算加密码元和解密码元,但是不需要在每个信息块传输时一起发送提示码,因为可以由ElGamal算法完成[5](表2). 表2D和d相对比的实例,p=9 839 e59114333343074567D590387457155549184798769545d9843826223657235603850545D/d6.002.293.209.602.382.281.00 由于本文提出的算法(9)~(14)是基于离散对数DLP的计算复杂度,因此它比基于因子分解的RSA算法具有一定的优势,而且也比ElGamal算法更高效.事实上,在每个数据块安全传输的取幂运算方面,它比数字签名RSA算法快2倍,也比ElGamal算法快1.5倍.另外,ElGamal算法需要多一倍的带宽,因为在传输密文时,它必须与每个加密的块m一同发送一个短暂的公钥{提示}, h:=gxmodp. 如果e是偶数,则有“二进制”移位的概念被提出,e:=e±1.然而,即使加密码元e是奇数,还有另外一个优势,那就是由方程(11)得到解密码元d. 命题1 假设 eDmod(p-1)=1, (20) 并且e是奇数,则 (21) 证明 令ed=1+qk,同时 eD=1+2qk. (22) 则等式(22)表明 e(D-d)=q(2K-k). (23) 由于e和q互质,则等式(23)表明q分为D-d.因此, d=Dord=D-q. (24) 现在,假设D=d+qz,其中z是0或者1,D<2q,则由等式(20)得z<2.因此,如果eD=1+2qK,则e(d+qz)=1+2qK表明 ed=1+q(2K-z). (25) 最后,根据等式(25)分析奇偶性推断:如果d是奇数,则z=0;如果d是偶数,则z=1. 此外,加密码元和解密码元提供了数字签名(发送方的身份认证),它们被用于具体用户(收发双方X和Y)的通信计算. 3.1 比较分析 ElGamal算法只是在私有通信中动态地应用Diffie-Hellman密钥建立方案来隐藏信息的几种建设性方法中的一种.事实上,收发双方都动态地建立一个共同的密钥(加密码元e(m)),然后,反向逆运算得到值d(m)(解密).在ElGamal算法中,发送方通过把信息m和加密码元e(m)相乘的方法将该信息隐藏[6].此外,还有其他方法可选择:不使用乘法,发送方将加密码元e(m)和m相加,或者利用幂值计算.虽然表面上看使用e进行加法或乘法运算似乎比取幂运算更简单,但是分析显示结果却是相反的(表3). 表3 ElGamal,RSA和FIST算法的对比(X发送m给Y) 算法私钥公钥加密传输解密信息恢复数字签名ElGamala,b,x,y,e(m)d(m)p,gu,wh(m)h(m)=gxe(m)=wxc=me(m)modp{c,h(m)}d(m)=hp-1-bf=cdmodpM=f需要3次取幂RSApk,qk,dk,K=1,2,…ek,nk=pkqkcm=f需要4次取幂FISTa,b,e,dp,gu,wc=memodp{c,R}f=cdmodp如果par(f)=R则m=f,否则m=p-f需要2次取幂 3.2 仿真实验 为证明FIST加密算法的性能,笔者进行了仿真实验,该实验的硬件环境为:Intel Core i7 CPU 4.0 GHz,8 GB内存,160 GB硬盘;操作系统为Windows Server;开发工具为C++BUILDER 6 SP4.实验基于C++构建了一个较为完善的数库,分别对ElGamal算法、RSA算法和本文研究的FIST算法进行耗时情况记录,实验结果如表4所示. 表4 3种算法的耗时情况/s 算法第一次第二次第三次平均耗时ElGamal3.1273.3013.0513.159RSA4.3594.6274.0534.346FIST2.1382.3162.0152.156 由表4的数据计算可知,本文设计的FIST算法的效率是RSA算法的2.015倍,是ElGamal算法的1.465倍,说明FIST算法在信息安全传输效率方面确实有一定的提高. 本文提出的FIST加密算法具有以下创新点: 1)安全质数p被作为模,见式(1); 2)提出了一个运算简便、确定性的方法,该方法为所有用户选择了生成元g(质数元素),见式(2); 3)发送方和接收方之间的安全通信加密码元e是私有的,见式(9); 4)明文块m通过求幂运算被隐藏,而不是通过乘法或者其他二进制运算被隐藏; 5)基于等式见等式(11)的确定性计算过程可以为通信双方找到一个共同的解密码元d; 6)为信息恢复提供了两个可选方案:一是发送二进制指示符R,见式(9),二是在每个明文块m加密之前对其进行预处理,见等式(19); 7)即使加密码元e是一个奇数,在许多情况下,使用d进行解密比使用D更快,见式(20)~(24). 通过以上的比较分析和仿真结果证明,发送方身份认证的快速信息安全传输算法FIST是一个运算简便的、快速的、确定性的方案. [1]魏先民.改进的ECC算法在网络信息安全中的研究[J].计算机科学,2013,40(1):136-138. [2]禹勇,李继国,伍玮,等.基于身份签名方案的安全性分析[J].计算机学报,2014,37(5):1025-1029. [3]黄斌,史亮,邓小鸿.一种基于身份的签名方案密码分析与改进[J].计算机工程,2012,38(24):108-110. [4]肖振久,胡驰,陈虹.四素数RSA数字签名算法的研究与实现[J].计算机应用,2013,33(5):1374-1377. [5]曹阳.基于身份的ElGamal多重数字签名方案[J].科技通报,2015,31(5):197-199. [6]冯超,张权,唐朝京.计算可靠的Diffie-Hellman密钥交换协议自动证明[J].通信学报,2011,32(10):118-126. A Fast Information Security Transmission Method Based on Sender Identification ZHAO Bing,ZHOU Hua (CollegeofInformationEngineering,ZhongzhouUniversity,Zhengzhou450044,China) Aiming at the safety problem on open communication channel,a fast information security transmission method is proposed based on discrete logarithm problem by sender identification (digital signature),which is similar to RSA algorithm.The whole steps of the algorithm are deduced by numerical examples,including the system design (selection of private keys and public keys),encryption,information transmission,decryption,and information recovery.The comparative analysis and the simulation results prove that it is twice times faster than the RSA algorithm,and needs 50% fewer exponential operations than the ElGamal encryption algorithm.So the proposed algorithm is a safe,quick and deterministic method. digital signature; key exchange; DLP; sender identification 2016-10-22 河南省高等学校重点计划项目(15A520066);河南省高等学校青年骨干教师资助计划项目(2012GGJS-260) 赵 冰(1972—),男,河南邓州人,中州大学信息工程学院副教授,主要研究方向:信息安全及计算机应用. 10.3969/j.issn.1007-0834.2016.04.003 TP301.5 1007-0834(2016)04-0010-05
Tab.1 The case of information recovery
2 FIST的复杂性分析
Tab.2 The case of contrast betweenDandd,p=9 839
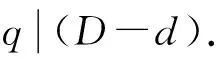

3 比较分析和仿真实验
Tab.3 The contrast of ElGamal,RSA and FIST (XsendsmtoY)
Tab.4 The contrast of time-consuming on three algorithms/s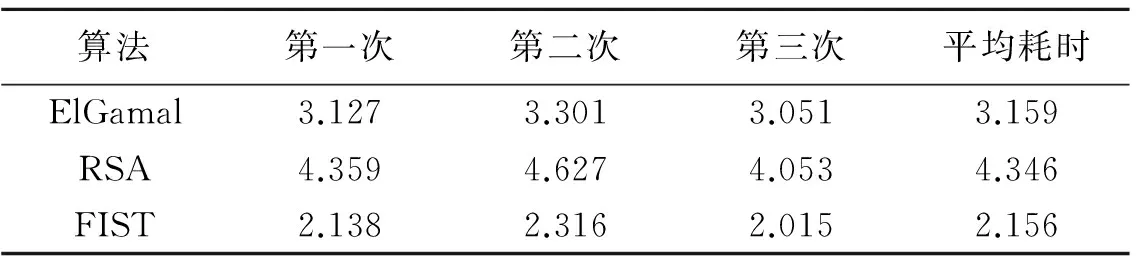
4 创新性和结论

