多重状态时滞系统的min-max鲁棒预测控制

周卫东，郑 兰，廖成毅，蔡佳楠

（1．哈尔滨工程大学自动化学院，黑龙江哈尔滨150001；2．中国船舶及海洋工程设计研究院，上海200011；3．中国电子科技集团公司第三十八研究所，安徽合肥230088）

多重状态时滞系统的min-max鲁棒预测控制

周卫东1，郑 兰1，廖成毅2，蔡佳楠3

（1．哈尔滨工程大学自动化学院，黑龙江哈尔滨150001；2．中国船舶及海洋工程设计研究院，上海200011；3．中国电子科技集团公司第三十八研究所，安徽合肥230088）

针对一类带有扰动、多重状态时滞的凸多面体不确定离散非线性系统，基于预测控制理论提出一种minmax鲁棒预测控制算法。将模型预测控制问题描述为一类无限时域min-max优化问题；采用LMI技术把此问题转变为一类采用LMI描述的约束问题，设计了状态反馈控制器；运用所给信息构造一个改进的Lyapunov-Krasovskii泛函，根据模型预测控制基本原理来求解此优化问题，同时给出了控制器存在的定理及相关证明，进而获得所设计控制器存在的新判据及状态反馈矩阵构造方法，在此基础上给出了鲁棒模型预测控制算法流程。最后，给出了闭环系统渐进鲁棒稳定定理，理论及仿真分析验证了控制器设计的可行性及系统的鲁棒渐近稳定性。

非线性扰动；多重状态时滞；离散非线性系统；状态反馈控制；模型预测控制；线性矩阵不等式

模型预测控制（model predictive controlMPC）具有模型预测、滚动优化和反馈校正三个主要特性。对模型要求低、设计简单、鲁棒性强而且能够有效的处理状态、控制等方面的约束问题，在工业界受到广泛的关注［1］。

在实际生产过程中不确定性与扰动是不可避免且无法预知的，而鲁棒预测控制因其既具备鲁棒控制的优点，可以处理模型的不确定性，又兼具预测控制的滚动优化思想，弥补了经典MPC的不足，因此得到学者们的极大重视［2-8］。文献［2］基于LMI方法给出了一类具有时变时滞、输入约束和扰动的离散系统的控制器设计方法；文献［3］解决了前提不匹配情况下T-S模糊时滞系统的控制器设计问题，该文降低了设计的保守性；文献［4-5］针对具有输入约束的离散时滞系统通过LMI技术研究了一种鲁棒模型预测控制器设计方法，但是在时滞为常数时研究的；文献［6］采用鲁棒预测控制方法研究了一类带有非线性扰动的多重时滞不确定系统的控制律设计问题，但所考虑的系统为连续的；文献［7］解决了一类带有区间时滞的离散非线性系统的预测控制器设计问题；文献［8］研究了一类时滞为多重的不确定离散线性系统的控制器设计方法，所提方法保证了闭环系统的稳定性与可行性。然而，有关多重状态时滞与扰动同时存在的不确定离散非线性系统的鲁棒预测控制问题还有待进一步研究。本文在文献［7-8］的基础上，讨论了一类既具有非线性扰动又同时存在多重状态时滞的不确定离散非线性系统的鲁棒预测控制器设计问题。

1 问题描述与预备知识

记号:Rn为n维欧几里德空间，Rn×m为n×m维实矩阵的集合，In为n×n维单位矩阵。符号∗代表相应的对称块矩阵，即如果H，R是对称矩阵，则

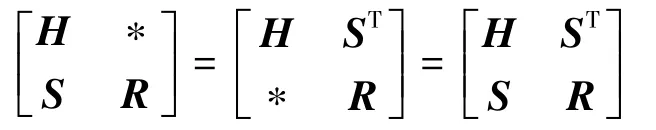
考虑如下一类具有多重状态时滞和非线性扰动的不确定离散非线性系统:

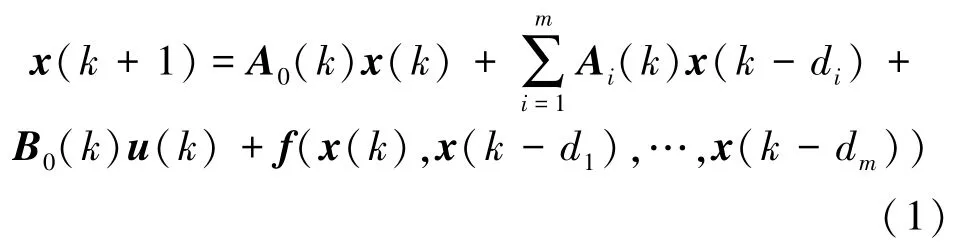
式中:x（k）∈Rnx是系统的状态，u（k）∈Rnu为系统的输入，f（x（k），x（k-d1），…，x（k-dm））是非线性扰动，为方便表述，令fk:=f（x（k），x（k-d1），…，x（k-dm）），且满足:

式中:0＜d1＜…＜dm表示系统的时滞，x（k）= φ（k），-dm≤k≤0是系统的初始条件。系统（1）中的系统矩阵是未知的，并且可以表示成凸组合的形式，即

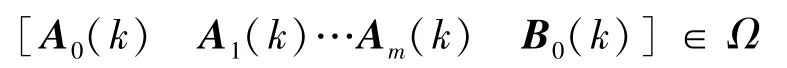
其中

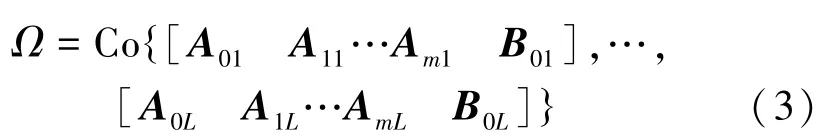
式中:Co表示由L个顶点［A01A11…Am1B01］，…，［A0LA1L…AmLB0L］构成的凸多面体集，即存在L个非负系数0≤λi（k）≤1（i=1，2，…，L），使得

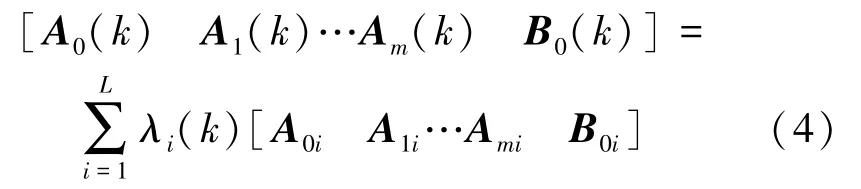
系统（1）的模型预测控制问题可描述为如下问题:设计一种鲁棒预测控制器使所研究系统鲁棒稳定同时获得下面的鲁棒性能指标，即需要考虑如下min-max优化问题:

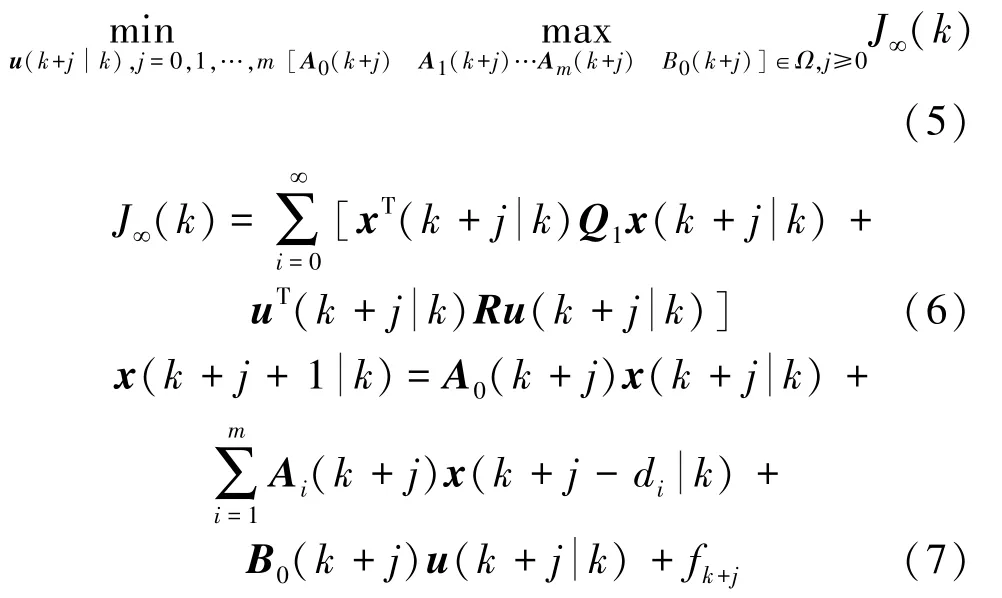
式中:Q1＞0为性能指标中状态的对称加权矩阵，R＞0为控制的对称加权矩阵表示k时刻对k+j时刻输入的预测表示k时刻对k+j时刻状态的预测，并且有

式（6）表示未来控制输入的无限时域和系统预测状态的二次鲁棒性能指标，式（7）表示系统的状态预测模型。

针对系统（1），设计如下的状态反馈控制律:

控制目标:求取所设计控制器中的增益矩阵K，并要求控制输入使得闭环系统渐进稳定。

针对系统（1），构造如下的Lyapunov-Krasovskii函数:

假设在每一个k≥d1时刻是可测量的。在k时刻，假设对所有的［A0（k） A1（k）…Am（k） B（k）］∈Ω，i≥0，有下式成立:

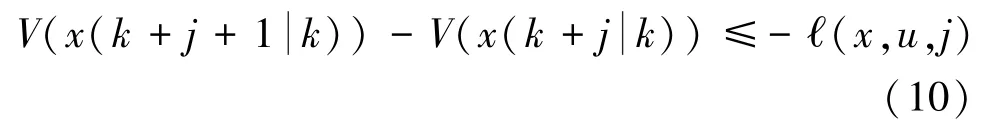
其中

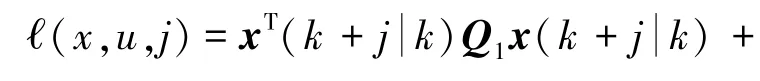
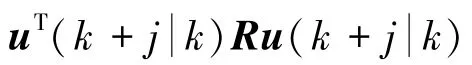
为了使J∞(k)有界，令因此将不等式（10）两边同时从j=0到 j=∞求和，可得

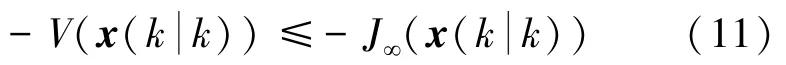
因此:

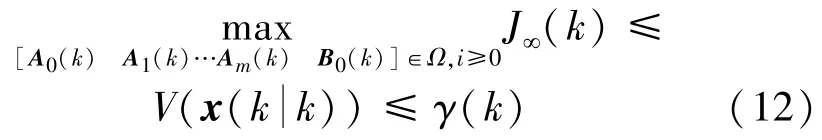
根据本文所需先给出下面的两个引理。

引理1［9］（Schur补）矩阵不等式:

式中:Q( x)=QT(x)，R( x)=RT(x)，S( x)是关于x的仿射函数，则式（13）等价于:1）Q( x)＞0，R( x)-ST(x)Q-1(x)S( x)＞0；2）R( x)＞0，Q( x)-S( x)R-1(x)ST(x)＞0。

引理2［10］设W0(x)和W1(x)都是关于x∈Rn的二次函数，如果对任意的x∈Rn-{0}，有W1(x)＜0，并且存在常数ρ＞0使得

W0(x)-ρW1(x)＜0， x≠0（14）

成立，则有W0(x)＜0。

2 控制器设计及稳定性分析

2．1 基于LMI的模型预测控制器设计

定理1考虑含有延时的离散不确定时滞系统（1），同时令为采样k时刻状态x（k）的测量值。如果存在标量γ（k）＞0，ρ＞0，对称的正定矩阵Q，Qdi，P0，Pd1，…，Pdm和适当维数的矩阵Y满足下述形式的LMI优化问题，那么一定存在状态反馈控制律u满足性能目标（10），其中状态反馈增益K=YQ-1。

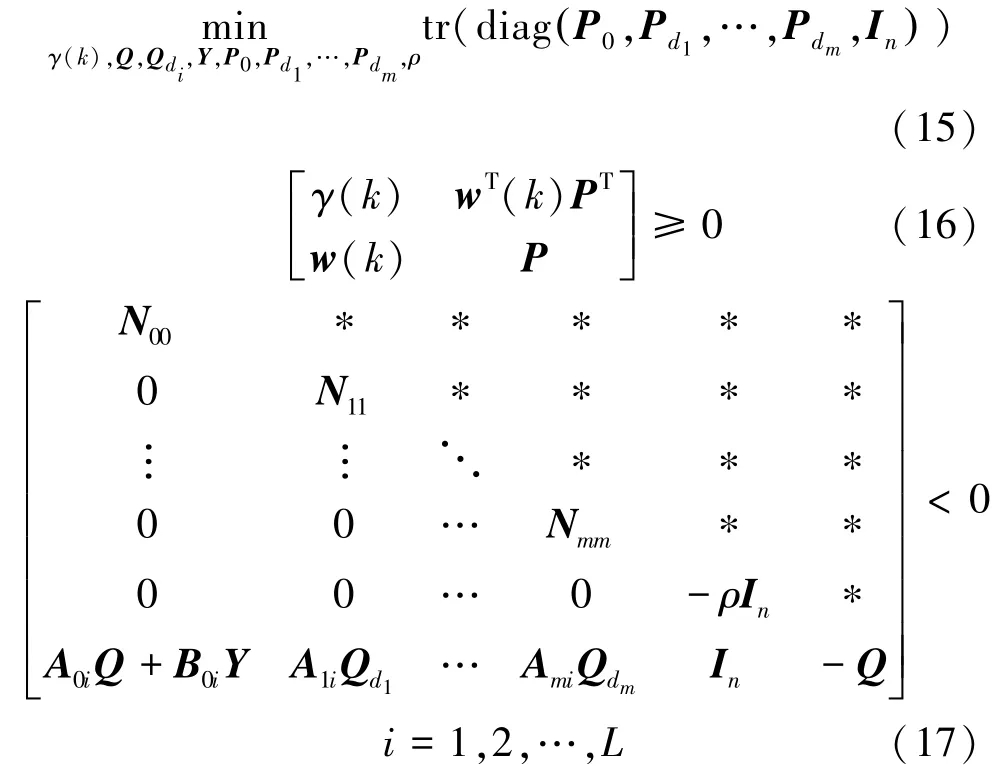
其中

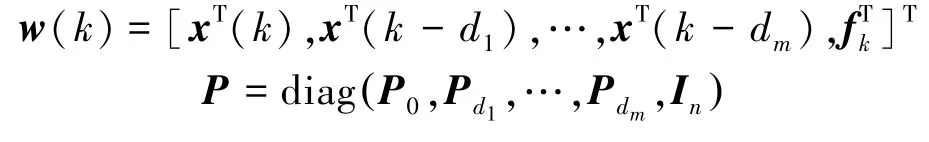
证明:由于式（9）是性能指标的上界，可以通过求解下面的问题把这个界减至最低:

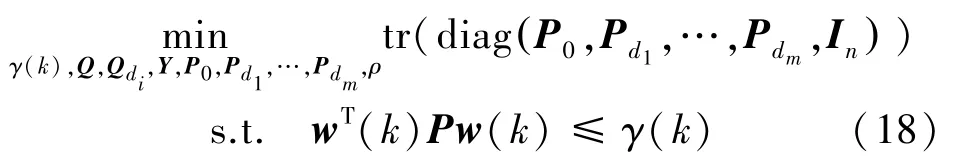
其中，

应用Schur补，式（18）可写为

将式（19）分别左乘和右乘矩阵diag( I，P)，则有

则不等式（16）成立。下面将证明不等式（17）成立。

取Lyapunov-Krasovskii函数（9），对它求差分有

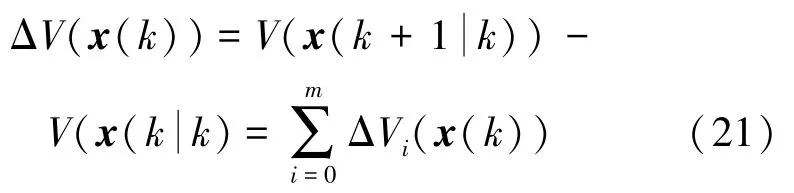
则

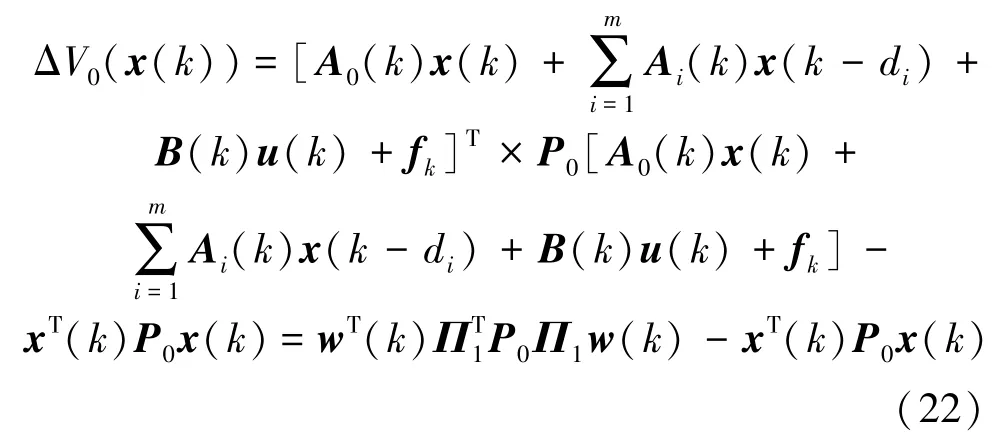
其中

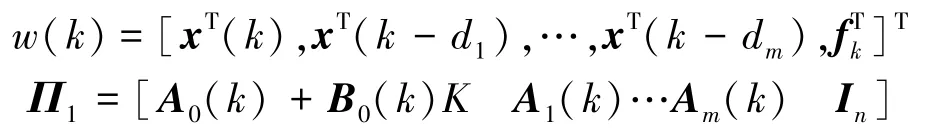
通过计算:

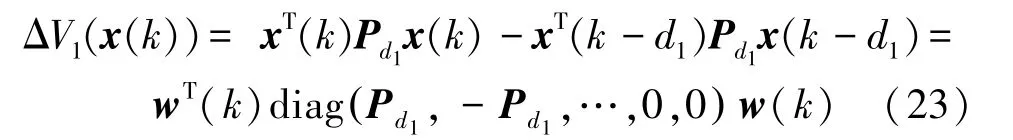
进一步:

把式（22）～（24）代入到式（21），有

其中

考虑式（10）和u（k）=Kx（k），设

其中，Θ2=diag( Pd1-P0+Q1+KTRK，-Pd1，…，-Pdm，0)又因为式（2）可以写成:

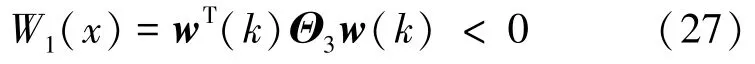
其中

根据引理2，存在数λ＞0使得W0(x)-λW1(x)＜0成立，则W0(x)＜0，即

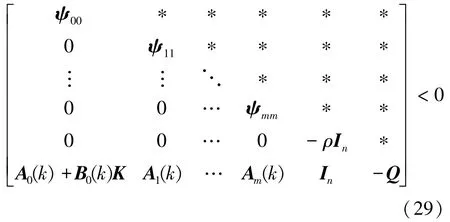
其中

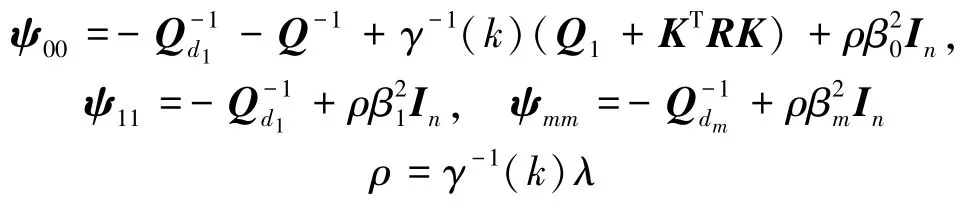
再利用Schur补有

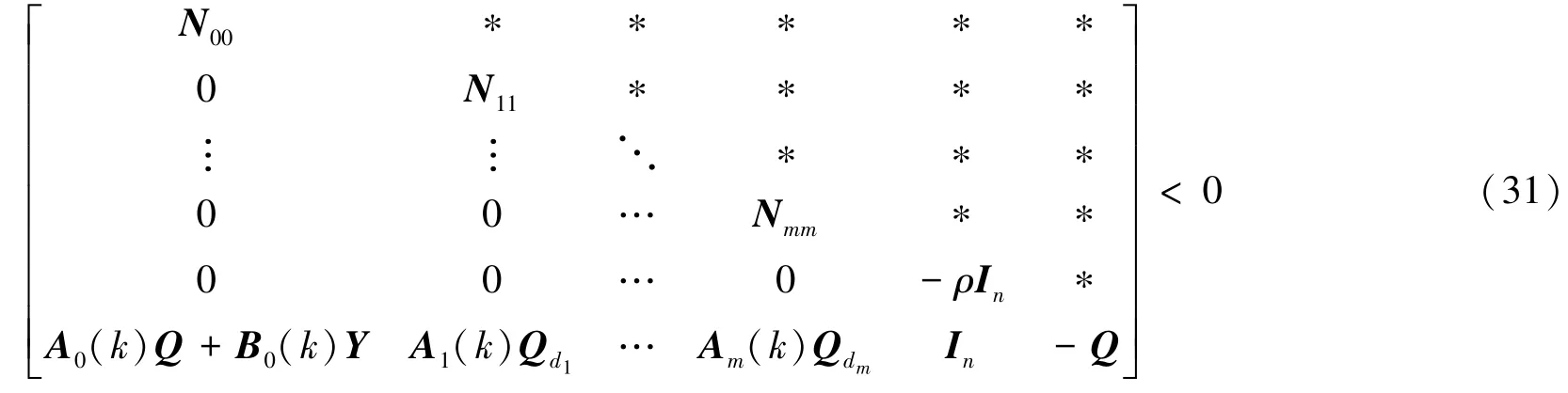
其中

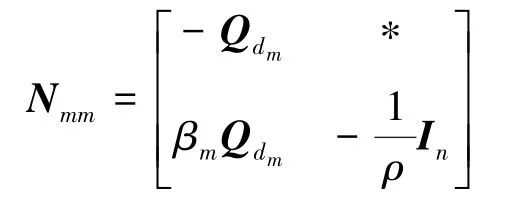
又因为式关于系统矩阵满足［A0（k） A1（k）…Am（k） B（k）］∈Ω，根据凸集的基本性质，式（31）成立当且仅当对凸包Ω的每个顶点都成立，即式（31）成立当且仅当式（17）成立。

2．2 控制算法

综合上面的控制器设计过程，系统（1）的控制算法如下:

1）测量当前时刻系统的状态x（k），并获得过去时刻的状态x（k-1），…，x（k-d1），…，x（k-dm）；

3）选择适当的对称正定矩阵Q1和R；

4）定义优化问题（5）～（7）中的各个变量，标量γ（k）＞0，ρ＞0，正定对称矩阵Q，Qdi，P，Pd1，…，Pdm和适当维数的矩阵Y；

5）用MATLAB中的LMI工具箱求解优化问题（5）～（7），得到最优解γ（k），ρ，Y，Q，Qdi，P0，Pd1，…，Pdm；

6）计算出状态反馈预测控制控制器增益矩阵K=YQ-1；

8）令k=k+1，重复步骤1）～7）。

2．3 可行性与稳定性分析

引理3［11］（可行性） 如果定理1中该优化问题在k时刻是可行的，那么它对所有k+j，j＞0都是可行的。

定理2如果优化问题（5）～（7）在k时刻是可行的，则由定理1给出的状态反馈控制器u（k）= Kx（k）使闭环系统鲁棒渐近稳定。

证明由引理3可知最优化问题（5）～（7）是可行的。所以假设分别表示最优化问题（5）～（7）在k时刻和k+1时刻的最优解，最优状态分别为和

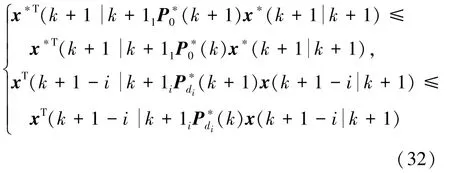
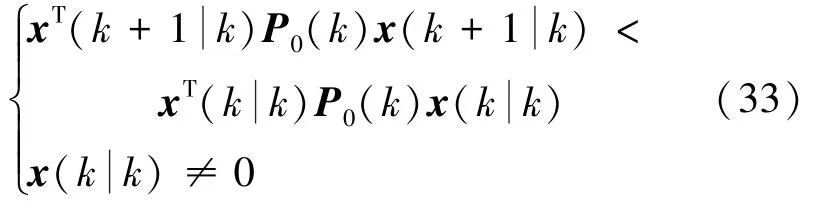
由上述假设可知:

这里i=1，2，…，d1，…，dm。则有

又因为测量状态

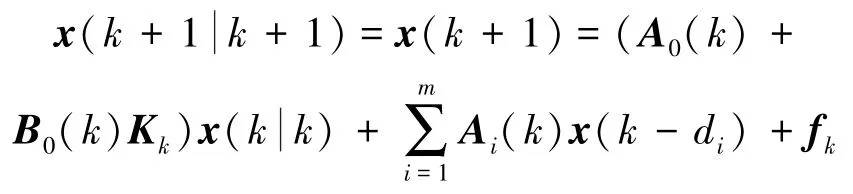
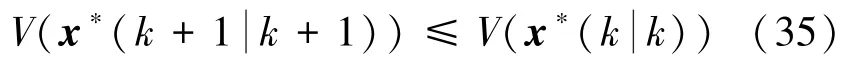
式（35）说明V( k｜k)是单调非增且有界的Lyapunov函数，当k→∞时，有x( k)→0。由离散Lyapunov稳定性理论可以说明闭环系统鲁棒稳定。

3 仿真结果与分析

考虑如下带有非线性扰动、时滞和凸多面体不确定的离散非线性系统:

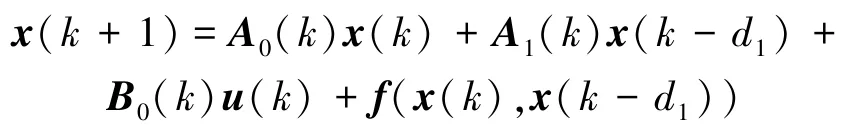
其中

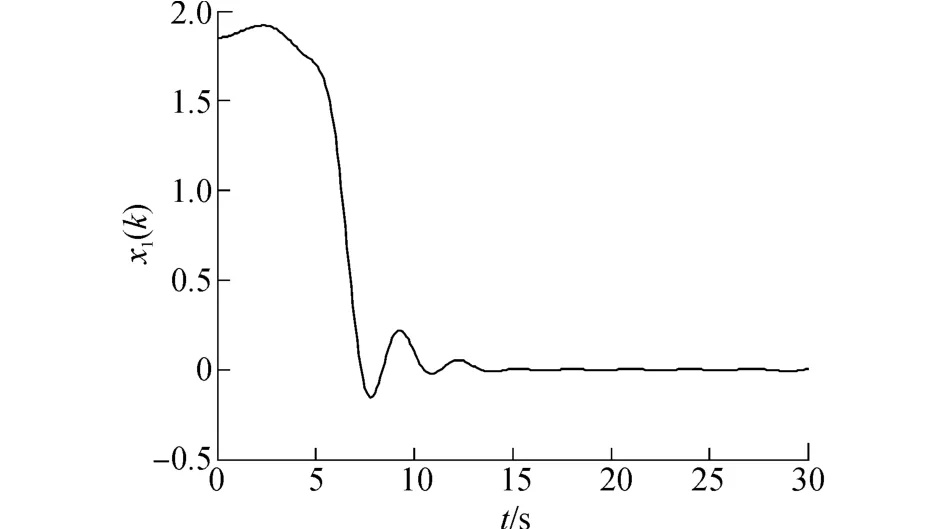
图1 状态x1(k)的时间响应曲线Fig．1 Time response of the state x1(k)

图3是控制器曲线图，可以看出在该控制器的作用下，系统是稳定的而且性能也很好。

4 结论

1）基于LMI技术及变量变换思想提出了一种min-max鲁棒预测控制算法，将时域为无限时的最小、最大优化问题转换为一类凸优化问题。解决了一类同时带有多重状态时滞、扰动和多面体不确定离散非线性系统的控制器设计问题。

2）算法通过利用所构造的改进的二次Lyapunov-Krasovskii泛函得到了所设计的控制器存在的新判据。应用LMI技术得到的鲁棒预测控制器，保证了系统的鲁棒稳定性，并分析了控制算法的可行性。

3）最后的仿真结果表明了该方法的有效可行。

［1］何德峰，丁宝苍，于树友．非线性系统模型预测控制若干基本特点与主题回顾［J］．控制理论与应用，2013，30（3）:273-287．HE Defeng，DING Baocang，YU Shuyou．Review of fundamental properties and topics of model predictive control for nonlinear systems［J］．Control theory＆applications，2013，30（3）:273-287．

［2］赵杰梅，胡忠辉，张利军．区间时滞相关离散非线性系统的鲁棒模型预测控制［J］．控制与决策，2015，30（1）: 59-64．ZHAO Jiemei，HU Zhonghui，ZHANG Lijun．Robust model predictive control for discrete-time nonlinear systems with delay-range-dependent［J］．Control and decision，2015，30（1）:59-64．

［3］俞华军．带有非线性扰动的不确定时滞系统鲁棒预测控制［J］．电子设计工程，2016，24（6）:190-193．YU Huajun．Robust predictive control of uncertain time-delay systems with nonlinear disturbance［J］．Electronic design engineering，2016，24（6）:190-193．

［4］CHEN Qiuxia，HE Defeng，YU Li．Input-to-state stability of min-max MPC scheme for nonlinear time-varying delay systems［J］．Asian journal of control，2012，14（2）:489-501．

［5］SHI Yujing，CHAI Tianyou，WANG Hong，et al．Delay-dependent robust model predictive control for time-delay systems with input constraints［C］／／Proceedings of the 2009 conference on American Control Conference．Piscataway，NJ，USA:ACM，2009:4880-4885．

［6］苏成利，赵家程，李平．一类具有非线性扰动的多重时滞不确定系统鲁棒预测控制［J］．自动化学报，2013，39（5）:644-649．SU Chengli，ZHAO Jiacheng，LI Ping．Robust predictive control for a class of multiple time delay uncertain systems with nonlinear disturbance［J］．Acta automatica sinica，2013，39（5）:644-649．

［7］LI Jianxiong，FANG Yiming，SHI Shengli．Robust MPC algorithm for discrete-time systems with time-varying delay and nonlinear perturbations［C］／／Proceedings of the 29th Chinese Control Conference．Beijing，China:China Automation Society Control Theory Specialized Committee，2010:3128-3133．

［8］ZHAO Juncheng，FANG Yiming，LI Jianxiong．Robust predictive control for a class of uncertain discrete system with multiple state delays［C］／／Proceedings of the 30th Chinese Control Conference．Yantai，China:IEEE，2011:3372-3376．

［9］俞立．鲁棒控制:线性矩阵不等式处理方法［M］．北京:清华大学出版社，2002．

［10］马新军，向少华，胥布工，等．带非线性扰动的不确定多时变时滞系统H∞鲁棒稳定性［J］．控制理论与应用，2006，23（4）:631-635．MA Xinjun，XIANG Shaohua，XU Bugong，et al．H-infinity robust stability for uncertain systems with multiple timevarying delays and nonlinear perturbations［J］．Control theory＆applications，2006，23（4）:631-635．

［11］KOTHARE M V，BALAKRISHNAN V，MORARI M．Robust constrained model predictive control using linear matrix inequalities［J］．Automatica，1996，32（10）:1361-1379．

Min-max robust predictive control for multi-state time-delay systems

ZHOU Weidong1，ZHENG Lan1，LIAO Chengyi2，CAI Jianan3
（1．College of Automation，Harbin Engineering University，Harbin 150001，China；2．Marine Design and Research Institute of China，Shanghai 200011，China；3．China Electronics Technology Group Corporation No．38 Research Institute，Hefei 230088，China）

For a class of convex polyhedron uncertain discrete nonlinear systems with disturbance and multi-state time delays，a min-max robust predictive control algorithm is proposed based on the predictive control theorem．Firstly，the model prediction control problem is described as a class of min-max problems for an infinite time-domain．Then，using liner matrix inequalitie（LMI）technology，the problem is transformed into a constraint problem and a state feedback controller designed．An improved Lyapunov-Krasovskii function is constructed using information provided，and the optimization problem is solved based on model predictive control theory．At the same time，the theorem and its proofs for the existence of the designed controller are also given．Thus，new evidence for the existence of a designed controller and a design method for the state feedback matrix were obtained．Based on this，a flowchart of the robust model predictive controller is given．Finally，a robust asymptotic stable theory of the closedloop system is given．Theoretical analysis and simulation demonstrate the feasibility of the controller and the robust asymptotic stability of the system．

nonlinear perturbation；multi-state time-delay；discrete nonlinear system；state feedback control；model predictive control；liner matrix inequalitie

10．11990／jheu．201510071

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．020．html

TP273

A

1006-7043（2016）12-1685-06

周卫东，郑兰，廖成毅，等．多重状态时滞系统的min-max鲁棒预测控制［J］．哈尔滨工程大学学报，2016，37（12）:1685-1690．

2015-10-28．

2016-09-28．

国家自然科学基金项目（61102107；61374208）．

周卫东（1966-），男，教授，博士生导师；

郑兰（1982-），女，博士研究生．

郑兰，E-mail:zhenglan000＠163．com．

ZHOU Weidong，ZHENG Lan，LIAO Chengyi，et al．Min-max robust predictive control for multi-state time-delay systems［J］．Journal of Harbin Engineering University，2016，37（12）:1685-1690．