弹/枪相互作用引起的运动步枪枪口振动分析*
刘国庆,徐诚
(南京理工大学机械工程学院,南京210094)
弹/枪相互作用引起的运动步枪枪口振动分析*
刘国庆,徐诚
(南京理工大学机械工程学院,南京210094)
为研究身管结构参数变化对运动步枪枪口振动的影响规律,采用非线性有限元方法建立了运动步枪弹/枪相互作用数值计算模型。借助压力测试系统对运动步枪进行了膛压测试试验;使用高速摄影设备实测了枪口在发射过程中竖直方向的振动规律,通过对比枪口实测数据与数值计算结果验证了模型的正确性。数值模型为研究参数变化对枪口振动的影响提供了理论基础,研究结果对工程实践具有一定实际意义。
运动步枪,弹/枪相互作用,高速摄影,枪口振动
0 引言
运动步枪是专为射击比赛而设计的特种步枪,其外形及发射原理与普通步枪基本相同,全铅弹头具有凸起的弹带结构,普遍采用单发射击结构,与普通步枪相比具有初速低、口径小、射程近等特点,但在相同射距内具有比狙击步枪更高的精度。运动步枪的设计理念与普通步枪恰恰相反,着重强调“枪适应人”的原则,具有良好的人机交互性能,因此,运动步枪通用性不如普通步枪,生产量少且价格昂贵。
目前国内外关于运动步枪的研究成果较少,并未形成系统的设计与分析方法,相关工作的开展多以借鉴其他身管武器的设计经验为主。文献[1]研究了火炮身管与炮弹间的相互作用关系,指出身管坡膛是归正弹丸及挤压弹带形成刻痕的重要结构,对身管武器的内弹道性能与射击精度有不可忽视的影响;文献[2]研究了参数变化对末制导炮弹发射过程的影响,指出弹带径向强制量起到密闭火药气体、定心与导引弹丸旋转的作用,强制量的增大有助于提高弹丸的出膛转速、转速比,但会加剧膛线的磨损而降低身管寿命;文献[3]研究了狙击步枪身管外形结构对枪口响应特性的影响,研究表明外形结构是提高身管固有频率增加身管稳定性的有效方法。
上述研究具有局限的适用性,而运动步枪的诸多性能参数与其他身管武器相差较大,不适于将上述研究结论直接应用于运动步枪,且相关性能参数并未进行系统的验证,因而迫切需要从理论与试验两方面对运动步枪开展研究。本文基于非线性有限元方法建立了运动步枪弹/枪相互作用数值计算模型,进行了膛压测试试验与高速摄影试验,从理论与试验两方面开展相关基础研究。
1 膛压测试试验
1.1 试验原理
内弹道时期,膛压是弹丸高速旋进与身管振动的能量来源,为准确获得所需数值计算载荷数据,本文以某型运动步枪为研究对象用电测法进行了膛压测试试验。电测法具有连续测量、精度高、动态特性好等优点,在弹道测试技术中应用较为普遍[4],电测压系统包括传感器、电荷放大器、数据处理与记录器及外设设备,试验流程框图如图1所示。

图1 膛压试验系统框图
选用Kistler 6215型压电式压力传感器与Kistler 5018A0001型电荷放大器测量膛压变化规律,该型传感器测压最大量程600MPa,灵敏度14900pC/MPa,为保证信号不失真同时减轻存储压力,设置NI数据采集系统采样频率100 KHz。
1.2 试验结果与分析
运动步枪膛压一致性高于普通步枪,电测压系统所测运动步枪典型性膛压变化规律如图2所示,运动步枪膛压变化规律与其他步枪有较大不同,总体特点为曲线尖锐、上升急促且下降缓慢平缓。
图2所示内弹道时期持续时间约2.8 ms,整个内弹道时期可分为3个比较显著的膛压变化阶段。第1阶段为膛压开始上升直至达到最大值,此阶段膛压上升较为急促,在0.21 ms时即达到最大值119.6 Mpa,上升时间与最大膛压值约为其他类型步枪的1/2。第2阶段为膛压下降阶段,最大膛压经0.81 ms下降至8 MPa,膛压经快速下降后逐渐趋于平缓。第3阶段为膛压准静止平衡状态,内弹道时期结束时仅下降了约2 MPa,弹丸出膛瞬间膛压值约为最大膛压值的1/20,此阶段膛压变化规律是运动步枪不同于其他身管武器的特点。
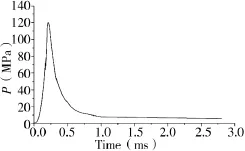
图2 运动步枪膛压曲线
2 枪口振动试验
2.1 试验原理
枪口振动是影响射击精度的重要根源之一,它的形成与发展受多种因素的影响[5]。枪口振动频率高、振幅小因而很难采用常规测试方法准确地捕捉,目前最直接有效的方法即使用高速摄影机拍摄枪口振动图片,经专用软件处理后得到枪口某一方向的振动位移,位移捕捉精度与高速摄影机拍摄频率有关。高速摄影系统由高速摄影机、外置光源与PC终端等组成,试验实物图如图3所示。发射系统由身管、夹持装置、发射装置与固定底座组成,试验实物如图4所示。

图3 枪口振动试验实物图

图4 运动步枪发射系统
高速摄影机拍摄频率为80 K,在运动步枪内弹道时期(2.8 ms)共可拍摄224幅枪口振动图片,能够较准确的记录枪口振动位移。
2.2 试验结果与分析
发射条件一致的情况下枪口振动呈现规律性、重复性的特点。高速摄影系统拍摄并处理所得具有典型意义的枪口振动位移(竖直方向)如图5所示。

图5 枪口中心位移曲线
图5中弹丸历时2.82 ms飞离枪口,枪口在0.77 ms时上扬至极大值,在2.3 ms时回落至极小值,出膛瞬间枪口处于上扬趋势;枪口在4.218 ms时上扬至第2个极大值,约为首次上扬位移的34倍,上扬之后枪口处于回落状态;枪口在5 ms内经历“上扬-回落-上扬-回落”的震荡,极值与周期均呈递增趋势。
枪口振动是时变动载荷激励下强迫响应的宏观表现,时变动载荷如弹丸高速运动、弹/枪作用力与火药压力激励身管产生应力波,枪口作为悬臂身管的自由端面使得应力波在此反射,反射波与入射波相互加强或减弱形成宏观振动;身管的强迫响应规律与动载荷变化及自身固有频率、夹持状态等因素有关。
3 弹/枪相互作用数值计算模型
3.1 有限元模型与材料参数
依据身管内膛尺寸与运动步枪弹外形参数建立其三维模型,使用有限元前处理软件划分网格,网格类型以六面体缩减积分单元(C3D8R)为主。身管坡膛对挤进过程影响较大,故对其进行网格加密处理,在轴向长度上共划分5个单元,其轴向密度为整体轴向密度的3倍;膛线深度尺寸远远小于身管外圆径向尺寸,为保证计算精度同时降低计算成本,将阳线与身管外圆分离单独划分网格,身管共划分368 352个网格,有助于精确获得内弹道过程中二者间的相互作用关系。
运动步枪弹丸为全铅材料,弹带在与身管接触、碰撞时受挤压形成刻痕,致使弹带处的应力集中现象较为严重,故在径向与轴向加大了弹带处的网格划分密度,加密后的网格尺寸为0.05 mm× 0.1 mm×0.1 mm,弹丸整体共划分258 140个网格,网格单元类型以C3D8R为主,弹丸有限元模型如图6所示。

图6 弹丸有限元模型
运动步枪身管夹持装置由固定底板与预紧轴套组成,夹持装置将身管有效的固定于枪架底座之上。由于夹持装置属于间接参与弹/枪间的相互作用且不是数值计算关注的重点,故对夹持装置进行了简化处理,夹持装置网格单元以C3D8R为主,其中预紧轴套共划分8 880个单元,固定底板共划分1 836个单元,运动步枪发射系统有限元模型如图7所示。全局坐标系Z轴为身管轴向,Y轴为竖直向上方向,X轴由右手定则确定。
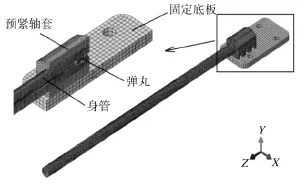
图7 运动步枪发射系统有限元模型
身管与夹持装置为高强度钢,弹丸材料为铅。相关基本力学性能参数如下:

表1 力学性能参数表
3.2 接触、边界条件与载荷的设置
采用面-面(Surface-to-Surface contact)接触类型定义弹带外表面与身管内膛之间、身管根部外表面与预紧轴套内表面之间的接触;弹丸受挤压产生刻痕并伴有材料流动现象,定义弹带前后端面与弹体外表面间的接触类型为自接触(Self-Contact);接触从初始步(Initial)即开始作用。接触控制算法采用惩罚函数法,其主要原理为当从面节点穿透主面时,求解器在节点上施加一个反作用力来将其拉回到主面之上,阻力的大小与穿透量成正比关系,从而能够有效避免从面节点对主面的穿透。
边界条件的施加保证了计算模型的约束状态与实际一致。预紧轴套下表面与固定底板上表面在发射过程中始终保持接触,适于采用绑定(Tie)约束限制两表面分离;固定底板通过螺栓固定于枪架底座,因而需要限制固定底板螺栓孔周边单元的所有自由度来模拟实际约束作用。发射过程中系统所受载荷为弹底膛压与重力,弹底膛压采用电测压试验数据,重力加速度取9.8 m/s2。
3.3 显隐式混合运算
弹丸发射前系统处于重力静平衡状态,主要表现为身管因自重而产生弯曲变形,该类静态问题适合使用隐式算法求解弯曲变形后的身管应力应变状态;弹丸发射过程历时短暂且伴随大的接触变形,适于使用显式算法求解身管瞬时状态及弹丸运动状态。本文结合两种算法的优点,将隐式计算所得身管应力应变状态导入显式求解器,重新设置约束状态、接触性质与初始场等计算初始条件,经混合运算获得因自重导致弯曲的身管与弹丸间的相互作用状态,充分考虑重力对发射过程的影响进而更真实的符合实际发射状态。
3.4 枪口振动数值计算结果与试验对比
由于重力的作用运动步枪身管在Y-Z面发生弯曲,枪口因此,下降至-0.248 63 mm,发射系统处于重力静平衡状态,以下垂后的枪口中心为零点,运用显式求解器求解该状态下弹丸发射过程,获得弹丸速度曲线及枪口振动位移曲线如图8、图9所示。

图8 弹丸速度曲线

图9 枪口振动位移曲线
该型运动步枪设计并经测速试验验证后的弹丸初速为320 m/s,图8中弹丸出膛速度317.6 m/s,数值计算结果与试验值误差约为0.75%。图9中数值计算结果显示枪口经0.66 ms上扬至极大值,所用时间比试验实测提前了14.3%,数值计算所得极大值比试验实测极大值小1.4%;枪口在1.78 ms下降至极小值,与试验实测值相比用时提前0.53 ms,极小值高10.6%。数值计算所得弹丸膛内运动时间为2.8 ms,与试验实测值相差0.7%。
数值计算所得枪口振动位移曲线总体表现为与试验曲线存在相位差,相位自极大值处逐步增加,在极小值处达到最大相位差后逐步减小。图8所示枪口振动位移数值计算曲线与试验曲线变化趋势基本一致,二者可近似看作变幅值、变周期的正弦三角曲线,曲线的极大值、极小值与出膛时刻值亦较为接近,验证了运动步枪弹/枪相互作用数值计算模型的正确性、有效性。由于数值计算模型在约束条件与试验有一定差别,因而导致了计算结果中产生第二小波峰,但总体趋势上与试验相符。
4 参数变化对枪口振动的影响
弹丸与身管间的相互作用是造成枪口振动的主因,振动幅度反映了弹丸膛内运动的剧烈程度。结构参数的变化改变弹/枪间的接触、碰撞规律与状态进而影响枪口振动,深入研究各个因素对枪口振动的影响规律有助于完善对运动步枪结构设计的认识。以上述建立的运动步枪弹/枪相互作用数值计算模型为理论基础,从身管坡膛锥度、阴线直径、刚度3个方面研究参数变化对枪口振动影响。
4.1 坡膛锥度变化对枪口振动的影响
弹丸挤进坡膛是一个极其复杂的非线性力学过程,主要表现为材料非线性、几何非线性与边界条件非线性[6],坡膛锥度对内弹道性能及身管振动具有明显影响。图10为身管坡膛锥度为3°、5°与7°时锥度变化对枪口振动的影响。
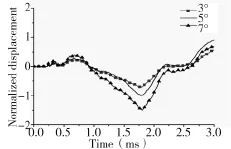
图10 锥度变化对枪口振动的影响
坡膛锥度为3°时枪口振动明显降低,其中枪口负方向最大位移约降低了28.7%,弹丸出膛时刻枪口位移降低了约49.8%,坡膛锥度为7°时负方向最大位移增大了49.7%,但出膛时刻的振动位移减小了约22.6%,表明较小的坡膛锥度有助于提高枪口的稳定。
4.2 内径变化对枪口振动的影响
身管线膛具有引导弹头旋转、密闭火药燃气和提高枪管寿命的作用[7],膛线阴阳线与弹丸为过盈配合,阴阳线直径的变化影响过盈量及弹/枪间的接触紧密性,进而改变弹丸膛内运动规律。分别建立了阴线直径为5.6 mm、5.63 mm与5.66 mm的身管有限元模型,当膛线深度一致时数值计算结果如图11所示。

图11 阴线直接变化对枪口振动的影响
图11中所示枪口振动幅度随阴线直径增大而增大。其中阴线直径为5.6 mm时枪口振动幅度分别降低了23.5%与20.5%,表明膛线深度不变时阴线直径减小有利于枪口稳定。阴线直径减小导致相对过盈量增大,因而身管与弹带间的接触更紧密,弹丸在膛内旋进时摆动角减小,二者间的作用力减弱则身管的振动较小。
4.3 身管刚度变化对枪口振动的影响
通常情况下身管刚度增加有助于降低身管振动,且能够减小因自重、温度引起的弯曲。分别建立了外径21 mm、23 mm与25 mm的身管有限元模型,其他结构参数保持不变时数值计算结果如图12所示。
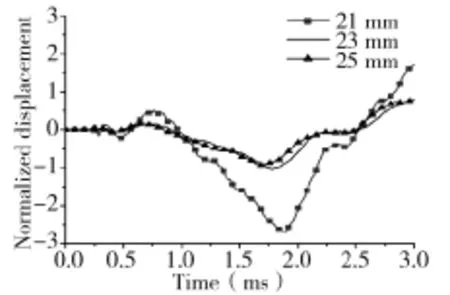
图12 刚度变化对枪口振动的影响
图12中所示,外径减小则枪口振动幅度明显增加,负方向最大位移与出膛时刻位移分别增大168%与37.3%,而当外径增大时并未明显提高枪管的稳定性,表明增加身管刚度并未达到降低身管振动的目的,但降低身管刚度则加剧枪管振动。
5 结论
为研究身管结构参数变化及弹重误差对运动步枪枪口振动的影响,基于非线性有限元方法建立了运动步枪弹/枪相互作用数值计算模型,考虑身管重力静平衡状态及弹丸挤进过程,深入研究了身管坡膛锥度、阴线直径、刚度对枪口振动的影响规律,分析计算结果得到如下结论:
(1)经高速摄影试验数据与数值计算结果的对比验证了弹/枪相互作用数值计算模型的正确性、有效性,本文建立的数值计算模型能够作为分析结构参数变化对枪口振动影响规律的理论工具。
(2)身管坡膛锥度减小有助于降低枪口振动同时导致弹丸初速下降,枪口振动降低49.8%,在允许的弹丸初速范围内可将坡膛锥度作为改善身管振动的设计优化参数。
(3)身管阴线直径减小导致枪口振动幅度降低20.5%,阴线直径偏大加剧枪口振动。因此,阴线直径减小有助于降低枪口振动。
(4)身管刚度降低显著加剧身管振动,振动幅度增加约168%,刚度增加并未明显提高身管的稳定性。
[1]孙河洋,马吉胜.坡膛结构变化对火炮内弹道性能影响的研究[J].兵工学报:2012,33(6):669-675.
[2]张振辉.末制导炮弹与火炮身管相互耦合机理及适配性技术[D].南京:南京理工大学,2013:89-91.
[3]齐心,申文杰,何亮.狙击步枪枪管动态特性分析[J].兵工自动化:2013,32(11):27-30.
[4]王昌明,高乃同.自动武器弹道学[M].北京:国防工业出版社,1990:150-152.
[5]康新中,吴三灵,马春茂.火炮系统动力学[M].北京:国防工业出版社,1999:29-40.
[6]葛建立.车载炮动态非线性有限元仿真研究[D].南京:南京理工大学,2007:27-29.
[7]王裕安,徐万和,薄玉成.自动武器构造[M].北京:兵器工业出版社,1991:2-4.
[8]赵定烽,朱江,丁劲.武器射程的一种新估算方法[J].火力与指挥控制,2010,35(12):53-55.
[9]王宇建,薛晋生.狙击步枪自动击发技术分析[J].火力与指挥控制,2015,40(2):182-184.
Analysis of Sporting Rifle Muzzle Response Characteristics Motivated by Interaction Between Bullet and Tube
LIU Guo-qing,XU Cheng
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
The numerical model of interaction between sporting rifle bullet and tube is established to study the vibration rule of muzzle which is influenced by the change of tube structure parameters. The bore pressure measurement experiment is conducted using pressure test system.The muzzle vibration rule at vertical direction during launching process is captured using high-speed photography equipment,and the correctness of model are verified by comparing measured data and numerical results.The establishment of numerical model provides theoretical basis for researching the effect of parameters on muzzle vibration and calculation results have certain significance to engineering practices.
sporting rifle,interaction between bullet and rifle,high-speed photography,muzzle vibration
TN95;TJ22
A
1002-0640(2016)12-0069-05
2015-11-02
2015-12-29
国防基础科研基金资助项目(A2620061288)
刘国庆(1988-),男,山东济宁人,在读博士生。研究方向:机械系统仿真与优化。

