一种求解线性对称变换方程的并行算法

邢 茁,吕全义

(西北工业大学 应用数学系,陕西 西安 710129)

一种求解线性对称变换方程的并行算法

邢 茁,吕全义

(西北工业大学 应用数学系,陕西 西安 710129)

研究求解线性对称变换方程的SYMMLQ并行算法.将求解线性方程组的SYMMLQ算法推广应用到求解线性对称变换方程,将并行过程中的两次全归约减少到一次,并对该算法进行改进,以提高并行性,减少计算时间.利用改进后的SYMMLQ算法在并行机上对Poisson方程与椭圆偏微分方程进行效果测试,并与未改进的SYMMLQ算法进行比较和分析.结果表明，改进的SYMMLQ算法的并行效率明显优于未改进的SYMMLQ算法.

线性对称变换方程;SYMMLQ算法;并行计算

0 引 言

线性变换方程包含最基本的线性方程组、线性矩阵方程,如Lyapunov矩阵方程,Sylvester矩阵方程等.这些方程(组)的求解问题广泛来源于控制理论[1]、图像恢复[2]、迁移理论中Riccati微分方程的数值解[3]、模型降阶[4-6]、线性系统的稳定性分析[7]等许多科学领域.

目前,求解大型线性变换方程通常采用迭代法,如ADI方法[8](Alternating Direction Implicit)及Krylov子空间法[9-13]等.ADI方法的不便之处在于确定最优参数;共轭梯度法[14](conjugate gradient method,简称CG法) 具有存储量小、适合并行计算等优点,但它仅适用于系数矩阵为对称正定的情形;变形共轭梯度法[15](modified conjugate gradient method,简称MCG法)的收敛速度与系数矩阵的条件数密切相关,条件数越小,收敛速度越快,因此MCG算法不适用于条件数较大的情形; SYMMLQ算法[16]适合求解系数矩阵为对称这一情形,其易于实现并行计算且收敛速度快.但是该算法的缺点是在并行实现过程中,需要两次全归约,由此引起的大规模全局通讯使得算法的可扩放性比较差[17-18].

1 SYMMLQ算法的推广

1.1 求解线性对称变换方程的SYMMLQ算法

文献[16]给出了求解对称情形下线性方程组的SYMMLQ算法,文中将该算法推广到求解线性对称变换方程,以拓宽其使用范围.

设线性变换T是n维欧式空间V上的对称变换,即∀X,Y∈V,有[T(X),Y]=[X,T(Y)].线性对称变换方程为

T(X)=F,

(1)

其中X∈V是未知的元素,F∈V是已知元素.

根据文献[12]的Lanczos过程,推广到线性对称变换方程，可得到如下关系式

考虑方程(1)的求解,令

X(k)=X(0)+(Q(1),Q(2),…,Q(k))f(k),

其中f(k)是k×1列向量.取f(k)使得R(k)=F-T(X(k))正交于Q(1),Q(2),…,Q(k),即

[Q(i),R(k)]=0(i=1,…,k).

(2)

因为

(3)

将式(3)左右两端分别与Q(i)(i=1,…,k)做内积,由式(2)和(3),可得

‖R(0)‖Fe1-Tkf(k)=0.

因为对称三对角矩阵Tk可能奇异,因而对它采用LQ分解,该过程类似于文献[12].于是,得到求解线性对称变换方程(1)的SYMMLQ算法(算法1):

(1) 任意给定初始元素X(0)∈V,置k:=1,计算

(2) 置k:=2,计算

(3) 计算ΔX(k-1)=X(k-1)-X(k-2),若‖ΔX(k-1)‖<ε停止计算;否则,计算

(4) 置k:=k+1,转(3).

1.2 SYMMLQ算法的收敛性分析

证明 由于

因为Q(k+1)正交于Q(1),Q(2),…,Q(k),所以

定理2 残量‖R(k)‖满足[R(k),R(j)]=0,其中j=1,2,…,k-1.

证明 由上述定理1的证明过程可知

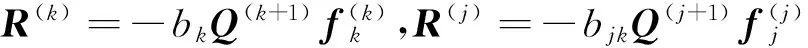
[Q(k+1),Q(j+1)]=0(j=1,2,…,k-1),

所以[R(k),R(j)]=0. 证毕.

定理3 设方程(1)相容,则对任意初始元素X(0)∈V,算法1至多需n步有R(n)=0,即至多需n步算法收敛(n为欧式空间的维数).

证明 n维欧式空间V中两两正交的非零元素至多为n个,又由定理2的结论可知对任意初始元素X(0)∈V所得到的残量R(0)与R(1),…,R(n-1),R(n)相互正交,因此算法1至多需n步有R(n)=0,即结论成立. 证毕.

2 SYMMLQ算法的并行实现

针对线性空间V=Rn×n上的对称变换T(X)=AX+XB,即方程(1)形式如下:

AX+XB=F.

(4)

其中A,B,F∈Rn×n,并且A=AT,B=BT.下面给出求解方程(4)的SYMMLQ算法的具体并行实现过程.

设处理机台数为p,p整除n,即n=pl,pi(i=1,2,…,p)表示第i台处理机.记

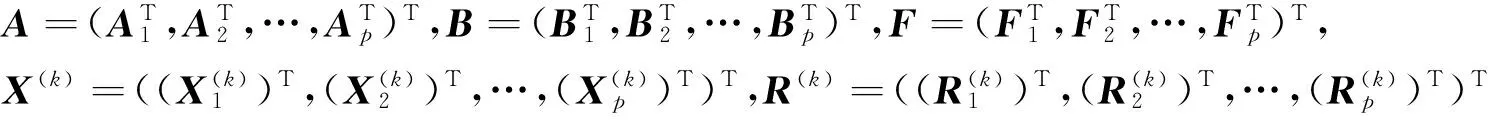
注 算法涉及到的所有矩阵乘法皆采用行行划分矩阵乘法的并行算法[17-18],文中所涉及的矩阵乘法并行计算不再描述.

2.1 未改进的SYMMLQ算法的并行实现

(2) 计算过程:

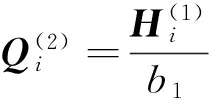
(3) 循环过程:

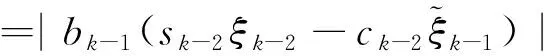
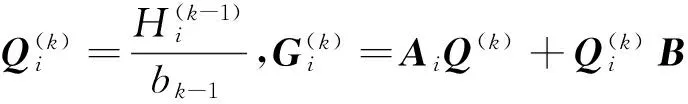
步骤4 在pi中,计算变量ξk=-(εkξk-2+δkξk-1)/rk以及

步骤5 置k:=k+1,返回步骤1.

2.2 改进的SYMMLQ算法的并行实现

在SYMMLQ算法的并行实现过程中,每迭代一次需要计算

ak=[T(Q(k)),Q(k)],bk=‖T(Q(k))-akQ(k)-bk-1Q(k-1)‖，

显然需要2次全归约.为了保证改进的SYMMLQ算法的结构稳定性,且基本不影响原算法的计算精度,在经过多次尝试后,对计算步骤进行重新安排,将上述计算步骤调整为如下形式:

这样,ak,ek的计算只需要1次全归约,从而达到减少通讯的目的.

调整步骤后,得到了改进的SYMMLQ算法.虽然这个过程需增加一些计算量,但相对很小.同时,改进的算法结构保持不变,所以编写程序代码时只需调整原算法相对应的循环过程步骤2即可,其余步骤保持不变.具体实现过程如下:

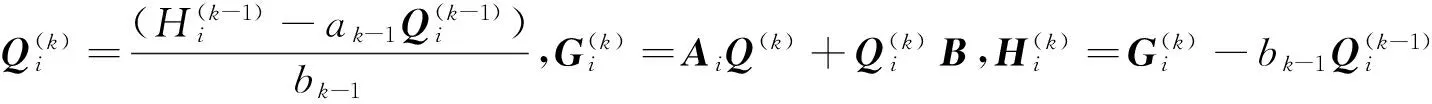
3 数值算例与结果分析

3.1 算例

在HPZ80工作站集群并行机上求解3个算例,分别采用SYMMLQ算法与本文提出的改进的SYMMLQ算法求解,并对计算结果进行比较.在迭代计算过程中,所有的初始矩阵X(0)为零矩阵,终止条件ε=10-6.

例1 Poisson方程第一边值问题

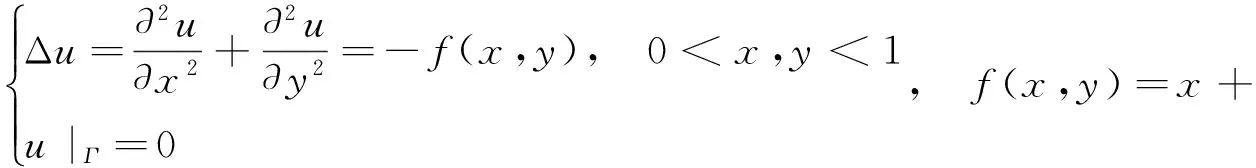
其中,Γ为单位正方形区域的边界,取步长h=1/1201.采用中心差分格式,可将本题转化为求解矩阵方程AX+XB=F的问题.设矩阵A=(aij)n×n,B=A,F=(fij)n×n,

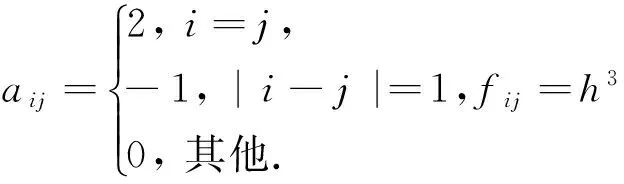
当n=1 200时,计算结果见表1.

表 1 例1计算结果

例2 在挡土墙的弹性力学分析中,由于其结构的形状和受力、约束情况具有一定的特点,所以将应力分量之间的关系近似表示为平衡偏微分方程，即

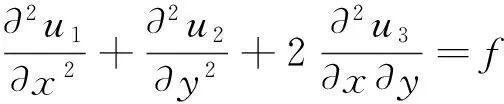
其中,假设正应力u1，u2与切应力u3平衡,即u1=u2=u3=u,并且f(x,y)=x+y,应力边界条件为u|Γ=0,Γ为受力边界.于是,平衡偏微分方程转化为

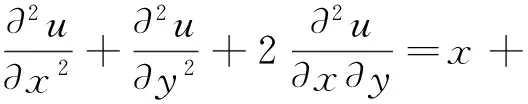
取步长h=1/1 001,采用中心差分格式以及一些近似处理,可将本题转化为求解Sylvester矩阵方程AX+XB=F的问题.设矩阵A=(aij)n×n,B=(bij)n×n,F=(fij)n×n,

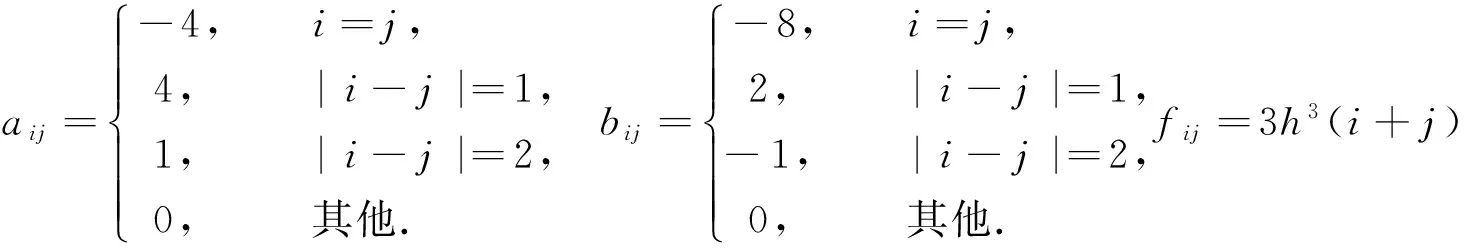
计算结果见表2.

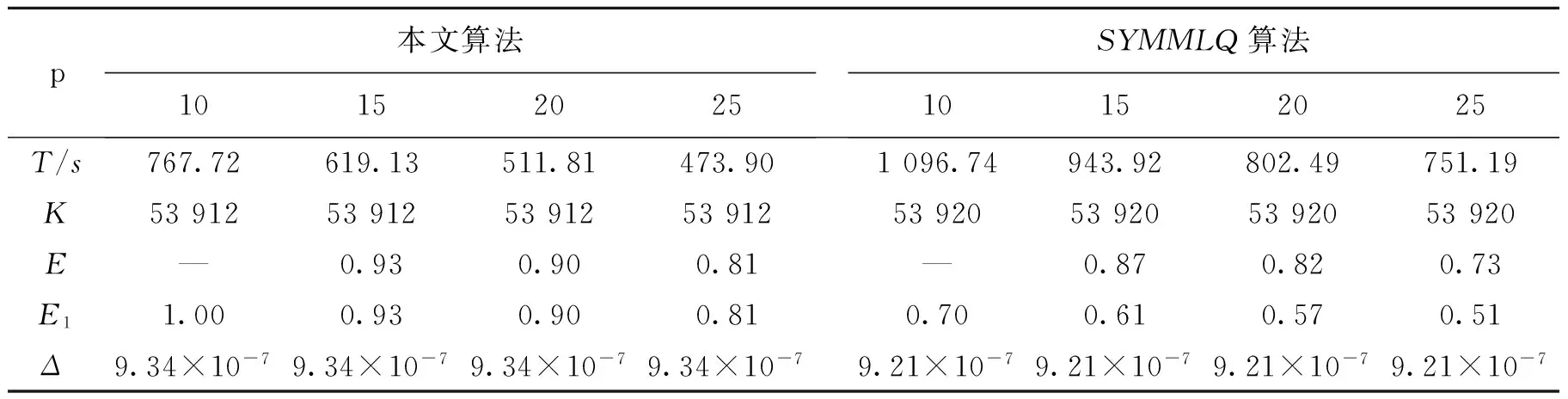
表 2 例2计算结果

例3 设矩阵A=(aij)n×n,B=(bij)n×n,其中

求解Sylvester矩阵方程AX+XB=F.在此取n=1 500,F为任意给定的矩阵.计算结果见表3.

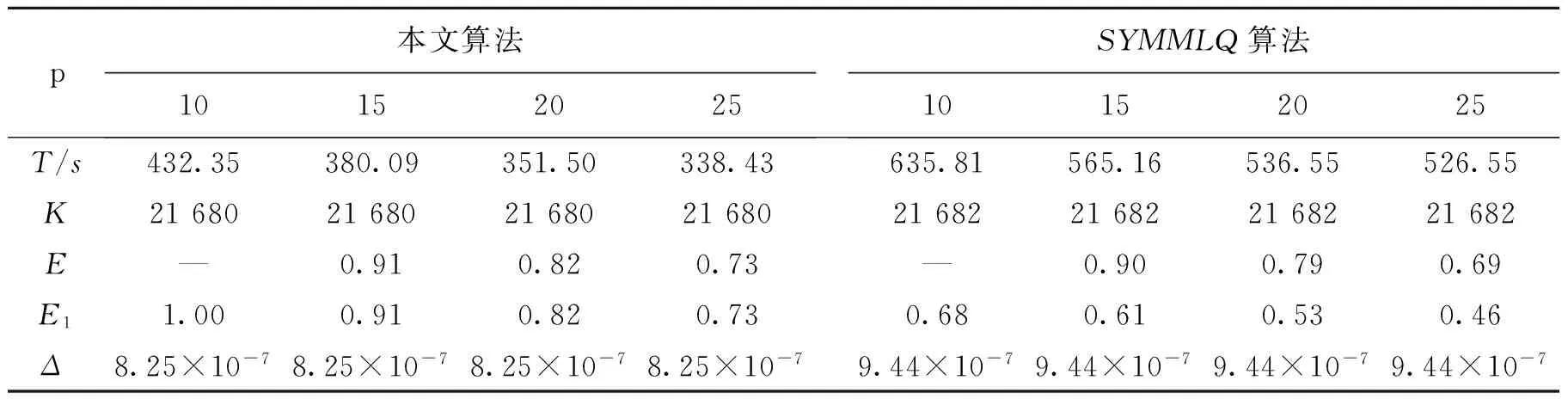
表 3 例3计算结果

表1～3中p表示处理机台数,T/s表示时间,K表示迭代次数,E表示相对并行效率,E1表示绝对并行效率,Δ表示误差‖R(k)‖.由于一台处理机的计算时间较长,因此采用多台处理机的计算时间,并且使用多台处理机中最小的计算时间作为基准来计算加速比和并行效率.

3.2 结果分析

(1) 改进的SYMMLQ算法比未改进的算法减少了并行计算时间,这是由于改进后的算法在循环迭代中减少了全归约的次数,从而缩短了全局通讯所引起的时间消耗.

(2) 改进的SYMMLQ算法的迭代次数与原SYMMLQ算法的迭代次数基本相同,说明改进的算法没有破坏原有SYMMLQ算法的结构与数值稳定性,而且由表中误差数据可以看出本文改进的算法对计算的精度影响不大.

(3) 表3数据表明当计算规模一定时,处理机增加到30台以上,并行效率会急剧下降,这是由于整体内积的计算与全收集而引起的大规模通讯使得消耗增加,进一步说明本文算法与原算法的可扩放性比较差,因此为保证较高的并行效率应采用适当数量的处理机.

致谢:感谢西北工业大学高性能计算研究与发展中心的大力支持!

[1] DATTA B.Numerical methods for linear control systems[M].Berlin:Elsevier Academic Press,2004.

[2] CALVETTI D,REICHEL L.Application of ADI iterative methods to the restoration of noisy images[J].Siam J Matrix Anal Appl,1996,17(1):165-186.

[3] ENRIGHT W H.Improving the efficiency of matrix operations in the numerical solution of stiff ordinary differential equations[J].ACM Trans Math Software,1978,4(2):127-136.

[4] ANTOULAS A C.Approximation of large-scale dynamical systems (Advances in design and control)[M].Philadelphia:Society of Industnal and Applied Mathematics,2005.

[5] BAUR U,BENNER P.Cross-gramian based model reduction for data-sparse systems[J].Electron Trans Numer Anal,2008,31(1):256-270.

[6] SORENSEN D,ANTOULAS A.The sylvester equation and approximate balanced reduction[J].Linear Algebra Appl,2002,351-352(2): 671-700.

[8] PEACEMAN D W,RACHFORD H H.The numerical solution of parabolic and elliptic differential equations[J].J Soc Ind Appl Math,1995,3(1): 28-41.

[9] GOLUB G H,LOAN C F.矩阵计算[M].北京:人民邮电出版社,2011.

GOLUB G H,LOAN C F.Matrix calculations[M].Beijing: Posts and Telecom Press,2011.

[10] 吴建平,王正华,李晓梅.稀疏线性方程组的高效求解与并行算法[M].长沙:湖南科学技术出版社,2004:269-273.

WU Jianping,WANG Zhenghua,LI Xiaomei.The efficient solution and parallel algorithm of spare linear equations[M].Changsha:Science and Technology Press of Hunan,2004:269-273.

[11] XIE Yajun,HUANG Na,MA Changfeng.Iterative method to solve the generalized coupled Sylvester-transpose linear matrix equations over reflexive or anti-reflexive matrix[J].Computers and Mathematics with Applications,2014,67(11):2071-2084.

[12] 蒋尔雄.矩阵计算[M].北京:科学出版社,2008.

JIANG Erxiong.Matrix calculations[M].Beijing:Science Press,2008.

[13] 李大明.数值线性代数[M].北京:清华大学出版社,2010.

LI Daming.Numerical linear algebra[M].Beijing:Tsinghua University Press,2008.

[14] 张凯院,徐仲.数值代数[M].2版.北京:科学出版社,2010.

ZHANG Kaiyuan,XU Zhong.Numerical algebra[M].2ed.Beijing:Scince Press,2010.

[15] 曹方颖,吕全义.预处理变形共轭梯度法并行求解矩阵的Moore-Penrose 逆[J].纺织高校基础科学学报,2013,26(1):137-142.

CAO Fangyin,LYU Quanyi.A parallel preconditioned modified conjugate gradient method of Moore-Penrose inverse of matrices[J].Basic Sciences Journal of Textile University,2013,26(1):137-142.

[16] PAIGN C C,SAUNDERS M A.Solution of sparse indefinite system of linear equations[J].Siam J Number Anal,1975,12(4):617-629.

[17] 李晓梅,吴建平.数值并行算法与软件[M].北京:科学出版社,2007.

LI Xiaomei,WU Jianping.Numerical parallel algorithm and software[M].Beijing:Science Press,2007.

[18] 李建江.并行计算机及编程基础[M].北京:清华大学出版社,2011.

LI Jianjiang.Parallel computers and programming base[M].Beijing:Tsinghua University Press,2011.

编辑、校对：师 琅

A parallel algorithm for solving equation of symmetrical linear transformation

XINGZhuo,LYUQuanyi

(Department of Applied Mathematics, Northwestern Polytechnical University,Xi′an 710129, China)

A parallel algorithm with SYMMLQ method for solving the equation of symmetrical linear transformation was studied.The SYMMLQ method for solving linear equations is extended to solve the equation of symmetrical linear transformation.The degree of reduce operator is decreased from twice to once in the parallel process so as to improve the parallelism of the algorithm and thus reduce the computing time.The Poisson equation and elliptic partial differential equation were tested with the proposed algorithm and the original one, and the results were compared and analyzed.It is shown that the proposed SYMMLQ algorithm is superior to the original SYMMLQ algorithm.

the equation of symmetrical linear transformation;SYMMLQ algorithm;parallel computation

1006-8341(2016)04-0508-07

10.13338/j.issn.1006-8341.2016.04.016

2016-06-11

陕西省自然科学基金资助项目(2009JM1008)

吕全义(1963—),女,辽宁省沈阳市人,西北工业大学副教授，研究方向为信息处理中的快速与并行算法.

E-mail:luquan@nwpu.edu.cn

邢茁,吕全义.一种求解线性对称变换方程的并行算法[J].纺织高校基础科学学报,2016,29(4)：508-514.

XING Zhuo,LYU Quanyi.A parallel algorithm for solving equation of symmetrical linear transformation[J].Basic Sciences Journal of Textile Universities,2016,29(4):508-514.

O 246

A